02预备知识——李沐《动手学深度学习》个人笔记

文章目录

思维导图
[2.1 数据操作（ndarray）](#2.1 数据操作（ndarray）)
- [2.1.1 创建](#2.1.1 创建)
- [2.1.2 改变形状](#2.1.2 改变形状)
- [2.1.3 运算](#2.1.3 运算)
- [2.1.4 索引与切片](#2.1.4 索引与切片)
- [2.1.5 原地赋值](#2.1.5 原地赋值)
- [2.1.6 类型转换](#2.1.6 类型转换)
[2.2 数据预处理（pandas）](#2.2 数据预处理（pandas）)
- [2.2.1 读取数据集](#2.2.1 读取数据集)
- [2.2.2 处理缺失值](#2.2.2 处理缺失值)
- [2.2.3 练习题解答](#2.2.3 练习题解答)
[2.3 线性代数](#2.3 线性代数)
- [2.3.1 标量](#2.3.1 标量)
- [2.3.2 向量](#2.3.2 向量)
- [2.3.3 矩阵](#2.3.3 矩阵)
- [2.3.4 张量](#2.3.4 张量)
- [2.3.5 范数](#2.3.5 范数)
- [2.3.6 练习题解答](#2.3.6 练习题解答)
[2.4 微积分](#2.4 微积分)
- [2.4.1 导数](#2.4.1 导数)
- [2.4.2 偏导数](#2.4.2 偏导数)
- [2.4.3 梯度](#2.4.3 梯度)
- [2.4.4 链式法则](#2.4.4 链式法则)
[2.5 自动微分](#2.5 自动微分)
[2.6 概率](#2.6 概率)
- [2.6.1 基本概念](#2.6.1 基本概念)
- [2.6.2 多个随机变量](#2.6.2 多个随机变量)
- [2.6.3 期望与方差](#2.6.3 期望与方差)
- [2.6.4 关键公式总结](#2.6.4 关键公式总结)
[2.7 查阅文档](#2.7 查阅文档)

思维导图

2.1 数据操作（ndarray）

2.1.1 创建

创建连续整数的行向量：x = torch.arange(12) # tensor([0, 1, 2, ..., 11])

全0张量：zeros_tensor = torch.zeros((2, 3, 4))

全1张量：ones_tensor = torch.ones((2, 3, 4))

随机正态分布：randn_tensor = torch.randn(3, 4) # 均值为0，标准差为1

从列表创建：custom_tensor = torch.tensor([[2, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])

2.1.2 改变形状

X = x.reshape(3, 4)

2.1.3 运算

（1）按元素运算 ：x+y x-y ...
（2）逻辑运算 ：X==Y，X>=Y，X<Y ...
（3）连接

沿行连接（增加行数）：cat0 = torch.cat((X, Y), dim=0)

沿列连接（增加列数）：cat1 = torch.cat((X, Y), dim=1)
（4）广播机制

2.1.4 索引与切片

（1）基本索引
X[-1]) # 最后一行: tensor([8., 9., 10., 11.])
print(X[1:3] # 第2到3行（不包括第3行）
（2）元素赋值 ：X[1, 2] = 9 # 修改单个元素
（3）区域赋值：X[0:2, :] = 12 # 前两行所有列赋值为12

2.1.5 原地赋值

Z[:] = X + Y

2.1.6 类型转换

（1）与numpy互转

NumPy数组 → 张量：B = torch.tensor(A)

张量 → NumPy数组：A = X.numpy()
（2）与Python标量转换

python 复制代码

a = torch.tensor([3.5])
print(a.item())     # 3.5 - 提取标量值
print(float(a))     # 3.5
print(int(a))       # 3

2.2 数据预处理（pandas）

2.2.1 读取数据集

data = pd.read_csv(data_file)

2.2.2 处理缺失值

（1）插值法

对于数值，用平均值替换： inputs = inputs.fillna(inputs.mean())

对于非数值，用独热编码：inputs = pd.get_dummies(inputs, dummy_na=True)
（2）删除法：data_dropna = data.dropna() # 删除包含任何缺失值的行

2.2.3 练习题解答

（1）创建包含更多行和列的原始数据集

python 复制代码

import pandas as pd
import numpy as np
import torch

# 创建100行5列的数据集
np.random.seed(42)
large_data = pd.DataFrame({
    'Rooms': np.random.choice([1, 2, 3, 4, np.nan], 100),
    'Bathrooms': np.random.choice([1, 1.5, 2, np.nan], 100),
    'Area': np.random.uniform(50, 200, 100),
    'Location': np.random.choice(['A', 'B', 'C', np.nan], 100),
    'Price': np.random.randint(100000, 500000, 100)
})

# 增加缺失值
for col in ['Rooms', 'Bathrooms', 'Location']:
    mask = np.random.random(100) < 0.3  # 30%缺失率
    large_data.loc[mask, col] = np.nan

print(f"数据集形状：{large_data.shape}")
print("前5行数据：")
print(large_data.head())

jupyter运行结果：

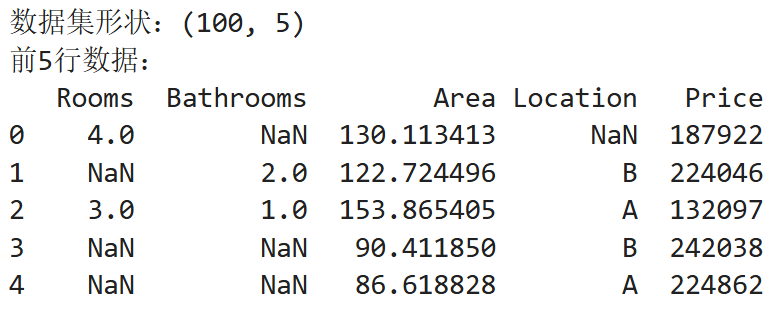
（2）删除缺失值最多的列

python 复制代码

# 计算每列缺失值比例
missing_ratio = large_data.isnull().sum() / len(large_data)
print("各列缺失比例：")
print(missing_ratio.sort_values(ascending=False))

# 删除缺失比例超过50%的列
threshold = 0.5
cols_to_drop = missing_ratio[missing_ratio > threshold].index

# 创建新的数据副本
if len(cols_to_drop) > 0:
    large_data_clean = large_data.drop(columns=cols_to_drop)
    print(f"\n删除了列：{list(cols_to_drop)}")
    print(f"新形状：{large_data_clean.shape}")
else:
    large_data_clean = large_data.copy()
    print("\n没有列被删除（所有列缺失比例 ≤ 50%）")
    print(f"原形状：{large_data_clean.shape}")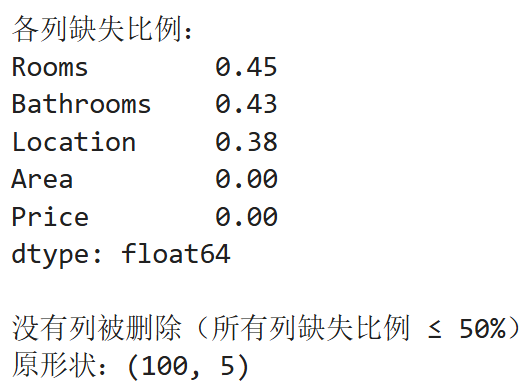

（3）将预处理后的数据集转换为张量格式

python 复制代码

# 检查large_data_clean是否存在
print(f"\n要处理的数据集：{'large_data_clean' in locals() or 'large_data_clean' in globals()}")

# 确保large_data_clean存在，如果不存在则使用原始数据
if 'large_data_clean' not in locals() and 'large_data_clean' not in globals():
    large_data_clean = large_data.copy()
    print("使用原始数据集作为large_data_clean")

# 分离特征和标签
features = large_data_clean.drop(columns=['Price'])
labels = large_data_clean['Price']

# 处理数值特征缺失值
numeric_cols = features.select_dtypes(include=[np.number]).columns
print(f"\n数值列：{list(numeric_cols)}")
features[numeric_cols] = features[numeric_cols].fillna(features[numeric_cols].mean())

# 处理类别特征
categorical_cols = features.select_dtypes(include=['object']).columns
print(f"类别列：{list(categorical_cols)}")

if len(categorical_cols) > 0:
    features = pd.get_dummies(features, columns=categorical_cols, dummy_na=True)
else:
    print("没有类别列需要处理")

# 转换为张量
X_tensor = torch.tensor(features.to_numpy(dtype=float))
y_tensor = torch.tensor(labels.to_numpy(dtype=float))

print(f"\n转换完成！")
print(f"特征张量形状：{X_tensor.shape}")
print(f"目标张量形状：{y_tensor.shape}")
print(f"特征类型：{X_tensor.dtype}")
print(f"目标类型：{y_tensor.dtype}")

2.3 线性代数

2.3.1 标量

仅包含一个数值的量

2.3.2 向量

定义：标量值组成的列表（一维数组）
操作
(1) 创建：x = torch.arange(4) # tensor([0, 1, 2, 3])
(2) 元素访问：x[3]
长度、维度和形状
- 长度/维度：len(x)
- 形状：x.shape

2.3.3 矩阵

定义：二维数组
操作
(1) 创建：A = torch.arange(20).reshape(5, 4) # 创建5×4矩阵
(2) 转置：A.T

2.3.4 张量

定义：具有任意数量轴的n维数组
标量：0阶张量
向量：1阶张量
矩阵：2阶张量
高阶张量：3阶及以上
创建：X = torch.arange(24).reshape(2, 3, 4) # 创建3阶张量（2×3×4）
运算
- (1) 按元素计算：A+B
  - Hadamard积 ：按元素乘法 A*B
- (2) 张量与标量计算：a + X
- (3) 求和
- (4) 平均值
- (5) 点积：torch.dot(x, y) 或者 torch.sum(x * y)
- (6) 矩阵-向量积：torch.mv(A, x)（A的列数必须等于x的长度）
- (7) 矩阵-矩阵乘法：torch.mm(A, B)

2.3.5 范数

定义：向量大小的度量
满足条件
- (1) f ( α x ) = ∣ α ∣ f ( x ) f(\alpha x) = |\alpha|f(x) f(αx)=∣α∣f(x)
- (2) f ( x + y ) ≤ f ( x ) + f ( y ) f(x + y) \leq f(x) + f(y) f(x+y)≤f(x)+f(y)（三角不等式）
- (3) f ( x ) ≥ 0 f(x) \geq 0 f(x)≥0
- (4) f ( x ) = 0 ⇔ x = 0 f(x) = 0 \Leftrightarrow x = 0 f(x)=0⇔x=0
Lp范数
- ∥ x ∥ 1 = ∑ i = 1 n ∣ x i ∣ \|x\|1 = \sum{i=1}^n |x_i| ∥x∥1=∑i=1n∣xi∣
Frobenius范数（矩阵范数）
- ∥ X ∥ F = ∑ i = 1 m ∑ j = 1 n x i j 2 \|X\|F = \sqrt{\sum{i=1}^m \sum_{j=1}^n x_{ij}^2} ∥X∥F=∑i=1m∑j=1nxij2

2.3.6 练习题解答

6.运行A/A.sum(axis=1)会发生什么？分析原因

python 复制代码

A = torch.arange(12, dtype=torch.float32).reshape(3, 4)
try:
    result = A / A.sum(axis=1)
    print(f"结果:\n{result}")
except RuntimeError as e:
    print(f"错误: {e}")
    print("原因：A.shape=(3,4)，A.sum(axis=1).shape=(3,)，形状不匹配无法广播")
    
# 正确做法：
result = A / A.sum(axis=1, keepdims=True)  # 形状(3,1)可广播到(3,4)
print(f"正确结果:\n{result}")

7.形状(2,3,4)的张量在轴0、1、2上求和的输出形状

python 复制代码

X = torch.arange(24).reshape(2, 3, 4)
print(f"原始形状: {X.shape}")
print(f"轴0求和形状: {X.sum(axis=0).shape}")  # (3, 4)
print(f"轴1求和形状: {X.sum(axis=1).shape}")  # (2, 4)
print(f"轴2求和形状: {X.sum(axis=2).shape}")  # (2, 3)
print(f"轴[0,1]求和形状: {X.sum(axis=[0, 1]).shape}")  # (4,)
print(f"轴[0,1,2]求和形状: {X.sum(axis=[0, 1, 2]).shape}")  # () 标量

8.linalg.norm函数对3个或更多轴的张量的输出

python 复制代码

# 创建不同维度的张量
tensor_1d = torch.tensor([1., 2., 3.])
tensor_2d = torch.tensor([[1., 2.], [3., 4.]])
tensor_3d = torch.ones(2, 3, 4)

print(f"1D张量范数: {torch.norm(tensor_1d)}")  # L2范数
print(f"2D张量范数: {torch.norm(tensor_2d)}")  # Frobenius范数
print(f"3D张量范数: {torch.norm(tensor_3d)}")  # 所有元素平方和的平方根

# 对于任意形状张量，torch.norm默认计算所有元素的L2范数
print(f"验证3D张量范数计算: sqrt(2*3*4) = {torch.sqrt(torch.tensor(24.0))}")

2.4 微积分

2.4.1 导数

几何意义：函数曲线在点 ( x , f ( x ) ) (x, f(x)) (x,f(x))处的切线斜率
符号： f ′ ( x ) 、 d f d x 、 d d x f ( x ) 、 D x f ( x ) f'(x)、\frac{df}{dx}、\frac{d}{dx}f(x)、D_x f(x) f′(x)、dxdf、dxdf(x)、Dxf(x)

2.4.2 偏导数

公式： ∂ y ∂ x i = lim ⁡ h → 0 f ( x 1 , ... , x i − 1 , x i + h , x i + 1 , ... , x n ) − f ( x 1 , ... , x i , ... , x n ) h \frac{\partial y}{\partial x_i} = \lim_{h \to 0} \frac{f(x_1, \dots, x_{i-1}, x_i + h, x_{i+1}, \dots, x_n) - f(x_1, \dots, x_i, \dots, x_n)}{h} ∂xi∂y=limh→0hf(x1,...,xi−1,xi+h,xi+1,...,xn)−f(x1,...,xi,...,xn)

2.4.3 梯度

公式： ∇ x f ( x ) = [ ∂ f ( x ) ∂ x 1 , ∂ f ( x ) ∂ x 2 , ... , ∂ f ( x ) ∂ x n ] ⊤ \nabla_{\mathbf{x}} f(\mathbf{x}) = \left[ \frac{\partial f(\mathbf{x})}{\partial x_1}, \frac{\partial f(\mathbf{x})}{\partial x_2}, \dots, \frac{\partial f(\mathbf{x})}{\partial x_n} \right]^\top ∇xf(x)=[∂x1∂f(x),∂x2∂f(x),...,∂xn∂f(x)]⊤
运算法则:
- 常数乘法： ∇ x [ c f ( x ) ] = c ∇ x f ( x ) \nabla_x [cf(x)] = c \nabla_x f(x) ∇x[cf(x)]=c∇xf(x)
- 加法： ∇ x [ f ( x ) + g ( x ) ] = ∇ x f ( x ) + ∇ x g ( x ) \nabla_x [f(x) + g(x)] = \nabla_x f(x) + \nabla_x g(x) ∇x[f(x)+g(x)]=∇xf(x)+∇xg(x)
- 线性函数： ∇ x ( a ⊤ x ) = a \nabla_x (a^\top x) = a ∇x(a⊤x)=a
- 二次型： ∇ x ( x ⊤ A x ) = ( A + A ⊤ ) x \nabla_x (x^\top A x) = (A + A^\top)x ∇x(x⊤Ax)=(A+A⊤)x

2.4.4 链式法则

公式： ∂ y ∂ x i = ∂ y ∂ u 1 ∂ u 1 ∂ x i + ∂ y ∂ u 2 ∂ u 2 ∂ x i + ⋯ + ∂ y ∂ u m ∂ u m ∂ x i \frac{\partial y}{\partial x_i} = \frac{\partial y}{\partial u_1} \frac{\partial u_1}{\partial x_i} + \frac{\partial y}{\partial u_2} \frac{\partial u_2}{\partial x_i} + \dots + \frac{\partial y}{\partial u_m} \frac{\partial u_m}{\partial x_i} ∂xi∂y=∂u1∂y∂xi∂u1+∂u2∂y∂xi∂u2+⋯+∂um∂y∂xi∂um

2.5 自动微分

核心概念：

（1）自动微分：框架自动计算导数的功能

（2）计算图：跟踪计算过程的数据结构

（3）反向传播：沿计算图反向传播梯度

计算流程：

python 复制代码

# 1. 启用梯度
x = torch.tensor(1.0, requires_grad=True)
# 2. 前向计算
y = x ** 2 + 3*x + 1
# 3. 反向传播
y.backward()
# 4. 获取梯度
print(x.grad)  # dy/dx = 2x + 3，在x=1时为5

关键方法：

方法	用途	示例代码
`requires_grad=True`	启用梯度	`x = torch.tensor(1.0, requires_grad=True)`
`backward()`	反向传播	`y.backward()`
`grad`	访问梯度	`x.grad`
`zero_()`	清零梯度	`x.grad.zero_()`
`detach()`	分离张量	`u = y.detach()`
`no_grad()`	禁用梯度	`with torch.no_grad():`

注意点：backword()输入为标量

python 复制代码

# 错误：向量直接反向传播
x = torch.tensor([1.0, 2.0], requires_grad=True)
y = x * 2  # y = [2.0, 4.0]
# y.backward() # ❌ 报错：grad can be implicitly created only for scalar outputs

# 正确：转换为标量
y.sum().backward()  # ✅ 计算sum(y)对x的梯度
# 或：y.mean().backward()
# 或：y.backward(torch.ones_like(y))

2.6 概率

2.6.1 基本概念

1.概率定义
概率：将事件映射到真实值的函数，表示事件发生的可能性
样本空间 S S S：所有可能结果的集合
事件：样本空间的子集

2.概率公理（科尔莫戈罗夫公理）

（1）非负性 ： P ( A ) ≥ 0 P(A) \geq 0 P(A)≥0

（2）规范性 ： P ( S ) = 1 P(S) = 1 P(S)=1

（3）可加性：互斥事件序列的概率等于各事件概率之和

3.随机变量
离散随机变量 ：取值可数（如掷骰子）
连续随机变量 ：取值不可数（如身高、体重）
表示： P ( X = a ) P(X=a) P(X=a) 表示随机变量 X X X 取值为 a a a 的概率

2.6.2 多个随机变量

1.联合概率 ： P ( A = a , B = b ) P(A=a, B=b) P(A=a,B=b) ，表示 A = a A=a A=a 和 B = b B=b B=b 同时发生的概率
2.条件概率 ： P ( B = b ∣ A = a ) = P ( A = a , B = b ) P ( A = a ) P(B=b \mid A=a) = \frac{P(A=a, B=b)}{P(A=a)} P(B=b∣A=a)=P(A=a)P(A=a,B=b)
3.贝叶斯定理 ： P ( A ∣ B ) = P ( B ∣ A ) P ( A ) P ( B ) P(A \mid B) = \frac{P(B \mid A)P(A)}{P(B)} P(A∣B)=P(B)P(B∣A)P(A)
4.边际化 ： P ( B ) = ∑ A P ( A , B ) P(B) = \sum_{A} P(A, B) P(B)=∑AP(A,B)

边际化结果的概率或分布称为边际概率（marginal probability）或边际分布
5.独立性
独立： A ⊥ B A \perp B A⊥B，满足 P ( A , B ) = P ( A ) P ( B ) P(A,B) = P(A)P(B) P(A,B)=P(A)P(B)
条件独立 ： A ⊥ B ∣ C A \perp B \mid C A⊥B∣C，满足 P ( A , B ∣ C ) = P ( A ∣ C ) P ( B ∣ C ) P(A,B \mid C) = P(A \mid C)P(B \mid C) P(A,B∣C)=P(A∣C)P(B∣C)

2.6.3 期望与方差

1.期望（均值）
随机变量期望 ： E [ X ] = ∑ x x P ( X = x ) E[X] = \sum_{x} x P(X=x) E[X]=∑xxP(X=x)
函数期望 ： E x ∼ P [ f ( x ) ] = ∑ x f ( x ) P ( x ) E_{x \sim P}[f(x)] = \sum_{x} f(x) P(x) Ex∼P[f(x)]=∑xf(x)P(x)

2.方差与标准差
方差： Var [ X ] = E [ ( X − E [ X ] ) 2 ] = E [ X 2 ] − ( E [ X ] ) 2 \text{Var}[X] = E[(X - E[X])^2] = E[X^2] - (E[X])^2 Var[X]=E[(X−E[X])2]=E[X2]−(E[X])2
标准差 ： σ X = Var [ X ] \sigma_X = \sqrt{\text{Var}[X]} σX=Var[X]
函数方差 ： Var [ f ( x ) ] = E [ ( f ( x ) − E [ f ( x ) ] ) 2 ] \text{Var}[f(x)] = E[(f(x) - E[f(x)])^2] Var[f(x)]=E[(f(x)−E[f(x)])2]

2.6.4 关键公式总结

概念	公式	说明
条件概率	P ( B ∣ A ) = P ( A , B ) P ( A ) P(B \mid A) = \frac{P(A,B)}{P(A)} P(B∣A)=P(A)P(A,B)	A发生时B的概率
贝叶斯定理	P ( A ∣ B ) = P ( B ∣ A ) P ( A ) P ( B ) P(A \mid B) = \frac{P(B \mid A)P(A)}{P(B)} P(A∣B)=P(B)P(B∣A)P(A)	逆概率计算
边际化	P ( B ) = ∑ A P ( A , B ) P(B) = \sum_A P(A,B) P(B)=∑AP(A,B)	消除变量A的影响
独立性	P ( A , B ) = P ( A ) P ( B ) P(A,B) = P(A)P(B) P(A,B)=P(A)P(B)	事件A、B相互独立
期望	E [ X ] = ∑ x x P ( X = x ) E[X] = \sum_x x P(X=x) E[X]=∑xxP(X=x)	随机变量平均值
方差	Var [ X ] = E [ X 2 ] − ( E [ X ] ) 2 \text{Var}[X] = E[X^2] - (E[X])^2 Var[X]=E[X2]−(E[X])2	离散程度度量

2.7 查阅文档

dir() - 列出模块所有属性和方法

help() - 查看详细文档说明

? (Jupyter) - 快速查看帮助

?? (Jupyter) - 查看源代码实现