从0开始学算法——第十三天（Rabin-Karp 算法）

写在开头的话

学习了昨天的KMP算法，今天让我们开始学习一个新的算法Rabin-Karp算法吧。

Rabin-Karp 算法是一种用于字符串匹配的算法，它利用哈希函数来实现快速匹配。也称作字符串哈希。它的核心思想是将模式字符串和文本字符串的子串转换为哈希值，从而在常数时间内进行比较。

第一节

知识点：

（1）Rabin-Karp 算法的动机（2）哈希函数的选择

Rabin-Karp 算法的动机

Rabin-Karp 算法是由 Michael O. Rabin 和 Richard M. Karp 在 1987 年提出的，它是用于字符串匹配的一种高效算法。为了更好地理解 Rabin-Karp 算法的动机，我们需要从字符串匹配问题的基本需求和常见挑战出发。他可以在O(1)的复杂度完成原本O(m)的字符串匹配。

字符串匹配问题

字符串匹配问题是在一个给定的文本字符串中查找某个模式字符串的所有出现位置。该问题在计算机科学中有广泛的应用，例如在文本编辑器中的查找功能、DNA 序列分析、网络安全中的模式检测等。

解决方案

Rabin-Karp 算法通过引入哈希函数和滚动哈希技术，提供了一种在实际应用中高效且易于实现的解决方案。

1. 利用哈希函数进行快速比较：

   • Rabin-Karp 算法的核心思想是使用哈希函数将字符串转换为整数值，从而可以在常数时间内比较字符串。通过计算模式字符串和文本子串的哈希值，我们可以快速判断两个字符串是否可能匹配。

2. 滚动哈希技术：

   • 直接计算每个子串的哈希值会导致时间复杂度过高。Rabin-Karp 算法采用了滚动哈希技术，通过利用前一个子串的哈希值来计算当前子串的哈希值，避免了重复计算，大大提高了效率。

3. 有效处理多模式匹配：

   • 在多模式匹配场景下，Rabin-Karp 算法可以同时计算多个模式的哈希值，然后在文本中查找匹配。这使得算法在处理多模式匹配问题时比传统方法更为高效。

4. 简化实现和应用广泛：

   • Rabin-Karp 算法的实现相对简单，并且易于扩展到其他领域。例如，除了字符串匹配，它还可以应用于文件比较、图像识别等领域。

具体动机示例

假设我们有一个长文本 text 和一个短模式 pattern，我们需要在 text 中查找所有 pattern 的出现位置。

• 传统方法：逐一比较 pattern 和 text 中的每一个子串，时间复杂度为O(n⋅m)。
• Rabin-Karp 方法：计算 pattern 的哈希值，并使用滚动哈希计算 text 中子串的哈希值，在常数时间内比较哈希值，时间复杂度平均为O(n+m)。

例如，给定 text = "abracadabra" 和 pattern = "abra"：

• 计算 pattern 的哈希值。
• 滚动计算 text 中每个长度为 4 的子串的哈希值。
• 比较哈希值，如果匹配，则进一步比较实际字符串，确认是否真正匹配。

通过这种方法，Rabin-Karp 算法在保证效率的同时，也降低了实现复杂度，并且可以处理多种实际应用场景。这就是 Rabin-Karp 算法的主要动机。

Rabin-Karp 算法中的哈希函数的选择

在 Rabin-Karp 算法中，哈希函数的选择是至关重要的。它直接影响算法的效率和碰撞概率。一个好的哈希函数应该在常数时间内计算，且能均匀地分布输入字符串的哈希值，从而最小化碰撞的概率。

哈希函数的要求

1. 高效性：哈希函数应当能够在常数时间内计算。
2. 均匀性：哈希函数应能均匀分布输入字符串的哈希值，以减少碰撞。
3. 可滚动性：哈希函数应当支持滚动计算，以便快速更新哈希值。

常用的哈希函数

在 Rabin-Karp 算法中，一个常用的哈希函数形式如下：

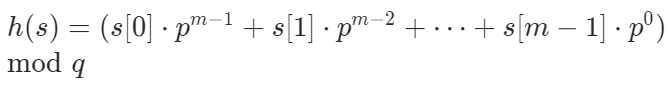
其中：

• s[i] 表示字符串的第 i 个字符的 ASCII 值。
• p 是一个大于字符串字符集大小的质数，用于计算哈希值。
• q 是一个较大的质数，用于取模，避免哈希值过大。

选择质数 p 和 q

• 质数 p ：

  • p 应该是一个大于字符串字符集大小（如 256）的质数。常用的值包括 31 或 101。

  • 选择质数可以减少哈希冲突，提高哈希值的均匀分布。

• 质数 q ： q 应该是一个较大的质数，用于取模操作，避免哈希值过大。

  • 典型的值可以是 1000000007 或其他大质数。
  • 取模操作确保哈希值在一个合理的范围内，有助于避免整数溢出。

滚动哈希计算

为了使哈希函数支持滚动计算，我们需要在常数时间内从前一个哈希值计算出下一个哈希值。

假设当前子串的哈希值为h(s×i)，下一子串为s×i+1，滚动哈希值的更新公式为：

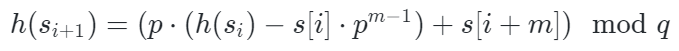
其中：

h(si​)是当前子串的哈希值。 s[i]是当前子串的第一个字符的 ASCII 值。 s[i+m]是下一个子串的最后一个字符的 ASCII 值。

示例

考虑一个简单的示例：

• 输入字符串为 "abc".
• 模式字符串为 "ab".
• 选择质数p=31和q=101.

1. 计算模式字符串 "ab" 的哈希值：

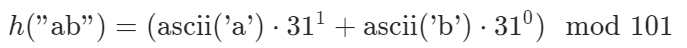
1. 计算文本字符串 "abc" 的前两个字符的哈希值：

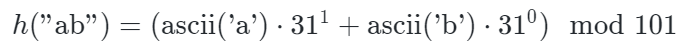
1. 使用滚动哈希更新下一个子串的哈希值：

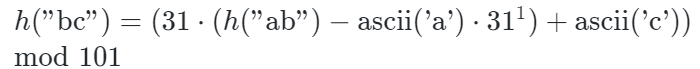
通过上述步骤，我们可以在常数时间内更新哈希值，从而高效地实现 Rabin-Karp 字符串匹配。

简单总结

选择一个合适的哈希函数是 Rabin-Karp 算法的关键。质数p和q的选择直接影响哈希冲突的概率和算法的效率。通过使用滚动哈希技术，我们可以在常数时间内更新哈希值，从而高效地进行字符串匹配。这些设计使得 Rabin-Karp 算法在处理大规模字符串匹配问题时具有显著的优势。

第二节

知识点：

（1）匹配过程与算法复杂度（2）哈希冲突处理（3）字符串哈希

字符串匹配

算法介绍

Rabin−Karp 算法是一种字符串匹配算法，用于在一个文本中查找一个模式的出现。它利用了哈希函数来快速比较模式和文本中的子串。该算法的主要思想是计算模式和文本中每个可能的子串的哈希值，并将其与模式的哈希值进行比较。如果哈希值匹配，那么可以进一步检查模式和子串是否确实匹配。

Rabin-Karp 算法的优点是在平均情况下具有较好的时间复杂度，特别是在模式较长的情况下。它的时间复杂度为 O(n+m)，其中 n 是文本长度，m 是模式长度。然而，它的缺点是在某些情况下可能会出现哈希冲突，导致需要进行额外的比较以确认匹配。

总的来说，Rabin−Karp​ 算法适用于需要在文本中查找多个不同模式的情况，而且它的实现相对简单，易于理解和使用。

在字符串匹配中，哈希函数可以用来将字符串映射到一个固定大小的哈希值，这个哈希值可以用来快速比较字符串是否相等。哈希函数的设计需要满足一些条件，例如：

• 确定性：相同的输入始终产生相同的哈希值。
• 均匀性：输入的微小改变会导致哈希值的显著变化，以尽量减少哈希冲突的可能性。

具体步骤

在 Rabin-Karp 算法中，使用哈希函数来计算模式和文本中每个可能的子串的哈希值。具体步骤如下：

• 计算模式的哈希值：使用哈希函数计算模式的哈希值。
• 计算文本中每个可能子串的哈希值：通过滑动窗口的方式，在文本中逐步计算每个可能的子串的哈希值。
• 比较哈希值：将模式的哈希值与文本中每个子串的哈希值进行比较。如果哈希值相等，再进一步检查模式和子串是否确实匹配。

通过哈希函数的计算，可以在常数时间内比较哈希值 ，从而实现快速的字符串匹配。然而，需要注意的是，哈希函数的选择和设计对算法的性能至关重要，不合适的哈希函数可能导致哈希冲突，降低算法的效率。

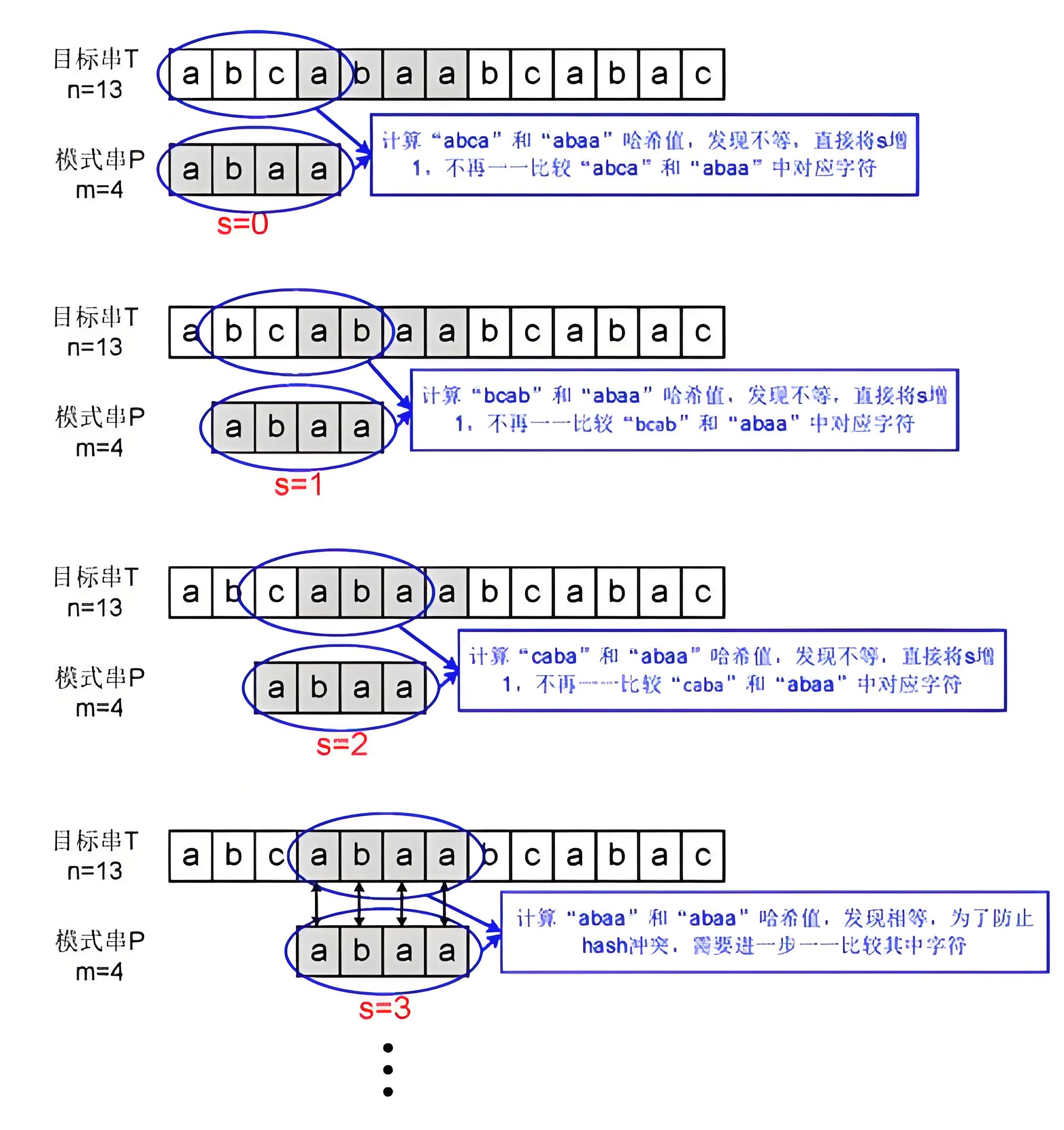
Rabin-Karp 字符串匹配过程

• 首先，通过哈希函数计算模式字符串的哈希值。这个哈希值通常是一个整数，表示模式字符串的特征值。
• 然后，在文本字符串中使用滑动窗口的方法，从左到右逐步计算每个长度与模式相同的子串的哈希值。滑动窗口的大小与模式字符串长度相同。
• 将模式的哈希值与文本中每个子串的哈希值进行比较。如果两个哈希值相等，则进行进一步的字符串比较，以确认是否真正匹配。如果哈希值不相等，则继续滑动窗口，计算下一个子串的哈希值。
• 当找到一个哈希值与模式哈希值相等的子串时，进行进一步的字符串比较，以确认是否真正匹配。如果匹配成功，则记录匹配的位置或者执行其他需要的操作。
• 在比较哈希值时，可能会出现哈希冲突，即不同的字符串具有相同的哈希值。在这种情况下，需要进行额外的比较以确认是否真正匹配。
• 重复以上步骤直到遍历完整个文本字符串，或者找到了所有的匹配位置。

图示

代码实现

C++代码实现

#include <iostream>
#include <string>
using namespace std;

// 定义一个简单的哈希函数，将字符串转换为整数
int hashFunc(const string& str, int len) {
    int hash = 0;
    for (int i = 0; i < len; ++i) {
        hash += str[i];
    }
    return hash;
}

// Rabin-Karp字符串匹配算法
void rabinKarp(const string& pattern, const string& text) {
    int patternLen = pattern.length();
    int textLen = text.length();

    // 计算模式字符串的哈希值
    int patternHash = hashFunc(pattern, patternLen);

    // 遍历文本中的每个可能子串
    for (int i = 0; i <= textLen - patternLen; ++i) {
        // 计算当前子串的哈希值
        int textHash = hashFunc(text.substr(i, patternLen), patternLen);

        // 比较哈希值，如果相等则进行进一步的字符串比较
        if (textHash == patternHash) {
            // 确认是否真正匹配
            if (text.substr(i, patternLen) == pattern) {
                // 如果匹配成功，则记录匹配的位置
                cout << "匹配成功在下标处 " << i << endl;
            }
        }
    }
}

int main() {
    string text = "ababcababcabcabc";
    string pattern = "abc";

    // 调用Rabin-Karp算法进行匹配
    rabinKarp(pattern, text);

    return 0;
}

Java代码实现

public class RabinKarp {
    // 定义一个简单的哈希函数，将字符串转换为整数
    private static int hashFunc(String str, int len) {
        int hash = 0;
        for (int i = 0; i < len; ++i) {
            hash += str.charAt(i);
        }
        return hash;
    }

    // Rabin-Karp字符串匹配算法
    private static void rabinKarp(String pattern, String text) {
        int patternLen = pattern.length();
        int textLen = text.length();

        // 计算模式字符串的哈希值
        int patternHash = hashFunc(pattern, patternLen);

        // 遍历文本中的每个可能子串
        for (int i = 0; i <= textLen - patternLen; ++i) {
            // 计算当前子串的哈希值
            int textHash = hashFunc(text.substring(i, i + patternLen), patternLen);

            // 比较哈希值，如果相等则进行进一步的字符串比较
            if (textHash == patternHash) {
                // 确认是否真正匹配
                if (text.substring(i, i + patternLen).equals(pattern)) {
                    // 如果匹配成功，则记录匹配的位置
                    System.out.println("Pattern found at index " + i);
                }
            }
        }
    }

    public static void main(String[] args) {
        String text = "ababcababcabcabc";
        String pattern = "abc";

        // 调用Rabin-Karp算法进行匹配
        rabinKarp(pattern, text);
    }
}

Python代码实现

def hash_func(string, length):
    """定义一个简单的哈希函数，将字符串转换为整数"""
    _hash = 0
    for i in range(length):
        _hash += ord(string[i])
    return _hash

def rabin_karp(pattern, text):
    """Rabin-Karp字符串匹配算法"""
    pattern_len = len(pattern)
    text_len = len(text)

    # 计算模式字符串的哈希值
    pattern_hash = hash_func(pattern, pattern_len)

    # 遍历文本中的每个可能子串
    for i in range(text_len - pattern_len + 1):
        # 计算当前子串的哈希值
        text_hash = hash_func(text[i:i+pattern_len], pattern_len)

        # 比较哈希值，如果相等则进行进一步的字符串比较
        if text_hash == pattern_hash:
            # 确认是否真正匹配
            if text[i:i+pattern_len] == pattern:
                # 如果匹配成功，则记录匹配的位置
                print("匹配成功在下标处 ", i)

text = "ababcababcabcabc"
pattern = "abc"

# 调用Rabin-Karp算法进行匹配
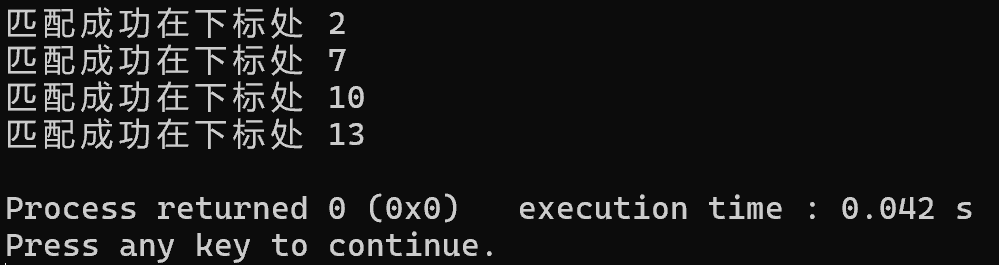
rabin_karp(pattern, text)

运行结果

哈希冲突

哈希冲突的原因

哈希冲突发生在哈希函数将不同的输入映射到相同的输出（哈希值）时。这种情况可能由于多种原因而发生：

• 哈希函数设计不当： 如果哈希函数没有很好地将输入均匀地分布到哈希表的不同位置，就容易导致哈希冲突。一个较差的哈希函数可能会导致大量的输入被映射到相同的哈希值，增加了发生冲突的可能性。

• 哈希表大小不足： 如果哈希表的大小不足以存储所有的输入元素，那么即使哈希函数设计良好，也会发生冲突。这种情况下，不同的输入将被强制映射到相同的哈希桶中，导致冲突。

• 输入数据的特性： 如果输入数据本身存在某种规律或者是有限的，那么即使哈希函数设计良好，也可能发生冲突。例如，当输入数据集合非常有限或者有规律时，可能会导致多个输入映射到相同的哈希值。

• 哈希函数碰撞： 即使哈希函数设计良好，也存在一定的可能性，不同的输入最终会映射到相同的哈希值。这种情况称为哈希函数的碰撞。虽然通常情况下，好的哈希函数会尽量减少碰撞的概率，但是无法完全避免。

在实际应用中，需要根据具体情况选择适当的哈希函数和哈希表大小，并且在设计哈希函数时考虑尽量减少冲突的可能性。

哈希冲突处理办法

在 Rabin−Karp 算法中，哈希冲突的处理通常不是必需的，因为该算法只是使用哈希值作为快速的筛选工具，真正的字符串比较是在哈希值相等的情况下进行的。但是，如果确实存在哈希冲突，可以采取以下一些方法来处理：

• 开放寻址法：在哈希冲突发生时，通过一个探测序列（如线性探测、二次探测等）在哈希表中寻找下一个可用的位置存储数据。
• 链地址法：使用链表或其他数据结构将具有相同哈希值的元素存储在同一个哈希桶中。
• 再哈希：当哈希冲突发生时，使用另一个哈希函数重新计算哈希值，然后将数据插入到新的位置。
• 哈希桶扩展：在哈希表装载因子过高时，扩展哈希表的大小，以减少冲突的概率。

在 Rabin−Karp 算法中，由于只是简单地比较哈希值，而不是将数据存储在哈希表中，因此通常不需要专门处理哈希冲突。

在这个代码中，我们定义了 rehash 函数，该函数用于在文本中滑动窗口时更新子串的哈希值。rehash 函数通过减去旧字符的值和添加新字符的值来更新哈希值，从而提高计算效率。这种滑动窗口的方式减少了计算所有字符的哈希值的开销，提高了算法的效率。

代码实现

C++代码实现

 // 处理哈希冲突的方法
    static int rehash(const string& text, int oldHash, int oldIndex, int patternLen) {
        // 从原哈希值中去除旧字符的值
        oldHash -= text[oldIndex];
        // 添加新字符的值
        oldHash += text[oldIndex + patternLen];
        return oldHash;
    }

Java代码实现

 // 处理哈希冲突的方法
    public static int rehash(String text, int oldHash, int oldIndex, int patternLen) {
        // 从原哈希值中去除旧字符的值
        oldHash -= text.charAt(oldIndex);
        // 添加新字符的值
        oldHash += text.charAt(oldIndex + patternLen);
        return oldHash;
    }

Python代码实现

   @staticmethod
    # 处理哈希冲突的方法
    def rehash(text: str, old_hash: int, old_index: int, pattern_len: int) -> int:
        # 从原哈希值中去除旧字符的值
        old_hash -= ord(text[old_index])
        # 添加新字符的值
        old_hash += ord(text[old_index + pattern_len])
        return old_hash

简单总结

在本节中，我们学习了匹配过程与算法复杂度和哈希冲突处理，利用已经匹配过的信息来避免不必要的比较，从而实现快速匹配。总的来说，Rabin-KarpRabin−Karp 算法利用了哈希函数的快速特性，以及滑动窗口的方法，实现了快速的字符串匹配。虽然在某些情况下可能会出现哈希冲突，但在平均情况下具有较好的时间复杂度。

第三节

知识点：

（1）滚动哈希的原理（2）Rabin-Karp算法的应用与优化

滚动哈希的原理

算法介绍

滚动哈希算法是一种用于字符串匹配的高效算法，其基本思想是通过哈希函数将字符串中的固定长度子串映射到一个哈希值，然后在比较字符串时，只需比较哈希值而不是比较整个子串。当移动匹配窗口时，我们只需通过减去最高位的字符的哈希值，然后加上新字符的哈希值，即可在常量时间内更新哈希值，从而实现快速的字符串匹配。

详细步骤

下面是滚动哈希算法的详细步骤：

• 选择哈希函数：首先，我们需要选择一个合适的哈希函数，它能够将字符串中的任意长度的子串映射到一个固定范围的哈希值。常见的哈希函数包括多项式哈希函数和基于素数的哈希函数。
• 计算初始哈希值：将哈希函数应用于文本串中的第一个固定长度子串，得到初始的哈希值。
• 匹配过程：从文本串的第一个位置开始，依次将长度为模式串长度的子串与模式串的哈希值进行比较。如果哈希值相等，则进行进一步的比较以确认是否匹配。
• 滑动窗口：在匹配过程中，不断向后移动匹配窗口。每次移动窗口时，我们只需要从当前哈希值中减去最高位的字符的哈希值，然后加上新字符的哈希值，以更新哈希值。这样就实现了在常量时间内更新哈希值的操作。
• 重复步骤3和步骤4：直到找到所有匹配的位置或者搜索完整个文本串。
• 处理哈希冲突：由于哈希函数是将一个无限的输入域映射到一个有限的输出域，因此可能会出现哈希冲突。为了应对这种情况，通常需要在哈希值相等时再进行一次实际的字符比较来确认匹配。

图示

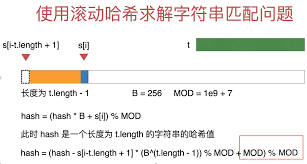
通过滚动哈希算法，我们可以在近似线性的时间复杂度内进行字符串匹配，从而实现了高效的字符串搜索和匹配操作。

Rabin-Karp算法是一种用于字符串匹配的经典算法，它利用了哈希函数的性质来在文本串中快速定位模式串的位置。与滚动哈希算法类似，Rabin-Karp算法也使用了哈希函数来将字符串映射到一个哈希值，然后在文本串中逐个比较子串的哈希值与模式串的哈希值。如果哈希值相等，则进行进一步的字符比较以确认匹配。

Rabin-Karp算法的应用与优化

Rabin-Karp算法详细步骤

下面是Rabin-Karp算法的详细步骤：

• 选择哈希函数：首先，我们需要选择一个哈希函数，它能够将字符串中的任意长度的子串映射到一个固定范围的哈希值。常见的哈希函数包括多项式哈希函数和基于素数的哈希函数。

• 计算模式串的哈希值：将哈希函数应用于模式串中的所有字符，得到模式串的哈希值。

• 计算文本串中每个长度为模式串的子串的哈希值：从文本串的第一个位置开始，依次计算每个长度为模式串的子串的哈希值。为了避免重复计算，我们可以利用滚动哈希的思想，在每次移动匹配窗口时只需更新哈希值。

• 比较哈希值：将文本串中每个子串的哈希值与模式串的哈希值进行比较。如果哈希值相等，则进行进一步的字符比较以确认匹配。

• 处理哈希冲突：由于哈希函数是将一个无限的输入域映射到一个有限的输出域，因此可能会出现哈希冲突。为了应对这种情况，通常需要在哈希值相等时再进行一次实际的字符比较来确认匹配。

• 重复步骤3和步骤4：直到找到所有匹配的位置或者搜索完整个文本串。

和普通的滚动哈希算法相比，Rabin-Karp算法通常使用大素数来减少冲突，并且会使用多哈希来降低误判率。

Rabin-Karp算法的时间复杂度取决于哈希函数的性能和哈希冲突的情况，但在平均情况下具有线性时间复杂度。由于它的简单性和高效性，Rabin-Karp算法在实际应用中被广泛使用于字符串匹配问题中。

代码实现

C++代码实现

#include <iostream>
#include <string>
using namespace std;

const int d = 256;

void search(const string& pat, const string& txt, int q) {
    int M = pat.length();
    int N = txt.length();
    int i, j;
    int p = 0; // 匹配串的哈希值
    int t = 0; // 模式串的哈希值
    int h = 1;

    // h的值为pow(d,M-1)%q
    for (i = 0; i < M - 1; i++)
        h = (h * d) % q;

    // 计算匹配串的哈希值以及模式串中第一个滑动窗口的哈希值
    for (i = 0; i < M; i++) {
        p = (d * p + pat[i]) % q;
        t = (d * t + txt[i]) % q;
    }

    // 滑动窗口过程
    for (i = 0; i <= N - M; i++) {

        // 检查当前模式串和匹配串中的滑动窗口中的值，如果哈希值能匹配上，就依次检查字符
        if (p == t) {
            for (j = 0; j < M; j++) {
                if (txt[i + j] != pat[j])
                    break;
            }

            // 如果p == t那么说明pat[0...M-1] = txt[i, i+1, ...i+M-1]
            if (j == M)
                cout << "Pattern found at index " << i << endl;
        }

        // 滑动窗口后计算哈希值
        if (i < N - M) {
            t = (d * (t - txt[i] * h) + txt[i + M]) % q;
            if (t < 0)
                t = (t + q);
        }
    }
}

int main() {
    string txt = "ABCAABCCBD";
    string pat = "ABC";
    int q = 101; // 一个质数
    search(pat, txt, q);
    return 0;
}

Java代码实现

public class Main 
{ 
    public final static int d = 256; 
    
    static void search(String pat, String txt, int q) 
    { 
        int M = pat.length(); 
        int N = txt.length(); 
        int i, j; 
        int p = 0; // 匹配串的哈希值
        int t = 0; // 模式串的哈希值
        int h = 1; 
    
        // h的值为pow(d,M-1)%q
        for (i = 0; i < M-1; i++) 
            h = (h*d)%q; 
    
        // 计算匹配串的哈希值以及模式串中第一个滑动窗口的哈希值 
        for (i = 0; i < M; i++) 
        { 
            p = (d*p + pat.charAt(i))%q; 
            t = (d*t + txt.charAt(i))%q; 
        } 
    
        // 滑动窗口过程 
        for (i = 0; i <= N - M; i++) 
        { 
    
            // 检查当前模式串和匹配串中的滑动窗口中的值，如果哈希值能匹配上，就依次检查字符 
            if ( p == t ) 
            { 
                for (j = 0; j < M; j++) 
                { 
                    if (txt.charAt(i+j) != pat.charAt(j)) 
                        break; 
                } 
    
                // 如果p == t那么说明pat[0...M-1] = txt[i, i+1, ...i+M-1]
                if (j == M) 
                    System.out.println("Pattern found at index " + i); 
            } 
    
             // 滑动窗口后计算哈希值 
            if ( i < N-M ) 
            { 
                t = (d*(t - txt.charAt(i)*h) + txt.charAt(i+M))%q; 
    
                if (t < 0) 
                    t = (t + q); 
            } 
        } 
    } 
    
    public static void main(String[] args) 
    { 
        String txt = "ABCAABCCBD"; 
        String pat = "ABC"; 
        int q = 101; // 一个质数 
        search(pat, txt, q); 
    } 
} 

Python代码实现

d = 256

def search(pat, txt, q):
    M = len(pat)
    N = len(txt)
    p = 0  # 匹配串的哈希值
    t = 0  # 模式串的哈希值
    h = 1

    # h的值为pow(d,M-1)%q
    for i in range(M - 1):
        h = (h * d) % q

    # 计算匹配串的哈希值以及模式串中第一个滑动窗口的哈希值
    for i in range(M):
        p = (d * p + ord(pat[i])) % q
        t = (d * t + ord(txt[i])) % q

    # 滑动窗口过程
    for i in range(N - M + 1):

        # 检查当前模式串和匹配串中的滑动窗口中的值，如果哈希值能匹配上，就依次检查字符
        if p == t:
            for j in range(M):
                if txt[i + j] != pat[j]:
                    break
            else:
                # 如果p == t那么说明pat[0...M-1] = txt[i, i+1, ...i+M-1]
                print("Pattern found at index", i)

        # 滑动窗口后计算哈希值
        if i < N - M:
            t = (d * (t - ord(txt[i]) * h) + ord(txt[i + M])) % q

            if t < 0:
                t = t + q

if __name__ == "__main__":
    txt = "ABCAABCCBD"
    pat = "ABC"
    q = 101  # 一个质数
    search(pat, txt, q)

运行结果

简单总结

本节主要学习了滚动哈希在字符串匹配中的作用，主要是Rabin-Karp的编写。