【算法基础篇】（三十二）动态规划之背包问题扩展：从多重到多维，解锁背包问题全场景

---

目录

​编辑

前言

一、背包扩展模型的核心逻辑：万变不离其宗

[二、多重背包：物品有使用次数限制的 "精准选择"](#二、多重背包：物品有使用次数限制的 “精准选择”)

[2.1 问题定义](#2.1 问题定义)

[2.2 与基础背包的核心区别](#2.2 与基础背包的核心区别)

[2.3 解法一：暴力枚举（基础版）](#2.3 解法一：暴力枚举（基础版）)

[2.3.1 思路分析](#2.3.1 思路分析)

[2.3.2 状态表示](#2.3.2 状态表示)

[2.3.3 状态转移方程](#2.3.3 状态转移方程)

[2.3.4 代码实现（暴力版）](#2.3.4 代码实现（暴力版）)

[2.3.5 复杂度分析](#2.3.5 复杂度分析)

[2.4 解法二：二进制优化（高效版）](#2.4 解法二：二进制优化（高效版）)

[2.4.1 核心优化思想](#2.4.1 核心优化思想)

[2.4.2 拆分步骤](#2.4.2 拆分步骤)

[2.4.3 代码实现（二进制优化版）](#2.4.3 代码实现（二进制优化版）)

[2.4.4 优化效果](#2.4.4 优化效果)

[2.5 实战案例：洛谷 P1077 摆花](#2.5 实战案例：洛谷 P1077 摆花)

题目描述

分析

状态表示

状态转移方程

代码实现

示例输入

示例输出

解释

[三、分组背包：每组只能选一个的 "互斥选择"](#三、分组背包：每组只能选一个的 “互斥选择”)

[3.1 问题定义](#3.1 问题定义)

[3.2 核心思路](#3.2 核心思路)

[3.3 状态表示与转移](#3.3 状态表示与转移)

状态表示

状态转移方程

[3.4 代码实现（基础版）](#3.4 代码实现（基础版）)

[3.5 实战案例：洛谷 P1757 通天之分组背包](#3.5 实战案例：洛谷 P1757 通天之分组背包)

题目描述

分析

代码实现

示例输入

示例输出

解释

[四、混合背包：多种规则并存的 "综合选择"](#四、混合背包：多种规则并存的 “综合选择”)

[4.1 问题定义](#4.1 问题定义)

[4.2 核心思路](#4.2 核心思路)

[4.3 代码实现（综合版）](#4.3 代码实现（综合版）)

计算过程

[4.4 实战案例：洛谷 P1833 樱花](#4.4 实战案例：洛谷 P1833 樱花)

题目描述

分析

代码实现

示例输入

示例输出

解释

[五、多维费用背包：多重约束下的 "权衡选择"](#五、多维费用背包：多重约束下的 “权衡选择”)

[5.1 问题定义](#5.1 问题定义)

[5.2 核心思路](#5.2 核心思路)

[5.3 代码实现（二维费用版）](#5.3 代码实现（二维费用版）)

[5.4 实战案例：洛谷 P1910 L 国的战斗之间谍](#5.4 实战案例：洛谷 P1910 L 国的战斗之间谍)

题目描述

分析

代码实现

示例输入

示例输出

解释

六、四大扩展模型对比总结

口诀：

七、常见误区与优化技巧

[7.1 常见误区](#7.1 常见误区)

[7.2 优化技巧](#7.2 优化技巧)

总结

---

前言

在动态规划的背包世界里，01 背包和完全背包是入门的 "敲门砖"，但真正的算法实战中，问题往往不会这么 "纯粹"------ 物品可能有使用次数限制、可能分成互斥的组、可能同时存在多种选择规则，甚至会有多重资源约束。这些复杂场景，正是多重背包、分组背包、混合背包和多维费用背包要解决的核心问题。

如果你已经掌握了基础背包的逻辑，恭喜你！接下来这篇文章，将带你 "升级打怪"，攻克背包问题的四大扩展模型。我们会从实际场景出发，拆解每种模型的核心痛点，推导状态转移方程，提供完整的 C++ 代码实现，还会分享优化技巧和避坑指南。

全文干货密集，适合有基础背包功底、想进阶提升的算法爱好者。建议收藏后慢慢研读，跟着代码敲一遍，彻底吃透背包扩展的精髓～下面就我们开始吧！

---

一、背包扩展模型的核心逻辑：万变不离其宗

在开始具体模型之前，我们先统一一个核心认知：所有背包扩展模型，本质都是基础背包的 "规则变种"。

它们的核心思想始终没变：

1. 状态表示 ：用dp[j]（或多维dp）存储 "使用不超过j资源时的最大价值"（或其他目标）；
2. 状态转移：通过 "选或不选"（或 "选几个 / 选哪组"）推导当前状态；
3. 核心目标：在资源约束下，最大化（或最小化）某个指标（价值、方案数等）。

变化的只是 "选择规则" 和 "约束条件"：

• 多重背包：物品有固定使用次数限制；
• 分组背包：物品分组成互斥集合，每组最多选一个；
• 混合背包：同时存在 01、完全、多重背包的物品；
• 多维费用背包：资源约束不止一个（如体积 + 重量、时间 + 金钱）。

掌握这个 "不变应万变" 的逻辑，再学习扩展模型就会事半功倍。接下来，我们逐个拆解每种模型。

二、多重背包：物品有使用次数限制的 "精准选择"

2.1 问题定义

多重背包的核心约束是：每种物品有固定的使用次数上限（既不能像 01 背包只能选 1 次，也不能像完全背包选无限次）。

举个生活化的例子：你去超市采购，背包容量 5L。货架上有 2 种物品：

• 物品 1：体积 2L，价值 10，最多 4 件；
• 物品 2：体积 4L，价值 100，最多 2 件。

请问如何选择，才能让背包内物品总价值最大？

这就是典型的多重背包问题 ------ 每个物品的选择次数被限制，需要在次数和容量双重约束下做最优决策。

2.2 与基础背包的核心区别

模型	选择次数约束	核心差异点
01 背包	最多 1 次	容量枚举从右到左，避免重复选择
完全背包	无限次	容量枚举从左到右，允许重复选择
多重背包	最多x[i]次	需额外枚举每个物品的使用次数

2.3 解法一：暴力枚举（基础版）

2.3.1 思路分析

多重背包的暴力解法，本质是**"将多重背包转化为 01 背包"** ------ 把每个有**x[i]次使用限制的物品，拆成x[i]**个完全相同的 01 背包物品，然后用 01 背包的解法求解。

比如物品 1 有 4 件，就拆成 4 个 "体积 2L、价值 10" 的独立物品，再按 01 背包的 "右到左" 枚举容量即可。

2.3.2 状态表示

dp[j]：使用不超过j的容量，能获得的最大价值。

2.3.3 状态转移方程

对于每个物品i，枚举其使用次数k（0 ≤ k ≤ x[i]且k*v[i] ≤ j）：

dp[j] = max(dp[j], dp[j - k*v[i]] + k*w[i])

• k=0：不选该物品，价值不变；
• k>0：选k件该物品，容量消耗k*v[i]，价值增加k*w[i]。

2.3.4 代码实现（暴力版）

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;

const int N = 110; // 物品数、容量最大值
int n, T; // n：物品种数，T：背包容量
int x[N], w[N], v[N]; // x：使用次数上限，w：价值，v：体积
int dp[N]; // dp[j]：容量j时的最大价值

int main() {
    // 示例输入：2种物品，容量8
    n = 2, T = 8;
    x[1] = 4, v[1] = 2, w[1] = 100; // 物品1：4件，体积2，价值100
    x[2] = 2, v[2] = 4, w[2] = 100; // 物品2：2件，体积4，价值100

    memset(dp, 0, sizeof dp);

    // 多重背包暴力解法：枚举物品、容量、使用次数
    for (int i = 1; i <= n; i++) {
        // 01背包逻辑：容量从右到左
        for (int j = T; j >= 0; j--) {
            // 枚举使用次数k：0到x[i]，且k*v[i] ≤ j
            for (int k = 1; k <= x[i] && k * v[i] <= j; k++) {
                dp[j] = max(dp[j], dp[j - k * v[i]] + k * w[i]);
            }
        }
    }

    cout << "多重背包暴力版最大价值：" << dp[T] << endl; // 输出400
    return 0;
}

2.3.5 复杂度分析

• 时间复杂度：O(n*T*max_x)，其中max_x是物品的最大使用次数；
• 空间复杂度：O(T)。

优点：逻辑简单，容易理解，适合**n、T、max_x都较小**的场景（如n≤100、T≤100、max_x≤20）。

缺点：效率较低，当**max_x**较大（如1e3）时，会超时。

2.4 解法二：二进制优化（高效版）

2.4.1 核心优化思想

暴力解法的问题在于 "重复枚举相同物品"，而二进制优化的核心是：用二进制数拆分使用次数x[i]，将x[i]个相同物品转化为log2(x[i])个 "超级物品" ，从而将时间复杂度从**O(n*T*max_x)降到O(n*T*log(max_x))**。

二进制拆分的原理：

• 任意整数x都可以拆成2^0, 2^1, 2^2, ..., 2^k, r的形式（其中r < 2^(k+1)）；
• 这些拆分后的数可以组合出[0, x]区间内的所有整数。

比如x=9，可以拆成1(2^0)、2(2^1)、4(2^2)、2(r=9-7=2)，这四个数能组合出 0-9 之间的所有整数（如 3=1+2，5=1+4，9=1+2+4+2）。

2.4.2 拆分步骤

1. 对于物品i，使用次数x[i]；
2. 初始化t=1（二进制基数）；
3. 当x[i] >= t时，拆出一个 "超级物品"：体积t*v[i]，价值t*w[i]，x[i] -= t，*t = 2；
4. 若x[i] > 0，拆出最后一个 "超级物品"：体积x[i]*v[i]，价值x[i]*w[i]；
5. 所有 "超级物品" 按 01 背包求解。

2.4.3 代码实现（二进制优化版）

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;

const int N = 110 * 5; // 拆分后最大物品数：110种物品，每种最多拆log2(20)=5次
const int M = 110; // 背包容量最大值
int n, T;
int w[N], v[N], pos; // pos：拆分后超级物品的下标
int dp[M];

int main() {
    n = 2, T = 8;
    // 原始物品：x[1]=4, v=2, w=100；x[2]=2, v=4, w=100
    int x[] = {0, 4, 2};
    int v_ori[] = {0, 2, 4};
    int w_ori[] = {0, 100, 100};

    // 二进制拆分
    for (int i = 1; i <= n; i++) {
        int cnt = x[i]; // 剩余使用次数
        int t = 1; // 二进制基数
        while (cnt >= t) {
            pos++;
            v[pos] = t * v_ori[i];
            w[pos] = t * w_ori[i];
            cnt -= t;
            t *= 2;
        }
        // 处理剩余部分
        if (cnt > 0) {
            pos++;
            v[pos] = cnt * v_ori[i];
            w[pos] = cnt * w_ori[i];
        }
    }

    // 01背包求解拆分后的超级物品
    memset(dp, 0, sizeof dp);
    for (int i = 1; i <= pos; i++) {
        for (int j = T; j >= v[i]; j--) {
            dp[j] = max(dp[j], dp[j - v[i]] + w[i]);
        }
    }

    cout << "多重背包二进制优化版最大价值：" << dp[T] << endl; // 输出400
    return 0;
}

2.4.4 优化效果

以x[i]=1e3为例：

• 暴力枚举：需要循环 1e3 次；
• 二进制拆分：log2(1e3)≈10，只需循环 10 次。

效率提升非常显著，是多重背包的主流优化方法。

2.5 实战案例：洛谷 P1077 摆花

题目链接：https://www.luogu.com.cn/problem/P1077

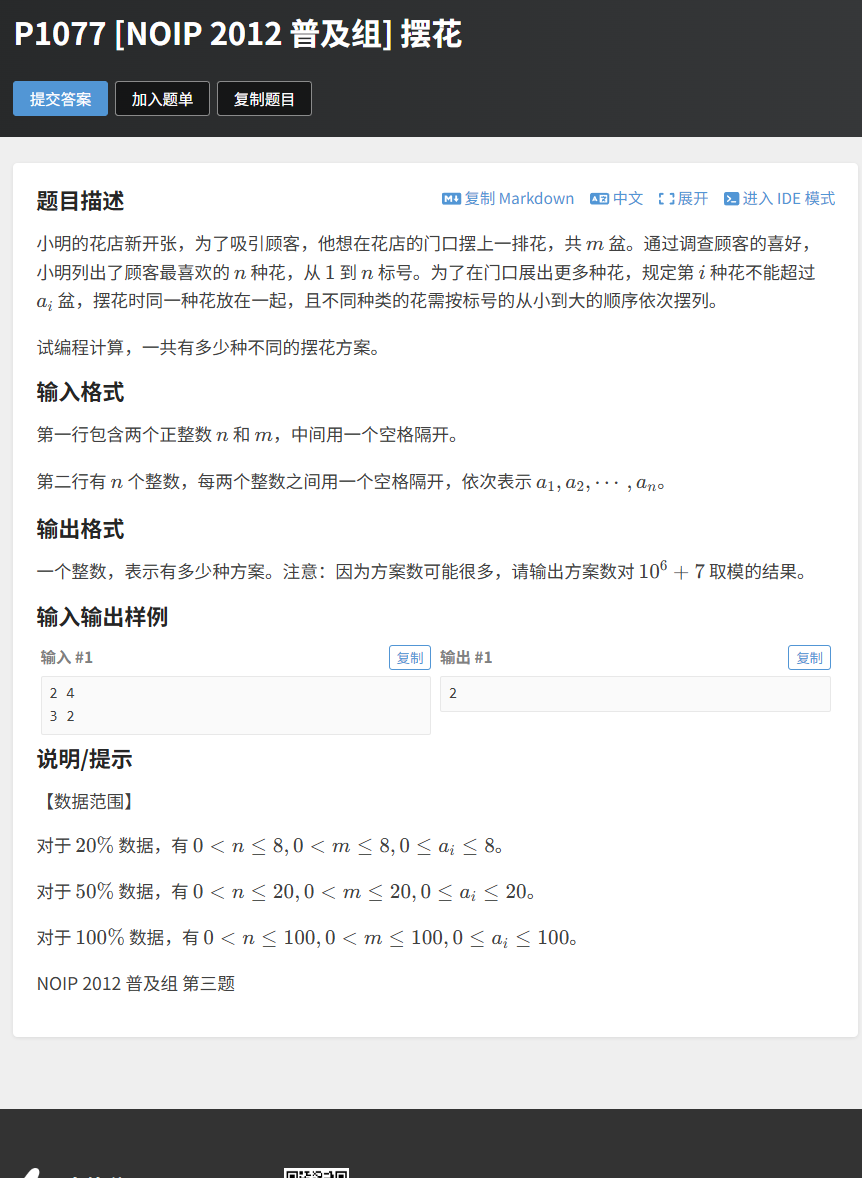
题目描述

小明的花店门口要摆m盆花，有n种花，第i种花最多摆a[i]盆。同一种花要放在一起，不同种花按标号顺序摆放。求有多少种不同的摆花方案（答案对1e6+7取模）。

分析

这是多重背包的 "方案数" 变种：

• 物品：n种花；
• 容量：m盆花；
• 约束：第i种花最多选a[i]盆；
• 目标：恰好选m盆的方案数。

状态表示

dp[j]：恰好摆j盆花的方案数。

状态转移方程

dp[j] = (dp[j] + dp[j - k]) % MOD

• k：第i种花选k盆（1 ≤ k ≤ min(a[i], j)）；
• 初始状态：dp[0] = 1（摆 0 盆花有 1 种方案：啥也不摆）。

代码实现

#include <iostream>
#include <cstring>
using namespace std;

const int N = 110;
const int MOD = 1e6 + 7;
int n, m;
int a[N];
int dp[N]; // dp[j]：恰好摆j盆的方案数

int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
    }

    memset(dp, 0, sizeof dp);
    dp[0] = 1; // 初始状态

    for (int i = 1; i <= n; i++) {
        // 多重背包方案数：容量从右到左（避免重复计数）
        for (int j = m; j >= 0; j--) {
            // 枚举选k盆第i种花
            for (int k = 1; k <= a[i] && k <= j; k++) {
                dp[j] = (dp[j] + dp[j - k]) % MOD;
            }
        }
    }

    cout << dp[m] << endl;
    return 0;
}

示例输入

2 4
3 2

示例输出

2

解释

• 方案 1：第 1 种花 3 盆 + 第 2 种花 1 盆（3+1=4）；
• 方案 2：第 1 种花 2 盆 + 第 2 种花 2 盆（2+2=4）。

三、分组背包：每组只能选一个的 "互斥选择"

3.1 问题定义

分组背包的核心约束是：物品被分成若干组，每组中的物品相互互斥，最多选择一个。

生活化场景：你要参加旅行，背包容量 5L。物品分成 3 组：

• 组 1（交通工具）：自行车（体积 2L，价值 10）、电动车（体积 3L，价值 15）；
• 组 2（食物）：面包（体积 1L，价值 5）、巧克力（体积 2L，价值 8）；
• 组 3（工具）：帐篷（体积 4L，价值 20）、睡袋（体积 3L，价值 18）。

每组最多选一个物品，如何选择能让总价值最大？

这就是分组背包的核心场景 ------ 每组内部是 "选或不选" ，但只能选一个，组与组之间是**"独立选择"**。

3.2 核心思路

分组背包的解法可以概括为 "组内 01 背包，组间顺序枚举"：

1. 枚举每组；
2. 对于每组，按 01 背包的 "右到左" 枚举容量（避免同一组选多个物品）；
3. 对于每组内的每个物品，更新状态。

3.3 状态表示与转移

状态表示

dp[j]：使用不超过j的容量，选择若干组物品（每组最多一个）的最大价值。

状态转移方程

对于第i组的第k个物品（体积v，价值w）：

dp[j] = max(dp[j], dp[j - v] + w)

• 前提：j >= v；
• 核心：同一组内的物品竞争同一容量，保证每组最多选一个。

3.4 代码实现（基础版）

#include <iostream>
#include <algorithm>
#include <vector>
#include <cstring>
using namespace std;

typedef pair<int, int> PII; // 存储物品的体积和价值
const int N = 1010; // 容量最大值
int m, n; // m：背包容量，n：物品总数
vector<PII> groups[N]; // groups[i]：第i组的所有物品
int dp[N];

int main() {
    // 示例输入：容量45，3个物品，分2组
    m = 45, n = 3;
    groups[1].push_back({10, 10}); // 组1：体积10，价值10
    groups[1].push_back({10, 5});  // 组1：体积10，价值5
    groups[2].push_back({50, 400});// 组2：体积50，价值400（超容量，无法选）

    memset(dp, 0, sizeof dp);

    // 分组背包：枚举每组
    for (int i = 1; i <= 2; i++) {
        // 组内01背包：容量从右到左
        for (int j = m; j >= 0; j--) {
            // 枚举组内每个物品
            for (auto& item : groups[i]) {
                int v = item.first, w = item.second;
                if (j >= v) {
                    dp[j] = max(dp[j], dp[j - v] + w);
                }
            }
        }
    }

    cout << "分组背包最大价值：" << dp[m] << endl; // 输出10
    return 0;
}

3.5 实战案例：洛谷 P1757 通天之分组背包

题目链接：https://www.luogu.com.cn/problem/P1757

题目描述

有n件物品，总重量m。每件物品有重量a[i]、价值b[i]、所属组c[i]。每组内的物品相互冲突，最多选一个。求最大利用价值。

分析

标准分组背包问题，只需将物品按组归类，然后按分组背包模板求解。

代码实现

#include <iostream>
#include <vector>
#include <algorithm>
#include <cstring>
using namespace std;

typedef pair<int, int> PII;
const int N = 1010;
int m, n; // m：总重量，n：物品数
vector<PII> g[N]; // g[i]：第i组的物品（重量，价值）
int dp[N];
int max_group; // 最大组号

int main() {
    cin >> m >> n;
    for (int i = 1; i <= n; i++) {
        int a, b, c;
        cin >> a >> b >> c;
        g[c].push_back({a, b});
        max_group = max(max_group, c);
    }

    memset(dp, 0, sizeof dp);

    // 枚举每组
    for (int i = 1; i <= max_group; i++) {
        // 组内01背包：右到左枚举重量
        for (int j = m; j >= 0; j--) {
            for (auto& item : g[i]) {
                int w = item.first, val = item.second;
                if (j >= w) {
                    dp[j] = max(dp[j], dp[j - w] + val);
                }
            }
        }
    }

    cout << dp[m] << endl;
    return 0;
}

示例输入

45 3
10 10 1
10 5 1
50 400 2

示例输出

10

解释

• 组 1 的两个物品体积都是 10，价值 10 和 5，选价值 10 的；
• 组 2 的物品体积 50>45，无法选；
• 总价值 10。

四、混合背包：多种规则并存的 "综合选择"

4.1 问题定义

混合背包的核心特点是：同一问题中，同时存在 01 背包、完全背包、多重背包的物品。

生活化场景：你去商场购物，背包容量 10L：

• 01 背包物品：限量款衣服（体积 3L，价值 20，仅 1 件）；
• 完全背包物品：矿泉水（体积 1L，价值 2，无限供应）；
• 多重背包物品：纸巾（体积 2L，价值 5，最多 3 包）。

如何选择能让总价值最大？

混合背包的解法，本质是**"分类处理"**------ 对不同类型的物品，采用对应的背包求解逻辑。

4.2 核心思路

1. 遍历每个物品；
2. 判断物品类型（01、完全、多重）；
3. 对不同类型的物品，采用对应的容量枚举顺序和状态转移方式：

• 01 背包：容量从右到左；
• 完全背包：容量从左到右；
• 多重背包：二进制拆分后按 01 背包处理，或暴力枚举次数。

4.3 代码实现（综合版）

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;

const int N = 1010; // 容量最大值
int V; // 背包容量
int dp[N];

// 处理01背包物品
void zero_one_pack(int v, int w) {
    for (int j = V; j >= v; j--) {
        dp[j] = max(dp[j], dp[j - v] + w);
    }
}

// 处理完全背包物品
void complete_pack(int v, int w) {
    for (int j = v; j <= V; j++) {
        dp[j] = max(dp[j], dp[j - v] + w);
    }
}

// 处理多重背包物品（二进制优化）
void multiple_pack(int v, int w, int x) {
    int t = 1;
    while (x >= t) {
        zero_one_pack(t * v, t * w);
        x -= t;
        t *= 2;
    }
    if (x > 0) {
        zero_one_pack(x * v, x * w);
    }
}

int main() {
    V = 10; // 背包容量10
    memset(dp, 0, sizeof dp);

    // 01背包物品：衣服（v=3, w=20, x=1）
    zero_one_pack(3, 20);

    // 完全背包物品：矿泉水（v=1, w=2）
    complete_pack(1, 2);

    // 多重背包物品：纸巾（v=2, w=5, x=3）
    multiple_pack(2, 5, 3);

    cout << "混合背包最大价值：" << dp[V] << endl; // 输出39
    return 0;
}

计算过程

• 衣服（3L，20）+ 矿泉水（5L，10）+ 纸巾（2L，5）：总容量 3+5+2=10，总价值 20+10+5=35；
• 优化选择：衣服（3L，20）+ 纸巾 3 包（6L，15）+ 矿泉水 1 瓶（1L，2）：总价值 20+15+2=37？
• 正确最优解：矿泉水 10 瓶（10L，20）？不，衣服 + 纸巾 3 包 + 矿泉水 1 瓶：3+6+1=10，价值 20+15+2=37；
• 实际最优解：衣服（20）+ 纸巾 3 包（15）+ 矿泉水 1 瓶（2）=37？或矿泉水 10 瓶（20）？显然前者更优。

4.4 实战案例：洛谷 P1833 樱花

题目链接：https://www.luogu.com.cn/problem/P1833

题目描述

爱与愁大神有n棵樱花树，每棵树有观赏时间T[i]、美学值C[i]、观赏次数限制P[i]（P[i]=0表示无限次，P[i]>0表示最多P[i]次）。他从T_s到T_e有m分钟时间，求最大美学值。

分析

标准混合背包问题：

• P[i]=0：完全背包；
• P[i]=1：01 背包；
• P[i]>1：多重背包。

代码实现

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

const int N = 1e4 + 10;
const int M = 1010; // 时间最大值（≤1000）
int n, m; // n：樱花树数，m：总时间
int t[N], c[N], p[N];
int dp[M];

void zero_one_pack(int v, int w) {
    for (int j = m; j >= v; j--) {
        dp[j] = max(dp[j], dp[j - v] + w);
    }
}

void complete_pack(int v, int w) {
    for (int j = v; j <= m; j++) {
        dp[j] = max(dp[j], dp[j - v] + w);
    }
}

void multiple_pack(int v, int w, int x) {
    int cnt = x;
    int k = 1;
    while (cnt >= k) {
        zero_one_pack(k * v, k * w);
        cnt -= k;
        k *= 2;
    }
    if (cnt > 0) {
        zero_one_pack(cnt * v, cnt * w);
    }
}

int main() {
    // 读取时间：T_s和T_e转换为分钟差
    int h1, m1, h2, m2;
    char ch;
    cin >> h1 >> ch >> m1 >> h2 >> ch >> m2 >> n;
    m = h2 * 60 + m2 - (h1 * 60 + m1);

    for (int i = 1; i <= n; i++) {
        cin >> t[i] >> c[i] >> p[i];
    }

    memset(dp, 0, sizeof dp);

    for (int i = 1; i <= n; i++) {
        if (p[i] == 0) {
            // 完全背包
            complete_pack(t[i], c[i]);
        } else if (p[i] == 1) {
            // 01背包
            zero_one_pack(t[i], c[i]);
        } else {
            // 多重背包
            multiple_pack(t[i], c[i], p[i]);
        }
    }

    cout << dp[m] << endl;
    return 0;
}

示例输入

6:50 7:00 3
2 1 0
3 3 1
4 5 4

示例输出

11

解释

• 总时间：10 分钟；
• 树 1（完全背包）：时间 2，价值 1，可看 5 次（10/2=5），价值 5；
• 树 2（01 背包）：时间 3，价值 3，看 1 次，价值 3；
• 树 3（多重背包）：时间 4，价值 5，最多 4 次，选 1 次（4 分钟），价值 5；
• 最优组合：树 2（3 分钟，3）+ 树 3（4 分钟，5）+ 树 1（3 分钟，1.5→1 次，1）？不对，正确组合：树 3 两次（8 分钟，10）+ 树 1 一次（2 分钟，1）→ 总价值 11。

五、多维费用背包：多重约束下的 "权衡选择"

5.1 问题定义

多维费用背包的核心约束是：背包的约束条件不止一个（如体积 + 重量、时间 + 金钱、人数 + 空间等）。

生活化场景：你要组织一次露营，需要选择物品：

• 约束 1：背包容量≤10L（体积约束）；
• 约束 2：总重量≤15kg（重量约束）；
• 物品：帐篷（5L，8kg，价值 20）、睡袋（3L，5kg，价值 15）、背包（2L，3kg，价值 10）。

如何选择能让总价值最大？

多维费用背包的解法，本质是 "状态维度扩展"------ 将一维dp[j]扩展为多维dp[j1][j2]...，每个维度对应一个约束条件。

5.2 核心思路

以二维费用背包（体积V+ 重量W）为例：

1. 状态表示：dp[j][k]：使用不超过j的体积和k的重量，能获得的最大价值；

2. 状态转移：对于物品（v，w，val），按 01 背包的 "逆序枚举" 更新：

   dp[j][k] = max(dp[j][k], dp[j - v][k - w] + val)

3. 扩展：三维及以上费用背包，同理扩展状态维度和枚举维度。

5.3 代码实现（二维费用版）

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;

const int V = 110; // 体积最大值
const int W = 110; // 重量最大值
int dp[V][W]; // dp[j][k]：体积j，重量k的最大价值

int main() {
    // 示例输入：体积约束10，重量约束15，3个物品
    int max_v = 10, max_w = 15;
    int items[3][3] = {
        {5, 8, 20},  // 帐篷：体积5，重量8，价值20
        {3, 5, 15},  // 睡袋：体积3，重量5，价值15
        {2, 3, 10}   // 背包：体积2，重量3，价值10
    };

    memset(dp, 0, sizeof dp);

    // 二维费用背包：01背包逻辑，逆序枚举体积和重量
    for (int i = 0; i < 3; i++) {
        int v = items[i][0], w = items[i][1], val = items[i][2];
        // 体积逆序
        for (int j = max_v; j >= v; j--) {
            // 重量逆序
            for (int k = max_w; k >= w; k--) {
                dp[j][k] = max(dp[j][k], dp[j - v][k - w] + val);
            }
        }
    }

    cout << "二维费用背包最大价值：" << dp[max_v][max_w] << endl; // 输出45
    return 0;
}

5.4 实战案例：洛谷 P1910 L 国的战斗之间谍

题目链接：https://www.luogu.com.cn/problem/P1910

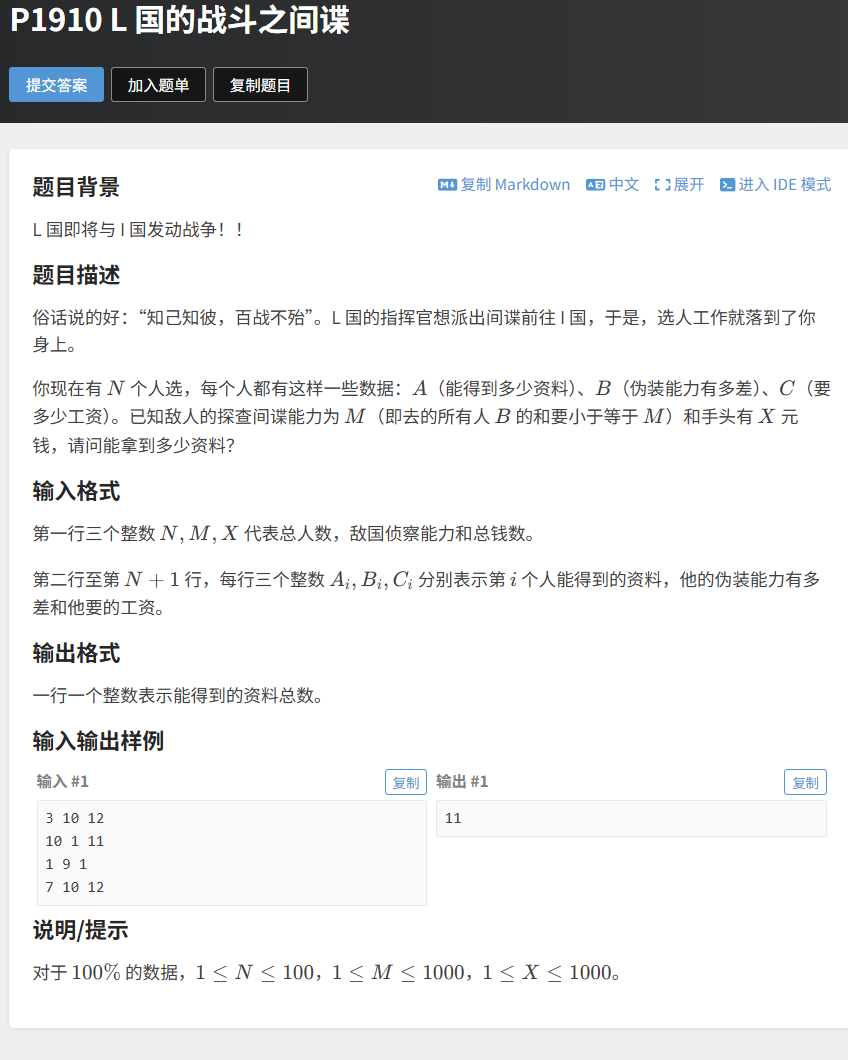
题目描述

有N个人选，每个人有资料价值A[i]、伪装能力B[i]（越小越差）、工资C[i]。敌国探查能力M（总伪装能力≤M），手头有X元（总工资≤X）。求能拿到的最大资料价值。

分析

二维费用背包：

• 约束 1：总伪装能力≤M；
• 约束 2：总工资≤X；
• 物品：每个人（01 背包，只能选一次）；
• 目标：最大资料价值。

代码实现

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;

const int M = 1010; // 伪装能力最大值
const int X = 1010; // 工资最大值
int dp[M][X]; // dp[j][k]：伪装j，工资k的最大资料价值

int main() {
    int N, max_B, max_C;
    cin >> N >> max_B >> max_C;

    int A[N+1], B[N+1], C[N+1];
    for (int i = 1; i <= N; i++) {
        cin >> A[i] >> B[i] >> C[i];
    }

    memset(dp, 0, sizeof dp);

    // 二维费用01背包
    for (int i = 1; i <= N; i++) {
        int a = A[i], b = B[i], c = C[i];
        // 伪装能力逆序
        for (int j = max_B; j >= b; j--) {
            // 工资逆序
            for (int k = max_C; k >= c; k--) {
                dp[j][k] = max(dp[j][k], dp[j - b][k - c] + a);
            }
        }
    }

    cout << dp[max_B][max_C] << endl;
    return 0;
}

示例输入

3 10 12
10 1 11
1 9 1
7 10 12

示例输出

11

解释

• 选择第 1 个人（资料 10，伪装 1，工资 11）+ 第 2 个人（资料 1，伪装 9，工资 1）：
  • 总伪装：1+9=10≤10，总工资：11+1=12≤12；
  • 总资料价值：10+1=11，为最优解。

六、四大扩展模型对比总结

模型	核心约束	状态表示	核心操作	时间复杂度
多重背包	物品最多选x[i]次	一维dp[j]	二进制拆分 / 暴力枚举次数	O(n*T*log(max_x))
分组背包	每组最多选一个物品	一维dp[j]	组内 01 背包（右到左枚举）	O(n*T)
混合背包	同时存在 01 / 完全 / 多重物品	一维dp[j]	分类处理，按对应模型求解	取决于各模型占比
多维费用背包	多重资源约束（如体积 + 重量）	多维dp[j1][j2]	逆序枚举每个约束维度	O(n*T1*T2*...*Tk)

口诀：

• 多重背包：次数有限，二进制拆分变 01；
• 分组背包：组内互斥，组间顺序组内逆；
• 混合背包：规则混杂，分类处理各归各；
• 多维背包：约束多重，状态扩维逆序枚举。

七、常见误区与优化技巧

7.1 常见误区

1. 多重背包忘记二进制拆分，导致超时；
2. 分组背包容量枚举顺序错误（左到右），导致同一组选多个物品；
3. 混合背包对物品类型判断错误，采用了错误的枚举顺序；
4. 多维背包状态维度顺序搞反，或枚举顺序不是逆序，导致重复选择。

7.2 优化技巧

1. 空间优化：多维背包可采用 "滚动数组" 优化空间（如二维转一维，需注意枚举顺序）；
2. 预处理：多重背包的二进制拆分可提前完成，避免重复计算；
3. 剪枝：对于超出容量的物品，直接跳过，减少无效枚举；
4. 数据类型：当价值或容量较大时，使用long long避免溢出。

---

总结

背包问题的扩展模型，本质是基础背包逻辑的 "组合" 与 "扩展"。无论是多重背包的次数约束、分组背包的互斥约束、混合背包的规则混杂，还是多维背包的多重约束，核心都离不开 "状态表示" 和 "状态转移" 这两个动态规划的灵魂。

学习这些模型的关键，不是死记硬背代码，而是理解每种约束对应的 "选择规则"，并将其转化为对应的背包逻辑。比如，"次数有限" 对应多重背包的二进制拆分，"互斥选择" 对应分组背包的组内 01 处理，"多重约束" 对应多维状态的扩展。

当你能灵活切换不同背包模型的解法，甚至能应对多种约束叠加的复杂场景时，就真正掌握了背包问题的核心。接下来，不妨尝试做一些综合类的背包题目，将这些模型融会贯通。

如果本文对你有帮助，别忘了点赞、收藏、转发三连～ 有任何疑问或建议，欢迎在评论区留言讨论！