1 论文简介
《用模糊聚类 Fuzzy C-Means 算法实现图像分割》是由王和春和宫迅凯于 1991 年发表在《光学机械》期刊上的一篇论文。该论文针对图像分割中传统方法(如边缘检测和统计直方图法)难以实现非监督自动分割的问题,提出了基于 Fuzzy C-Means (FCM) 聚类算法的图像分割方法,并通过引入塔型数据结构 (PDS) 来显著减少计算量。 FCM 算法的核心在于通过模糊划分和迭代优化,将图像像素根据隶属度自动归类,无需人工干预先验知识。该方法因其非监督、自适应和高效率的特点,被广泛应用于航空图像、遥感图像等多光谱图像的目标识别与分割领域,为计算机视觉和人工智能中的自动图像分析提供了重要工具,并在相关研究中具有一定影响力。
2 算法原理
假设图像数据包含 nnn 个像素点,每个像素点用 ddd 维特征向量表示,即 x={x1,x2,⋯ ,xn}x = \{x_1, x_2, \cdots, x_n\}x={x1,x2,⋯,xn} ,其中 xk∈Rdx_k \in \mathbb{R}^dxk∈Rd 。设定聚类数目 ccc ( 2≤c≤n2 \leq c \leq n2≤c≤n ),并定义模糊划分矩阵 u=(uik)c×nu = (u_{ik}){c \times n}u=(uik)c×n ,其中 uiku{ik}uik 表示第 kkk 个像素点对第 iii 个类别的隶属度,满足以下条件:
- ∑i=1cuik=1\sum_{i=1}^c u_{ik} = 1∑i=1cuik=1 ,保证每个像素点的隶属度总和为 1;
- ∑k=1nuik>0\sum_{k=1}^n u_{ik} > 0∑k=1nuik>0 ,确保每个类别至少包含一个像素点;
- uik∈[0,1]u_{ik} \in [0,1]uik∈[0,1] ,限定隶属度在 0 到 1 之间。
算法的目标是通过迭代优化,最小化目标函数:
Jm(u,v)=∑k=1n∑i=1cuikm∥xk−vi∥2J_m(u,v) = \sum_{k=1}^n \sum_{i=1}^c u_{ik}^m \| x_k - v_i \|^2Jm(u,v)=k=1∑ni=1∑cuikm∥xk−vi∥2
其中 v=(v1,v2,⋯ ,vc)v = (v_1, v_2, \cdots, v_c)v=(v1,v2,⋯,vc) 是聚类中心向量, vi∈Rdv_i \in \mathbb{R}^dvi∈Rd , m∈[1,∞)m \in [1, \infty)m∈[1,∞) 是隶属度加权因子, ∥⋅∥\| \cdot \|∥⋅∥ 表示欧氏距离范数。具体迭代步骤如下:
- 初始化参数 :设定聚类数 ccc 、初始模糊矩阵 u(0)u^{(0)}u(0) 、收敛阈值 ϵ>0\epsilon > 0ϵ>0 和加权因子 mmm ,迭代计数器 p=0p = 0p=0 。
- 计算聚类中心 :根据当前模糊矩阵 u(p)u^{(p)}u(p) ,更新聚类中心:
vi(p)=∑k=1n(uik(p))mxk∑k=1n(uik(p))mv_i^{(p)} = \frac{\sum_{k=1}^n (u_{ik}^{(p)})^m x_k}{\sum_{k=1}^n (u_{ik}^{(p)})^m}vi(p)=∑k=1n(uik(p))m∑k=1n(uik(p))mxk - 更新隶属度 :根据当前聚类中心,重新计算隶属度:
uik(p+1)=(∑j=1c(∥xk−vi(p)∥∥xk−vj(p)∥)2/(m−1))−1u_{ik}^{(p+1)} = \left( \sum_{j=1}^c \left( \frac{\| x_k - v_i^{(p)} \|}{\| x_k - v_j^{(p)} \|} \right)^{2/(m-1)} \right)^{-1}uik(p+1)= j=1∑c(∥xk−vj(p)∥∥xk−vi(p)∥)2/(m−1) −1 - 检查收敛性 :计算模糊矩阵的变化量 ∥u(p+1)−u(p)∥\| u^{(p+1)} - u^{(p)} \|∥u(p+1)−u(p)∥ ,若小于 ϵ\epsilonϵ 则停止迭代;否则令 p=p+1p = p + 1p=p+1 ,返回步骤 2 继续迭代。
迭代结束后,对优化后的模糊矩阵进行清晰化处理:对于每个像素点 xkx_kxk ,将其归入隶属度最大的类别,即若 ui0k=max1≤i≤cuiku_{i_0 k} = \max_{1 \leq i \leq c} u_{ik}ui0k=max1≤i≤cuik ,则将 xkx_kxk 划分到第 i0i_0i0 类,从而实现图像分割。
3 实验结果
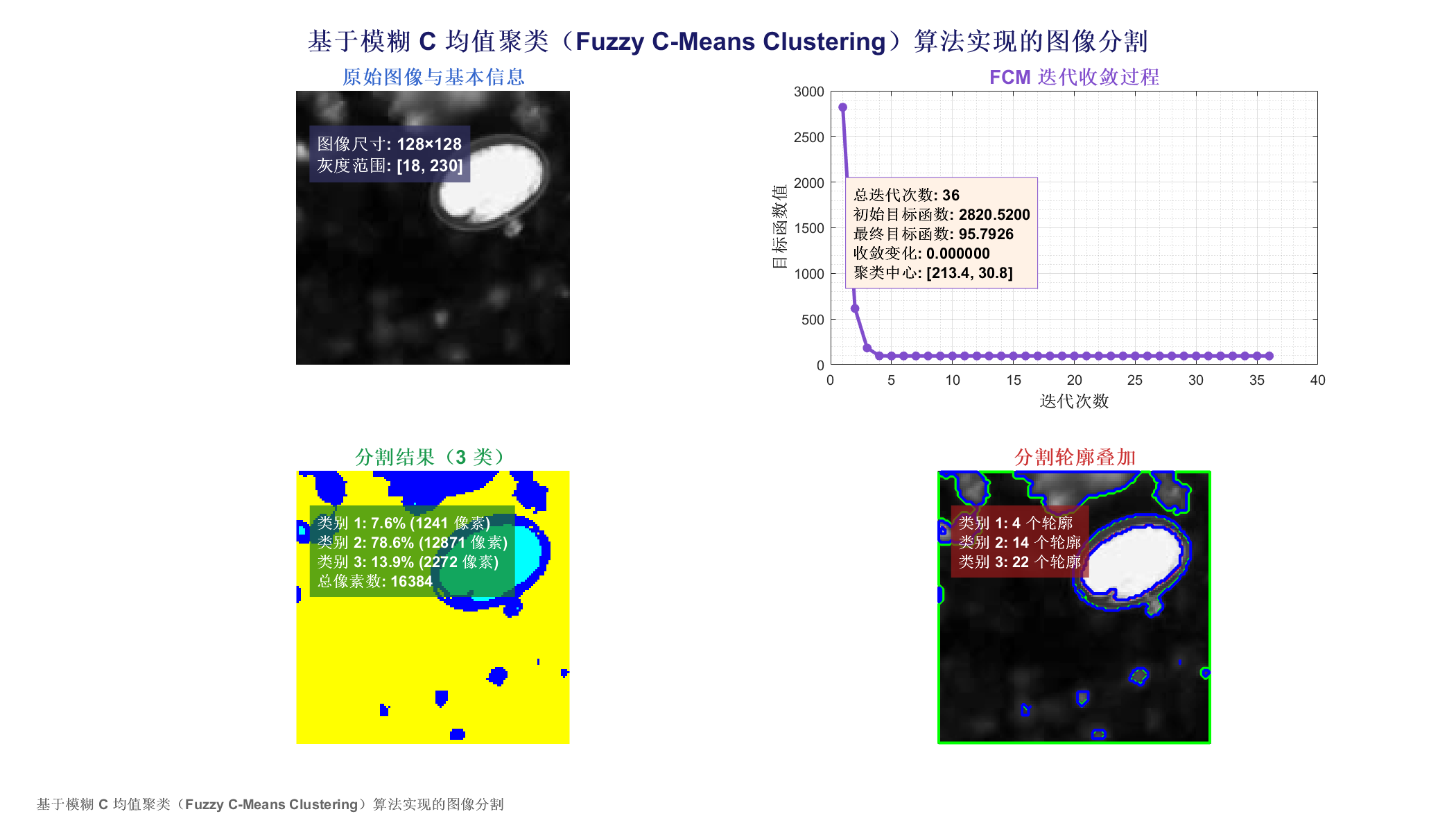
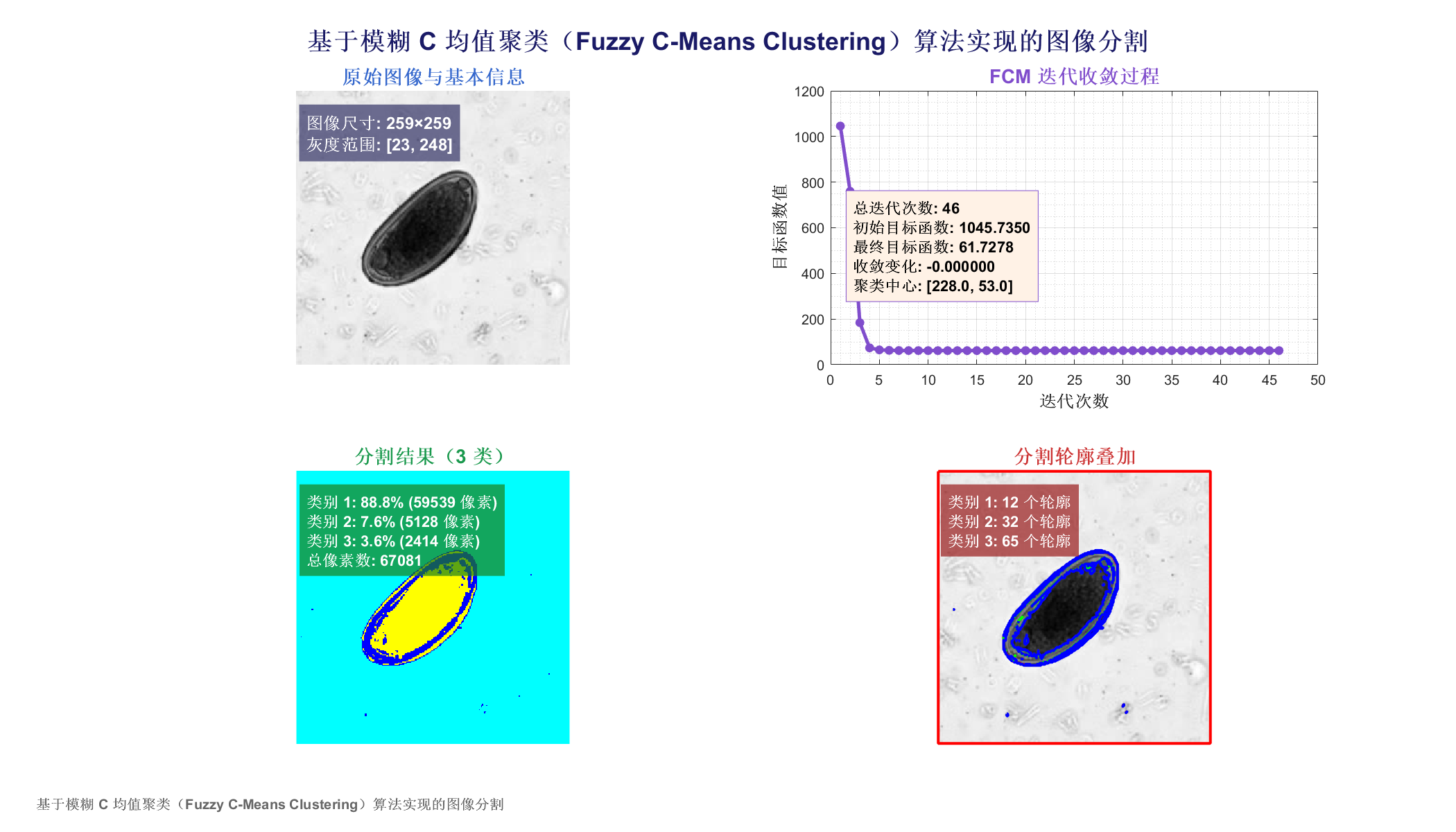
4 参考文献
1\] 王和春, 宫迅凯. 用模糊聚类 Fuzzy C-Means 算法实现图像分割\[J\]. 光学机械, 1991, (04):65-70. \[2\] 丁震, 胡钟山, 杨静宇, 等. FCM 算法用于灰度图象分割的研究\[J\]. 电子学报, 1997, (05):39-43. \[3\] 丁震, 胡钟山, 杨静宇, 等. 一种适用于灰度图像分割的快速 FCM 算法\[J\]. 模式识别与人工智能, 1997, 10(02):133-139. ## 5 MATLAB 代码