论文笔记（一百一）Robot Learning from a Physical World Model

Robot Learning from a Physical World Model

文章概括
ABSTRACT
[I. INTRODUCTION（引言）](#I. INTRODUCTION（引言）)
[II. RELATED WORKS（相关工作）](#II. RELATED WORKS（相关工作）)
[III. METHOD（方法）](#III. METHOD（方法）)
- [A. Physical World Modeling from Video Generation （A. 从视频生成中进行物理世界建模）](#A. Physical World Modeling from Video Generation （A. 从视频生成中进行物理世界建模）)
- - [Video generation（视频生成）](#Video generation（视频生成）)
  - [Geometry-aligned 4D reconstruction（几何对齐的4D重建）](#Geometry-aligned 4D reconstruction（几何对齐的4D重建）)
  - [Textured mesh generation（带纹理网格生成）](#Textured mesh generation（带纹理网格生成）)
  - [Physical scene reconstruction and alignment（物理场景重建与对齐）](#Physical scene reconstruction and alignment（物理场景重建与对齐）)
- [B. Object-Centric Learning from the Physical World Model 基于物理世界模型的以物体为中心的学习）](#B. Object-Centric Learning from the Physical World Model 基于物理世界模型的以物体为中心的学习）)
[IV. EXPERIMENTS](#IV. EXPERIMENTS)
- [A. Video Generation Enables Generalizable Manipulation 视频生成实现可泛化的操作](#A. Video Generation Enables Generalizable Manipulation 视频生成实现可泛化的操作)
- [B. World Modeling Improves Manipulation Robustness 世界建模提升操作鲁棒性](#B. World Modeling Improves Manipulation Robustness 世界建模提升操作鲁棒性)
- [C. Object-Centric Learning Enhances Policy Effectiveness 以物体为中心的学习提升策略有效性](#C. Object-Centric Learning Enhances Policy Effectiveness 以物体为中心的学习提升策略有效性)
[V. CONCLUSION](#V. CONCLUSION)

文章概括

引用：

bash 复制代码

@article{mao2025robot,
  title={Robot Learning from a Physical World Model},
  author={Mao, Jiageng and He, Sicheng and Wu, Hao-Ning and You, Yang and Sun, Shuyang and Wang, Zhicheng and Bao, Yanan and Chen, Huizhong and Guibas, Leonidas and Guizilini, Vitor and others},
  journal={arXiv preprint arXiv:2511.07416},
  year={2025}
}

markup 复制代码

Mao, J., He, S., Wu, H.N., You, Y., Sun, S., Wang, Z., Bao, Y., Chen, H., Guibas, L., Guizilini, V. and Zhou, H., 2025. Robot Learning from a Physical World Model. arXiv preprint arXiv:2511.07416.

主页：
原文：
代码、数据和视频：

系列文章：

请在《《《文章》》》专栏中查找

宇宙声明！

引用解析部分属于自我理解补充，如有错误可以评论讨论然后改正！

ABSTRACT

我们提出 PhysWorld：一个通过物理世界建模，使机器人能够从视频生成中进行学习的框架。近年来的视频生成模型能够根据语言指令和图像合成逼真的视觉示范，为机器人学习提供了一种强大但尚未被充分挖掘的训练信号来源。然而，将生成视频中的像素运动直接重定向到机器人会忽略物理规律，往往导致操控不准确。 PhysWorld 通过将视频生成与物理世界重建相结合来解决这一局限。给定一张单幅图像和一条任务指令，我们的方法会生成任务条件化视频，并从这些视频中重建其背后的物理世界；随后借助物理世界模型，通过以物体为中心的残差强化学习，将生成视频中的运动"落地"为符合物理的精确动作。这种协同机制把隐式的视觉引导转化为可在物理上执行的机器人轨迹，免除了真实机器人数据采集的需求，并实现零样本（zero-shot）的可泛化机器人操控。在多种真实世界任务上的实验表明，与以往方法相比，PhysWorld 显著提升了操控精度。更多细节请访问项目网页。

一、强化学习到底在"学"什么？

在最标准的强化学习（RL）里，智能体学的是一个策略 π θ ( a ∣ s ) \pi_\theta(a \mid s) πθ(a∣s) 意思是：

在状态 s s s 下，直接输出一个动作 a a a。

比如：

s s s：当前相机看到的画面 + 物体位置

a a a：机器人关节角度 / 末端速度

传统 RL 的特点：

👉 动作是"从零开始学"的

👉 模型要自己决定"一切该怎么动"

这在真实机器人 + 物理世界 里非常难学、样本极其昂贵。
二、什么是「残差强化学习」（Residual Reinforcement Learning）？

1️⃣ 核心思想（一句话版）

不要让 RL 从零学动作，而是让它只学"修正量（残差）"。

2️⃣ 数学形式（非常关键）

残差 RL 不直接输出动作 a a a，而是：

a = a base + Δ a RL a = a_{\text{base}} + \Delta a_{\text{RL}} a=abase+ΔaRL

其中：

a base a_{\text{base}} abase：

👉 已有的、可信的动作

规则控制器（PID）

规划器（MPC）

模仿学习 / 视频生成得到的动作

Δ a RL \Delta a_{\text{RL}} ΔaRL：

👉 RL 学到的"小修正"

所以 RL 解决的不是「我该怎么动」，而是：

"这个动作大致对了，但哪里不够好，我补一点？"

3️⃣ 为什么残差 RL 很重要？

直接 RL 残差 RL

动作空间大修正量小

难收敛更稳定

容易出危险动作有安全基线

样本效率低样本效率高

👉 这是机器人 RL 里非常成熟、非常工程化的一条路线

典型代表：

Johannink et al., Residual Reinforcement Learning for Robot Control, ICRA 2019

4️⃣ 用一个直觉类比（非常重要）

就像自动驾驶里的方向盘辅助

基础控制器：稳稳往前开

RL：在弯道、湿滑、误差时微调方向

直接 RL	残差 RL
动作空间大	修正量小
难收敛	更稳定
容易出危险动作	有安全基线
样本效率低	样本效率高

I. INTRODUCTION（引言）

近年来生成模型的进展使得能够直接从图像和语言指令合成逼真的视频。在大规模互联网数据上训练的视频生成模型，在多样化场景中展现出很强的泛化能力。对于机器人领域而言，这类模型为操控提供了强大的视觉引导来源。给定机器人的观测和任务指令，视频生成器可以生成一个展示任务完成过程的示范。这些生成视频天然地包含物体动力学与具身运动信息，可用于学习具有泛化能力的机器人操控策略。

尽管视频生成前景巨大，但将生成的像素运动转换为可执行的机器人动作仍然极具挑战。以往工作 [1]--[5] 通过学习逆动力学或策略模型，使生成视频帧与真实机器人动作对齐。然而，这类方法通常依赖大规模真实世界示范来进行对齐，而大规模采集真实示范代价高且耗费人力。另一类方法 [6]--[8] 提出从生成视频中直接跟随视觉线索（例如光流、稀疏轨迹或物体姿态）来提取机器人动作。然而，将视频运动直接重定向到机器人会忽略底层物理约束，往往导致操控不准确。

我们认为，将生成视频与机器人动作连接起来的关键瓶颈在于物理可行性。视频生成尽管具备泛化能力，但对机器人任务而言它提供的是视觉上的合理性而非物理上的准确性；而在真实世界运行的机器人需要物理准确的动作才能正确与物体交互。我们通过引入一个由生成视频构建的代理物理世界模型来解决这一矛盾。该世界模型提供真实的物理反馈，使机器人能够以可扩展的方式、在物理一致的条件下模仿生成视频中的运动。

为此，我们提出 PhysWorld------一个从视频生成出发、进行物理落地（physically grounded）的机器人学习框架。 PhysWorld 的核心在于物理世界重建与视频生成之间的协同：视频生成提供任务执行的像素级视觉引导，而物理世界模型为从这些视觉引导中学习提供真实的反馈。具体而言，给定一张 RGB-D 图像和一条任务提示，我们的方法首先生成一个任务条件化视频，从视觉上展示任务如何完成。接着，我们提出一种新方法，从该视频中构建一个可进行物理交互的场景。最后，我们引入一种以物体为中心的残差强化学习方法，将视频生成与物理世界重建连接起来，从而产生物理准确的机器人动作。我们的框架只需要一张 RGB-D 图像和一条语言指令，却能输出可执行动作以遵循指令完成任务。通过显式建模物理，PhysWorld 消除了对真实世界数据采集的需求，实现零样本（zero-shot）的可泛化机器人操控，并且相较以往方法显著提升操控精度。

我们在一组多样化的真实世界机器人操控任务上评估 PhysWorld。实验结果表明，将视频生成与物理世界建模相结合，能在所有任务上带来显著的精度提升。 PhysWorld 实现了物理落地且具备泛化能力的机器人操控，并在各项实验中稳定地以大幅优势超过现有方法。我们将发布代码与项目资源以促进后续研究。

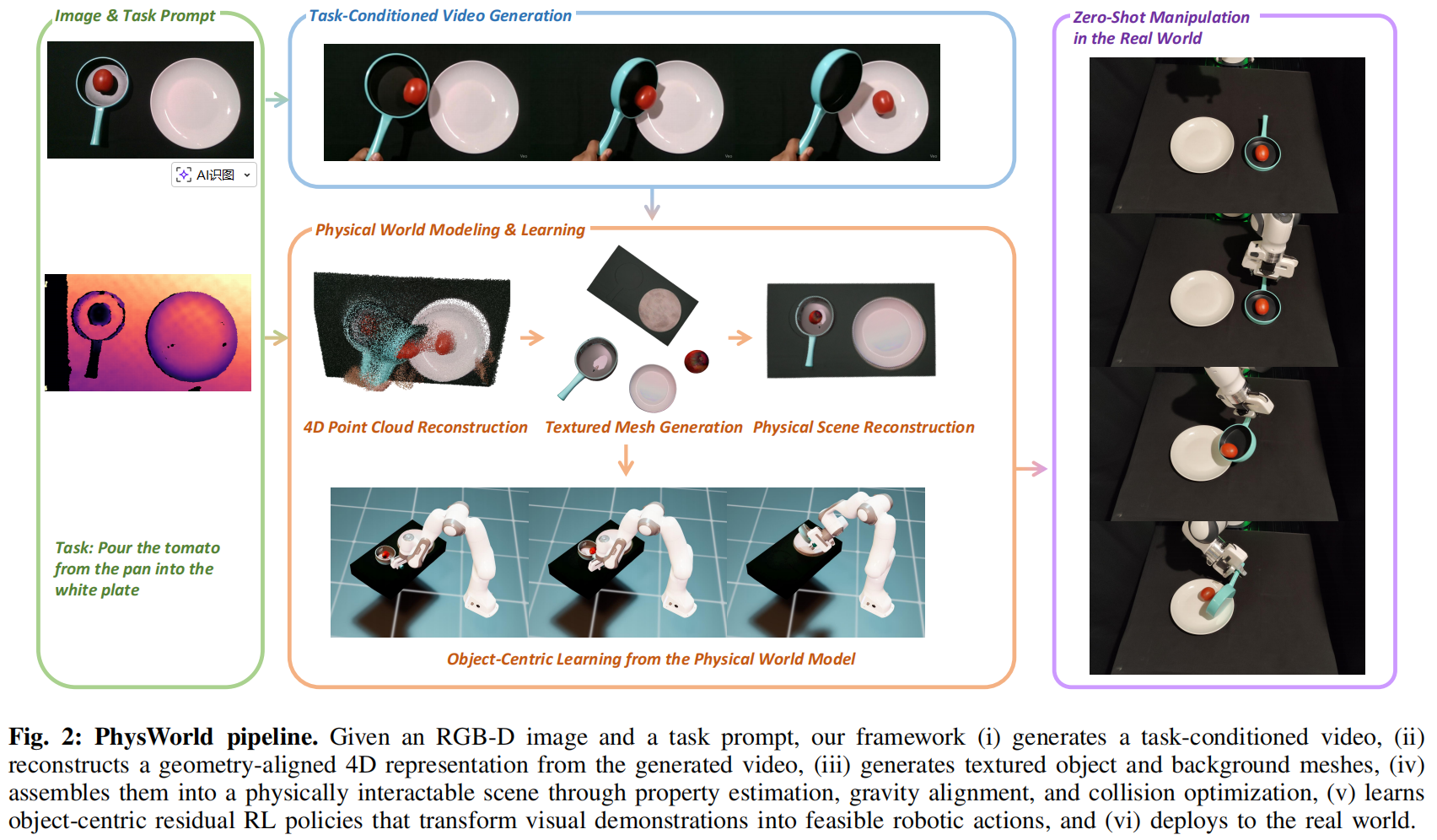
图1：PhysWorld------一个用于从视频生成中进行机器人学习的框架。给定一张图像和一条任务提示作为输入（第1列），我们的方法会生成任务条件化视频（第2列），并重建其背后的物理世界，从而将生成的视觉示范"落地"为在物理上可行的机器人动作（第3列），最终实现真实世界中的零样本（zero-shot）机器人操控（第4列）。

Video generation for robotics（面向机器人的视频生成）

面向机器人的视频生成。视频生成技术 [9]--[11] 对机器人领域具有巨大的潜力。相关研究已将其用于目标生成 [12]、规划 [2], [13]、动力学学习 [14], [15] 以及策略学习 [1], [3]--[8]。为了从生成视频中提取机器人动作，一些工作 [1]--[5], [14], [15] 使用大量真实机器人示范，从生成的视频帧中训练动作模型，但这类数据的采集成本高昂。相比之下，PhysWorld 消除了对真实世界数据采集的需求，并实现了零样本（zero-shot）的机器人操控。另一类方法 [6]--[8] 通过跟随生成视频中的视觉线索（如光流 [6]、稀疏轨迹 [7] 或物体姿态 [8]）来直接提取动作。然而，像素级模仿忽略了物理合理性，往往导致真实世界中的操控不准确。 PhysWorld 则引入了一个代理物理世界模型，使智能体能够在物理反馈的约束下模仿生成视频中的运动，从而提升真实世界机器人操控的准确性与可行性。

Robot learning from videos（从视频中进行机器人学习）

从视频中进行机器人学习。视频包含丰富的运动与任务信息，可用于训练机器人策略。研究者通过学习可迁移表示 [16]--[26]、跟踪与具身无关的运动表示 [27]--[40]、真实到仿真（real-to-sim）[41]--[44]，或强化学习 [45], [46] 等方式来解决这一问题。 PhysWorld 与关于物体姿态跟踪 [8], [36]、真实到仿真重建 [43], [44], [46], [47] 以及强化学习 [43], [46] 的相关工作在理念上具有相似之处。然而，这些方法通常依赖于特定的实验室环境来进行真实到仿真重建和人类示范采集，这限制了它们对"野外"生成视频的泛化能力，而这类视频往往包含运动模糊或视觉幻觉。相比之下，PhysWorld 仅需要一段生成视频即可完成真实到仿真重建，并能够有效地从生成视频中学习物理准确的机器人动作。

Real-to-sim-to-real（真实--仿真--真实）

真实--仿真--真实。真实--仿真--真实方法从观测中重建物理场景，并将其嵌入仿真器中以进行策略学习。为了获得完整的带纹理物体与场景网格 [48] 或高斯点云 [49]，以往工作 [50]--[62] 通常需要专门的多视角采集进行重建，这使其难以应用于单目生成视频。相比之下，PhysWorld 利用生成模型的先验，从单视角视频中建模物理场景，从而无需额外的多视角采集，即可直接从生成视频中进行物理世界建模。

III. METHOD（方法）

我们研究的是开放世界（open-world）机器人操控问题。我们的系统以一张 RGB-D 图像和一条基于语言的任务指令作为输入，输出用于完成任务的、在物理上可行的机器人动作。在方法核心上，我们将视频生成与物理世界建模统一起来：视频生成提供任务执行的像素级视觉引导，而物理世界模型为从这些生成的视觉引导中学习提供真实的反馈。在第 III-A 节中，我们描述如何从生成视频中建模物理世界；在第 III-B 节中，我们详细介绍如何从物理世界模型中学习机器人动作。

A. Physical World Modeling from Video Generation （A. 从视频生成中进行物理世界建模）

视频生成层（像素级指引） ：

给一张图 + 一句指令 → 生成未来 T T T 帧视频

这告诉你"应该怎么动"，但只是视觉上合理。

4D重建层（把视频变成几何+运动） ：

从每帧估深度，拼出"时间一致"的 3D（随时间变化的 4D）。

但它的尺度可能不对（比如物体看起来大一圈/小一圈）。

网格层（让几何能进物理仿真） ：

深度图/点云不能直接当仿真物体 → 要变成 mesh（网格）+纹理。

物理场景层（能仿真） ：

给 mesh 加上质量/摩擦；把场景"重力方向摆正"；避免物体一开始就穿进桌子。

最终得到一个"可交互"的数字孪生体。

在互联网数据上训练的视频生成模型，已经在多种任务和场景中展现出生成视觉示范的卓越能力。然而，这些生成的示范仅提供任务完成的像素级引导，而机器人是在三维空间中运行，并受到物理约束。为弥合这一差距，我们提出首先从生成视频中建模物理世界，将像素级引导转化为具有物理基础的表示，使机器人能够以准确且可行的动作来执行。这种转化并非易事，因为生成视频仅提供物理世界的部分观测，并且常常包含视觉伪影。在本文中，我们提出了一种利用生成先验（generative priors）来有效解决该问题的新方法。具体而言，给定一段生成视频，我们首先估计一个四维时空表示。随后，我们为物体和背景生成带纹理的网格模型，为其赋予物理属性，并将它们与该四维表示对齐，从而构建物理场景。最后，我们从视频中提取四维运动信息，作为策略学习的目标。各个步骤的具体细节将在后续小节中进行介绍。

Video generation（视频生成）

我们的方法支持多种视频生成模型 [9]--[11], [63]，只要它们是带有文本控制的图像到视频（image-to-video）模型即可。给定一张输入图像 I 0 I_0 I0 和一条任务指令，视频生成模型会生成 T T T 个未来帧 { I 1 , ... , I T } \{I_1, \ldots, I_T\} {I1,...,IT}，用于展示任务将如何被完成。在本工作中，我们主要使用 Veo3 [63] 进行视频生成，因为其输出质量较高；同时，我们在消融实验中评估了其他模型。

输入：第一帧图像 I 0 I_0 I0 + 语言任务指令
输出：未来帧 I 1 , ... , I T {I_1,\dots,I_T} I1,...,IT

直觉：

视频生成模型像一个"超级会脑补的导演"：看一眼场景+听你说任务，就给你演一段"任务完成过程"。

但它只保证看起来像 ，不保证物理上对（比如穿模、摩擦不对、物体不可能那样滑动）。

这里的关键点：

他们不限制具体哪个视频模型，只要是image-to-video + text control就行；主要用 Veo3（因为效果好）。

这一步产物是什么地位？ 它是"示范"，但只是像素级示范。后面所有步骤都是在想办法把"像素示范"变成"物理世界里的可执行示范"。

Geometry-aligned 4D reconstruction（几何对齐的4D重建）

生成视频提供的是像素级示范，而对于在真实物理世界中运行的机器人来说，必须将其转换为四维时空表示。为了从视频中获得准确的结构与运动估计，我们使用 MegaSaM[64] 来初始化动态场景重建；该方法会为每一帧生成时间一致的深度估计 { D 0 ′ , ... , D T ′ } \{D_0',\ldots,D_T'\} {D0′,...,DT′}。然而，MegaSaM 的估计结果与真实世界的度量尺度并不对齐。为了解决这一问题，我们利用真实世界采集的深度图像 D 0 D_0 D0 来对输出进行标定（校准）。具体而言，我们求解一个全局的尺度与平移 ( α , β ) (\alpha,\beta) (α,β)，使得在所有有效像素上满足 α D 0 ′ + β ≈ D 0 αD_0'+β≈D_0 αD0′+β≈D0，方法是最小化如下鲁棒回归目标：

min ⁡ α , β ∑ p ∈ Ω w p ( α D 0 ′ ( p ) + β − D 0 ( p ) ) 2 , (1) \min_{\alpha,\beta}\sum_{p\in\Omega}w_p\big(\alpha D_0'(p)+\beta-D_0(p)\big)^2,\tag{1} α,βminp∈Ω∑wp(αD0′(p)+β−D0(p))2,(1)

其中， Ω \Omega Ω 表示有效像素集合， w p w_p wp 是Huber权重，用于降低离群点的影响。随后，将标定得到的参数 ( α , β ) (\alpha,\beta) (α,β) 应用到所有帧的深度 { D t ′ } t = 0 T \{D_t'\}{t=0}^{T} {Dt′}t=0T 上，得到与真实尺度对齐的深度图 { D t } t = 0 T \{D_t\}{t=0}^{T} {Dt}t=0T ，从而实现对场景几何的一致四维时空重建。在已知相机参数的情况下，我们还可以通过反投影（un-projection）得到动态点云 { P t } t = 0 T \{P_t\}_{t=0}^{T} {Pt}t=0T。

Geometry-aligned 4D reconstruction：从视频得到"会动的3D"，还要对齐真实尺度

1 先用 MegaSaM 做什么？

MegaSaM 会对每一帧给一个深度估计： D 0 ′ , ... , D T ′ {D_0',\dots,D_T'} D0′,...,DT′

并且它强调"时间一致"（temporal consistent）------这很重要：

如果每一帧深度都乱跳，你拼出来的3D会抖，运动也会假。

时间一致意味着：同一个物体在连续帧里的深度变化是连贯的，更像真实运动。

2 使用 D 0 D_0 D0 校准

MegaSaM 从"单目视频"推深度时，经常只有相对深度 靠谱，绝对尺度不靠谱。

简单说：

它可能知道"杯子比桌面近"，但不知道"近多少厘米"。

这会导致物理仿真崩掉：尺度不对 → 重力、摩擦、接触都会错。

你这里有真实传感器给的深度 D 0 D_0 D0（RGB-D 的 D），这是有真实单位的（米、毫米）。所以作者做了一件很"工程但关键"的事：

用真实深度 D 0 D_0 D0 去把模型深度 D 0 ′ D_0' D0′ 变成同一尺度。

3 公式(1)到底在干嘛？（鲁棒线性标定）

他们假设只需要一个全局的"缩放+平移"就能对齐：

α D 0 ′ ( p ) + β ≈ D 0 ( p ) \alpha D_0'(p)+\beta \approx D_0(p) αD0′(p)+β≈D0(p)

α \alpha α：把深度整体放大/缩小（尺度校准）

β \beta β：整体加一个偏移（零点/系统误差）

然后在所有有效像素 p ∈ Ω p\in\Omega p∈Ω 上，最小化误差平方：

min ⁡ α , β ∑ p ∈ Ω w p ( α D 0 ′ ( p ) + β − D 0 ( p ) ) 2 \min_{\alpha,\beta}\sum_{p\in\Omega}w_p(\alpha D_0'(p)+\beta-D_0(p))^2 α,βminp∈Ω∑wp(αD0′(p)+β−D0(p))2

这里的 w p w_p wp 是 Huber 权重，作用一句话：

对离群点不那么敏感（比如生成视频有伪影、深度估错特别离谱的像素，不要把拟合带歪）。

结果：得到 ( α , β ) (\alpha,\beta) (α,β)，然后把它用到所有帧： D t = α D t ′ + β , t = 0... T D_t = \alpha D_t' + \beta,\quad t=0...T Dt=αDt′+β,t=0...T

这一步做完，你就有了尺度正确且时间一致的4D几何。

4 "反投影 un-projection"是什么？

已知相机内参时，深度图 D t D_t Dt 可以变成点云 P t P_t Pt：

每个像素 p p p + 深度值 D t ( p ) D_t(p) Dt(p) → 在相机坐标系里的 3D 点

于是得到动态点云序列 P t {P_t} Pt

这就是"把2.5D（深度图）变成3D点云"。
求解最小化误差平方：

min ⁡ α , β ∑ p ∈ Ω w p ( α D 0 ′ ( p ) + β − D 0 ( p ) ) 2 \min_{\alpha,\beta}\sum_{p\in\Omega}w_p(\alpha D_0'(p)+\beta-D_0(p))^2 α,βminp∈Ω∑wp(αD0′(p)+β−D0(p))2

1) 先把式子改成最熟的线性回归形式

定义每个像素点的数据：

x p = D 0 ′ ( p ) x_p = D_0'(p) xp=D0′(p)（模型深度）

y p = D 0 ( p ) y_p = D_0(p) yp=D0(p)（真实深度）

目标函数就是加权最小二乘：

min ⁡ α , β ∑ p ∈ Ω w p ( α x p + β − y p ) 2 \min_{\alpha,\beta}\sum_{p\in\Omega} w_p(\alpha x_p+\beta-y_p)^2 α,βminp∈Ω∑wp(αxp+β−yp)2

如果先忽略 Huber（也就是把 w p w_p wp 当作已知常数），这就是标准的"带权线性回归"。

2) 如果 w p w_p wp 是固定的：闭式解（直接算出来）

令残差 r p = α x p + β − y p r_p=\alpha x_p+\beta-y_p rp=αxp+β−yp。对 α , β \alpha,\beta α,β 求偏导并令其为 0：

对 β \beta β：

∂ ∂ β ∑ w p r p 2 = 2 ∑ w p r p = 0 \frac{\partial}{\partial \beta}\sum w_p r_p^2 =2\sum w_p r_p=0 ∂β∂∑wprp2=2∑wprp=0 即： ∑ w p ( α x p + β − y p ) = 0 \sum w_p(\alpha x_p+\beta-y_p)=0 ∑wp(αxp+β−yp)=0

对 α \alpha α：

∂ ∂ α ∑ w p r p 2 = 2 ∑ w p x p r p = 0 \frac{\partial}{\partial \alpha}\sum w_p r_p^2 =2\sum w_p x_p r_p=0 ∂α∂∑wprp2=2∑wpxprp=0 即： ∑ w p x p ( α x p + β − y p ) = 0 \sum w_p x_p(\alpha x_p+\beta-y_p)=0 ∑wpxp(αxp+β−yp)=0

把它们写成"加权统计量"的形式会非常清晰。定义：

S w = ∑ w p , S x = ∑ w p x p , S y = ∑ w p y p S_w=\sum w_p,\quad S_x=\sum w_p x_p,\quad S_y=\sum w_p y_p Sw=∑wp,Sx=∑wpxp,Sy=∑wpyp S x x = ∑ w p x p 2 , S x y = ∑ w p x p y p S_{xx}=\sum w_p x_p^2,\quad S_{xy}=\sum w_p x_p y_p Sxx=∑wpxp2,Sxy=∑wpxpyp

两条方程变成：

α S x + β S w = S y \alpha S_x+\beta S_w=S_y αSx+βSw=Sy α S x x + β S x = S x y \alpha S_{xx}+\beta S_x=S_{xy} αSxx+βSx=Sxy

解这个 2×2 线性方程组（求 α , β \alpha,\beta α,β）：

分母 Δ = S w S x x − S x 2 \Delta=S_wS_{xx}-S_x^2 Δ=SwSxx−Sx2

解 α = S w S x y − S x S y Δ , β = S x x S y − S x S x y Δ \alpha=\frac{S_wS_{xy}-S_xS_y}{\Delta},\qquad \beta=\frac{S_{xx}S_y-S_xS_{xy}}{\Delta} α=ΔSwSxy−SxSy,β=ΔSxxSy−SxSxy

这就是"怎么算"的最直接答案：把所有有效像素的 x p , y p , w p x_p,y_p,w_p xp,yp,wp 累加成 5 个和（ S w , S x , S y , S x x , S x y S_w,S_x,S_y,S_{xx},S_{xy} Sw,Sx,Sy,Sxx,Sxy），然后套公式。

3) 但式子里写了 Huber 权重： w p w_p wp 怎么来的？

Huber 的意思是：离群点（误差特别大）别让它主宰拟合 。最常见的做法不是一次算完，而是用 IRLS（迭代重加权最小二乘）：

先给初始权重 w p = 1 w_p=1 wp=1（或用一个粗略初值）

用上面闭式解算出 ( α , β ) (\alpha,\beta) (α,β)

计算残差： r p = α x p + β − y p r_p=\alpha x_p+\beta-y_p rp=αxp+β−yp

用 Huber 规则更新权重（典型形式）给一个阈值 δ \delta δ：
w p = { 1 , ∣ r p ∣ ≤ δ δ ∣ r p ∣ , ∣ r p ∣ > δ w_p= \begin{cases} 1,& |r_p|\le \delta\ \\ \frac{\delta}{|r_p|},& |r_p|>\delta \end{cases} wp={1,∣rp∣δ,∣rp∣≤δ ∣rp∣>δ
直觉：误差小的点权重=1，误差大的点权重就按 1 / ∣ r ∣ 1/|r| 1/∣r∣ 变小。

重复 2--4，迭代几次就收敛（一般 3--10 次就够）

你论文里写"Huber 权重"基本就是指这类 IRLS 思路：每次用当前误差给点重新分配权重，再做一次加权最小二乘。

Textured mesh generation（带纹理网格生成）

四维重建可以从生成视频中得到结构与运动，但深度图或点云的表示形式不能直接用于物理仿真。网格（mesh）是仿真器中标准的几何表示。以往的真实到仿真（real-to-sim）方法通常依赖 Polycam 或 BundleSDF[65] 等流水线，从完整的多视角扫描中重建网格。然而，这些流水线并不适用于生成的单目视频，因为其中物体和场景往往只能被部分看见。为解决这一挑战，我们提出一种生成式方法，用于恢复完整的物体网格与背景网格。

Textured mesh generation：为什么一定要 mesh？点云不行吗？

最容易卡住的第二个点：仿真器不喜欢点云。

仿真器（物理引擎）通常需要：

连续的表面（mesh）

可计算的碰撞（collision geometry）

可贴材质（纹理只是为了视觉一致，物理主要靠几何）

点云/深度图是"散点"，碰撞不好算，接触也不稳定。所以他们必须把场景变成：

物体 mesh： M o M^o Mo

背景 mesh： M b M^b Mb

但这里有一个大坑：

生成视频是单目视角，很多地方永远看不到（被遮挡/背面/桌子后面）传统多视角扫描（Polycam / BundleSDF）依赖你绕着拍一圈，这里做不到。

所以他们用"生成式方法"补全不可见部分。

给定第一帧图像及其点云几何 I 0 , P 0 I_0, P_0 I0,P0，我们首先在 I 0 I_0 I0 中将物体与背景分离。将物体像素移除后，使用带掩码的图像修复（inpainting）[66] 填补缺失区域，从而得到补全后的背景图像 I b I^b Ib以及每个物体的单独裁剪图 I o I^o Io。对每个物体，我们将图像到三维生成器（image-to-3D generator）[67] 应用于 I o I^o Io，生成一个规范（canonical）的带纹理网格 M o M^o Mo。

1 先做前景/背景分离 + 背景修复 inpainting

给第一帧 I 0 I_0 I0 和点云 P 0 P_0 P0：

分割：把物体像素和背景像素分开

把物体从图里抹掉

用 inpainting 填补抹掉的洞，得到完整背景图 I b I^b Ib

同时裁剪出每个物体的图 I o I^o Io

直觉：

I b I^b Ib：没有物体遮挡的"干净桌面/地面/墙面"

I o I^o Io：每个物体的"证件照"

2 物体 mesh 怎么来？image-to-3D generator

对每个物体裁剪图 I o I^o Io，送进 image-to-3D 生成器，得到"canonical"网格 M o M^o Mo。

canonical 的意思你可以理解为：

生成器先在一个"默认坐标系/默认摆放方式"里生成一个完整物体模型（含纹理）。

这一步解决了单目看不到背面的问题：生成器靠先验把背面也"脑补"出来。

在背景重建中，我们需要与补全背景图像 I b I^b Ib 相对应的几何 P b P^b Pb。这意味着要推断原本被物体遮挡区域的几何形状。我们通过"物体在地面上（object-on-ground）"的假设来解决：物体由背景支撑，因此其遮挡区域要么是平面的支撑表面，要么向远处延伸到无穷（但受场景边界限制）。具体而言，我们对遮挡像素发射相机射线，并计算这些射线与支撑平面或场景边界的最近交点，从而以一致的几何形状补全 P b P^b Pb。得到 I b , P b I^b, P^b Ib,Pb后，我们通过高度图三角化（height-map triangulation）重建背景网格 M b M^b Mb，并将 I b I^b Ib作为纹理贴图。

3 背景几何 P b P^b Pb 怎么补？

你现在有背景图 I b I^b Ib，但你还缺一个对应的背景几何 P b P^b Pb。关键难点：被物体挡住的那块背景，深度图里根本没有深度。他们用一个非常强的物理/场景先验：object-on-ground 假设

物体是被背景支撑的（在桌面/地面上），所以遮挡区域要么是支撑平面（桌面那一块），要么延伸到场景边界（比如墙/地面远处）。

实现方式（你要抓住"射线"的直觉）：

对被遮挡的像素，发出相机射线

计算射线与"支撑平面"或"场景边界"的交点

用这些交点填出一块"合理的背景几何" P b P^b Pb

这就是：用几何规则补全被遮挡深度。

一、你现在已经有了什么？

一张补全后的背景图片 ： I b I^b Ib
👉 这是颜色/纹理，告诉你"看起来像什么"

一部分真实的背景点云（没被挡住的地方）

但你缺一个关键东西：

👉 被物体挡住的那一块背景的"三维形状"

也就是你说的：

要与 I b I^b Ib 对应的几何 P b P^b Pb

换句话说：

图像你补全了（桌面颜色补出来了）

但桌面那一块在 3D 里到底在哪儿？多高？多远？你不知道

二、为什么这块几何"必须猜"？不能算出来吗？

因为这是单目 + 被遮挡的经典死局：

相机没看到

深度传感器也没看到

视频生成也没提供真实深度

👉 这块区域的信息在物理意义上是"不可观测的" 所以只能靠假设（prior）。

三、他们用的假设到底是什么？（object-on-ground）

论文里一句话，其实是两个非常"人类直觉"的假设：

假设 1：物体是被背景支撑的

也就是：

杯子在桌子上

箱子在地面上

不会悬空，不会贴在墙中间

👉 所以被挡住的那块背景，至少是一块"支撑平面"

假设 2：如果不是支撑平面，那就"向远处延伸"

什么意思？

想象一个场景：

桌子前面放了个箱子

箱子挡住了你看到桌子后半部分

那桌子后面那一块：

要么是同一张桌面继续延伸

要么是地面继续延伸到远处

不可能突然是个洞、悬崖、奇怪形状

👉 这就是"向远处延伸到无穷（受场景边界限制）"

四、现在开始讲最关键的：什么叫"对遮挡像素发射相机射线"？

这一步是整个方法的灵魂 ，我慢慢拆。

1️⃣ 什么是"遮挡像素"？

在原图中：

某些像素原本是桌面/地面

但现在被物体挡住了（杯子、箱子）

这些像素的位置你是知道的（在图像平面上），但：

它们的深度是未知的

2️⃣ 什么是"相机射线"？（非常重要）

这是计算机视觉里的基本操作：

图像里的一个像素 = 从相机出发的一条直线方向

想象你用激光笔：

激光从相机镜头发出

穿过这个像素点

一直往前打

这条"激光路径"，就是相机射线

3️⃣ 他们具体对每个遮挡像素做了什么？

对每一个被物体挡住的像素 p p p：

从相机中心出发

沿着这个像素对应的方向

发射一条射线（想象一根无限长的直线）

然后问一个问题：

这条射线"最先"撞到哪里，才是合理的背景？

五、射线会撞到哪里？只有两种可能（这就是假设落地的地方）

情况 A：撞到"支撑平面"（最常见）

比如：

桌面

地面

他们前面已经用 RANSAC 拟合过平面了（你别忘了那一步）。

RANSAC 在做什么？（一句话）

反复随机挑 3 个点生成一个平面，看看有多少点"贴在这个平面上"，贴得最多的那个平面就是桌面/地面。

所以：

射线 ∩ 桌面平面 = 一个交点

这个交点就是： 👉 "如果没有物体挡着，这个像素看到的桌面点"

这一步本质是在说：

这块被挡住的地方，其实和桌面是同一平面

情况 B：没撞到支撑平面 → 那就延伸到场景边界

比如：

桌面后面是地面

地面一直延伸到远处

于是：

射线继续走

与场景边界（比如最大深度、bbox）相交

取最近的合法交点

这就对应论文里那句：

"向远处延伸到无穷（但受场景边界限制）"

做法：

深度图 -> 点云

在点云中使用RANSAC 拟合过平面找到平面

平面点云投影到2D然后根据RGB图像找到桌子边框

六、这样做完之后， P b P^b Pb 是怎么"补全"的？

现在你可以想象这个过程了：

原来：

有些背景点有真实深度

有些背景点（被遮挡）是"空白"

现在：

对每个空白点

用"射线 + 平面/边界"算出一个 3D 点

👉 最终结果：

所有背景像素（包括原来被挡住的）都有了一个合理的 3D 位置

这整块拼起来，就是 P b P^b Pb
4 背景 mesh 怎么从 I b , P b I^b, P^b Ib,Pb 得到？height-map triangulation

背景通常是一个"相对接近平面+起伏"的东西（桌面/地面），可以看成 height-map（高度图）。三角化就是把高度图变成一张三角网格： M b M^b Mb，再把 I b I^b Ib 贴为纹理。

4.1 什么是"高度图（height-map）"？（这是关键概念）

先给一句傻瓜版定义

高度图 = 把一个表面，看成"每个 (x,y) 位置只有一个高度 z"

也就是说：

对于每个地面位置 ( x , y ) (x,y) (x,y)

只有一个对应的高度 z z z

用最直观的例子理解

想象你在玩 Minecraft：

地图是一个 2D 网格 ( x , y ) (x,y) (x,y)

每个格子有一个"地面高度"

没有洞、没有悬空结构

这就是 height-map

数学上就是一个函数

z = h ( x , y ) z = h(x,y) z=h(x,y)

而不是：

复杂的多层结构

一个 ( x , y ) (x,y) (x,y) 上有多个 z z z

为什么"背景"天然适合用高度图？

背景通常是：

桌面

地面

地板 + 墙角

平缓起伏的平面

它们满足一个非常重要的条件：

从上往下看，每个 ( x , y ) (x,y) (x,y) 位置，只会遇到一个表面

✅ 没有洞 ✅ 没有翻转 ✅ 没有自遮挡

👉 所以可以安全地表示为 height-map

4.2 那 P b P^b Pb 怎么变成"高度图"？

你现在有的是 P b P^b Pb：一堆 3D 点 ( x i , y i , z i ) (x_i, y_i, z_i) (xi,yi,zi)

作者做的事，本质上是：

在一个规则的 ( x , y ) (x,y) (x,y) 网格上，记录每个格子对应的高度 z z z

具体步骤（不涉及复杂数学）：

在地面平面上铺一个 2D 网格（像棋盘一样）

对每个网格格子：

找落在这个格子里的点云

取它们的平均高度 / 最近高度

得到一个规则的"高度矩阵"

你可以想象成一张图：
复制代码
z-values: 
[ 0.00  0.00  0.01  0.02 ] 
[ 0.00  0.01  0.02  0.03 ] 
[ 0.00  0.00  0.01  0.01 ] 
这就是 高度图

4.3 什么是"三角化（triangulation）"？（非常直观）

现在你已经有一个高度图了：

本质是一个规则的 2D 网格

每个网格点有一个高度 z z z

问题来了：

物理引擎 / 渲染器不认"高度矩阵" ，它们只认 三角形网格（triangle mesh）

三角化是什么意思？

把每一个小方格，切成两个三角形

比如一个格子有 4 个点：
复制代码
A ---- B
|      |
|      | 
C ---- D 
你可以切成：

三角形 A-B-C

三角形 B-D-C

这样：

整个表面 = 很多小三角形拼起来

这就是一个 mesh

所以 height-map triangulation 做的事情是：

用 P b P^b Pb 得到规则高度图

在 ( x , y ) (x,y) (x,y) 平面上生成规则网格

每个格子切成两个三角形

所有三角形拼起来 → 背景网格 M b M^b Mb

4.4 那 I b I^b Ib 是怎么"贴"上去的？

现在你已经有了一个背景 mesh M b M^b Mb，它只有几何，没有颜色。 I b I^b Ib 的作用就是：纹理贴图（texture mapping）

做法非常标准：

I b I^b Ib 是从相机视角得到的背景图

每个 ( x , y ) (x,y) (x,y) 网格点，对应原图中的一个像素

把 I b I^b Ib 当作 UV 纹理贴到 M b M^b Mb 上

结果是：

👉 几何来自 P b P^b Pb 👉 颜色来自 I b I^b Ib

看起来像真实场景，但现在"摸得到、撞得上"

4.5 为什么作者不用这个方法做"物体"？

这是一个非常关键的理解点。因为物体通常不是 height-map

物体有这些特点：

有侧面

有悬空

有自遮挡

从上往下看，一个 ( x , y ) (x,y) (x,y) 位置可能有多个 z z z

例如一个杯子：
复制代码
| |   
| |   
|_|   ← 底
👉 同一个 ( x , y ) (x,y) (x,y)，有杯口、杯壁、杯底

👉 高度图直接失效

所以：

背景 → height-map triangulation（简单、稳）

物体 → image-to-3D 生成完整 mesh（复杂、先验强）

最后，通过配准（registration）对齐并缩放物体网格与背景网格 { M o , M b } \{M^o,M^b\} {Mo,Mb}，使其与观测点云 P 0 P_0 P0 匹配，从而将它们组装成完整场景。

5 Registration：把 canonical 物体模型放回真实位置

目前你的物体 M o M^o Mo 是 canonical 的（默认位置/尺度），背景 M b M^b Mb 在相机坐标下。所以要做配准（registration）：

通过对齐 + 缩放，使 M o , M b {M^o,M^b} Mo,Mb 与观测点云 P 0 P_0 P0 匹配。

直觉：

让生成的"完整物体模型"落在第一帧观测到的点云位置上

同时让它尺寸对、朝向对

做到这一步，你就有"完整场景的几何外壳"。

Physical scene reconstruction and alignment（物理场景重建与对齐）

Physical scene reconstruction & alignment：让它真的能"物理交互"

现在有 mesh 了，但还不能仿真，因为还缺三类"物理必要条件"：

物理属性（质量、摩擦）

重力方向一致（世界坐标）

初始不穿透（否则仿真一开始就爆炸）

从生成视频中，我们得到分解后的场景网格 { M o , M b } \{M^o,M^b\} {Mo,Mb}。为了使这些网格具备可进行物理交互的能力，还需要三个额外步骤：物理属性估计、重力对齐以及碰撞优化。

Physical property estimation（物理属性估计） 物理属性估计会为场景组件分配合适的物理参数，例如质量和摩擦系数。受[68]启发，我们利用视觉-语言模型（VLM）的常识知识来估计这些属性。具体而言，我们将物体类别作为查询输入VLM以获得典型物理参数，并将预测值分配给每个物体及背景，用于后续物理仿真。

他们说"受[68]启发"，用 VLM 的常识：

输入物体类别（比如 "wooden block / ceramic mug / rubber ball"）

VLM 给出典型质量、摩擦系数范围

把这些参数赋给物体和背景

这一步你要理解它的定位：

不是精确测量，是"让仿真别离谱"的合理先验。对于后续策略学习，合理的摩擦/质量比没有强得多。

Gravity alignment（重力对齐） 重力对齐的目的是将 { M o , M b } \{M^o,M^b\} {Mo,Mb} 从相机坐标系变换到世界坐标系，使场景与世界的重力轴一致，这对物理合理的仿真至关重要。我们使用 RANSAC 从分割得到的平面点中估计地面平面法向量 n \mathbf{n} n，并计算使 n \mathbf{n} n 与世界向上轴 e z \mathbf{e}_z ez 对齐的最小旋转：

R grav = exp ⁡ ( [ u ] × θ ) , θ = arccos ⁡ ( n ⊤ e z ) , u = n × e z ∥ n × e z ∥ , (2) \mathbf{R}{\text{grav}}=\exp([\mathbf{u}]\times\theta),\quad \theta=\arccos(\mathbf{n}^\top \mathbf{e}_z),\quad \mathbf{u}=\frac{\mathbf{n}\times \mathbf{e}_z}{\|\mathbf{n}\times \mathbf{e}_z\|},\tag{2} Rgrav=exp([u]×θ),θ=arccos(n⊤ez),u=∥n×ez∥n×ez,(2)

其中， [ u ] × [\mathbf{u}]\times [u]×是向量 u \mathbf{u} u 的反对称（斜对称）矩阵。将 R grav \mathbf{R}{\text{grav}} Rgrav 应用于所有网格后，场景在世界坐标系下与重力方向对齐，从而便于后续物理仿真。

你现在的 mesh 在相机坐标系里。相机坐标系不一定"z轴朝上"。仿真里必须明确：

哪个方向是"上"

重力沿哪个轴

他们做法：

从分割出的平面点里（通常是地面/桌面）用 RANSAC 拟合平面法向量 n \mathbf{n} n

计算一个最小旋转，把 n \mathbf{n} n 对齐到世界向上轴 e z \mathbf{e}_z ez

公式(2)是标准的"轴角旋转"：

旋转角： θ = arccos ⁡ ( n ⊤ e z ) \theta=\arccos(\mathbf{n}^\top \mathbf{e}_z) θ=arccos(n⊤ez) 意思： n \mathbf{n} n 和竖直方向夹角多大

旋转轴： u = n × e z ∣ ∣ n × e z ∣ ∣ \mathbf{u}=\frac{\mathbf{n}\times \mathbf{e}_z}{||\mathbf{n}\times \mathbf{e}_z||} u=∣∣n×ez∣∣n×ez 意思：绕着哪个方向转才能把 n \mathbf{n} n 扳正

最终旋转矩阵： R grav = exp ⁡ ( [ u ] × θ ) \mathbf{R}{\text{grav}}=\exp([\mathbf{u}]\times\theta) Rgrav=exp([u]×θ) 这里 [ u ] × [\mathbf{u}]_\times [u]× 是把向量变成"叉乘矩阵"的常见表示。

你只要记住：

这一步是在"把场景摆正"，让桌面真的水平、重力真的竖直。

1. 这一步实际要做的事情（一句话）

你先从点云里找出"地面/桌面平面"，得到它的法向量 n \mathbf n n，然后算一个旋转矩阵 R R R，把 n \mathbf n n 旋到 e z \mathbf e_z ez。

也就是让： R grav n = e z \mathbf R_{\text{grav}}\mathbf n = \mathbf e_z Rgravn=ez

（严格说是方向对齐，长度无所谓。）

2. 先搞清楚每个符号到底代表什么

2.1 n \mathbf n n 是什么？

n \mathbf n n 是地面平面的法向量。想象桌面是一张纸，它"朝上"的方向就是法向量。

如果桌面完全水平： n \mathbf n n 应该接近 [ 0 , 0 , 1 ] ⊤ [0,0,1]^\top [0,0,1]⊤（或相反方向 [ 0 , 0 , − 1 ] ⊤ [0,0,-1]^\top [0,0,−1]⊤）

如果桌面倾斜： n \mathbf n n 就会歪。

他们用 RANSAC 去拟合平面，是因为点云里有噪声、有物体点、有离群点。RANSAC能在"乱七八糟的点"里稳稳找到"最大的一片平面"。

2.2 e z \mathbf e_z ez 是什么？

世界坐标系的"向上"单位向量： e z = [ 0 , 0 , 1 ] ⊤ \mathbf e_z=[0,0,1]^\top ez=[0,0,1]⊤

你可以把它理解成：仿真里"上"就是它，重力就是沿 − e z -\mathbf e_z −ez。

3. 旋转怎么求？这条公式到底在做什么？

你要的旋转是"最小旋转"（最短路），也就是只转必要的角度，不瞎转。

3.1 旋转角度 θ \theta θ：两根向量夹角

θ = arccos ⁡ ( n ⊤ e z ) \theta=\arccos(\mathbf n^\top \mathbf e_z) θ=arccos(n⊤ez)

n ⊤ e z \mathbf n^\top \mathbf e_z n⊤ez 是两向量的点积（都单位化时等于 cos ⁡ θ \cos\theta cosθ）

所以 arccos ⁡ \arccos arccos 就得到夹角

直觉：

桌面法向量离"竖直向上"差多少度，就转多少度。

3.2 旋转轴 u \mathbf u u：绕哪根轴转才能把它扳正？

u = n × e z ∣ ∣ n × e z ∣ ∣ \mathbf u=\frac{\mathbf n\times \mathbf e_z}{||\mathbf n\times \mathbf e_z||} u=∣∣n×ez∣∣n×ez

叉积 n × e z \mathbf n\times \mathbf e_z n×ez 得到一根同时垂直于 n \mathbf n n 和 e z \mathbf e_z ez 的方向。

直觉：

把一根"歪着的箭头 n \mathbf n n"掰到"竖直箭头 e z \mathbf e_z ez"，你要沿着"垂直于这两个箭头所在平面"的那根轴去转。那根轴就是叉积方向。

再除以范数，是把它变成单位轴。

4. 最关键的： exp ⁡ ( [ u ] × θ ) \exp([\mathbf u]_\times\theta) exp([u]×θ)

你可以把它理解成"把轴角（axis-angle）变成旋转矩阵"的标准公式：Rodrigues / 李群 SO(3) 的指数映射 。

4.1 [ u ] × [\mathbf u]_\times [u]× 是什么？

它是把向量 u = [ u x , u y , u z ] ⊤ \mathbf u=[u_x,u_y,u_z]^\top u=[ux,uy,uz]⊤ 变成一个矩阵：
$u \] × = \[ 0 − u z u y u z 0 − u x − u y u x 0 \] \[\\mathbf u\]_\\times= \\begin{bmatrix} 0 \& -u_z \& u_y \\\\ u_z \& 0 \& -u_x \\\\ -u_y \& u_x \& 0 \\end{bmatrix} \[u\]×= 0uz−uy−uz0uxuy−ux0 它的作用：对任何向量 v \\mathbf v v，都有 \[ u \] × v = u × v \[\\mathbf u\]_\\times \\mathbf v = \\mathbf u \\times \\mathbf v \[u\]×v=u×v 也就是说：这个矩阵就是"叉乘算子"。 4.2 为什么要指数 exp ⁡ \\exp exp？在 3D 里，"绕轴旋转 θ \\theta θ"对应的旋转矩阵可以写成： R = exp ⁡ ( \[ u \] × θ ) \\mathbf R = \\exp(\[\\mathbf u\]_\\times \\theta) R=exp(\[u\]×θ) 你不需要真的去算矩阵指数（工程上通常用 Rodrigues 公式）： **Rodrigues 公式：** R = I + sin ⁡ θ \[ u \] × + ( 1 − cos ⁡ θ ) \[ u \] × 2 \\mathbf R = \\mathbf I + \\sin\\theta\[\\mathbf u\]_\\times + (1-\\cos\\theta)\[\\mathbf u\]_\\times\^2 R=I+sinθ\[u\]×+(1−cosθ)\[u\]×2 这就很直观了：就是用 sin ⁡ \\sin sin、 cos ⁡ \\cos cos 把旋转拼出来。 **5. 应用到网格：到底怎么变换点？** 网格 M M M 里每个顶点是一个 3D 点 x \\mathbf x x（相机坐标系）。做重力对齐就是： x world = R grav , x cam \\mathbf x_{\\text{world}} = \\mathbf R_{\\text{grav}},\\mathbf x_{\\text{cam}} xworld=Rgrav,xcam （这一步只有旋转，没有平移；平移通常另做，比如把地面挪到 z = 0 z=0 z=0。）对所有物体网格 M o M\^o Mo 和背景网格 M b M\^b Mb 的顶点都做一遍，整个场景就被"扳正"。$

Collision optimization（碰撞优化） 碰撞优化旨在相对于背景网格优化每个物体的放置位置，使所有物体保持最小间隙，从而避免初始碰撞。我们将背景网格体素化为符号距离场（SDF） ϕ bg \phi_{\text{bg}} ϕbg。对每个物体网格 M o M^o Mo，令 V o = { v o , 1 , ... , v o , N o } V_o=\{v_{o,1},\ldots,v_{o,N_o}\} Vo={vo,1,...,vo,No} 表示其网格顶点集合。我们引入一个沿着与重力相反方向的竖直平移 τ o \tau_o τo，并求解：

min ⁡ { τ o } ∑ o 1 N o ∑ i = 1 N o [ max ⁡ ( 0 , − ϕ bg ( v o , i + τ o e z ) ) ] 2 . (3) \min_{\{\tau_o\}}\sum_o\frac{1}{N_o}\sum_{i=1}^{N_o} \Big[\max\big(0,-\phi_{\text{bg}}(v_{o,i}+\tau_o \mathbf{e}_z)\big)\Big]^2.\tag{3} {τo}mino∑No1i=1∑No[max(0,−ϕbg(vo,i+τoez))]2.(3)

其中， e z \mathbf{e}_z ez是单位 z z z 轴方向。该目标函数惩罚穿透（即SDF为负的情况），并通过使用带梯度裁剪与早停的 Adam 进行梯度下降来最小化。该过程保证所有物体相对背景进行调整，从而避免初始碰撞，并为仿真保留一致的间隙。

最终，我们从生成视频中得到一个可进行物理交互的数字孪生体。该物理模型对后续学习过程至关重要，因为它提供了将视觉示范转化为可执行机器人动作所必需的、基于物理的反馈。

这一步是非常物理引擎工程的关键点：如果物体初始就和桌面网格互相穿透，仿真会产生巨大反作用力，数值会炸。他们做法很聪明：只允许每个物体做一个很简单的调整------沿竖直方向平移 τ o \tau_o τo （相当于把物体轻轻抬起来/放下去一点点）。具体怎么算"穿透多少"？用背景的 SDF ϕ bg \phi_{\text{bg}} ϕbg：

SDF：在背景外部为正，内部为负，表面为 0

所以 ϕ bg ( x ) < 0 \phi_{\text{bg}}(x)<0 ϕbg(x)<0 就说明点 x x x 在背景内部（穿进去了）

对物体网格顶点 v o , i v_{o,i} vo,i，平移后是 v o , i + τ o e z v_{o,i}+\tau_o\mathbf{e}_z vo,i+τoez。目标函数(3)：

min ⁡ τ o ∑ o 1 N o ∑ i = 1 N o [ max ⁡ ( 0 , − ϕ bg ( v o , i + τ o e z ) ) ] 2 \min_{{\tau_o}}\sum_o\frac{1}{N_o}\sum_{i=1}^{N_o} \Big[\max(0,-\phi_{\text{bg}}(v_{o,i}+\tau_o \mathbf{e}_z))\Big]^2 τomino∑No1i=1∑No[max(0,−ϕbg(vo,i+τoez))]2

你把它读成中文就是：

如果某个顶点的 SDF 是负的（穿透），就产生惩罚；

穿透越深（负得越大），惩罚越大；

不穿透（SDF ≥ 0）就不罚；

调整 τ o \tau_o τo 让所有顶点尽量不穿透。

他们用 Adam 做梯度下降，并加梯度裁剪、早停，保证稳定。

最终效果：

每个物体相对背景保持一个很小的、稳定的间隙，从而仿真能顺利启动。

B. Object-Centric Learning from the Physical World Model 基于物理世界模型的以物体为中心的学习）

给一段生成视频（它告诉你物体应该怎么动），让机器人在这个物理世界里学会把物体真的推到那个运动轨迹上。

关键：他们不是去学"手怎么动看起来像"，而是学"物体怎么动要对"。

在建立了物理世界模型之后，核心步骤是学习一个能够跟随生成视频示范的机器人策略。视频生成会产生两类运动：具身运动（embodiment motion）和物体运动（object motion）。以往方法 [46] 主要重定向具身运动，但由于运动迁移不准确，往往会带来较大的误差。对于生成视频而言，这一问题会进一步加剧，因为生成视频中常常包含虚构（hallucinated）的机器人或人类手部。相比之下，物体运动较少受到此类伪影的影响，并能为任务执行提供更清晰的视觉引导。基于这一观察，我们聚焦于以物体为中心的学习，并提出一种残差强化学习方法，在物理约束下跟踪物体运动。

为什么要"以物体为中心"？（别跳过这句，它是整段的灵魂）

生成视频里会出现两个运动：

具身运动：视频里可能出现一只手/机器人手臂在动

物体运动：被操作的物体在动

以往方法[46]很多是去"重定向具身运动"：把视频里那只手的像素运动搬到你的机器人手上。

但在生成视频里，这条路很容易炸：

生成模型会"瞎画"一只手：手指数量、关节结构、接触点都可能是假的（hallucination）

你让机器人模仿那只"假手"，必然误差巨大

而物体运动相对更可靠：

即使手是假的，视频里"杯子转了/方块移动了"通常仍然有较强一致性

任务成功也通常只看物体最终状态（放到哪里、旋转多少）

所以他们的核心策略是：

不管视频里手怎么动，我只盯着"物体应该怎么动"。

这就是"object-centric"。

Learning targets（学习目标） 将生成的视觉示范转化为四维时空的学习目标，是训练机器人策略的必要步骤。常用的学习目标包括光流 [6]、物体轨迹 [7] 以及物体位姿 [8]。在本文中，我们采用物体位姿作为跟踪目标，因为相比其他运动表示，物体位姿估计通常更加鲁棒。我们的框架也支持其他形式的运动监督，但这部分留待未来进一步探索。给定估计得到的四维场景表示 { D t } t = 0 T \{D_t\}{t=0}^{T} {Dt}t=0T和 { P t } t = 0 T \{P_t\}{t=0}^{T} {Pt}t=0T，以及物体网格 M o M^o Mo，我们使用 FoundationPose[69] 来恢复逐帧的物体位姿：

{ x t o = [ p t o , q t o ] } t = 0 T , (4) \{\mathbf{x}_t^o=[\mathbf{p}_t^o,\mathbf{q}t^o]\}{t=0}^{T},\tag{4} {xto=[pto,qto]}t=0T,(4)

其中， p t o ∈ R 3 \mathbf{p}_t^o\in\mathbb{R}^3 pto∈R3表示物体的位置， q t o ∈ R 4 \mathbf{q}_t^o\in\mathbb{R}^4 qto∈R4表示其姿态的四元数。这些物体位姿轨迹 { x t o } \{\mathbf{x}_t^o\} {xto}被作为策略学习的监督信号，从而使机器人能够跟踪生成视频中的物体运动。

2. Learning targets：把"视频里的引导"变成"可训练的监督信号"

你要训练策略，必须有一个明确目标（target）。他们列了几种可能的目标：

光流（像素层的速度场）

物体轨迹（可能是2D/3D路径）

物体位姿（position + orientation）

他们选择物体位姿，原因很关键：

光流容易受伪影影响；轨迹可能只给位置不稳；位姿（尤其在有深度+mesh时）通常更鲁棒、可物理解释。

2.1 他们怎么得到"每一帧物体位姿"？

你已经有：

每帧深度 D t {D_t} Dt

每帧点云 P t {P_t} Pt

物体的网格 M o M^o Mo

然后用 FoundationPose 来做逐帧姿态估计，得到：

{ x t o = [ p t o , q t o ] } t = 0 T , (4) \{\mathbf{x}_t^o=[\mathbf{p}_t^o,\mathbf{q}t^o]\}{t=0}^{T},\tag{4} {xto=[pto,qto]}t=0T,(4)

解释清楚这两个量：

p t o ∈ R 3 \mathbf{p}_t^o\in\mathbb{R}^3 pto∈R3：第 t t t 帧目标物体的位置（三维坐标）

q t o ∈ R 4 \mathbf{q}_t^o\in\mathbb{R}^4 qto∈R4：第 t t t 帧目标物体的朝向（四元数）

你可以把 x t o {\mathbf{x}_t^o} xto 理解成：

"生成视频告诉我们：在 t=0...T 的每个时刻，物体应该处在什么位置、朝向什么角度。"

这是后续 RL 的"要追的目标"。

Residual reinforcement learning（残差强化学习） 一种直接的物体位姿跟踪方法[8]是将用于抓取物体的抓取模型[70]与用于后续放置的运动规划器[71]结合起来。然而，在复杂操作任务中，这种策略往往效果不佳：抓取本身就容易失败，而当初始位姿不合适时，运动规划也可能失败。因此，完成一个任务往往需要多次重复抓取和规划，导致效率低下且可靠性下降。强化学习是一种有前景的替代方案，它能够从物理反馈中学习鲁棒策略，但通常需要精心设计的奖励函数以及较长的训练时间才能收敛。为了解决上述问题，我们提出了一种残差强化学习方法，将两种范式的优点结合起来：抓取与运动规划提供基线动作以缩小搜索空间，而强化学习策略在此基础上学习残差修正，从而在物理世界模型的反馈下实现鲁棒适应。形式化地，在给定观测 o t \mathbf{o}_t ot 时，实际执行的动作定义为：

a t = a t base + π θ ( o t ) , (5) \mathbf{a}_t=\mathbf{a}t^{\text{base}}+\pi\theta(\mathbf{o}_t),\tag{5} at=atbase+πθ(ot),(5)

其中， a t base \mathbf{a}t^{\text{base}} atbase是由抓取与运动规划产生的基线动作（同[8]）， π θ ( o t ) \pi\theta(\mathbf{o}_t) πθ(ot)是学习修正调整的残差策略。这种残差形式通过利用物理世界模型的反馈，加速了策略学习并提升了鲁棒性。重要的是，基线动作本身并不需要完全成功，因为学习到的残差可以修正不完美的基线动作，从而完成任务。

3. Residual reinforcement learning：这一段到底在解决什么真实难题？

3.1 传统"抓取+规划"的方法为什么不够？

一种传统流水线是：

先抓起来（抓取模型）

再规划运动把它放到目标位姿（规划器/IK）

问题在复杂操作里很常见：

抓取经常失败（接触、摩擦、姿态不理想）

初始抓得不对 → 后面规划会失败（IK找不到、碰撞、路径不可行）

失败就要"重复抓、重复规划" → 速度慢、可靠性差

3.2 纯强化学习为什么也不够？

纯 RL 能学鲁棒策略，但常见痛点：

奖励要精心设计

训练时间很长

搜索空间大（动作从零学很难）

3.3 他们的解决方案：把两者拼起来（Residual RL）

思路一句话：

规划/抓取先给一个"差不多对"的基线动作，让 RL 只负责"修正"它。

公式就是：

a t = a t base + π θ ( o t ) , (5) \mathbf{a}_t=\mathbf{a}t^{\text{base}}+\pi\theta(\mathbf{o}_t),\tag{5} at=atbase+πθ(ot),(5)

解释每一项：

a t base \mathbf{a}_t^{\text{base}} atbase：基线动作（来自抓取 + 运动规划）

它不一定完美，但通常把你带到"差不多"的区域

π θ ( o t ) \pi_\theta(\mathbf{o}_t) πθ(ot)：RL 学出来的残差（修正量）

负责补偿：摩擦误差、接触误差、模型不准、抓歪了等

为什么这样会更快更稳？

RL 不需要在全动作空间瞎试，只在"基线附近"微调

训练更容易收敛

基线不完美也没关系：残差可以补

你要把它理解成"驾驶辅助"：

规划器像自动驾驶让车大体走在车道中间

RL 像人手微调方向盘，遇到打滑、风、路面变化时修正

Observation and action space（观测与动作空间） 为了提高学习效率，我们采用基于状态的策略。在每个时间步 t t t，策略 π θ ( o t ) \pi_\theta(\mathbf{o}_t) πθ(ot)的观测为：

o t = [ x t ee , x t obj , τ t , x t o , x grasp , d pre , x t base ] , (6) \mathbf{o}_t= [\mathbf{x}_t^\text{ee},\mathbf{x}_t^\text{obj},\tau_t,\mathbf{x}t^o,\mathbf{x}^\text{grasp},d\text{pre},\mathbf{x}_t^\text{base}],\tag{6} ot=[xtee,xtobj,τt,xto,xgrasp,dpre,xtbase],(6)

其中， x t ee \mathbf{x}_t^\text{ee} xtee和 x t obj \mathbf{x}_t^\text{obj} xtobj分别表示当前末端执行器与物体的位姿， τ t ∈ [ 0 , 1 ] \tau_t\in[0,1] τt∈[0,1]表示归一化的时间索引， x t o \mathbf{x}t^o xto是来自生成视频的目标物体位姿。 { x grasp , d pre , x t base } \{\mathbf{x}^\text{grasp},d\text{pre},\mathbf{x}t^\text{base}\} {xgrasp,dpre,xtbase}是由抓取与规划产生的基线动作：其中， x grasp \mathbf{x}^\text{grasp} xgrasp是抓取候选， d pre d\text{pre} dpre是预抓取偏移量， x t base \mathbf{x}_t^\text{base} xtbase是时间 t t t 处规划得到的末端执行器位姿。

4. Observation space：策略到底看到了什么？（这一步最容易看懵）

他们用基于状态（state-based）而不是纯图像策略，是为了提高样本效率。

策略的观测是：

o t = [ x t ee , x t obj , τ t , x t o , x grasp , d pre , x t base ] , (6) \mathbf{o}_t= [\mathbf{x}_t^\text{ee},\mathbf{x}_t^\text{obj},\tau_t,\mathbf{x}t^o,\mathbf{x}^\text{grasp},d\text{pre},\mathbf{x}_t^\text{base}],\tag{6} ot=[xtee,xtobj,τt,xto,xgrasp,dpre,xtbase],(6)

我按"你脑子里要装的意义"解释：

4.1 当前世界状态（告诉 RL 现实现在怎样）

x t ee \mathbf{x}_t^\text{ee} xtee：末端执行器当前位姿（手当前在哪、朝向怎样）

x t obj \mathbf{x}_t^\text{obj} xtobj：物体当前位姿（物体现在在哪、朝向怎样）

4.2 时间信息（告诉 RL "现在是轨迹的第几段"）

τ t ∈ [ 0 , 1 ] \tau_t\in[0,1] τt∈[0,1]：归一化时间索引直觉：同样的误差在"开始阶段"和"结束阶段"应该采取不同修正强度/方向

4.3 目标（告诉 RL 你要追哪个"视频目标姿态"）

x t o \mathbf{x}_t^o xto：来自生成视频的目标物体位姿（监督信号）

这是 object-centric 的关键：

RL 明确知道"此刻物体应该在哪"。

4.4 基线计划（告诉 RL 规划器打算怎么做）

x grasp \mathbf{x}^\text{grasp} xgrasp：抓取候选（比如抓哪、怎么抓的方案）

d pre d_\text{pre} dpre：预抓取偏移（先到一个预抓点再接近）

x t base \mathbf{x}_t^\text{base} xtbase：规划得到的第 t 步末端位姿基线（规划器给的参考轨迹）

这三项的意义非常核心：

RL 不是蒙着眼乱动，它知道"规划器本来想让我去哪"，然后它只在这个基础上改一点点。

策略输出一个残差动作 [ Δ p t , ω t ] [\Delta \mathbf{p}_t,\omega_t] [Δpt,ωt]，其中 Δ p t ∈ R 3 \Delta \mathbf{p}_t\in\mathbb{R}^3 Δpt∈R3为平移量， ω t ∈ R 3 \omega_t\in\mathbb{R}^3 ωt∈R3为旋转量。最终执行的指令用于修正基线位姿 x t base \mathbf{x}_t^\text{base} xtbase：

p t cmd = p t base + Δ p t , q t cmd = exp ⁡ ( [ ω t ] × ) q t base , (7) \mathbf{p}_t^\text{cmd}=\mathbf{p}_t^\text{base}+\Delta \mathbf{p}_t,\quad \mathbf{q}t^\text{cmd}=\exp([\omega_t]\times)\mathbf{q}_t^\text{base},\tag{7} ptcmd=ptbase+Δpt,qtcmd=exp([ωt]×)qtbase,(7)

其中， x t base = [ p t base , q t base ] \mathbf{x}_t^\text{base}=[\mathbf{p}_t^\text{base},\mathbf{q}_t^\text{base}] xtbase=[ptbase,qtbase]， x t cmd = [ p t cmd , q t cmd ] \mathbf{x}_t^\text{cmd}=[\mathbf{p}_t^\text{cmd},\mathbf{q}_t^\text{cmd}] xtcmd=[ptcmd,qtcmd]为用于机器人控制的最终末端执行器位姿指令。

5. Action space：残差到底输出什么？（式(7)是关键）

策略输出残差动作：

Δ p t ∈ R 3 \Delta \mathbf{p}_t\in\mathbb{R}^3 Δpt∈R3：位置的微调（往哪挪一点）

ω t ∈ R 3 \omega_t\in\mathbb{R}^3 ωt∈R3：旋转的微调（绕哪个轴转一点）

然后把它们作用到基线末端位姿 x t base = [ p t base , q t base ] \mathbf{x}_t^\text{base}=[\mathbf{p}_t^\text{base},\mathbf{q}_t^\text{base}] xtbase=[ptbase,qtbase] 上：

p t cmd = p t base + Δ p t , q t cmd = exp ⁡ ( [ ω t ] × ) q t base , (7) \mathbf{p}_t^\text{cmd}=\mathbf{p}_t^\text{base}+\Delta \mathbf{p}_t,\quad \mathbf{q}t^\text{cmd}=\exp([\omega_t]\times)\mathbf{q}_t^\text{base},\tag{7} ptcmd=ptbase+Δpt,qtcmd=exp([ωt]×)qtbase,(7)

这句你最容易卡住的是旋转那项，我用"最白话"的解释：

四元数 q t base \mathbf{q}_t^\text{base} qtbase 是"基线朝向"

ω t \omega_t ωt 表示一个"小旋转"（像一个小角度的轴角向量）

exp ⁡ ( [ ω t ] × ) \exp([\omega_t]_\times) exp([ωt]×) 把"小旋转"变成一个真正的旋转（相当于 Rodrigues/指数映射）

然后用这个小旋转去"左乘"基线四元数，得到最终指令朝向

你可以把它理解成：

基线姿态是大方向，RL 给一个"小扳手"，把方向再扳准一点。

最终输出给机器人控制的是末端位姿指令 x t cmd \mathbf{x}_t^\text{cmd} xtcmd。

Rewards（奖励函数） 我们设计了能够泛化到多种任务的简单奖励函数。具体而言，物体跟踪奖励 r t trk r_t^\text{trk} rttrk 鼓励机器人将物体对齐到视频中的目标位姿：

r t trk = w pos e − k pos ∥ p t obj − p t o ∥ 2 + w ori e − k ori ∥ q t obj − q t o ∥ 2 , (8) r_t^\text{trk}=w_\text{pos}e^{-k_\text{pos}\|\mathbf{p}_t^\text{obj}-\mathbf{p}t^o\|2} +w\text{ori}e^{-k\text{ori}\|\mathbf{q}_t^\text{obj}-\mathbf{q}_t^o\|_2},\tag{8} rttrk=wpose−kpos∥ptobj−pto∥2+worie−kori∥qtobj−qto∥2,(8)

抓取奖励 r t grasp r_t^\text{grasp} rtgrasp 通过惩罚抓取或持有过程中末端执行器与物体之间的过大距离，来保证稳定抓取与运动：

r t grasp = − w grasp 1 [ ∥ p t ee − p t obj ∥ 2 > τ ] , (9) r_t^\text{grasp}=-w_\text{grasp}\,\mathbf{1}[\|\mathbf{p}_t^\text{ee} - \mathbf{p}_t^\text{obj}\|_2>\tau],\tag{9} rtgrasp=−wgrasp1[∥ptee−ptobj∥2>τ],(9)

其中， p t ee \mathbf{p}_t^\text{ee} ptee为末端执行器位置， τ \tau τ为距离阈值， 1 [ ⋅ ] \mathbf{1}[\cdot] 1[⋅]为指示函数。

规划奖励 r t plan r_t^\text{plan} rtplan 在逆运动学或运动规划失败时给予负奖励，以抑制不可行的动作。我们在物理世界模型中，利用上述奖励项训练策略 π θ ( o t ) \pi_\theta(\mathbf{o}_t) πθ(ot) ，并采用 PPO[72] 作为学习算法。利用基线动作能够显著加速收敛，因为策略只需学习残差修正。

6. Rewards：他们怎么让 RL 学会"跟随视频里的物体运动"？

他们强调"简单且可泛化"。奖励由几块组成：

6.1 物体跟踪奖励 r t trk r_t^\text{trk} rttrk：追目标位姿

r t trk = w pos e − k pos ∥ p t obj − p t o ∥ 2 + w ori e − k ori ∥ q t obj − q t o ∥ 2 , (8) r_t^\text{trk}=w_\text{pos}e^{-k_\text{pos}\|\mathbf{p}_t^\text{obj}-\mathbf{p}t^o\|2} +w\text{ori}e^{-k\text{ori}\|\mathbf{q}_t^\text{obj}-\mathbf{q}_t^o\|_2},\tag{8} rttrk=wpose−kpos∥ptobj−pto∥2+worie−kori∥qtobj−qto∥2,(8)

你要读成：

物体位置越接近目标位置 p t o \mathbf{p}t^o pto，奖励越接近 w pos w\text{pos} wpos

物体旋转越接近目标姿态 q t o \mathbf{q}t^o qto，奖励越接近 w ori w\text{ori} wori

指数形式 e − k ∣ e r r o r ∣ e^{-k|error|} e−k∣error∣ 的特点： 误差越小奖励越大，而且误差稍大时奖励会快速下降，逼你把误差压下去

注意：这里 p t obj \mathbf{p}_t^\text{obj} ptobj、 q t obj \mathbf{q}_t^\text{obj} qtobj 是物理仿真里"真实物体"的当前位姿。这就是"物理反馈"：你动了，仿真告诉你物体真的去哪了。

6.2 抓取奖励 r t grasp r_t^\text{grasp} rtgrasp：别抓丢 / 别离得太远

r t grasp = − w grasp 1 [ ∥ p t ee − p t obj ∥ 2 > τ ] , (9) r_t^\text{grasp}=-w_\text{grasp}\,\mathbf{1}[\|\mathbf{p}_t^\text{ee} - \mathbf{p}_t^\text{obj}\|_2>\tau],\tag{9} rtgrasp=−wgrasp1[∥ptee−ptobj∥2>τ],(9)

解释：

如果末端和物体距离超过阈值 τ \tau τ，说明你可能没抓稳/脱手/没跟上，就给一个固定负奖励

这是一个"硬约束式"的惩罚，让策略保持稳定接触或持有

6.3 规划奖励 r t plan r_t^\text{plan} rtplan：IK/规划失败就惩罚

这项没写公式，但意义很清楚：

如果你的残差修正导致 IK 解不出来、或规划不可行 → 给负奖励 → 让策略学会"别输出让系统崩掉的修正"

7. 用 PPO 训练：这里 PPO 扮演什么角色？

他们说用 PPO[72]。你要理解它在这里是"怎么用"的：

环境：物理世界模型（仿真）

策略： π θ ( o t ) \pi_\theta(\mathbf{o}_t) πθ(ot) 输出残差

执行：动作 = 基线 + 残差

奖励：跟踪 + 抓取 + 规划

PPO：通过与仿真反复交互，更新 θ \theta θ，让长期累积奖励最大

关键加速点不是 PPO 本身，而是：

有基线动作，PPO 学的是小范围修正 → 收敛更快。

IV. EXPERIMENTS

我们的实验旨在评估 PhysWorld 作为一个统一视频生成与物理世界建模的框架的有效性，量化其在不依赖任务特定机器人示范的情况下的泛化能力，并分析关键设计选择与局限性。为此，我们将实验组织为依次回答以下经验性问题：

（Q1）视频生成： 视频生成是否能够实现更具泛化性的机器人操作？（第 IV-A 节）

（Q2）世界建模： 物理世界建模是否能够提升操作任务中的鲁棒性？（第 IV-B 节）

（Q3）学习： 以物体为中心的残差强化学习是否相较于其他方法提升了策略效果？（第 IV-C 节）

A. Video Generation Enables Generalizable Manipulation 视频生成实现可泛化的操作

Qualitative evaluation（定性评估） 为了回答视频生成是否能够实现更具泛化性的机器人操作，我们在一组多样化的真实世界操作任务上评估了 PhysWorld，包括： 1）擦白板；2）给花浇水；3）把书放进书架；4）将锅里的鱼倒到盘子里；5）把锅盖盖到锅上；6）把勺子放进锅里；7）把鞋子放进鞋盒；8）将勺子里的糖果倒到盘子里；9）把纸屑扫进簸箕；10）将锅里的番茄倒到盘子里。 PhysWorld 在真实世界操作任务上的定性评估结果如图 5 所示。生成的、任务条件化的视频在多样化场景中提供了丰富的任务级视觉引导，而我们的物理世界模型将这些引导落地为可执行的动作，无需额外的机器人数据，从而实现真实世界中的零样本机器人操作。

Video generation quality（视频生成质量） 为了分析视频生成质量对下游操作任务的影响，我们比较了四种图像到视频生成模型： Veo3[63]、Tesseract[11]、CogVideoX1.5-5B[9] 以及 Cosmos-2B[10]，并在同一组任务上进行比较。对于每一种模型与任务的组合，我们生成 10 个视频，并计算其中可用视频的比例，即能够稳健地恢复物体位姿的视频比例。表 I 汇报了各任务上的可用视频比例。 Veo3 在整体上取得了最高的可用比例，而经过机器人数据微调的模型（如 Tesseract）通常优于通用生成模型。这些结果表明，高质量且与任务一致的视频生成对于实现可靠的机器人操作是必要的。

B. World Modeling Improves Manipulation Robustness 世界建模提升操作鲁棒性

Physical scene reconstruction quality（物理场景重建质量） 图 3 展示了从生成视频中重建得到的模型。我们的方法将几何对齐的四维重建与生成式先验相结合，从单目输入中恢复潜在的物理场景。重建得到的场景在几何上保持一致，并且可进行物理交互，从而为机器人学习提供可靠的物理反馈。

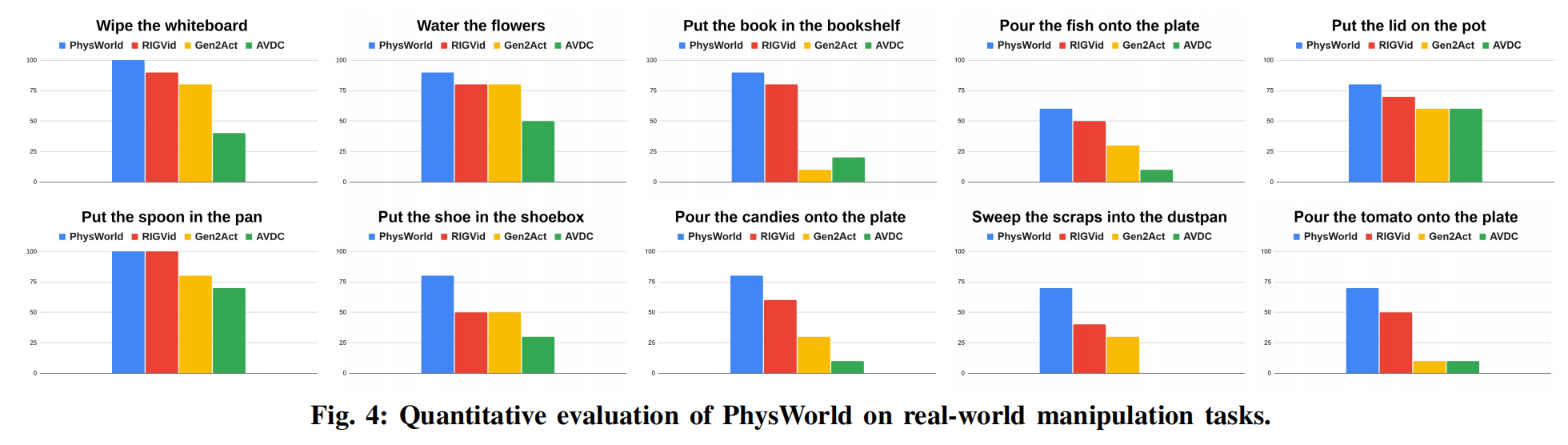
Effectiveness of world modeling（世界建模的有效性） 为评估引入物理世界模型的有效性，我们在 10 个真实世界操作任务上进行评测，每个任务运行 10 次，并汇报各任务的成功率。我们将本方法与三种不使用物理世界建模的零样本方法进行比较：（i）RIGVid[8]：直接从生成视频中跟踪物体位姿，并利用现成的抓取模型与运动规划进行机器人控制；（ii）Gen2Act[7]：我们采用[8]中的修改版本，以稀疏点轨迹作为跟踪目标；（iii）AVDC[6]：利用深度与光流估计来表征物体和具身运动。图 4 总结了定量对比结果： PhysWorld 取得了最高的平均成功率（82%），显著优于第二名方法[8]（67%）。这表明，从物理世界模型中学习能够提供纠错性的反馈，从而减少抓取与规划过程中误差的累积，尤其是在抓取、插入和倾倒等阶段。此外，以物体位姿作为跟踪目标显著优于使用点轨迹[7]和光流[6]的方法。这表明，相比点轨迹和光流，物体位姿估计能够从生成视频中提供更加鲁棒的物体运动信号，而前两者在遮挡和运动模糊下常会发生漂移。

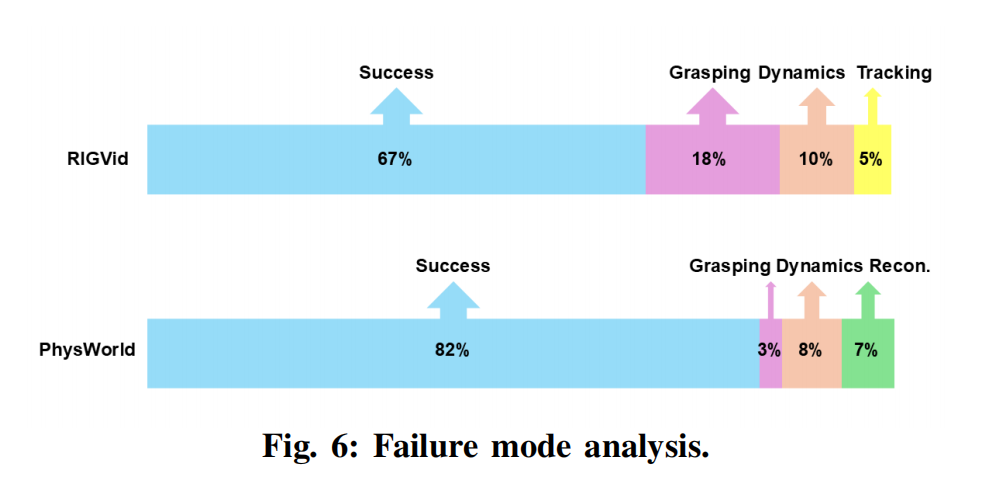
Failure mode analysis（失败模式分析） 为进一步分析性能提升的来源，图 6 将失败案例划分为四类：抓取、跟踪、动力学以及重建。与[8]相比，引入物理世界模型将抓取失败率从 18% 显著降低到 3%，并将跟踪失败从 5% 降至 0%，表明物理世界模型提供的物理反馈至关重要。我们的方法引入了 7% 的重建误差。这主要是由于我们从单目生成视频中重建物理场景，被遮挡区域补全的几何可能与真实世界几何不完全对齐。然而，我们认为可以通过事先对环境进行多视角重建来缓解这一问题。

C. Object-Centric Learning Enhances Policy Effectiveness 以物体为中心的学习提升策略有效性

Object-centric vs. embodiment-centric learning（以物体为中心 vs. 以具身为中心的学习） 我们比较了两种从视频中学习的范式：（i）以具身为中心的学习：重建人手网格，并将手指关键点映射为机器人末端执行器的运动轨迹；（ii）以物体为中心的学习：训练策略去跟随物体的运动。如表 II 所示，以物体为中心的学习显著更强（"把书放进书架"：90% 对 30%；"把鞋子放进鞋盒"：80% 对 10%）。其主要原因在于生成视频中常常会虚构人手，或呈现不一致的手部运动学，而物体运动更加稳定，并且在遮挡条件下更易估计。因此，以物体为中心的学习能够更可靠地迁移到机器人上，并且与我们的物理约束训练更加契合。

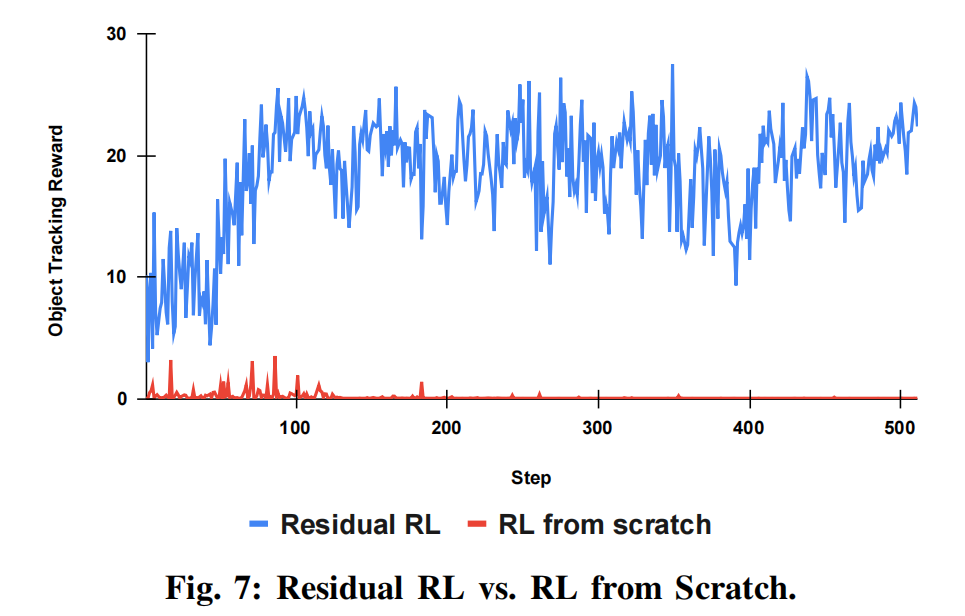
Residual RL vs. RL from scratch （残差强化学习 vs. 从零开始的强化学习） 我们进一步在相同的物理世界模型下、以"将锅里的番茄倒到盘子里"任务为例，对比了残差强化学习与从零开始训练策略的方法（见图 7）。残差强化学习在数百次迭代内即可收敛，并在相同训练预算下获得更高的物体跟踪奖励。基线的抓取与规划动作将探索限制在一个较小且可行的邻域内，而物理世界模型提供的纠错反馈则被残差策略用来细化运动轨迹。相比之下，从零开始的强化学习也可以成功[17]，但需要更长的训练时间以及更加精心设计的奖励函数。因此，结合物理世界模型的残差强化学习能够实现更快的学习速度，并提升操作的鲁棒性。

V. CONCLUSION

我们提出了 PhysWorld，这是一个通过物理世界建模将视频生成与机器人学习连接起来的框架。 PhysWorld 通过从生成视频中重建可进行物理交互的场景，并学习以物体为中心的残差强化学习策略，将生成的视觉示范转化为物理上可行的机器人动作，从而在真实世界实现零样本、可泛化的操作。未来工作包括利用该框架合成物理上准确的视频，用于训练面向机器人的视频生成模型。

Limitations. 局限性 物理世界建模受限于物理仿真器的逼真度，并可能引入额外的仿真到现实（sim-to-real）差距。然而，根据图 4 的证据，我们仍然认为引入世界模型是必要的，因为它能提供可靠的物理反馈，从而实现更鲁棒的学习。