文章目录
-
- 一、逻辑回归简介
- 二、逻辑回归的原理
-
- [1. Sigmoid函数](#1. Sigmoid函数)
- [2. 决策边界](#2. 决策边界)
- [3. 损失函数](#3. 损失函数)
- 三、逻辑回归的优势与局限
- 四、示例:银行数据训练
-
- [1. 数据准备与探索](#1. 数据准备与探索)
- [2. 特征选择与数据划分](#2. 特征选择与数据划分)
- [3. 模型训练与评估](#3. 模型训练与评估)
一、逻辑回归简介
逻辑回归(Logistic Regression)是一种广泛应用于分类问题的统计学习方法,尤其擅长处理二分类问题。尽管名字中带有"回归",但它实际上是一种分类算法。逻辑回归通过Sigmoid函数将线性回归的输出映射到(0,1)区间,从而得到样本属于某一类别的概率。
二、逻辑回归的原理
1. Sigmoid函数
逻辑回归的核心是Sigmoid函数(也称为逻辑函数):
P ( y = 1 ∣ x ) = 1 1 + e − z P(y=1|x) = \frac{1}{1 + e^{-z}} P(y=1∣x)=1+e−z1
其中z是输入特征的线性组合: z = w 0 + w 1 x 1 + w 2 x 2 + . . . + w n x n z = w₀ + w₁x₁ + w₂x₂ + ... + wₙxₙ z=w0+w1x1+w2x2+...+wnxn
2. 决策边界
当 P ( y = 1 ∣ x ) ≥ 0.5 P(y=1|x) ≥ 0.5 P(y=1∣x)≥0.5时,模型预测为正类;当 P ( y = 1 ∣ x ) < 0.5 P(y=1|x) < 0.5 P(y=1∣x)<0.5时,预测为负类。0.5这个阈值形成了决策边界。
3. 损失函数
逻辑回归使用交叉熵损失函数(对数损失函数),通过最大似然估计或梯度下降等优化方法寻找最优参数。
三、逻辑回归的优势与局限
优势:
- 计算效率高,训练和预测速度快
- 输出具有概率意义,可解释性强
- 对线性可分或近似线性可分的数据表现良好
- 不容易过拟合,尤其适合高维数据
局限:
- 对非线性决策边界的数据效果有限
- 对多重共线性敏感
- 需要较大的样本量来保证参数估计的稳定性
四、示例:银行数据训练
1. 数据准备与探索
python
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
import pandas as pd
import matplotlib.pyplot as plt
from pylab import mpl
from sklearn.linear_model import LogisticRegression
from sklearn import metrics
# 读取数据并进行预处理
data = pd.read_csv(r"creditcard.csv")
scaler = StandardScaler()
data["Amount"] = scaler.fit_transform(data[["Amount"]])
data = data.drop(["Time"], axis=1)
# 设置中文字体支持
mpl.rcParams["font.sans-serif"] = ["Microsoft YaHei"]
mpl.rcParams["axes.unicode_minus"] = False
# 查看正负例样本分布
labels_count = pd.value_counts(data["Class"])
print(labels_count)
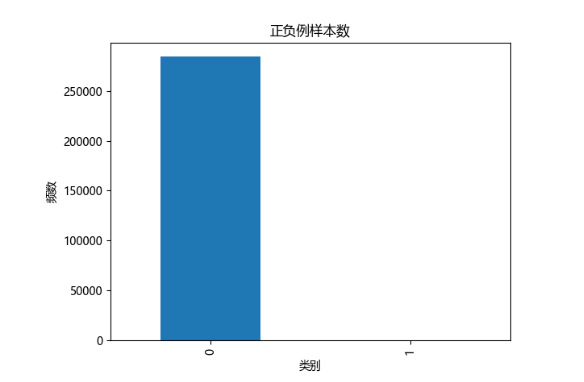
# 可视化样本分布
plt.title("正负例样本数")
plt.xlabel("类别")
plt.ylabel("频数")
labels_count.plot(kind='bar')
plt.show()
2. 特征选择与数据划分
python
# 选择特征列
column_names = ['V1', 'V2', 'V3', 'V4', 'V5', 'V6', 'V7', 'V8', 'V9', 'V10',
'V11', 'V12', 'V13', 'V14', 'V15', 'V16', 'V17', 'V18', 'V19',
'V20', 'V21', 'V22', 'V23', 'V24', 'V25', 'V26', 'V27', 'V28', 'Amount']
x_whole = data[column_names]
y_whole = data[["Class"]]
# 划分训练集和测试集(这里使用30%作为训练集)
x_train_w, x_test_w, y_train_w, y_test_w = train_test_split(x_whole, y_whole, train_size=0.3, random_state=1000)3. 模型训练与评估
python
# 创建并训练逻辑回归模型
# C参数是正则化强度的倒数,较小的C值表示更强的正则化
lr = LogisticRegression(C = 0.01)
lr.fit(x_train_w, y_train_w)
# 在测试集上进行预测
test_predicted = lr.predict(x_test_w)
result = lr.score(x_test_w,y_test_w)
# 输出详细的分类报告
print(metrics.classification_report(y_test_w, test_predicted))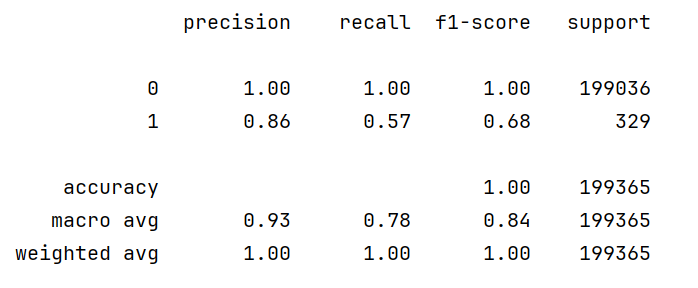
图中包含以下关键指标:
- 精确率(Precision):预测为正例的样本中实际为正例的比例
- 召回率(Recall):实际为正例的样本中被正确预测的比例
- F1-score:精确率和召回率的调和平均数
- 准确率(Accuracy):所有样本中被正确分类的比例