leetcode热题路径总和 III

给定一个二叉树的根节点 root ，和一个整数 targetSum ，求该二叉树里节点值之和等于 targetSum 的路径的数目。

路径不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。

示例 1：

复制代码

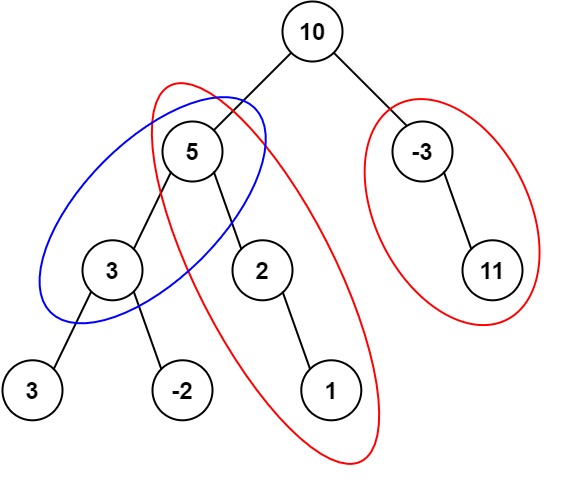
输入：root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
输出：3
解释：和等于 8 的路径有 3 条，如图所示。

java 复制代码

    public int pathSum(TreeNode root, long targetSum) {
        if (root == null) {
            return 0;
        }
        int count = rootSum(root, targetSum);
        count += pathSum(root.left,targetSum);
        count += pathSum(root.right,targetSum);
        return count;

    }

    private int rootSum(TreeNode root, long targetSum) {
        int ret = 0;
        if (root == null) {
            return ret;
        }
        int val = root.val;
        if (val == targetSum) {
            ret++;
        }
        ret += rootSum(root.left, targetSum - val);
        ret += rootSum(root.right, targetSum -val);
        return ret;
    }


    // 前辍和
    public int pathSum1(TreeNode root, long targetSum) {
        Map<Long, Integer> prefix = new HashMap<>();
        prefix.put(0L,1);
        return rootDfs(root,prefix,0,targetSum);

    }



    /**
     *
     * @param root
     * @param prefix
     * @param curr
     * @param targetSum
     * @return
     * des  先序遍历递归，往map里不断放入当前节点到根节点的和，并不断从map里取出前辍和是否等于当前节点和-targetSum,如有则找到一条，当我们退出当前节点时，
     * 我们需要及时更新已经保存的前辍和，如果不更新，后续其他分支的前辍和可能一样，就导致了重复计算
     */
    private int rootDfs(TreeNode root, Map<Long, Integer> prefix, long curr, long targetSum) {
        int ret = 0;
        if (root == null) {
            return ret;
        }
        curr += root.val;
        ret = prefix.getOrDefault(curr - targetSum, 0);
        ret += rootDfs(root.left, prefix, curr, targetSum);
        ret += rootDfs(root.right, prefix, curr, targetSum);
        prefix.put(curr, prefix.getOrDefault(curr, 0) - 1);
        return ret;
    }