【算法】双指针

一、移动零

[1. 分析解答](#1. 分析解答)

[2. 代码实现](#2. 代码实现)

二、复写零

[1. 分析解答](#1. 分析解答)

[2. 代码实现](#2. 代码实现)

三、快乐数

[1. 分析解答](#1. 分析解答)

[2. 代码实现](#2. 代码实现)

四、盛最多水的容器

[1. 分析解答](#1. 分析解答)

[2. 代码实现](#2. 代码实现)

五、有效三角形的个数

[1. 分析解答](#1. 分析解答)

[2. 代码实现](#2. 代码实现)

六、查找总价格为目标值的两个商品

[1. 分析解答](#1. 分析解答)

[2. 代码实现](#2. 代码实现)

七、三数之和

[1. 分析解答](#1. 分析解答)

[2. 代码实现](#2. 代码实现)

八、四数之和

[1. 分析解决](#1. 分析解决)

[2. 代码实现](#2. 代码实现)

前言

本文是一篇关于对双指针进行学习使用的一篇算文章。将会从以下几个题型进行分析我们对双指针算法的使用情况。进而更加理解双指针。

一、移动零

原题目链接：283. 移动零 - 力扣（LeetCode）

题目：

1. 分析解答

题目的意思要求有如下几点：

先给定一个数组，将数组的为0的所有元素全部都移动到数组的末尾。

需要保证移动后其余非零元素的先后顺序需要与原数组一致。

必须在不复制数组的情况下原地对数组进行操作，也就是不能定义新的数组通过拷贝的方法解决。

如上图，示例也给出来了：数组：[0,1,0,3,12] 移动后需要变成 [1,3,12,0,0] 。

解决这个问题我们需要将数组划分，也就是数组分块的思想。我们最终需要将数组划分为一遍是非零区间部分，一遍为零区间部分，即：

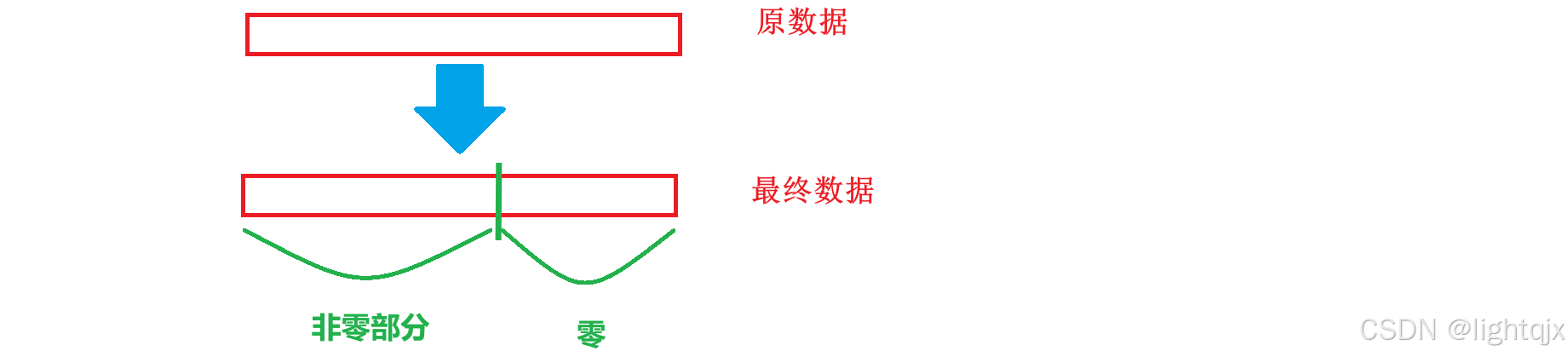
为了达到这个目的，我们就可以从左往右遍历数组，逐步处理数组，也就是将数组可以划分为处理了的区域和未处理区域，其中对于处理了的区域又可以分为非零区和为零区。即：

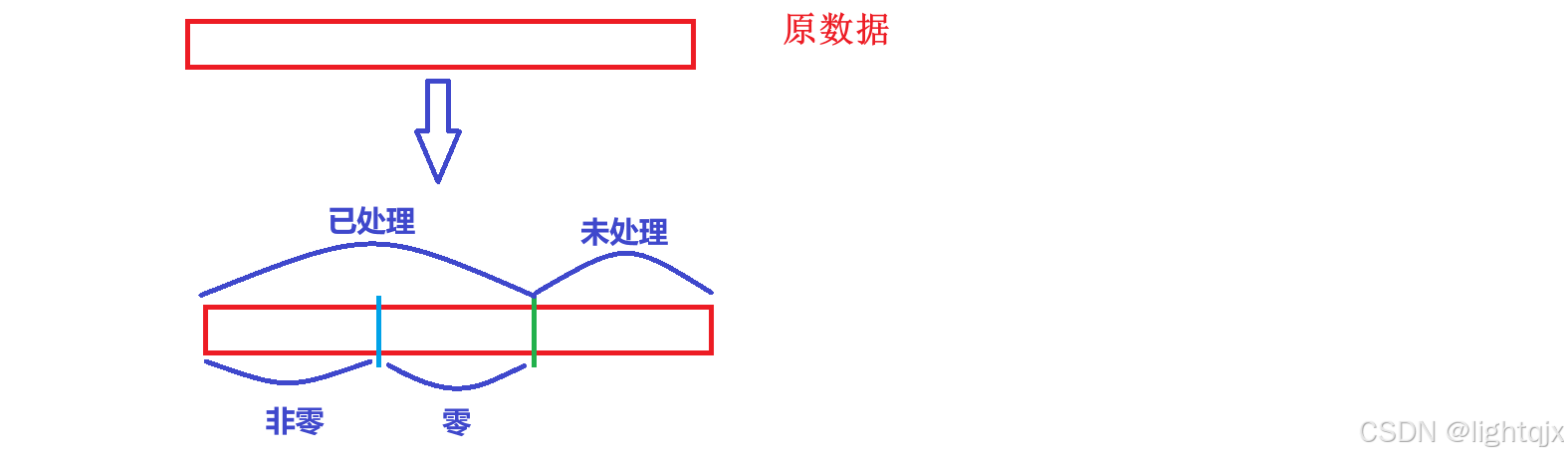
这是我们就可以使用双指针的解决思想了。使用两个**"指针"** ：cur和prev。在数组中我们这里的指针并不是正真的表示地址的指针，而是通过将下标作为访问的指针的，因为这样访问比较方便。

cur：用来从左往右遍历数组，指向我们遍历的当前位置，即未处理区域的第一个位置。

prev：指向我们已处理区域的最后一个非零元素。

这是我们数组就可以分成三个区间：非零区[ 0，prev ]，为零区[ prev+1,cur-1 ]，未处理区[ cur，numSize-1 ] 。

初始时 数组都处于未处理状态，此时cur就指向第一个元素，prev是处理区里的最后一个非零元素，所以这时prev就指向第一个元素的前一个位置：

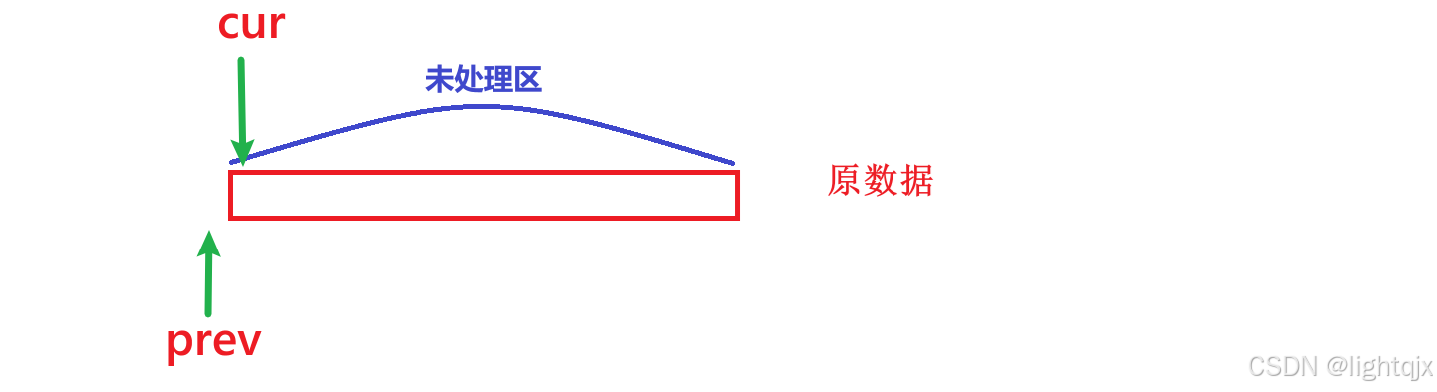
我们要做到将处理区分为非零区个为零区，可以这样做到：

cur在从前往后遍历的过程中：

如果cur遇到0，就只将cur++；

如果cur遇到非零元素，就需要将prev+1指的元素（第一个为零区的第一个元素）与cur指向的元素（未处理区的第一个非零元素）进行交换。再将cur和prev都分别++。

如此就可以将未处理区的非零元素不断更新到已处理区的非零区的最后面，既能让0不断后移，也能让所有未处理区的非零元素不断按照当前非零元素顺序插入到处理区的非零区。

2. 代码实现

对于代码的实现我们并不局限于语言，只要掌握算法思路，任何语言都可以写出来。这里我采用C++语言来写：

cpp 复制代码

class Solution {
public:
    void moveZeroes(vector<int>& nums) {
        int cur=0;
        int prev=-1;
        while(cur<nums.size())
        {
            if(nums[cur]==0)
            {
                cur++;
            }
            else
            {
                swap(nums[prev+1],nums[cur]);
                prev++;
                cur++;
            }
        }
    }
};

二、复写零

原题目链接：1089. 复写零 - 力扣（LeetCode）

题目：

1. 分析解答

以示例1为例：

如果是异地操作 ：先开辟一个与原数组大小相同的新数组，然后当我们从左往右遍历[1,0,2,3,0,4,5,0]，当遇到非零数据时，就将该数据抄到新数组中去；当遇到零时，就将该数据抄两遍到新数组中去。重复此过程直到新数组满了就停止。如图所示：

而我们题目要求的是就地操作，即在原数组上进行修改。

对于这道题，我们也是采用双指针算法。

首先思考一下就地从前往后遍历复写。

先定义两个指针（即下标）cur和dest。cur首先指向第一个元素，用来遍历；dest指向第一个元素的全一个位置即-1，用来从前往后配合cur指向的元素是否为0，来进行复写。

首先判断cur的位置是否为0，

若不为0，则将dest移动一位，并在该位置抄一遍cur位置的元素，最后将cur移动到下一位；

若为0，则将dest先移动一位，并在该位置抄一遍0，将dest再移动一位，再当前该位置抄一遍0，最后将cur移动到下一位；

但是这样就会出现一些问题 ：即我们通过dest覆盖的数据可能是我们下一次要抄的值，这时cur移动下一位后，cur指向的位置仍然是我们上一次复写过了的值，那么这里被覆盖了的元素（即下一次要复写的元素）就找不到了，就会出现问题。

所以我们就不能直接就从前往后使用双指针。

那么我们就来思考从后往前使用双指针。要从后往前，就需要知道最后一个位置复写的是什么元素。通过上面我们的异地操作，就可以知道示例1的最后一个元素为4，所以此时的初始状态如下：

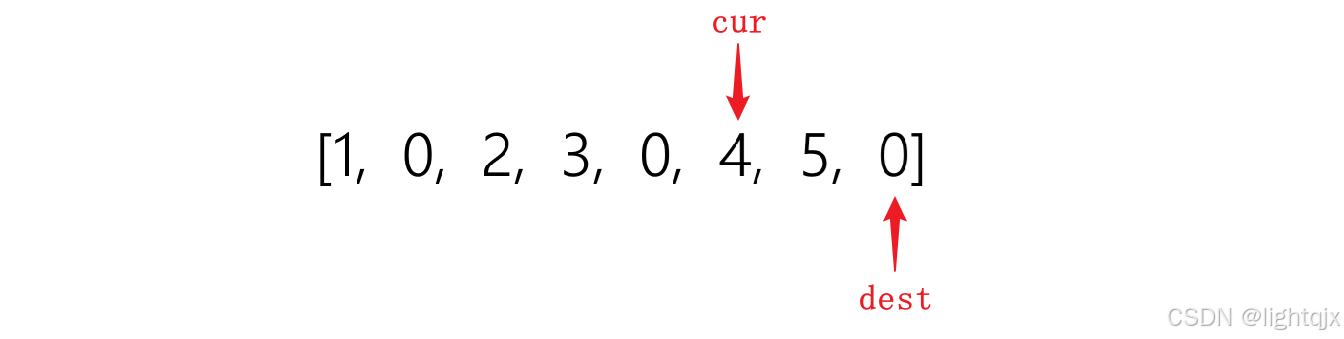
从后往前的过程如下：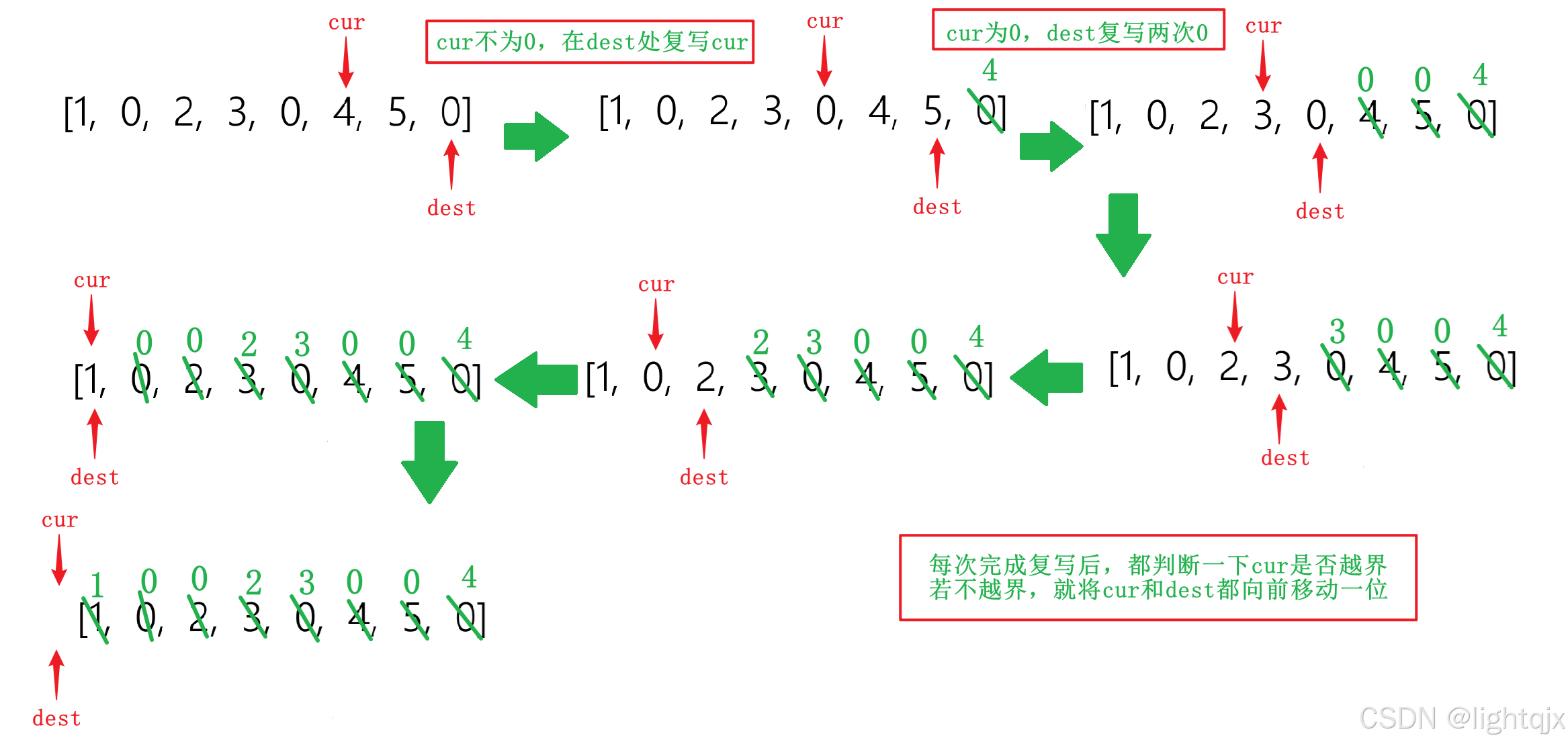

这样是可以达到目的的。

因此我们的解题思路就出来了：先使用一个双指针从前往后遍历，知道最后一个复写元素位置；然后再使用一个双指针从最后一个复写元素位置往前遍历复写。就可以达到最终目的。

主步骤1：找到最后一个复写元素位置。（第一个双指针）

初始时cur1指向第一个元素，dest指向第一个元素的前一个位置

重复这个两个步骤：

判断cur是否为0，

若cur为0，则dest移动1步

若cur不为0，dest移动2步

判断dest是否到结尾了

若没有，则cur++

若结尾了，则停止。

主步骤2：从后往前进行复写。（第二个双指针）

初始时cur指向原数组中的最后一个复写元素位置，dest指向最后一个位置。

然后重复以下几个步骤：

判断cur是否为0，

若cur为0，则先将dest所在位置复写为0，再在向前移动一位，再在该位置也复写一个0。最后将dest和cur同时向前移动一位。

若cur不为0，dest只在当前位置复写cur所在的元素，完成复写后将dest和cur同时向前移动一位

判断cur是否越界，即cur是否小于 0

若没有，则说明还没有复写完，需要继续复写，即继续判断cur所在位置。

若cur小于0，则说明复写完了，就停止程序。

其中还有一个细节问题；

比如当我们在找数组 [ 1,0,2,3,0,4 ] 的最后一个复写位置时，会出现如下情况：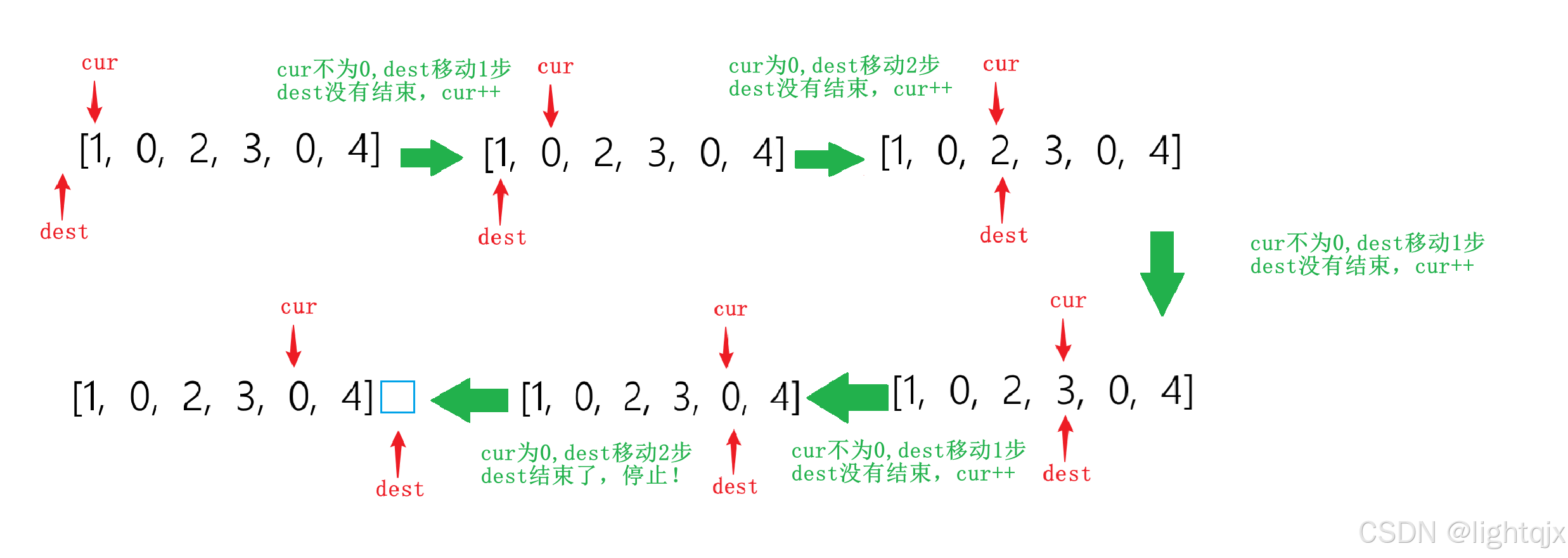

这时的dest指向的位置就是数组外了，在进行从后往前进行复写时就会出现数组越界的问题。

所以我们在进主步骤2之前就需要进行一个修正，即在1-2中间加一个中间细节步骤：处理dest越界情况：

因为dest越界情况是因为cur为0时才出现的，所以我们就只需要将数组最后一位改为0，再将cur向前移动一位，dest向前移动两位就可以正常复写了：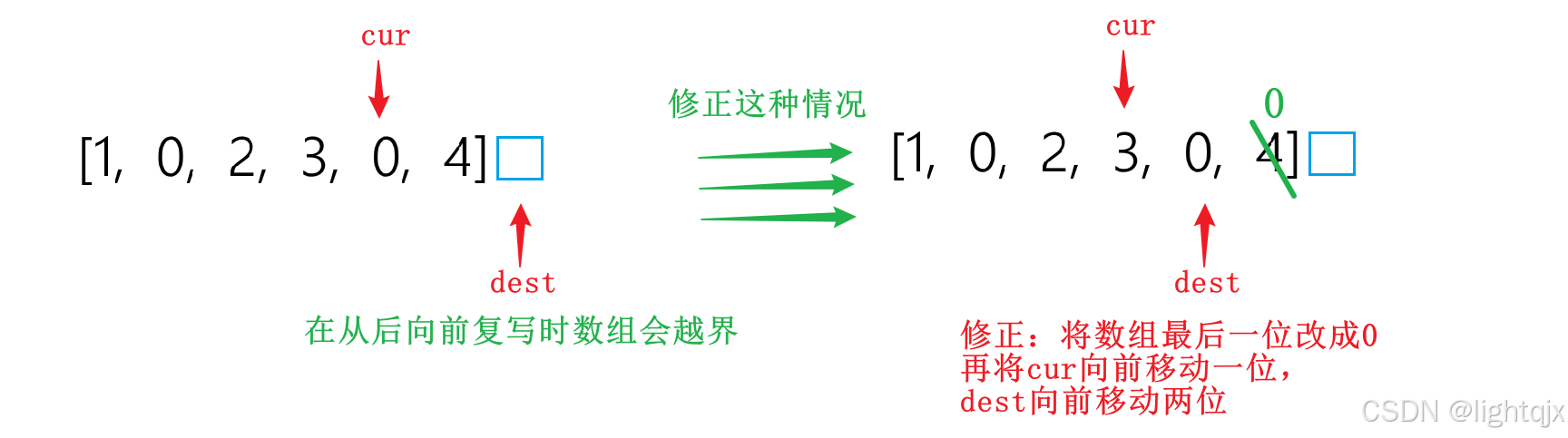

2. 代码实现

C++代码实现：

cpp 复制代码

class Solution {
public:
    void duplicateZeros(vector<int>& arr) {
        //1.找最后一个复写位置
        int cur=0,dest=-1,n=arr.size();
        while(dest<n)
        {
            if(arr[cur]) dest++; //cur不为0，dest就加1
            else dest+=2; //cur为0，dest就加2
            if(dest>=n-1) break; //判断是否到结尾
            cur++;
        }
        //2.处理边界情况
        if(dest==n)
        {
            arr[n-1]=0;
            cur--;
            dest-=2;
        }
        //3.从后往前进行复写
        while(cur>=0)
        {
            if(arr[cur]) arr[dest--]=arr[cur--];
            else
            {
                arr[dest--]=0;
                arr[dest--]=0;
                cur--;
            }
        }
    }
};

三、快乐数

题目链接：202. 快乐数 - 力扣（LeetCode）

1. 分析解答

按照题目的意思，就是每一次就将该数，换为它的各个位上的平方和。比如上面两个示例：示例1：每一次将该数替换为它每个位置上的数字的平方和，重复这个过程直到这个数变为 1才停止，因为到1后，1再变还是1,。如图所示：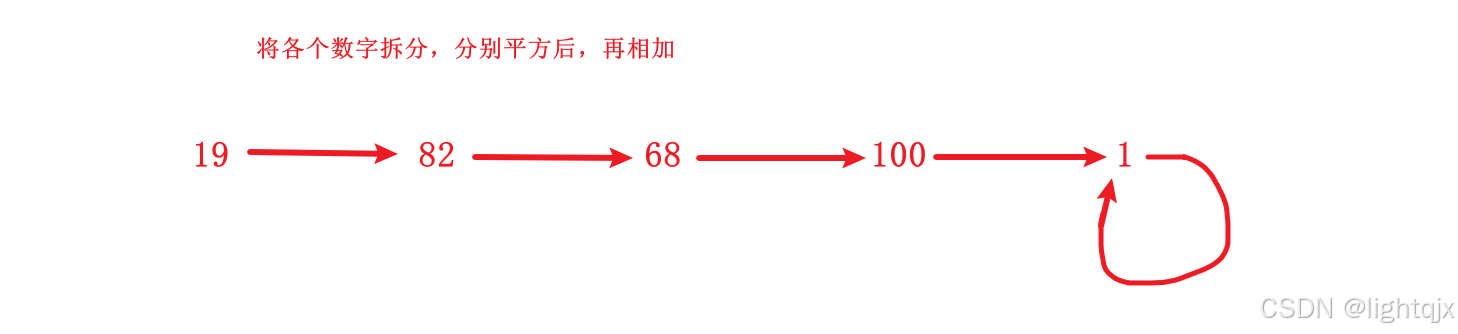

也有失败的情况是 无限循环 但始终变不到 1，这就不是快乐数。如图所示：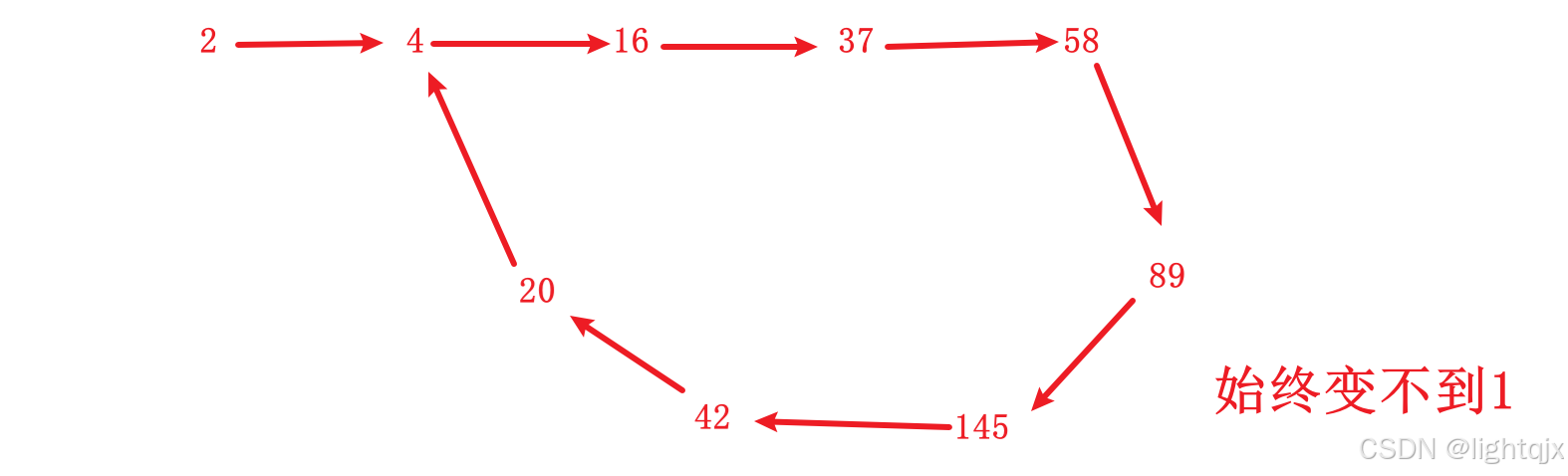

注意：通过变化能出现的只有这两种情况，不会出现一直变化没有环的情况。

解决办法

所以我们就判断最终变换后是不是1，若是1，则就是快乐数；若不是1，则不是快乐数。

注意：这里的快慢指针一定会相遇，即一定有环。

这道题是通过快慢双指针解决：定义慢指针：slow，定义快指针：fast。这里的双指针实际指的就是这个数变化成的值。通过判断快慢指针相遇时是不是1就可以解决这个问题。即：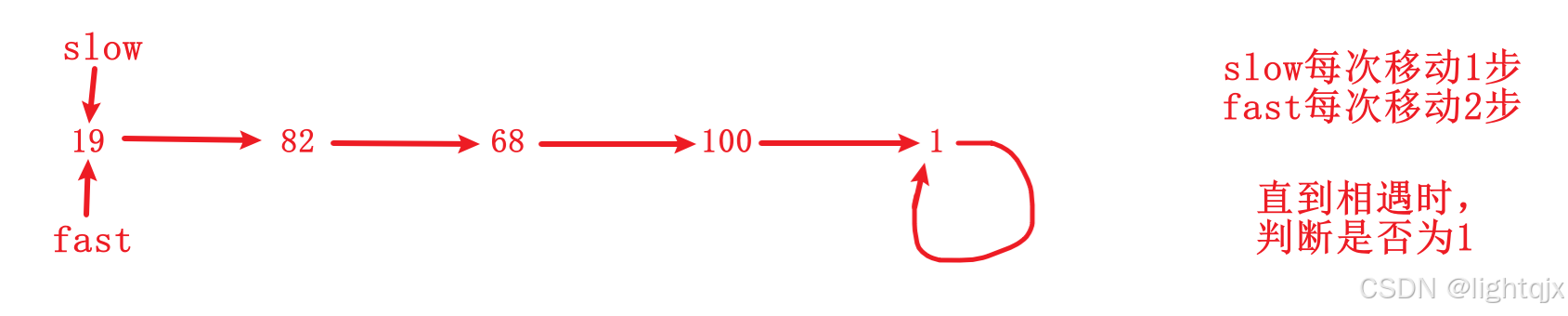

所以解题思路就是：

定义快慢指针

然后每次慢指针移动1步；快指针移动2步（这里的移动1步是指计算1次平方和）

最后判断相遇时的值是否为1.

2. 代码实现

C++代码实现如下：

cpp 复制代码

class Solution {
public:
    int GetSum(int n)
    {
        int sum=0;
        while(n)
        {
            int t=n%10; //取最后一个位数
            sum+=t*t; //加上平方和
            n/=10; // 去除当前这一位置
        }
        return sum;
    }
    bool isHappy(int n) {
        int slow=n,fast=GetSum(n);
        while(slow!=fast)
        {
            slow=GetSum(slow); //移动一步

            fast=GetSum(fast);//移动两步
            fast=GetSum(fast);
        }
        if(slow==1) return true;
        return false;
    }
};

四、盛最多水的容器

题目链接：11. 盛最多水的容器 - 力扣（LeetCode）

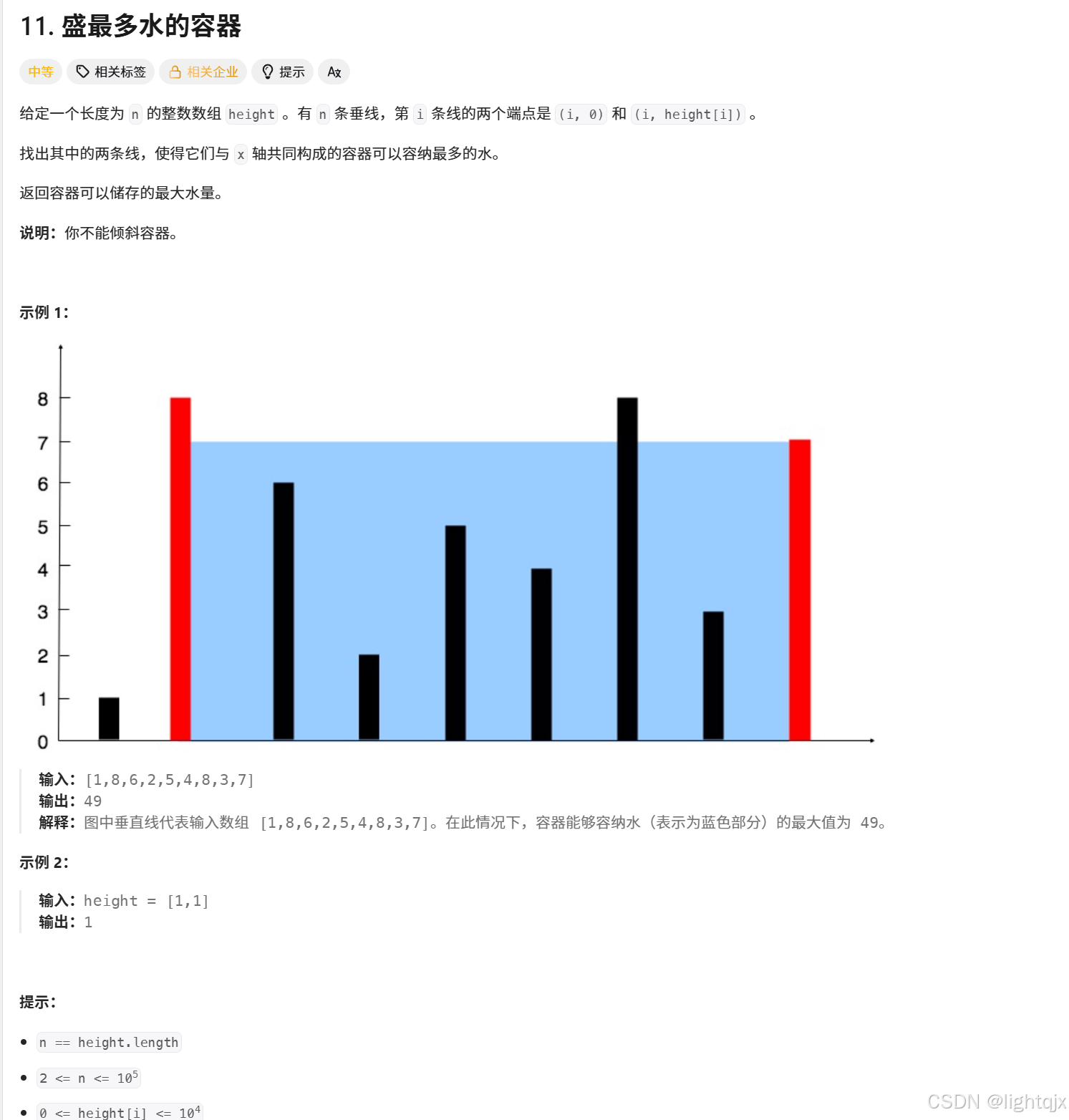
1. 分析解答

题目的意思是在给定的一个数组中去求 体积 V = 底（两点下标之差）x 高（两点下标对应数组的较小值） ，所求所有体积的最大值。

要解决这个问题，我们首先想到的就是暴力解法：通过双重遍历分别得到这里的底和高，算出所有组合的面积，在这所有的所求的面积中求的最大值就是所求答案。但是这种方法会超时。

这里我们就可以使用双指针的算法来求解这道题。我们来分析双指针算法的思路：

以[6,2,5,4]为例，我们来看看固定两个值后，移动值后的体积变化。如图所示：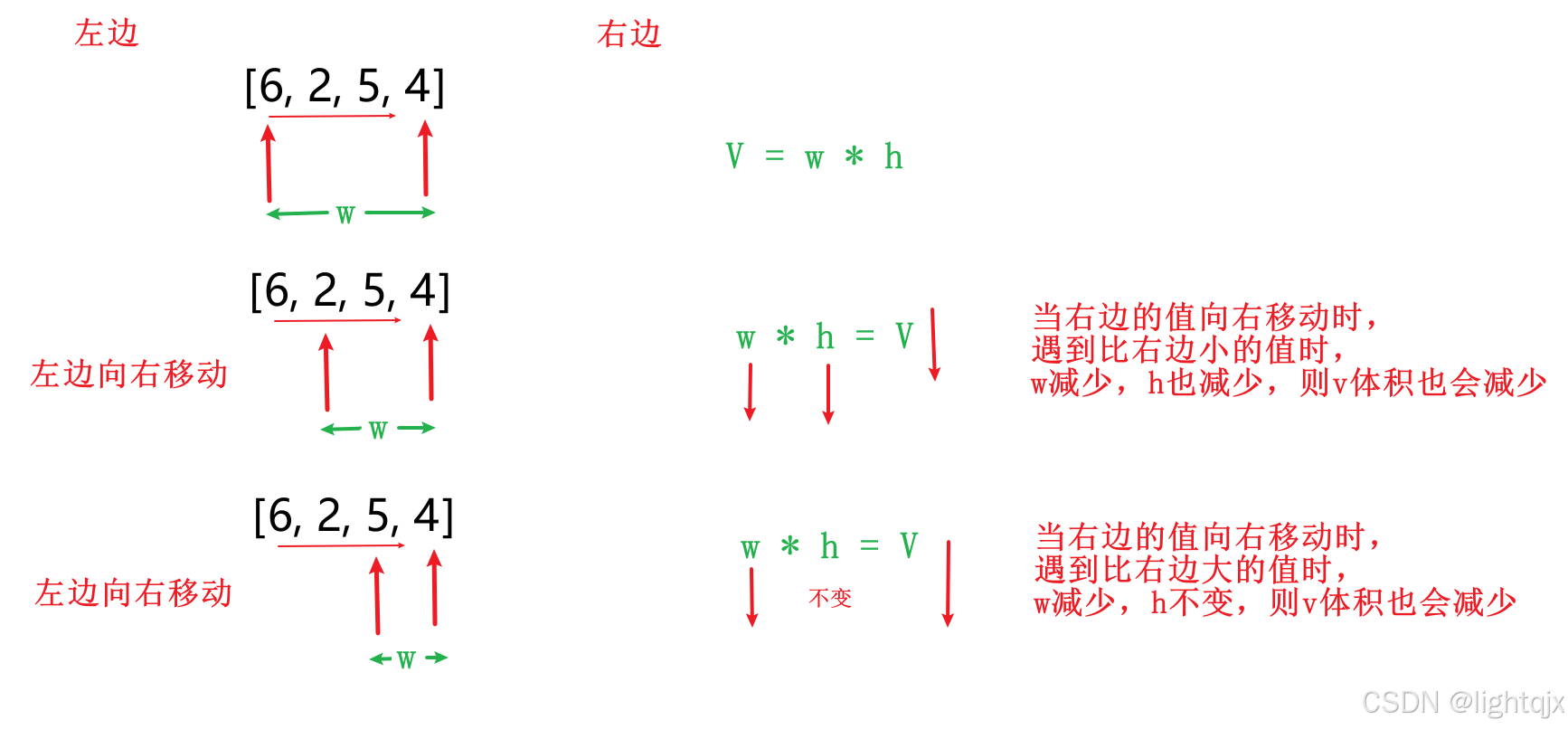

通过这里的变化，我们就可以知道，当我们固定较小的值时，另一个值向该值移动，如果遇到比所固定的值小或者大的值时，体积都会减少，所以，当前这个较小值与中间所有的值组合时，它们的值都比初始的时候要小，而我们要求较大的体积，所以我们就不能再取这个较小的值了。

因此，当我们将左边的值定为left，右边的值定为right时。

我们就不能移动值较大的一方，因为，如果我们移动值较大第一方，那么此时得到体积就一定会减小；
但是如果我们移动值较小的一方，那么当遇到比上一值大的一方时，那么我们的体积就说不定了（因为此时虽然底w变小了，但高 h 却变大了），这是计算的体积就有效。

所以，我们就可以通过统计上面通过双指针得到的这些体积中的最大值，就可以得到答案了。

那么我们的思路就可以总结如下：

当我们先将最左边的值下标定为left，最右边的值下标定为right。然后算出当前的体积，

然后将左右指针对应的值中的较小值的下标向中间移动。

在算出当前的体积。

重复2、3步，直到左右指针相遇。

最后算出所有得到的体积中的最大值就是所需结果。

2. 代码实现

按照上面的思路，我们可以在优化一下，就是边计算，边算体积最大值。

所以，C++代码实现如下：

cpp 复制代码

class Solution 
{
public:
    int maxArea(vector<int>& height) 
    {
        int max=0,left=0,right=height.size()-1;
        while(left<right)
        {
            int V=min(height[left],height[right])*(right-left);
            if(V>max) max=V;
            height[left]>height[right]?right--:left++;
        }
        return max;
    }
};

五、有效三角形的个数

题目链接：611. 有效三角形的个数 - 力扣（LeetCode）

1. 分析解答

题目的意思就是让我们在一个数组中找出可以过程三角形的组合个数。

首先我们想到的就是暴力解法：通过三次for循环来得到三条边长，再判断是否可以构成三角形。但是这种方法在题目中是会超时的。时间复杂度为。

那么我们就来使用双指针的算法思想来解决。

首先我们知道要构成三角形，就必须满足任意两条边大于第三边，其实也就是较小的两条边大于最大的那一条边就可以了。因为：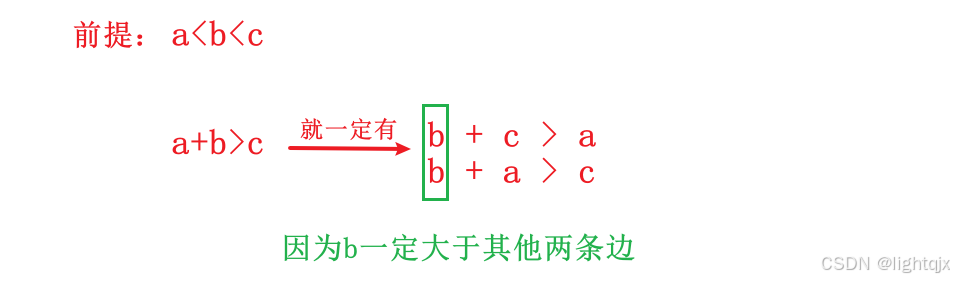

那么我们就可也这样做：先排一个升序（排序）。然后先固定一个最大值，在利用双指针来解决这道题。

这时我们再来分析：

所以，我们的思路就出来了。

先排序

再固定最大值d

再在前面的区间中定义双指针left和right

判断nums[left]+nums[right]的值

如果nums[left]+nums[right]>d，则三角形个数就加上 right - left ，再将right--

如果nums[left]+nums[right]<=d，则三角形个数就只讲left++

当双指针相遇时，再将固定的值是向前移动，再次重复上述操作，直到所固定的值是前面三个值。

时间复杂度为。

2. 代码实现

C++代码实现：

cpp 复制代码

class Solution {
public:
    int triangleNumber(vector<int>& nums) {
        //排序
        sort(nums.begin(),nums.end());

        //双指针算法思路
        int sum=0;
        for(int i=nums.size()-1;i>=2;i--)
        {
            int left=0,right=i-1;
            while(left<right)
            {
                if(nums[left]+nums[right]>nums[i])
                {
                    //构成三角形
                    sum+=right-left;
                    right--;
                }
                else
                {
                    //无法构成三角形
                    left++;
                }
            }
        }
        return sum;
    }
};

六、查找总价格为目标值的两个商品

题目链接：LCR 179. 查找总价格为目标值的两个商品 - 力扣（LeetCode）

1. 分析解答

根据题目我们知道原数组是有序的，目的相当于就是让我们在数组中找两个数等于target。

首先，我们可以使用暴力解法：使用两个for循环解决。但是这是会超时的，因为暴力解法是没有考虑到原数组有序的条件。

下面我们来实现双指针的解法：

因为我们的原数组是有序的。所以我们就可以将左边的值标为left，最有边的值标为right。通过判断条件来移动双指针，从而找到等于target的两个值。

实现思路如下：

定义left和right

如果price[left]+price[right]<target，则left++

如果price[left]+price[right]>target，则right--

重复上述操作直到price[left]+price[right]==target，才相遇。

如图所示：

2. 代码实现

C++代码实现如下：

cpp 复制代码

class Solution {
public:
    vector<int> twoSum(vector<int>& price, int target) {
        int left=0,right=price.size()-1;
        while(left<right)
        {
            int sum=price[left]+price[right];
            if(sum<target) left++;
            else if(sum>target) right--;
            else
            {
                return {price[left],price[right]};//C++11的列表初始化语法
            }
        }
         //这里是为了保证所有路径都有返回值（随便返回什么都可以）。
         //题目的意思其实是一定会有返回值的
        return {0,0};
    }
};

七、三数之和

题目链接：15. 三数之和 - 力扣（LeetCode）

1. 分析解答

题目的意思，简而言之就是在一个组数据中找到所有三个一组的数据，要求这个三个数据的下标不同，且这三个数据的和等于0。

注意细节：输出的顺序和三元组的顺序并不重要，即不用管。

要解决这个问题：

解法一：先利用排序，再暴力枚举三个不同下标对应的数，最后需要对所有组与组之间进行去重就是最后的答案，最后再来去重。但这种方法效率不高，其时间复杂度为。

解法二：利用双指针进行求解。方法就是先对原数组排序（为了方便去重），然后先固定一个数，再通过双指针枚举其他的数，枚举完了之后在移动所固定的数，重复操作。这样的时间复杂度是。

上述双指针的解法描述是我们大致的思路。其中我们还需要注意：我们需要保证所得的数据不重复，所以在遍历的时候，我们在遇到相同的数据的时候就可以跳过了。这里我们有三处地方需要跳过：1. 遍历的固定的数；2. 使用双指针遍历后续的数据时的left对应数据；3. 使用双指针遍历后续的数据时的right对应数据。

双指针的解法的详细图示如下：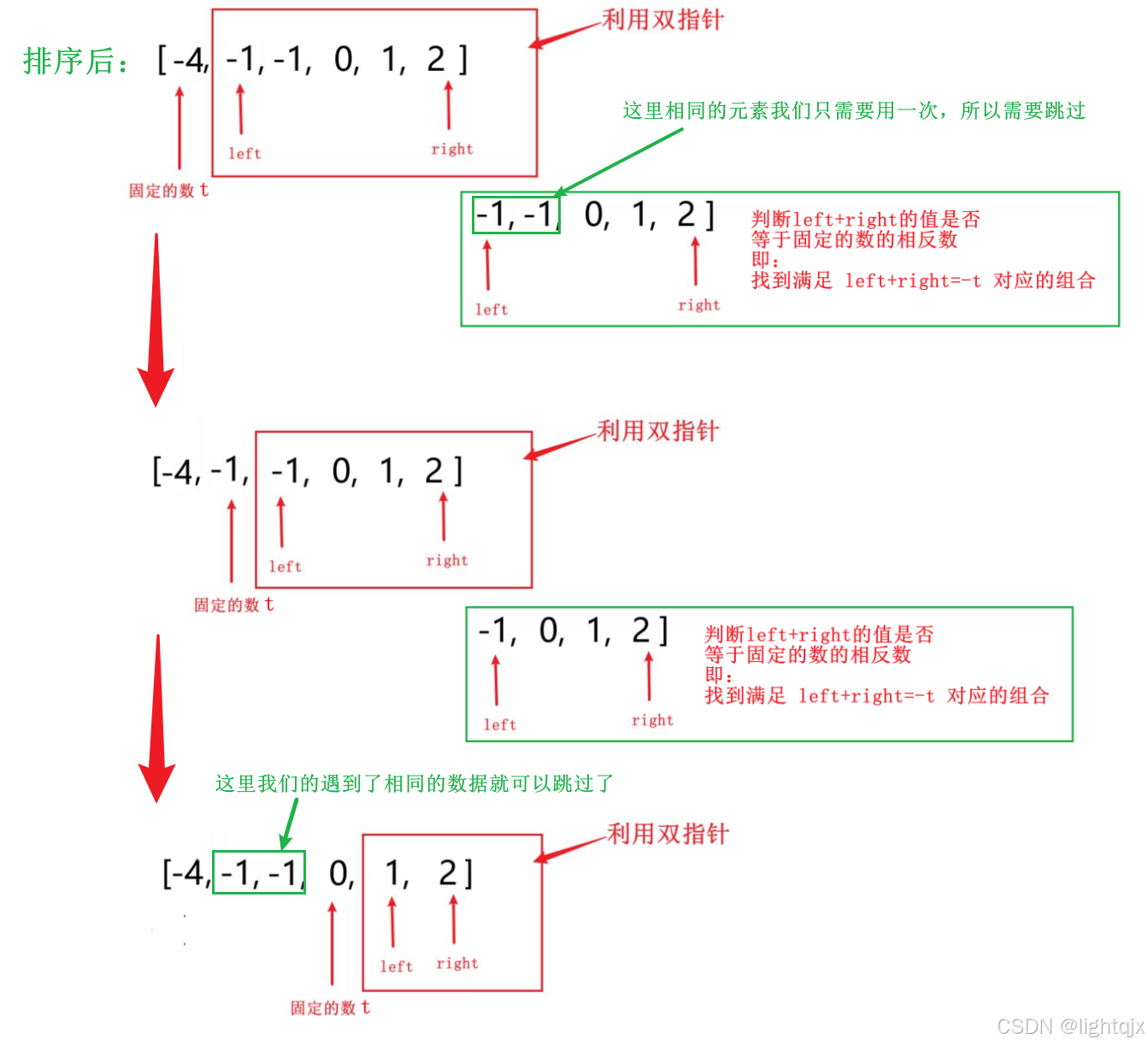

2. 代码实现

C++代码实现如下：

cpp 复制代码

class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
        sort(nums.begin(), nums.end());
        vector<vector<int>> vv;
        int n = nums.size();
        for (int i = 0; i < n - 2;)
        {
            if (nums[i] > 0) break;//优化
            int left = i + 1, right = n - 1;
            while (left < right)
            {
                int t = -nums[i];
                int sum = nums[left] + nums[right];
                if (sum > t)
                {
                    right--; while (left < right && nums[right] == nums[right + 1]) right--;
                }
                else if (sum < t)
                {
                    left++; while (left < right && nums[left] == nums[left - 1]) left++;
                }
                else
                {
                    vv.push_back({ nums[i],nums[left],nums[right] });
                    left++;
                    right--;
                    while (left < right && nums[left] == nums[left - 1]) left++;
                    while (left < right && nums[right] == nums[right + 1]) right--;
                }
            }
            i++;
            while (i < left && nums[i] == nums[i - 1]) i++;
        }
        return vv;
    }
};

八、四数之和

题目链接：18. 四数之和 - 力扣（LeetCode）

1. 分析解决

这道题的解决方法是在三数之和的方法上实现的。所以我们还是先固定一个数a，在使用三数之和的方法在后续区间中去先固定b，再利用双指针遍历再后面的区间。即：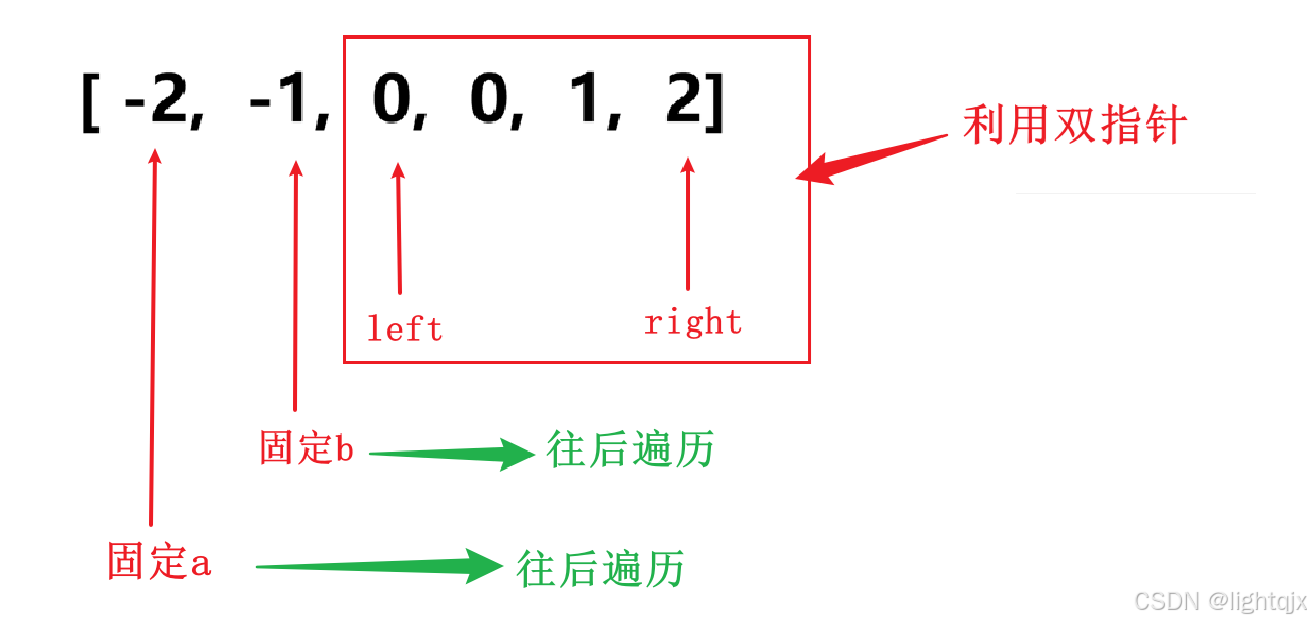

2. 代码实现

C++代码实现：

cpp 复制代码

class Solution {
public:
    vector<vector<int>> fourSum(vector<int>& nums, int target) 
    {
        //1.排序
        sort(nums.begin(), nums.end());
        //2.双指针
        vector<vector<int>> ret;
        for (int a = 0; a < nums.size();)//固定第一个数
        {
            for (int b = a + 1; b < nums.size();)//固定第二个数
            {
                //双指针
                int left = b + 1, right = nums.size() - 1;
                long long t = (long long)target - nums[a] - nums[b]; //在[left,right]中去找 t
                while (left < right)
                {
                    long long sum = nums[left] + nums[right];
                    if (sum > t) right--;
                    else if (sum < t) left++;
                    else
                    {
                        ret.push_back({ nums[a],nums[b],nums[left],nums[right] });
                        left++;
                        right--;
                        while (left < right && nums[left] == nums[left - 1]) left++;
                        while (left < right && nums[right] == nums[right + 1]) right--;
                    }
                }
                b++;
                while (b < nums.size() && nums[b] == nums[b - 1]) b++;
            }
            a++;
            while (a < nums.size() && nums[a] == nums[a - 1]) a++;
        }
        return ret;
    }
};

感谢各位观看！希望能多多支持！