【数据结构】建堆操作：向上调整与向下调整的数学推导与性能对比

🏠 个人主页: EXtreme35

📚 个人专栏:

专栏名称	专栏主题简述
《C语言》	C语言基础、语法解析与实战应用
《数据结构》	线性表、树、图等核心数据结构详解
《题解思维》	算法思路、解题技巧与高效编程实践

- 引言
- [I. 堆操作的时间复杂度分析](#I. 堆操作的时间复杂度分析)
- - [1. 堆的基本性质与高度](#1. 堆的基本性质与高度)
  - [1. 向上调整（AdjustUp）的建堆时间复杂度： O ( N log ⁡ N ) O(N \log N) O(NlogN)](#1. 向上调整（AdjustUp）的建堆时间复杂度： O ( N log ⁡ N ) O(N \log N) O(NlogN))
  - [2. 向下调整（AdjustDown）的建堆时间复杂度： O ( N ) O(N) O(N)](#2. 向下调整（AdjustDown）的建堆时间复杂度： O ( N ) O(N) O(N))
- [II. Top-K 问题](#II. Top-K 问题)
- - [1. 核心策略](#1. 核心策略)
  - [2.Top-K 问题的时间复杂度分析](#2.Top-K 问题的时间复杂度分析)
- [III. 总结](#III. 总结)

引言

堆（Heap）是一种特殊的完全二叉树 数据结构，通常用于实现优先队列 。堆的性质要求：在大顶堆中，任意节点的值都大于或等于其子节点的值；在小顶堆中，任意节点的值都小于或等于其子节点的值。堆排序（Heap Sort）是基于堆这种数据结构的一种高效排序算法，其核心操作在于元素的向上调整（AdjustUp）和向下调整（AdjustDown），这两种操作对于维护堆的性质至关重要。

本文将首先深入探究堆排序中向上调整和向下调整操作的时间复杂度 ，通过详细的数学分析证明其效率。随后，我们将利用堆的特性，结合您提供的 C 语言代码，详细阐述和实现一个经典的算法问题------Top-K 问题，即从一个大规模数据集中找出最大的 K 个元素。

I. 堆操作的时间复杂度分析

在堆中，向上调整和向下调整操作是维持堆性质的基础，尤其在插入元素（向上调整）和删除堆顶元素（向下调整）时。

1. 堆的基本性质与高度

一个包含 N N N 个元素的完全二叉树（即堆）的高度 H H H 是 O ( log ⁡ N ) O(\log N) O(logN)。
H = ⌊ log ⁡ 2 N ⌋ H = \lfloor \log_2 N \rfloor H=⌊log2N⌋

证明：假设一个满二叉树有 N N N 个节点，其高度为 H H H (根节点所在的层记为第 1 层，则叶子节点在第 H − 1 H-1 H−1 层)。则节点总数 N N N 满足：
N = 1 + 2 + 4 + ⋯ + 2 H-1 = 2 H − 1 N = 1 + 2 + 4 + \dots + 2^\text{H-1} = 2^{H} - 1 N=1+2+4+⋯+2H-1=2H−1

解出 H H H : N + 1 = 2 H + 1 N+1 = 2^{H+1} N+1=2H+1 → \rightarrow → log ⁡ 2 ( N + 1 ) = H + 1 \log_2(N+1) = H+1 log2(N+1)=H+1 → \rightarrow → H = log ⁡ 2 ( N + 1 ) H = \log_2(N+1) H=log2(N+1)

对于一个具有 N N N 个节点的完全二叉树，其节点数 N N N 满足：

2 H ≤ N ≤ 2 H + 1 − 1 2^H \le N \le 2^{H+1} - 1 2H≤N≤2H+1−1

其中 H H H 是其高度（最高层的索引）。

从左侧不等式 2 H ≤ N 2^H \le N 2H≤N 可得： H ≤ log ⁡ 2 N H \le \log_2 N H≤log2N

从右侧不等式 N ≤ 2 H + 1 − 1 N \le 2^{H+1} - 1 N≤2H+1−1 可得：

N + 1 ≤ 2 H + 1 → log ⁡ 2 ( N + 1 ) ≤ H + 1 → H ≥ log ⁡ 2 ( N + 1 ) − 1 N+1 \le 2^{H+1} \rightarrow \log_2(N+1) \le H+1 \rightarrow H \ge \log_2(N+1) - 1 N+1≤2H+1→log2(N+1)≤H+1→H≥log2(N+1)−1

综合这两个不等式，完全二叉树的高度 H H H 满足：
log ⁡ 2 ( N + 1 ) − 1 ≤ H ≤ log ⁡ 2 N \log_2(N+1) - 1 \le H \le \log_2 N log2(N+1)−1≤H≤log2N

因此，对于足够大的 N N N，堆的高度 H H H 渐进地趋近于 log ⁡ 2 N \log_2 N log2N，记为 O ( log ⁡ N ) O(\log N) O(logN)。

1. 向上调整（AdjustUp）的建堆时间复杂度： O ( N log ⁡ N ) O(N \log N) O(NlogN)

向上调整操作用于在堆尾插入一个新元素后，恢复堆的性质。新元素位于子节点位置，通过与其父节点比较，如果新元素不满足堆的性质（例如，在小顶堆中，子节点小于父节点），则交换它们的位置，并继续向上比较，直到根节点或满足堆性质为止。

操作过程分析：

比较与交换： 循环内，比较 a[child] 和 a[parent]，若 a[child] < a[parent]，则执行一次交换操作。
移动： 交换后，child 变为原来的 parent，parent 重新计算为新的 (child - 1) / 2。

在每一次循环中，元素至多向上移动一层，即：

操作次数 ≤ 1 \text{操作次数} \le 1 操作次数≤1

移动距离 = 1 层 \text{移动距离} = 1 \text{ 层} 移动距离=1 层

该过程从叶子节点（最深层 H H H）开始，一直向上追溯到根节点。最坏情况是元素从最底层一直移动到根节点，路径长度恰好等于堆的高度 H H H。

推导过程： 为简化计算，我们以 h h h 层满二叉树为例进行分析，若规定根结点层数为 1。

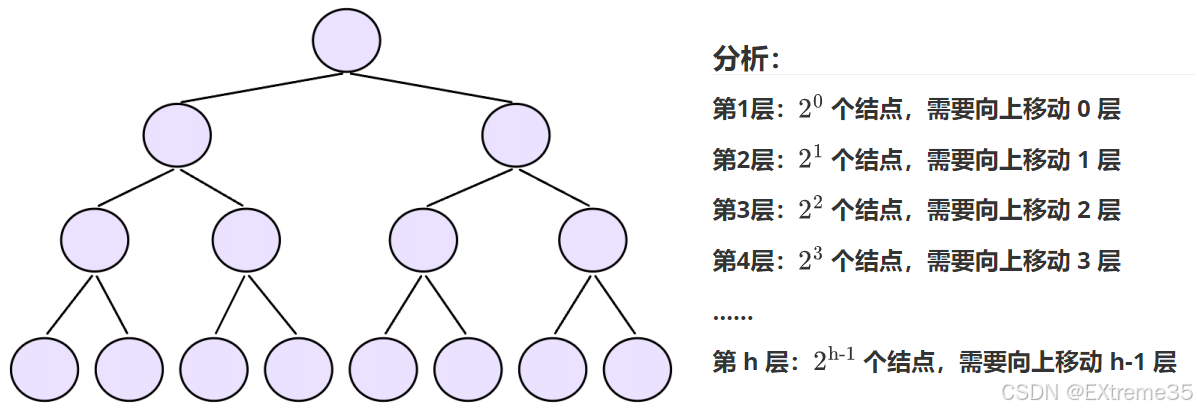
则第 i i i 层的结点数 n i = 2 i − 1 n_i = 2^{i-1} ni=2i−1，该层结点向上调整的最大移动层数为 i − 1 i-1 i−1，总移动步数 T ( h ) T(h) T(h) 是：每层结点个数 * 向上调整次数（第⼀层调整次数为0）

T ( h ) = ∑ i = 1 h 2 i − 1 ⋅ ( i − 1 ) T(h) = \sum_{i=1}^{h} 2^{i-1} \cdot (i-1) T(h)=i=1∑h2i−1⋅(i−1)

展开求和项，并令 j = i − 1 j = i-1 j=i−1:

T ( h ) = ∑ j = 0 h − 1 2 j ⋅ j = 2 1 ⋅ 1 + 2 2 ⋅ 2 + 2 3 ⋅ 3 + ⋯ + 2 h − 1 ⋅ ( h − 1 ) ( 1 ) T(h) = \sum_{j=0}^{h-1} 2^j \cdot j = 2^1 \cdot 1 + 2^2 \cdot 2 + 2^3 \cdot 3 + \dots + 2^{h-1} \cdot (h-1) \quad (\text{1}) T(h)=j=0∑h−12j⋅j=21⋅1+22⋅2+23⋅3+⋯+2h−1⋅(h−1)(1)

使用错位相减法。将 (1) \text{(1)} (1) 式乘以公比 r = 2 r=2 r=2:

2 ⋅ T ( h ) = 2 2 ⋅ 1 + 2 3 ⋅ 2 + 2 4 ⋅ 3 + ⋯ + 2 h − 1 ⋅ ( h − 2 ) + 2 h ⋅ ( h − 1 ) ( 2 ) 2 \cdot T(h) = 2^2 \cdot 1 + 2^3 \cdot 2 + 2^4 \cdot 3 + \dots + 2^{h-1} \cdot (h-2) + 2^h \cdot (h-1) \quad (\text{2} ) 2⋅T(h)=22⋅1+23⋅2+24⋅3+⋯+2h−1⋅(h−2)+2h⋅(h−1)(2)

用 (2) \text{(2)} (2) 式减去 (1) \text{(1)} (1) 式： T ( h ) = 2 ⋅ T ( h ) − T ( h ) T(h) = 2 \cdot T(h) - T(h) T(h)=2⋅T(h)−T(h)

T ( h ) = − 2 1 ⋅ 1 + ( 2 2 ⋅ 1 ) + ( 2 3 ⋅ 1 ) + ⋯ + ( 2 h − 1 ⋅ 1 ) + 2 h ⋅ ( h − 1 ) T(h) = -2^1 \cdot 1 + (2^2 \cdot 1) + (2^3 \cdot 1) + \dots + (2^{h-1} \cdot 1) + 2^h \cdot (h-1) T(h)=−21⋅1+(22⋅1)+(23⋅1)+⋯+(2h−1⋅1)+2h⋅(h−1)

为了凑成完整的等比数列求和 ∑ i = 0 h − 1 2 i = 2 h − 1 \sum_{i=0}^{h-1} 2^i = 2^h - 1 ∑i=0h−12i=2h−1，我们将 2 0 = 1 2^0=1 20=1 加到等式两边：

T ( h ) = − ( 2 0 + 2 1 + 2 2 + ⋯ + 2 h − 1 ) + 2 h ⋅ ( h − 1 ) + 2 0 T(h) = -(2^0 + 2^1 + 2^2 + \dots + 2^{h-1}) + 2^h \cdot (h-1) + 2^0 T(h)=−(20+21+22+⋯+2h−1)+2h⋅(h−1)+20

T ( h ) = − ∑ i = 0 h − 1 2 i + 2 h ⋅ ( h − 1 ) + 1 T(h) = -\sum_{i=0}^{h-1} 2^i + 2^h \cdot (h-1) + 1 T(h)=−∑i=0h−12i+2h⋅(h−1)+1

T ( h ) = − ( 2 h − 1 ) + 2 h ⋅ ( h − 1 ) + 1 T(h) = -(2^h - 1) + 2^h \cdot (h-1) + 1 T(h)=−(2h−1)+2h⋅(h−1)+1

T ( h ) = − 2 h + 1 + h ⋅ 2 h − 2 h + 1 T(h) = -2^h + 1 + h \cdot 2^h - 2^h + 1 T(h)=−2h+1+h⋅2h−2h+1

T ( h ) = h ⋅ 2 h − 2 ⋅ 2 h + 2 T(h) = h \cdot 2^h - 2 \cdot 2^h + 2 T(h)=h⋅2h−2⋅2h+2

T ( h ) = 2 h ( h − 2 ) + 2 T(h) = 2^h (h - 2) + 2 T(h)=2h(h−2)+2

将结点总数 N = 2 h − 1 N = 2^h - 1 N=2h−1 和高度 h = log ⁡ 2 ( N + 1 ) h = \log_2(N+1) h=log2(N+1) 代入得：
F ( N ) = ( N + 1 ) ( log ⁡ 2 ( N + 1 ) − 2 ) + 2 F(N) = (N+1)(\log_2(N+1) - 2) + 2 F(N)=(N+1)(log2(N+1)−2)+2

因此，向上调整算法的建堆时间复杂度为：
T A d j u s t U p _ B u i l d = O ( N log ⁡ N ) T_{AdjustUp\_Build} = O(N \log N) TAdjustUp_Build=O(NlogN)

2. 向下调整（AdjustDown）的建堆时间复杂度： O ( N ) O(N) O(N)

向下调整 操作通常用于删除堆顶元素（用堆尾元素替换堆顶后）或在建堆过程中，用于将一个不符合堆性质的子树调整为堆。操作从父节点开始，与其左右孩子节点中满足条件的那个孩子进行比较，如果不满足堆性质，则交换，并向下递归，直到满足堆性质或到达叶子节点。

操作过程分析：

确定孩子： 确定左右孩子中较小的那个孩子 child。
比较与交换： 比较 a[child] 和 a[parent]。若 a[child] < a[parent]，则执行一次交换操作。
移动： 交换后，parent 变为原来的 child，child 重新计算为新的 parent * 2 + 1。

在每一次循环中，元素至多向下移动一层，即：

操作次数 ≤ 1 \text{操作次数} \le 1 操作次数≤1
移动距离 = 1 层 \text{移动距离} = 1 \text{ 层} 移动距离=1 层

该过程从根节点（第 1 层）开始，一直向下追溯到叶子节点（最深层 H H H）。最坏情况是元素从根节点一直向下移动到最底层，路径长度恰好等于堆的高度 H H H。

该方法从最后一个非叶子结点开始，依次对所有非叶子结点执行一次向下调整操作。

推导过程： 同样以 h h h 层满二叉树为例。若规定根结点层数为 1，则第 i i i 层的结点数 n i = 2 i − 1 n_i = 2^{i-1} ni=2i−1，该层结点向下调整的最大移动层数为 h − i h-i h−i。

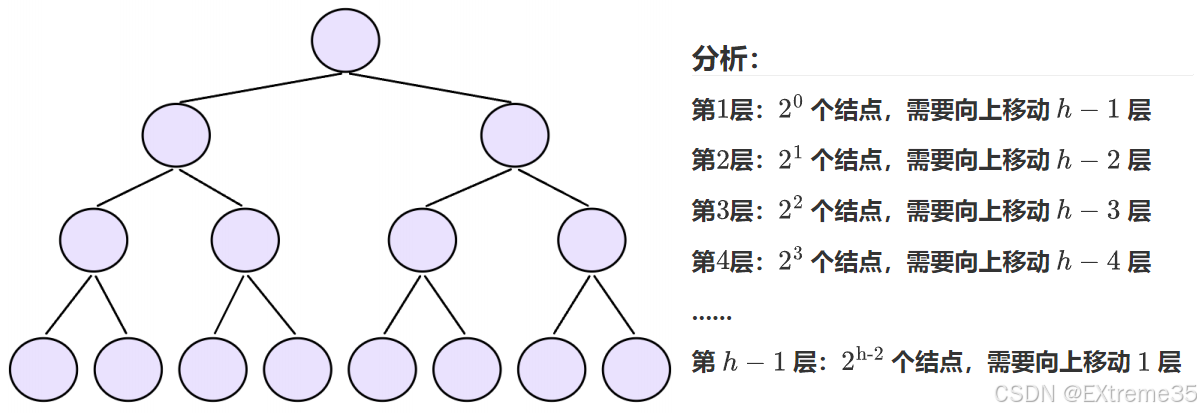
总移动步数 T ( h ) T(h) T(h) 是每层结点数与其最大向下调整次数的乘积之和：
T ( h ) = ∑ i = 1 h − 1 2 i − 1 ⋅ ( h − i ) T(h) = \sum_{i=1}^{h-1} 2^{i-1} \cdot (h-i) T(h)=i=1∑h−12i−1⋅(h−i)

展开求和项，并令 j = i − 1 j = i-1 j=i−1:
T ( h ) = ∑ j = 1 h − 1 2 j ⋅ ( h − 1 − j ) = 2 0 ⋅ ( h − 1 ) + 2 1 ⋅ ( h − 2 ) + 2 2 ⋅ ( h − 3 ) + 2 3 ⋅ ( h − 4 ) + ⋯ + 2 h − 3 ⋅ 2 + 2 h − 2 ⋅ 1 ( 1 ) T(h) = \sum_{j=1}^{h-1} 2^j \cdot (h-1-j) = 2^0\cdot(h-1) + 2^1\cdot(h-2) + 2^2\cdot(h-3) +2^3\cdot(h-4)+ \dots + 2^{h-3}\cdot2+2^{h-2}\cdot1 \quad (\text{1}) T(h)=j=1∑h−12j⋅(h−1−j)=20⋅(h−1)+21⋅(h−2)+22⋅(h−3)+23⋅(h−4)+⋯+2h−3⋅2+2h−2⋅1(1)

使用错位相减法。将 (1) \text{(1)} (1) 式乘以公比 r = 2 r=2 r=2：
2 ⋅ T ( h ) = 2 1 ⋅ ( h − 1 ) + 2 2 ⋅ ( h − 2 ) + 2 3 ⋅ ( h − 3 ) + 2 4 ⋅ ( h − 4 ) + ⋯ + 2 h − 2 ⋅ 2 + 2 h − 1 ⋅ 1 ( 2 ) 2 \cdot T(h) = 2^1\cdot(h-1) + 2^2\cdot(h-2) + 2^3\cdot(h-3) +2^4\cdot(h-4)+ \dots + 2^{h-2}\cdot2+2^{h-1}\cdot1 \quad (\text{2}) 2⋅T(h)=21⋅(h−1)+22⋅(h−2)+23⋅(h−3)+24⋅(h−4)+⋯+2h−2⋅2+2h−1⋅1(2)

用 (2) \text{(2)} (2) 式减去 (1) \text{(1)} (1) 式： T ( h ) = 2 ⋅ T ( h ) − T ( h ) T(h) = 2 \cdot T(h) - T(h) T(h)=2⋅T(h)−T(h)
T ( h ) = − 2 0 ( h − 1 ) + 2 1 + 2 2 + 2 3 + 2 4 + ⋯ + 2 h − 2 + 2 h − 1 T(h) = -2^0(h-1) + 2^1 + 2^2 + 2^3 + 2^4+ \dots +2^{h-2}+ 2^{h-1} T(h)=−20(h−1)+21+22+23+24+⋯+2h−2+2h−1

为了凑成完整的等比数列 ∑ i = 0 h − 1 2 i = 2 h − 1 \sum_{i=0}^{h-1} 2^i = 2^h - 1 ∑i=0h−12i=2h−1，我们将 2 0 = 1 2^0=1 20=1 加到第一部分，并进行整理：

T ( h ) = 2 0 + 2 1 + 2 2 + ⋯ + 2 h − 1 − h T(h) = 2^0 + 2^1 + 2^2 + \dots + 2^{h-1} - h T(h)=20+21+22+⋯+2h−1−h

T ( h ) = ∑ i = 0 h − 1 2 i − h T(h) = \sum_{i=0}^{h-1} 2^i - h T(h)=∑i=0h−12i−h

T ( h ) = ( 2 h − 1 ) − h T(h) = (2^h - 1) - h T(h)=(2h−1)−h

将结点总数 N = 2 h − 1 N = 2^h - 1 N=2h−1 和高度 h = log ⁡ 2 ( N + 1 ) h = \log_2(N+1) h=log2(N+1) 代入：
T ( N ) = N − log ⁡ 2 ( N + 1 ) T(N) = N - \log_2(N+1) T(N)=N−log2(N+1)

由于 N N N 远大于 log ⁡ 2 ( N + 1 ) \log_2(N+1) log2(N+1)，因此该建堆方法的时间复杂度为：
T A d j u s t D o w n _ B u i l d = O ( N ) T_{AdjustDown\_Build} = O(N) TAdjustDown_Build=O(N)

II. Top-K 问题

TOP-K问题： 即从 N N N 个数据中找出前 K K K个最⼤的元素或者最⼩的元素，⼀般情况下数据量都⽐较⼤。

⽐如：专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。

对于Top-K问题，能想到的最简单直接的⽅式就是排序，但是：如果数据量⾮常⼤，排序就不太可取了(可能数据都不能⼀下⼦全部加载到内存中)。最佳的⽅式就是⽤堆来解决，基本思路如下：

⽤数据集合中前K个元素来建堆
- 前 K K K个最⼤的元素，则建小堆。
- 前 K K K个最⼩的元素，则建大堆。
⽤剩余的 N − K N-K N−K个元素依次与堆顶元素 来⽐较，不满⾜则替换堆顶元素。

将剩余 N − K N-K N−K个元素依次与堆顶元素⽐完之后，堆中剩余的 K K K个元素就是所求的前 K K K个最小或者最大的元素。

1. 核心策略

为了高效地找出前 K K K 个最大的元素，我们维护一个大小为 K K K 的小顶堆 （Min-Heap）。

为什么选择小顶堆？

小顶堆的堆顶元素是这 K K K 个数中的最小值。
我们想要找到的是最大的 K K K 个数。当遍历到一个新的数 X X X 时，如果 X X X 比堆顶的最小值还要大，说明 X X X 有资格成为前 K K K 大的数之一。此时，我们用 X X X 替换掉堆顶的最小值，然后对堆进行向下调整，确保堆中仍然是当前遍历到的所有数中的最大 K K K 个数。

具体步骤：

阶段一： 读取数据流中的前 K K K 个数，并用这 K K K 个数建立一个大小为 K K K 的小顶堆 ，使用向下调整算法，时间复杂度为 O ( N ) O(N) O(N)。

c 复制代码

  // 阶段一：读取文件中前k个数并建堆
  for (int i = 0; i < k; i++)
  {
      fscanf(fout, "%d", &kminheap[i]);
  }
  // 建立K个数的小顶堆
  // 从最后一个非叶子节点开始向下调整
  for (int i = (k - 1 - 1) / 2; i >= 0; i--) 
  {
      AdjustDown(kminheap, k, i);
  }

阶段二：遍历与调整
- 从第 K + 1 K+1 K+1 个数开始，依次读取剩下的 N − K N-K N−K 个数 X X X。
- 判断： 如果 X > 堆顶元素 X > \text{堆顶元素} X>堆顶元素（即 X X X 大于当前已知的 K K K 个最大数中的最小值），则执行替换。
- 替换与调整： 将堆顶元素替换为 X X X，然后对新的堆顶执行向下调整（AdjustDown） 操作，以恢复小顶堆的性质。
- 向下调整的时间复杂度： O ( log ⁡ K ) O(\log K) O(logK)。

c 复制代码

// 阶段二：读取剩下的N-K个数并调整堆
int x = 0;
while (fscanf(fout, "%d", &x) > 0)
{
    // 核心判断：如果新读取的数比堆顶（K个数中的最小值）大
    if (x > kminheap[0]) 
    {
        // 替换堆顶
        kminheap[0] = x;
        // 向下调整，恢复小顶堆性质
        AdjustDown(kminheap, k, 0); 
    }
}

阶段三： 遍历结束后，堆中剩下的 K K K 个元素即为原数据流中最大的 K K K 个数。

c 复制代码

// 阶段三：输出结果
printf("最大前%d个数：", k);
for (int i = 0; i < k; i++)
{
    printf("%d ", kminheap[i]);
}
printf("\n");

2.Top-K 问题的时间复杂度分析

假设数据流中的总数据量为 N N N，我们需要找出最大的 K K K 个数。

阶段一：建堆
- 读取前 K K K 个数： O ( K ) O(K) O(K)
- 建立大小为 K K K 的小顶堆（通过 O ( K ) O(K) O(K) 次 AdjustDown 操作）： O ( K ) O(K) O(K)
- 总时间： T I n i t = O ( K ) T_{Init} = O(K) TInit=O(K)
阶段二：遍历与调整
- 需要处理 N − K N-K N−K 个数。
- 对于每个数 X X X，判断是否大于堆顶 O ( 1 ) O(1) O(1)。
- 如果需要替换，则执行一次向下调整 AdjustDown 操作。
- AdjustDown 操作在大小为 K K K 的堆上，时间复杂度为 O ( log ⁡ K ) O(\log K) O(logK)。
- 总时间： T L o o p = ( N − K ) × O ( log ⁡ K ) = O ( ( N − K ) log ⁡ K ) T_{Loop} = (N-K) \times O(\log K) = O((N-K) \log K) TLoop=(N−K)×O(logK)=O((N−K)logK)
最终时间复杂度
- T T o t a l = T I n i t + T L o o p = O ( K ) + O ( ( N − K ) log ⁡ K ) T_{Total} = T_{Init} + T_{Loop} = O(K) + O((N-K) \log K) TTotal=TInit+TLoop=O(K)+O((N−K)logK)
- 由于 N N N 往往远大于 K K K，所以 N − K ≈ N N-K \approx N N−K≈N。
- T T o p K ≈ O ( N log ⁡ K ) T_{TopK} \approx O(N \log K) TTopK≈O(NlogK)

优势分析：

相比于直接对所有 N N N 个元素进行排序（时间复杂度 O ( N log ⁡ N ) O(N \log N) O(NlogN)），堆方法的时间复杂度 O ( N log ⁡ K ) O(N \log K) O(NlogK) 要高效得多，尤其当 K ≪ N K \ll N K≪N 时。例如，在一个包含十亿（ 1 0 9 10^9 109）个数据的集合中找前 100 个最大的数：

O ( N log ⁡ N ) ≈ 1 0 9 × log ⁡ 2 ( 1 0 9 ) ≈ 1 0 9 × 30 O(N \log N) \approx 10^9 \times \log_2(10^9) \approx 10^9 \times 30 O(NlogN)≈109×log2(109)≈109×30
O ( N log ⁡ K ) ≈ 1 0 9 × log ⁡ 2 ( 100 ) ≈ 1 0 9 × 6.6 O(N \log K) \approx 10^9 \times \log_2(100) \approx 10^9 \times 6.6 O(NlogK)≈109×log2(100)≈109×6.6

可见，使用堆解决 Top-K 问题的效率提升是巨大的，这使得该算法成为处理大数据集中 Top-K 问题的首选方法。

III. 总结

本文对堆排序的核心调整操作进行了严格的时间复杂度分析：

向上调整建堆（AdjustUp）： 最坏时间复杂度为 O ( N log ⁡ N ) O(N \log N) O(NlogN)。
向下调整建堆（AdjustDown）： 最坏时间复杂度为 O ( N ) O(N) O(N)。
建堆操作（Build Heap）： 通过 N N N 次 O ( log ⁡ N ) O(\log N) O(logN) 的向下调整 的求和分析，证明其总时间复杂度为线性的 O ( N ) O(N) O(N)。

在此基础上，我们利用堆的特性，实现了 Top-K 问题的最优解法。通过维护一个大小为 K K K 的小顶堆，算法避免了对全数据集的完全排序，将时间复杂度优化至 O ( N log ⁡ K ) O(N \log K) O(NlogK)，使其成为处理大规模数据集中 Top-K 问题的最有效策略之一。

【数据结构】建堆操作：向上调整与向下调整的数学推导与性能对比

目录

引言

I. 堆操作的时间复杂度分析

1. 堆的基本性质与高度

1. 向上调整（AdjustUp）的建堆时间复杂度： O ( N log ⁡ N ) O(N \log N) O(NlogN)

2. 向下调整（AdjustDown）的建堆时间复杂度： O ( N ) O(N) O(N)

II. Top-K 问题

1. 核心策略

2.Top-K 问题的时间复杂度分析

III. 总结