拉格朗日插值
一、Lagrange插值公式
1.1、线性插值
我们知道两点可以确定一条直线,当只有两个节点 x 0 、 x 1 x_0、x_1 x0、x1,用过两点 ( x 0 , y 0 ) 、 ( x 1 , y 1 ) (x_0,y_0)、(x_1, y_1) (x0,y0)、(x1,y1)的直线 y = L 1 ( x ) y=L_1(x) y=L1(x)近似代替曲线 y = f ( x ) y=f(x) y=f(x),即 f ( x ) ≈ L 1 ( x ) f(x) \approx L_1(x) f(x)≈L1(x). 由直线的点斜方程可得:
y − y 0 = y 1 − y 0 x 1 − x 0 ( x − x 0 ) y-y_0=\frac{y_1-y_0}{x_1-x_0}(x-x_0) y−y0=x1−x0y1−y0(x−x0)
移项得到:
y = y 1 x 1 − x 0 ( x − x 0 ) − y 0 x 1 − x 0 ( x − x 0 ) + y 0 y=\frac{y_1}{x_1-x_0}(x-x_0)-\frac{y_0}{x_1-x_0}(x-x_0)+y_0 y=x1−x0y1(x−x0)−x1−x0y0(x−x0)+y0
整理得到:
y = L 1 ( x ) = x − x 0 x 1 − x 0 y 1 + x 1 − x x 1 − x 0 y 0 = x − x 1 x 0 − x 1 y 0 + x − x 0 x 1 − x 0 y 1 y=L_1(x)=\frac{x-x_0}{x_1-x_0}y_1+\frac{x_1-x}{x_1-x_0}y_0 \\=\frac{x-x_1}{x_0-x_1}y_0+\frac{x-x_0}{x_1-x_0}y_1 y=L1(x)=x1−x0x−x0y1+x1−x0x1−xy0=x0−x1x−x1y0+x1−x0x−x0y1
上式满足插值条件: L 1 ( x 0 ) = y 0 , L 2 ( x 1 ) = y 1 L_1(x_0)=y_0,L_2(x_1)=y_1 L1(x0)=y0,L2(x1)=y1,并且插值函数 L 1 ( x ) L_1(x) L1(x)是线性函数,故称上式为线性插值公式。
插值公式是由两个一次多项式 l 0 ( x ) l_0(x) l0(x) 和 l 1 ( x ) l_1(x) l1(x) 组成的线性组合。
公式:
l 0 ( x ) = x − x 1 x 0 − x 1 l_0(x) = \frac{x-x_1}{x_0-x_1} l0(x)=x0−x1x−x1
l 1 ( x ) = x − x 0 x 1 − x 0 l_1(x) = \frac{x-x_0}{x_1-x_0} l1(x)=x1−x0x−x0
含义: 这两个函数是插值的"积木"(数学上称为基)。最终的插值多项式 L 1 ( x ) L_1(x) L1(x) 就是把这两个积木按照高度 y 0 y_0 y0 和 y 1 y_1 y1 堆起来: L 1 ( x ) = y 0 ⋅ l 0 ( x ) + y 1 ⋅ l 1 ( x ) L_1(x) = y_0 \cdot l_0(x) + y_1 \cdot l_1(x) L1(x)=y0⋅l0(x)+y1⋅l1(x)
基函数的核心性质:"归一性"和"零点性"
性质描述:
当 x = x 0 x = x_0 x=x0 时: l 0 ( x 0 ) = 1 l_0(x_0) = 1 l0(x0)=1,而 l 1 ( x 0 ) = 0 l_1(x_0) = 0 l1(x0)=0。
当 x = x 1 x = x_1 x=x1 时: l 1 ( x 1 ) = 1 l_1(x_1) = 1 l1(x1)=1,而 l 0 ( x 1 ) = 0 l_0(x_1) = 0 l0(x1)=0。
数学总结:用一个公式总结了这个性质:
l k ( x i ) = δ i k = { 1 , i = k 0 , i ≠ k l_k(x_i) = \delta_{ik} = \begin{cases} 1, & i=k \\ 0, & i \neq k \end{cases} lk(xi)=δik={1,0,i=ki=k
这被称为 克罗内克函数(Kronecker delta) 性质。
1.2、Lagrange插值基函数
对上面的线性插值进行推广,可以对 n + 1 n+1 n+1个节点构造 n n n次的拉格朗日多项式。
目标就是找出这样一个式子,找一个函数 L n ( x ) L_n(x) Ln(x),他是由 n + 1 n+1 n+1个基组合的:
L n ( x ) = ∑ k = 0 n y k l k ( x ) L_n(x)=\sum_{k=0}^ny_kl_k(x) Ln(x)=k=0∑nyklk(x)
这个函数必须经过所有给定数据点 ( x i , y i ) (x_i,y_i) (xi,yi)
这里面涉及到一个关键的基函数 l k ( x ) l_k(x) lk(x) 的构造
上面说过基函数需要满足两个性质:1. 零点性 2. 归一性
所以第一步先构造零点性:
为了让 l k ( x ) l_k(x) lk(x) 在除了 x k x_k xk 以外的其他所有节点( x 0 , ... , x k − 1 , x k + 1 , ... x_0, \dots, x_{k-1}, x_{k+1}, \dots x0,...,xk−1,xk+1,...)上都等于 0,分子必须包含这些点对应的因子: 分子 = ( x − x 0 ) ⋯ ( x − x k − 1 ) ( x − x k + 1 ) ⋯ ( x − x n ) \text{分子} = (x-x_0)\cdots(x-x_{k-1})(x-x_{k+1})\cdots(x-x_n) 分子=(x−x0)⋯(x−xk−1)(x−xk+1)⋯(x−xn)
第二步构造归一性:
为了让 l k ( x ) l_k(x) lk(x) 在 x = x k x = x_k x=xk 时恰好等于 1,我们需要除以一个常数。这个常数就是把 x x x 替换成 x k x_k xk 后的分子值:
分母 = ( x k − x 0 ) ⋯ ( x k − x k − 1 ) ( x k − x k + 1 ) ⋯ ( x k − x n ) \text{分母} = (x_k-x_0)\cdots(x_k-x_{k-1})(x_k-x_{k+1})\cdots(x_k-x_n) 分母=(xk−x0)⋯(xk−xk−1)(xk−xk+1)⋯(xk−xn)
于是最终公式为:
l k ( x ) = ∏ i = 0 i ≠ k n x − x i x k − x i l_k(x) = \prod_{\substack{i=0 \\ i \neq k}}^{n} \frac{x-x_i}{x_k-x_i} lk(x)=i=0i=k∏nxk−xix−xi
l k ( x ) l_k(x) lk(x) 被称为Lagrange基本插值多项式
1.3、Lagrange插值多项式
综合1.2中的内容可以推出最终公式
L n ( x ) = ∑ k = 0 n y k Π i = 0 , i ≠ k n x − x i x k − x i L_n(x)=\sum_{k=0}^ny_k\Pi_{i=0, i \neq k}^n \frac{x-x_i}{x_k-x_i} Ln(x)=k=0∑nykΠi=0,i=knxk−xix−xi
1.4、抛物线插值
线性插值是当 n = 1 n = 1 n=1 时的Lagange插值多项式是线性插值,那么当 n = 2 n=2 n=2 时的插值就是抛物线插值
当 n = 2 n=2 n=2 时,Lagrange插值为
L 2 ( x ) = ( x − x 1 ) ( x − x 2 ) ( x 0 − x 1 ) ( x 0 − x 2 ) y 0 + ( x − x 0 ) ( x − x 2 ) ( x 1 − x 0 ) ( x 1 − x 2 ) y 1 + ( x − x 0 ) ( x − x 1 ) ( x 2 − x 0 ) ( x 2 − x 1 ) y 2 L_2(x)=\frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)}y_0 + \frac{(x-x_0)(x-x_2)}{(x_1-x_0)(x_1-x_2)}y_1 + \frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)}y_2 L2(x)=(x0−x1)(x0−x2)(x−x1)(x−x2)y0+(x1−x0)(x1−x2)(x−x0)(x−x2)y1+(x2−x0)(x2−x1)(x−x0)(x−x1)y2
f ( x ) ≈ L 2 ( x ) f(x) \approx L_2(x) f(x)≈L2(x) 是用通过 ( x 0 , y 0 ) 、 ( x 1 , y 1 ) 、 ( x 2 , y 2 ) (x_0,y_0)、(x_1,y_1)、(x_2,y_2) (x0,y0)、(x1,y1)、(x2,y2) 三点的抛物线代替 y = f ( x ) y=f(x) y=f(x),所以 L 2 ( x ) L_2(x) L2(x) 也被称为抛物线插值公式
1.5、lagrange插值的形式
二、Lagrange插值的误差估计
2.1、Lagrange插值余项
余项就是估计函数与真实函数的误差,这个误差用余项表示:
定义余项(Remainder): R n ( x ) = f ( x ) − L n ( x ) R_n(x) = f(x) - L_n(x) Rn(x)=f(x)−Ln(x)
这表示真实值减去插值算出来的值。
2.2、Lagrange插值余项的表达式
R n ( x ) = f ( x ) − L n ( x ) = f ( n + 1 ) ( ξ ) ( n + 1 ) ! ω n + 1 ( x ) R_n(x) = f(x) - L_n(x) = \frac{f^{(n+1)}(\xi)}{(n+1)!} \omega_{n+1}(x) Rn(x)=f(x)−Ln(x)=(n+1)!f(n+1)(ξ)ωn+1(x)
其中:
R n ( x ) R_n(x) Rn(x):插值余项,即真实值 f ( x ) f(x) f(x) 与插值近似值 L n ( x ) L_n(x) Ln(x) 之间的差(误差)。
f ( n + 1 ) ( ξ ) f^{(n+1)}(\xi) f(n+1)(ξ):原函数 f ( x ) f(x) f(x) 的 n + 1 n+1 n+1 阶导数在某个特定点 ξ \xi ξ 的值。注意 ξ \xi ξ 是介于区间 ( a , b ) (a, b) (a,b) 内的一个未知点。
( n + 1 ) ! (n+1)! (n+1)!: n + 1 n+1 n+1 的阶乘。
ω n + 1 ( x ) \omega_{n+1}(x) ωn+1(x):这是一个多项式,等于 ( x − x 0 ) ( x − x 1 ) ⋯ ( x − x n ) (x-x_0)(x-x_1)\cdots(x-x_n) (x−x0)(x−x1)⋯(x−xn),即插值点与 x x x 距离的乘积。
这个公式告诉我们,插值的误差取决于两件事:
函数的平滑程度(由高阶导数 f ( n + 1 ) f^{(n+1)} f(n+1) 决定)。如果函数变化剧烈(高阶导数大),误差就大。
插值点的分布(由 ω n + 1 ( x ) \omega_{n+1}(x) ωn+1(x) 决定)。如果 x x x 离插值节点很远,误差也会变大。
虽然上面的误差公式很精确,但在实际计算中没法直接用,因为我们不知道那个 ξ \xi ξ 到底在哪里。
推论:
∣ R n ( x ) ∣ ⩽ M ( n + 1 ) ! ∣ ω n + 1 ( x ) ∣ |R_n(x)| \leqslant \frac{M}{(n+1)!} |\omega_{n+1}(x)| ∣Rn(x)∣⩽(n+1)!M∣ωn+1(x)∣
M M M:是 f ( n + 1 ) ( x ) f^{(n+1)}(x) f(n+1)(x) 在区间上的最大绝对值(上界)。
虽然我们要么算不出精确误差,但我们可以算出一个误差上限。也就是说,我们可以保证误差绝对不会超过这个数。
2.3、插值节点的选取
由于 R n ( x ) R_n(x) Rn(x) 正比于 ω n + 1 ( x ) \omega_{n+1}(x) ωn+1(x),所以当插值点多于 n + 1 n + 1 n+1 个的时候,尽量选择距离插值点 x x x 最近的那 n + 1 n + 1 n+1 个点。
三、例题
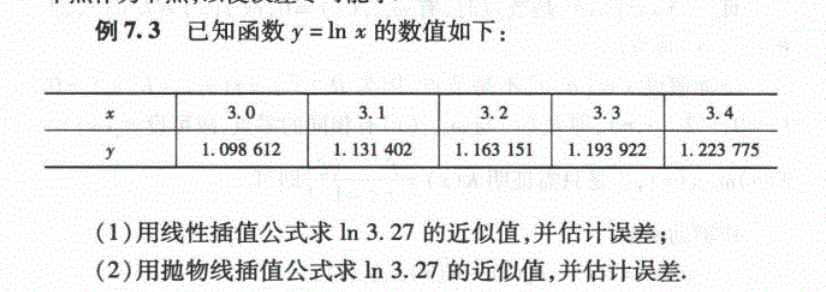
已知函数: y = ln x y = \ln x y=lnx(自然对数)。
已知数据表:给出了 x x x 从 3.0 到 3.4 的五个点,以及对应的精确函数值 y y y(保留了6位小数)。
例如:当 x = 3.2 x=3.2 x=3.2 时, y = 1.163151 y=1.163151 y=1.163151。
目标:计算 x = 3.27 x = 3.27 x=3.27 时的函数值 ln 3.27 \ln 3.27 ln3.27。
注意:3.27 并不在表格中,但它介于 3.2 和 3.3 之间。


