游游的you
题目信息:笔试真题
解法:贪心
题目地址:游游的you
题目描述
游游现在有a个'y',b个'o',c个'u',他想用这些字母拼成一个字符串。
三个相邻的字母是"you"可以获得2分,两个相邻的字母是"oo",可以获得1分。
问最多可以获得多少分?
输入描述
第一行一个整数q,代表询问次数。
接下来q行,每行三个正整数a,b,c,用空格隔开。
1≤ q ≤
1≤ a,b,c ≤输出描述
输出q行,代表每次询问的答案。
输入示例
题目解析
进行q次,每次取三个正整数a、b、c,分别代表y、o、u的数量,我们要做的是在有限的字母个数中,把分数拼凑到最高。
所以我们需要用到贪心的思维,先拼凑得分最高的 'you' 再考虑得分少的 'oo',然后把多余的遗弃掉或丢到最后面:
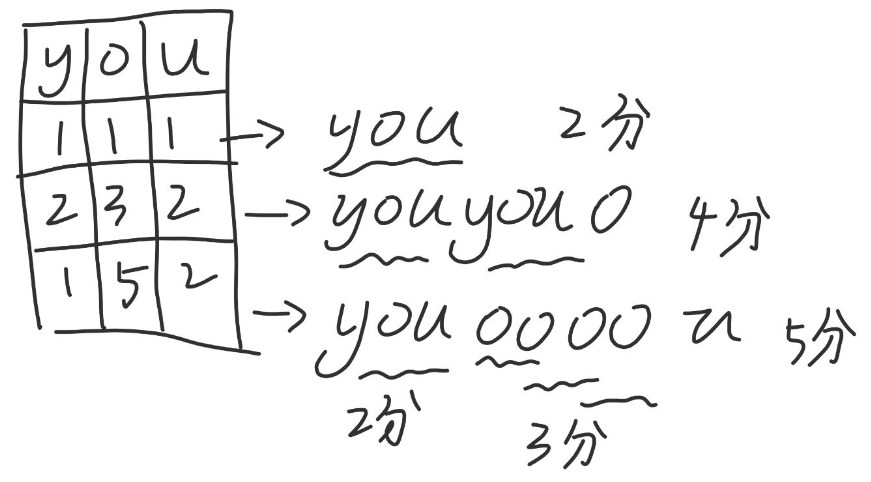
决定能拼凑多少个'you'取决于a、b、c的最小值,所以取min(a,b,c),而我们再计算剩余的'o'个数即可解决问题。
代码展示
#include <iostream>
using namespace std;
int q;
int a,b,c;
int main() {
cin >> q;
while(q--)
{
cin >> a >> b >> c;
int x = min(a,min(b,c));
int y = max(b-x-1,0);
cout << x*2 + y << endl;
}
}
// 64 位输出请用 printf("%lld")腐烂的苹果
解法:多源BFS(广度优先)+ 最短路径
题目地址:腐烂的苹果
描述
给定一个 n×m 的网格,其中每个单元格中可能有三种值中的一个 0 , 1 , 2。
其中 0 表示这个格子为空、1 表示这个格子有一个完好的苹果,2 表示这个格子有一个腐烂的苹果。
腐烂的苹果每分钟会向上下左右四个方向的苹果传播一次病菌,并导致相邻的苹果腐烂。请问经过多少分钟,网格中不存在完好的苹果。如果有苹果永远不会腐烂则返回 -1。
数据范围: 1≤n,m≤1000 ,网格中的值满足 0≤val≤2。
题目解析
由于可能有多个传染源,并且同时向四周扩散,所以我们要扩散完一轮后才能进行下一次扩散,所以我们就可以使用广度优先算法思路进行解题。
代码展示
class Solution {
public:
int n,m;
int dx[4] = {0,0,1,-1};
int dy[4] = {1,-1,0,0};
int rotApple(vector<vector<int> >& grid) {
n = grid.size();
m = grid[0].size();
bool vis[1005][1005] = {0};
queue<pair<int,int>> q;
int fresh = 0;
for(int i=0;i<n;i++)
{
for(int j=0;j<m;j++)
{
if(grid[i][j] == 2)
{
q.push({i,j});
vis[i][j] = true;
}
else if(grid[i][j] == 1) {
fresh++;
}
}
}
if(fresh == 0) return 0;
int ret = 0;
while(q.size())
{
int sz = q.size();
bool rotten = false;
while(sz--)
{
auto [a,b] = q.front();
q.pop();
for(int i=0;i<4;i++)
{
int x = a + dx[i];
int y = b + dy[i];
if(x>=0 && x<n && y>=0 && y<m && !vis[x][y] && grid[x][y] == 1)
{
vis[x][y] = true;
q.push({x,y});
fresh--;
rotten = true;
}
}
}
if(rotten) ret++;
}
bool cheek = false;
for(int i=0;i<n;i++)
{
for(int j=0;j<m;j++)
{
if(grid[i][j] == 1 && !vis[i][j]) {
cheek = true;
break;
}
}
if(cheek) break;
}
return cheek ? -1 : ret;
}
};孩子们的游戏
题目地址:孩子们的游戏
描述
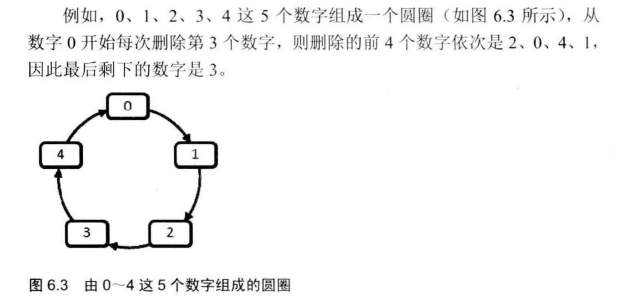
每年六一儿童节,牛客都会准备一些小礼物和小游戏去看望孤儿院的孩子们。其中,有个游戏是这样的:首先,让 n 个小朋友们围成一个大圈,小朋友们的编号是0~n-1。然后,随机指定一个数 m ,让编号为0的小朋友开始报数。每次喊到 m-1 的那个小朋友要出列唱首歌,然后可以在礼品箱中任意的挑选礼物,并且不再回到圈中,从他的下一个小朋友开始,继续0... m-1报数....这样下去....直到剩下最后一个小朋友,可以不用表演,并且拿到牛客礼品,请你试着想下,哪个小朋友会得到这份礼品呢?
数据范围:1≤n≤5000,1≤m≤10000
要求:空间复杂度 O(1),时间复杂度 O(n)
题目解析
本题为经典约瑟夫环问题:n 个小朋友编号 0~n-1 围成圈,从 0 号开始报数,每次报到 m-1 的小朋友出列,剩余小朋友从出列者下一位重新报数,直到只剩最后 1 个小朋友。
当 i 个小朋友时,第一个出列的编号是 (m-1) % i。
出列后剩余 i-1 个小朋友,从出列者的下一位(编号 m % i)重新报数,相当于将 i-1 个小朋友的编号 "偏移" 了 m 位。因此 i-1 个小朋友的编号 f (i-1),转换为 i 个小朋友的编号需加 m 后取模 i。
代码展示
class Solution {
public:
int LastRemaining_Solution(int n, int m) {
int f=0;
for(int i=2;i<=n;i++)f=(f+m)%i;
return f;
}
};今天的学习到此结束\\\\٩( 'ω' )و ////