在上一篇博客中我们建立的逻辑回归模型解决了银行贷款的二分类问题,但是不知道大家有没有注意到我们当时的召回率是非常低的,只有百分五十左右,这一次,我们就来学习如何进行逻辑回归的调优。
1、参数调整
原理
在逻辑回归的参数调整中,核心调优目标其实是正则化因子C------其他参数多为模型结构的选择项,而C的取值直接决定模型性能。那么正则化因子到底是什么?我们又该如何精准调整?你且听我娓娓道来。
我们之前提到,为了防止模型过拟合,正则化惩罚是关键手段。过拟合的本质,是模型在训练集上过度学习,甚至"死记硬背"了数据中的噪声,导致决策边界出现局部异常陡峭的划分。要知道,逻辑回归处理的二分类任务中,两类样本通常存在相对清晰的区分规律,这种过度贴合局部噪声的划分方式,显然会让模型在新数据上的泛化能力大打折扣。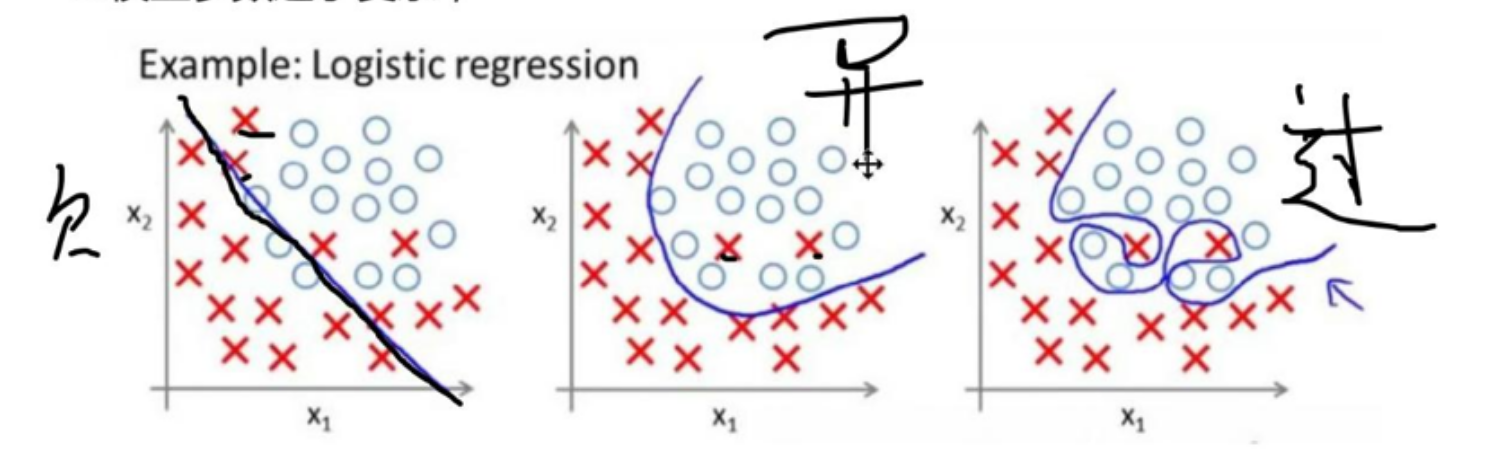
这种"局部异常变化"反映在数学层面,就是模型求解出的参数(权重)绝对值过大。因此正则化惩罚的核心思路,就是在损失函数中加入一个与参数相关的正向项------通过这种"惩罚"机制压缩参数的大小,从根源上避免参数过大导致的过拟合问题。
而正则化因子C,正是调控这份"惩罚力度"的关键旋钮。这里需要明确一个核心逻辑:C的数值与惩罚强度呈正相关,C越大,意味着对参数过大的惩罚越严厉,模型越难出现过拟合;反之,C越小,惩罚力度越弱,模型则更容易陷入过拟合。
但问题来了------到底多大的C才能让模型达到最优准确率?其实并没有固定公式可以直接计算,实践中最可靠的方法是"遍历测试+交叉验证"。我们可以构建一个包含常见C值的候选集合(比如0.01、0.1、1、10、100这类数量级递增的数值),通过循环结构逐一测试,同时结合交叉验证(如5折或10折交叉验证)减少随机误差,最终筛选出在验证集上指标最优的C值。
案例(实现"遍历测试+交叉验证")
我们依旧以银行贷款的项目为例,来讲解具体如何进行"遍历测试+交叉验证"。
实现代码:
python
scores = [] # 不同的c参数在验证集下的评分
c_param_range = [0.01, 0.1, 1, 10, 100] # 参数
for i in c_param_range: # 第1次循环的时候C=0.01,5个逻辑回归模型
lr = LogisticRegression(C=i, penalty='l2', solver='lbfgs', max_iter=1000)
score = cross_val_score(lr, x_train, y_train, cv=8, scoring='recall') # 交叉验证
# scoring:可选"accuracy"(精度)、recall(召回率)、roc_auc(roc值)、neg_mean_square
score_mean = sum(score)/len(score) # 交叉验证后的值召回率
scores.append(score_mean) # 里面保存了所有的交叉验证召回率
print(score_mean) # 将不同的c参数分别传入模型,分别看看哪个模型效果更好,我们选c
best_c = c_param_range[np.argmax(scores)] # 寻找到scores中最大值的对应的C参数
print(f"最好的正则化因子C:{best_c}")原理拆解:
交叉验证的核心逻辑,是利用训练集的特征和标签,计算当前正则化因子C对应的模型得分。它之所以能提升评估可靠性,关键在于解决了"数据排序偏见"问题------比如银行数据可能因不同时间段的营销活动呈现明显差异,若简单划分训练集和验证集,很可能让验证集集中包含某类特殊数据,导致评估结果失真。
具体操作时,我们会把原始训练集拆分为若干组(比如8组),每次选取其中1组作为验证集,剩余7组作为新的训练集。用新训练集训练模型后,在验证集上计算得分;重复这个过程8次,让每组数据都担任过一次验证集,最终取8次得分的平均值,作为该正则化因子C的最终性能得分。通过对比所有候选C值的得分,就能清晰定位到最优参数。
下面附上完整的项目代码,其实仅仅是中间加入了for循环,使用价差验证的方法获取最优的正则化因子C。
python
import pandas as pd
from sklearn.preprocessing import StandardScaler, MinMaxScaler
date=pd.read_csv("creditcard.csv")
scaler_z = StandardScaler() #初始化类
date["Amount"]=scaler_z.fit_transform(date[["Amount"]]) #实现标准化,注意.fit_transform()方法需要二维数据,因此使用双括号
date.drop(columns="Time",inplace=True)#删除列,后面参数表示直接在原表格中删除
from sklearn.model_selection import train_test_split
X = date.drop('Class', axis=1) # 特征集(二维DataFrame)
y = date['Class'] # 标签集(一维Series)
x_train, x_test, y_train, y_test = train_test_split(
X, # 特征集
y, # 标签集
test_size=0.3, # 测试集占比(如0.2表示20%测试集,80%训练集)
random_state=42 # 随机种子(固定值可让每次切分结果一致)
)
#在测试集中进行分成八份的交叉验证,找到最好的正则化惩罚的C,即最好的限制过拟合
import numpy as np
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import cross_val_score
scores = [] # 不同的c参数在验证集下的评分
c_param_range = [0.01, 0.1, 1, 10, 100] # 参数
for i in c_param_range: # 第1次循环的时候C=0.01,5个逻辑回归模型
lr = LogisticRegression(C=i, penalty='l2', solver='lbfgs', max_iter=1000)
score = cross_val_score(lr, x_train, y_train, cv=8, scoring='recall') # 交叉验证
# scoring:可选"accuracy"(精度)、recall(召回率)、roc_auc(roc值)、neg_mean_square
score_mean = sum(score)/len(score) # 交叉验证后的值召回率
scores.append(score_mean) # 里面保存了所有的交叉验证召回率
print(score_mean) # 将不同的c参数分别传入模型,分别看看哪个模型效果更好,我们选c
best_c = c_param_range[np.argmax(scores)] # 寻找到scores中最大值的对应的C参数
print(f"最好的正则化因子C:{best_c}")
lr = LogisticRegression(C=best_c, penalty='l2', solver='lbfgs', max_iter=1000)
lr.fit(x_train,y_train)
#自测,检测欠拟合
y_pre1=lr.predict(x_train)
print(lr.score(x_train,y_train))
from sklearn import metrics
print(metrics.classification_report(y_train, y_pre1,digits=6))
#测试
y_pre=lr.predict(x_test)
print(lr.score(x_test,y_test))
from sklearn import metrics
print(metrics.classification_report(y_test, y_pre,digits=6))参数说明:逻辑回归中penalty='l2'表示使用L2正则化(也是逻辑回归的默认正则化方式,对应 Ridge 回归的惩罚逻辑,能有效压缩参数但不会使参数归零);solver='lbfgs'是适用于L2正则化的优化求解器,在中大型数据集上表现更高效;max_iter=1000则是为了避免模型在复杂数据上因迭代次数不足导致不收敛,根据实际数据情况可灵活调整。
执行结果: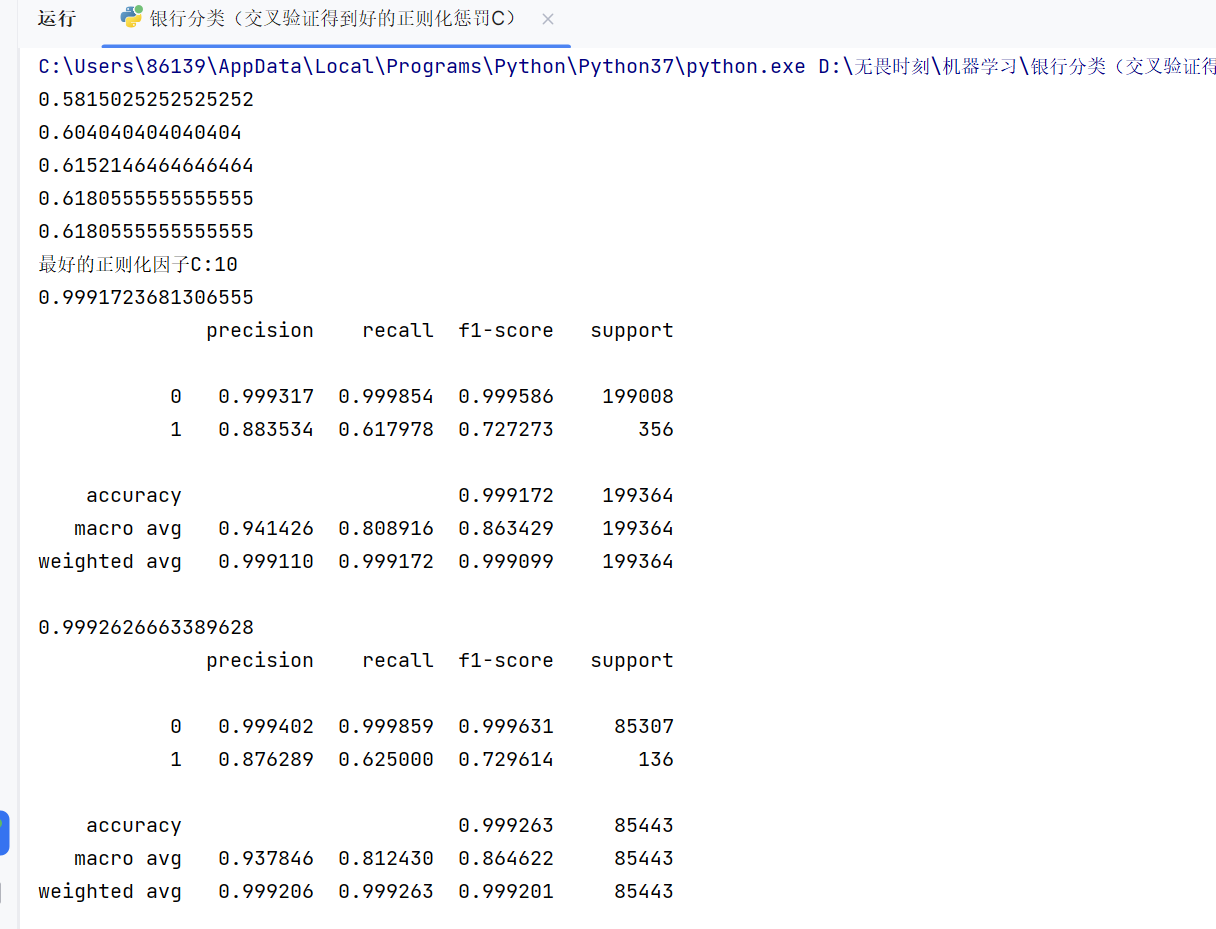
这里我们先用训练集做了一个自测,目的是防止欠拟合。如果测试集的结果比自测还要低,就说明我们的模型欠拟合了。
可以看到我们通过找到最优的正则化因子C的确是提高了我们要求的召回率(之前是0.5左右)。
2、阈值设定
原理:
刚才调整正则化参数的方法,本质是通过压缩模型参数让分类边界更平滑(避免过拟合)。但我们的核心目标是提升召回率(以银行贷款项目为例,要尽可能识别出所有高风险用户)------ 那有没有更直接的方式?
比如,逻辑回归的分类边界本质是一条划分两类样本的线,我们能不能直接把这条线 "往某一类样本的方向偏一偏"?
:
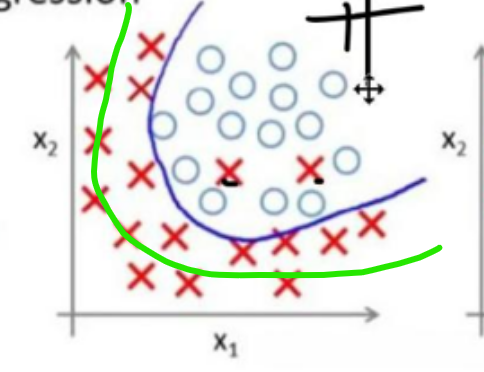
但这种 "人为偏移分类线" 的方法,其实是 "拆东墙补西墙":看似提升了某一类的识别率,却会让另一类的错误率大幅上升,在实际项目中很少用。
具体操作:
回到逻辑回归的分类原理:模型会把样本映射到 sigmoid 函数上,默认以 0.5 为分界点 (sigmoid 输出≥0.5 则预测为正类,否则为负类)。而 "阈值设定" 的核心,就是把这个默认的 0.5 分界点,替换成其他数值(比如 0.1、0.2、0.3)------ 通过调整 sigmoid 函数的划分界限,直接改变模型对 "正类 / 负类" 的判定标准,从而针对性优化召回率等指标。
案例:
代码实现:
python
"""修改逻辑回归中的阈值以最优模型为例"""
#设定阈值
thresholds = [0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9]
recalls = []
for i in thresholds:
y_predict_proba = lr.predict_proba(X_test)
y_predict_proba = pd.DataFrame(y_predict_proba)
y_predict_proba = y_predict_proba.drop([0],axis=1)
y_predict_proba[y_predict_proba[1] > i] = 1 #当预测的概率大于i,0.1,0.2,预测的标签设置1
y_predict_proba[y_predict_proba[1] <= i] = 0 #当预测的概率小于等于i 预测的标签设置为0
# cm_plot(y_test, y_predict_proba[1]).show()
recall = metrics.recall_score(y_test, y_predict_proba[1])
recalls.append(recall)
print("{} Recall metric in the testing dataset: {:.3f}".format(i,recall))这里是显示不同阈值的代码,主体部分和之前的代码没有区别,可自行完成。
运行结果: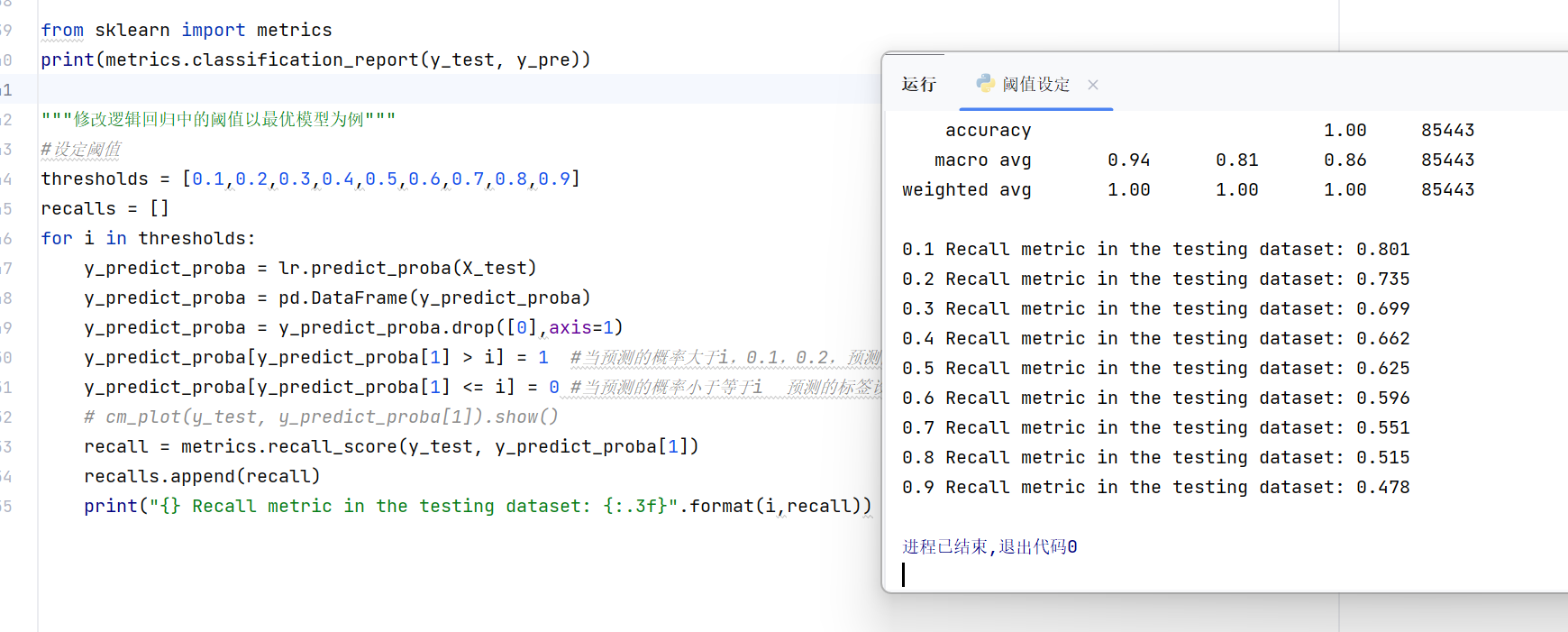
3、数据集平衡
虽然上面这两种方法确实实现了模型的优化,但我不知道大家一直以来有没有注意到一个最基本的问题。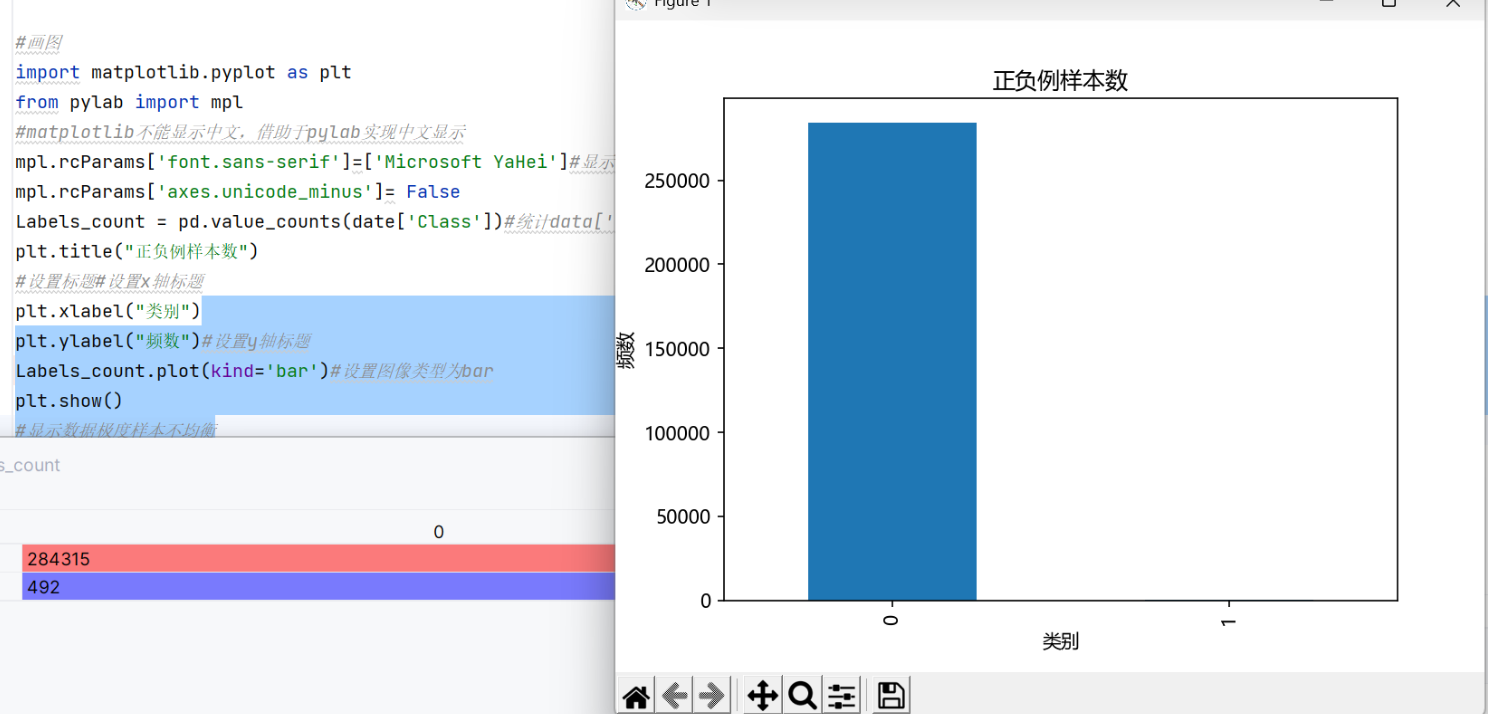
事实上我们的数据是极度不均衡的,基于这种不均衡的数据集训练出来的模型肯定容易产生偏差,我们现在学习两种处理数据集的方法。
欠采集:
原理:
从大量的0类数据中选出和1类数据相同数量的样本来训练模型。
代码实现:
python
from sklearn.model_selection import train_test_split
X = date.drop('Class', axis=1) # 特征集(二维DataFrame)
y = date['Class'] # 标签集(一维Series)
x_train, x_test, y_train, y_test = train_test_split(
X, # 特征集
y, # 标签集
test_size=0.3, # 测试集占比(如0.2表示20%测试集,80%训练集)
random_state=42 # 随机种子(固定值可让每次切分结果一致)
)
#######欠采样处理数据,均衡各类样本
x_train["class"]=y_train #合并
# 1. 假设你已有的样本1的行
df_1 = x_train[x_train["class"] == 1]
# 2. 获取样本1的数量
n_samples = len(df_1)
# 3. 筛选样本0的所有行
df_0 = x_train[x_train["class"] == 0]
# 4. 随机抽取相同数量的0样本
df_0_sample = df_0.sample(n=n_samples, random_state=42)
# 5. 合并得到平衡数据集(可选)
df_balanced = pd.concat([df_1, df_0_sample], axis=0).reset_index(drop=True)
x_train=df_balanced.drop('class', axis=1)
y_train=df_balanced["class"]这里是欠采集数据处理部分的代码,其他代码不变。
运行结果:
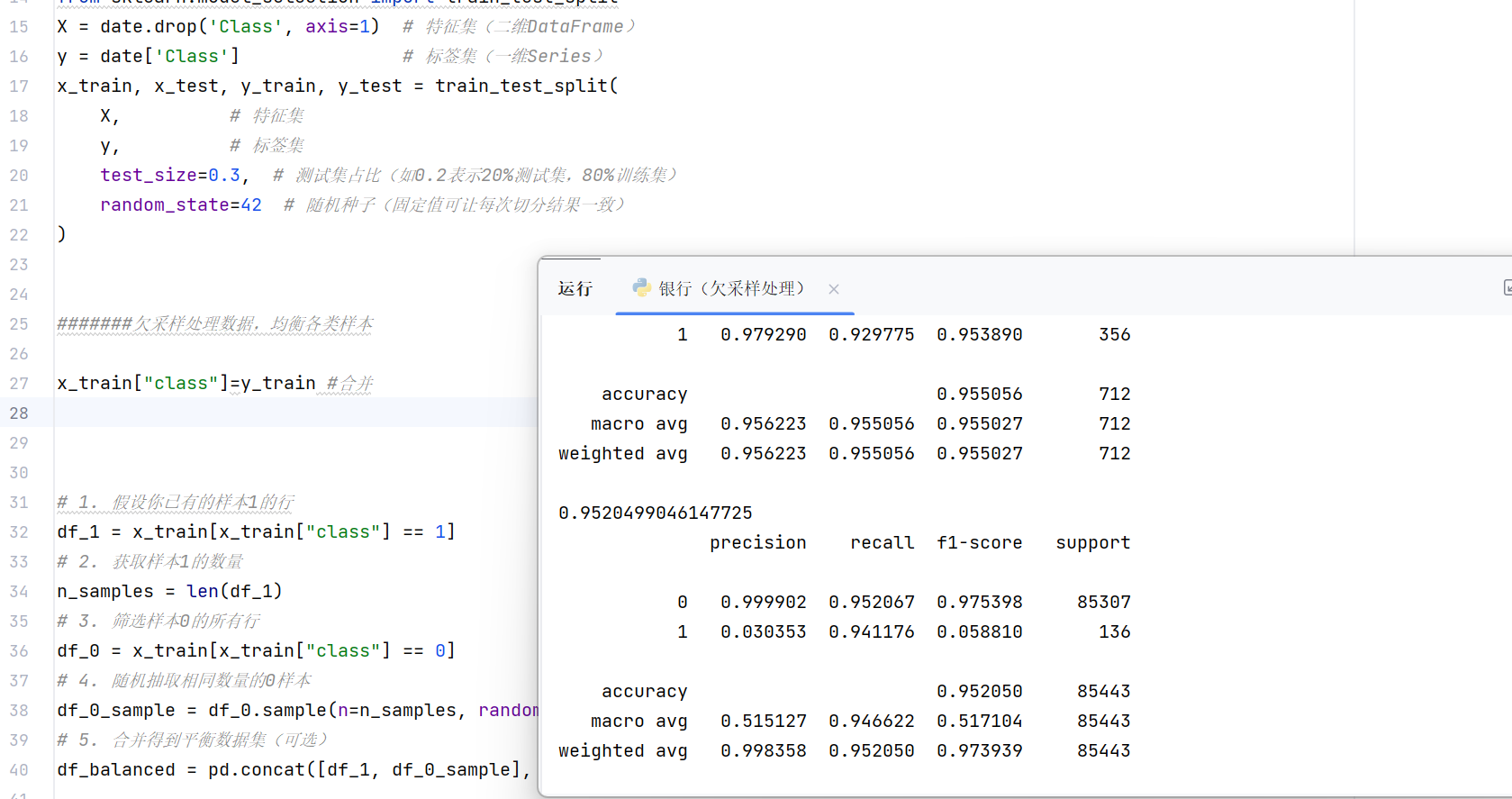
可以看到,我们的召回率显著提高。这说明了数据集的重要性。
过采集:
原理:
造出更多的0类数据
代码实现:
python
from sklearn.model_selection import train_test_split
X = date.drop('Class', axis=1) # 特征集(二维DataFrame)
y = date['Class'] # 标签集(一维Series)
x_train, x_test, y_train, y_test = train_test_split(
X, # 特征集
y, # 标签集
test_size=0.3, # 测试集占比(如0.2表示20%测试集,80%训练集)
random_state=42 # 随机种子(固定值可让每次切分结果一致)
)
#######过采样处理数据,均衡各类样本
# 导入SMOTE过采样工具
from imblearn.over_sampling import SMOTE
# 初始化SMOTE对象,设置随机种子保证结果可复现
smote = SMOTE(random_state=0)
# 对训练集进行SMOTE过采样,生成平衡后的特征和标签
os_x_train, os_y_train = smote.fit_resample(x_train, y_train)这里使用了imlearn第三方库,需要自行安装。