归并排序的简单介绍

基本原理:

归并排序（MERGE-SORT）是建⽴在归并操作上的⼀种有效的排序算法,该算法是采⽤分治法（Divide and Conquer）的⼀个⾮常典型的应⽤。将已有序的⼦序列合并，得到完全有序的序列；即先使每个⼦序列有序，再使⼦序列段间有序。若将两个有序表合并成⼀个有序表，称为⼆路归并.

代码实现:

递归实现:

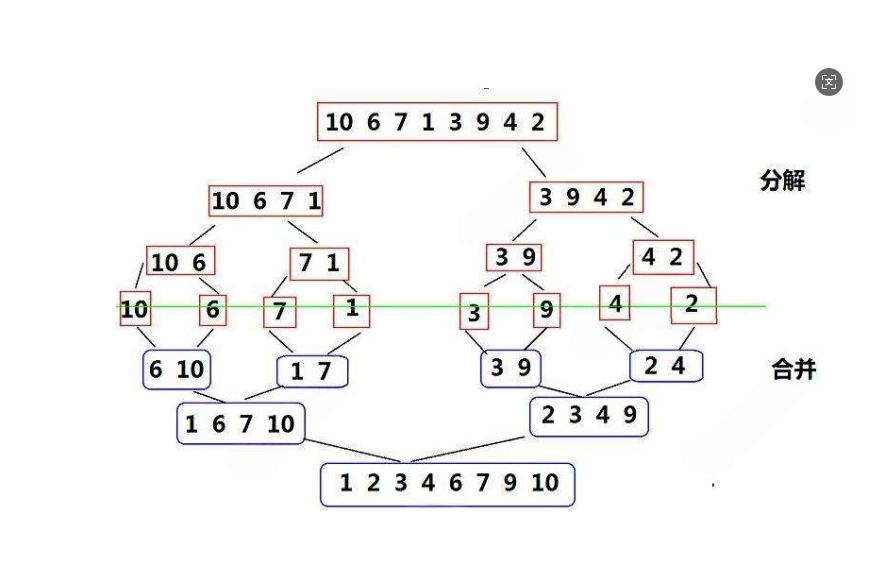
将待排序的元素分为只有一个元素的有序序列, 一步步递归合并最终达到整体有序

代码:

java 复制代码

public static void MergeSort(int[] array,int left,int right){
        //当序列只有2个元素时,mid=0就不需要再分解序列了
        if (left>=right)return;

        int mid = (left+right)/2;
        MergeSort(array,left,mid);
        MergeSort(array,mid+1,right);
        Merge(array,left,right,mid);
    }
    public static void Merge(int[] array,int left, int right,int mid){
        //创建一个新的数组用来放合并后的序列
        //长度是每一次要进行合并序列的总长度
        int[] tempArray= new int[right-left+1];
        //新数组的下标k
        int k = 0;
        //将待合并的序列分为两个部分
        //并表示两个新的序列的开始和结束下标
        int s1 = left;
        int e1 = mid;
        int s2 = mid+1;
        int e2 = right;
        //进行判断,然后将值复制到新数组上
        while (s1 <= e1 && s2 <= e2) {
            if(array[s2] <= array[s1]) {
                //将临时数组赋值后,S2要+1向后判断
                tempArray[k++] = array[s2++];
            }else {
                //同理
                tempArray[k++] = array[s1++];
            }
        }
        //存在一种情况, 当s1或s2的序列全部遍历完, 但另外一个序列还没有动过
        //下面是对于这种情况的处理:
        //当
        while (s1 <= e1) {
            tempArray[k++] = array[s1++];
        }
        while (s2 <= e2) {
            tempArray[k++] = array[s2++];
        }
        //将临时的数组的值覆盖到原来的数组上
        for (int i = 0; i < tempArray.length; i++) {
            array[i+left] = tempArray[i];
        }
    }

非递归实现:

将待排序的元素分为只有一个元素的有序序列, 定义一个变量gap表示每个序列中的元素个数. 利用一个变量i表示每一个序列第一个元素的下标. 之后i遍历第一个元素的下标对此序列进行排序. 然后gap*2, 进行下一轮的排序

代码:

java 复制代码

    private static void MergeSortNormal(int[] array, int left, int right) {
        //gap是每个序列中元素之间的距离,可以看成每个序列有gap个元素
        int gap=1;
        //gap=1时 序列被分为若干组,每组只有一个元素
        while(gap<array.length){
            for (int i = 0; i < array.length; i+=2*gap) {
                int mid =i+gap-1;
                //确定待排序序列的左右边界
                left=i;
                right = i+2*gap-1;
                //判断mid或right是否越界
                //一旦越界就调到数组的最后一个元素
                if(mid>=array.length){
                    mid=array.length-1;
                }
                if(right>=array.length){
                    right=array.length-1;
                }
                Merge(array,left,right,mid);
            }
            //调整每个序列中的元素个数,
            gap=2*gap;
        }
    }

总结

时间复杂度:O(NlogN). 不管最坏还是最好情况都一样. 因为始终都是一直将序列分成2部分,且2部分的元素个数一样.

空间复杂度:O(N). 用到了一个临时数组存放排完序的元素.

是稳定排序