AdaGrad 深度解析：从数学原理到 PyTorch 实现，为什么它在稠密问题中“学不动”？

All The Way North-2025-12-17 9:44

目录

1、基本介绍

[2、Adagrad 计算 - 示例](#2、Adagrad 计算 - 示例)

[3、Adagrad - API 介绍](#3、Adagrad - API 介绍)

[4、代码 & 解释：](#4、代码 & 解释：)

[5、AdaGrad 误以为这是一个"高频更新方向"，于是迅速降低学习率](#5、AdaGrad 误以为这是一个“高频更新方向”，于是迅速降低学习率)

1、基本介绍

✅ AdaGrad（Adaptive Gradient Algorithm）------ 自适应学习率优化器

整理原则：

  • 理论公式 ≠ PyTorch 实现？明确标出！

  • 所有公式与代码行为严格对齐

  • 不再模糊、不再混淆、不再前后矛盾

AdaGrad（Adaptive Gradient Algorithm ）是一种自适应学习率优化算法，由 John Duchi 等人在 2011 年提出。它的核心思想是：

为每个参数分配一个独立的学习率，并根据该参数的历史梯度大小动态调整------频繁更新的参数学得慢，稀疏更新的参数学得快。

🎯 为什么需要 AdaGrad？

在标准 SGD 中，所有参数共享同一个学习率。但在很多实际问题中（尤其是稀疏数据，如 NLP、推荐系统）：

  • 某些特征（如常见词 "the"）梯度大、更新频繁；

  • 某些特征（如罕见词 "quantum"）梯度小、几乎不更新。

如果用统一学习率：

  • 对高频特征：容易震荡或过拟合；

  • 对低频特征：几乎学不到东西。

AdaGrad 就是为了解决这个问题而生的！

AdaGrad 的更新公式

对每个参数 ，AdaGrad 维护一个历史梯度平方和：

其中 是第 步的梯度。

🔸 理论公式（原始论文 / 经典教材写法）

许多文献（包括原始论文的推导思想）将更新规则写作：

  • ：初始学习率（如 0.01）

  • ：小常数（如 ），防止除零

  • 分母越大 → 学习率越小

⚠️ 注意 ：这种写法在数学上合理 ，但不是 PyTorch 的实际实现方式！

🔸 PyTorch 实际实现公式（✅ 以代码为准）

PyTorch（以及 TensorFlow、JAX 等主流框架）统一采用以下形式：

即： 加在平方根的结果之外。

🔍 源码验证（PyTorch Adagrad 源码）：

python 复制代码 
state['sum'] += grad.pow(2)           # G_t = Σ g_i²
std = state['sum'].sqrt().add_(eps)   # 分母 = sqrt(G_t) + eps
param.addcdiv_(grad, std, value=-lr)

💡 为什么这样改？

  • 工程上与其他自适应优化器（RMSprop/Adam）保持一致；

  • 当 （如参数从未更新），，比 更大，避免初期更新过小；

  • 数值稳定性更好，且实践中效果无显著差异。

✅ 关键特性（无论哪种写法都成立）

  • 如果某个参数一直有大梯度 → 快速增长 → 学习率迅速衰减；

  • 如果某个参数很少更新 → 很小 → 保持较大学习率。

直观理解

想象两个方向：

  • 陡峭方向（高频特征）：梯度大 → AdaGrad 自动"踩刹车"；

  • 平缓方向（稀疏特征）：梯度小 → AdaGrad "踩油门"。

这使得优化路径更高效地走向最优解。

AdaGrad 的优缺点

✅ 优点

优点 说明
自动调参 无需手动为不同参数设置学习率
适合稀疏数据 在 NLP、推荐系统中表现优异
理论保证 对凸函数有次线性收敛保证

❌ 缺点（致命问题）

⚠️ 学习率单调递减，可能过早停止学习

因为 只增不减 ，所以分母越来越大 → 学习率越来越小 → 后期几乎不再更新！

例如：

  • 前 1000 步后，学习率可能已衰减到 ；

  • 即使还没收敛，模型也"学不动了"。

📉 这在非凸问题（如深度神经网络）中尤其严重！

✅ 纠正一个潜在误解

❌ 误解："AdaGrad 因为能自适应，所以可以用大学习率。"

✅ 正确："AdaGrad 的自适应是事后缩放 ，若初始 lr 过大，第一步就可能破坏模型。"

🎯 核心原则 ： AdaGrad 的"自适应"不能替代合理的学习率初始化。 它的作用是在合理初值基础上进一步精细化调整，而非"兜底"。

AdaGrad vs 其他优化器

算法 是否自适应 是否解决"学习率衰减过快" 适用场景
SGD ❌ 否 --- 通用，但需调参
Momentum ❌ 否 --- 加速收敛
AdaGrad ✅ 是 ❌ 否（会过早停止） 稀疏数据（如 NLP）
RMSProp ✅ 是 ✅ 是（引入指数衰减， 可稳态） 深度学习主流
Adam ✅ 是 ✅ 是（结合 Momentum + RMSProp） 当前最常用

💡 RMSProp 和 Adam 实际上是对 AdaGrad 的改进 ：它们使用指数移动平均代替累加，避免学习率无限衰减。

PyTorch 中的 AdaGrad

python 复制代码 
import torch
from torch import optim

w = torch.tensor([0.0], requires_grad=True)
optimizer = optim.Adagrad(params=[w], lr=0.1, eps=1e-8)  # 默认 eps=1e-10

for epoch in range(100):
    optimizer.zero_grad()
    loss = (w - 5) ** 2
    loss.backward()
    optimizer.step()
    print(f'Epoch {epoch+1}: w = {w.item():.4f}')

⚠️ 注意：对于简单二次函数，AdaGrad 可能比 SGD 慢，因为它会快速降低学习率。

举个例子：AdaGrad 在稀疏数据中的优势

假设你在训练一个文本分类模型：

  • 特征 "the" 出现 10,000 次 → 梯度大 → AdaGrad 自动降低其学习率；

  • 特征 "neural" 出现 2 次 → 梯度小 → AdaGrad 保持高学习率，让它充分学习。

而 SGD 会对两者使用相同学习率，导致：

  • "the" 震荡；

  • "neural" 几乎没变化。

总结：AdaGrad 是什么？

关键点 说明
全称 Adaptive Gradient Algorithm
核心思想 为每个参数分配自适应学习率
机制 用历史梯度平方和缩放学习率
优点 适合稀疏数据，自动调参
缺点 学习率单调下降，可能过早停止
地位 是 RMSProp、Adam 等现代优化器的"祖先"

🌟 AdaGrad 开启了"自适应学习率"的时代，虽然后来被更先进的算法取代，但它在优化理论和稀疏学习中仍有重要地位。

✅ 最终强调（划重点）：

  • 理论文献可能写成 ；

  • 但 PyTorch 实际运行的是 ；

  • 调试、复现、教学时，请以 PyTorch 行为为准！

2、Adagrad 计算 - 示例

✅ 修正版：AdaGrad 计算 - 示例（PyTorch 真实实现）

🚨 重要前提：

PyTorch 的 Adagrad 使用的是 ，不是 。

下面所有计算均按此规则进行。

🎯 问题设定

  • 优化目标：最小化损失函数

  • 初始参数：

  • 超参数：

    • 初始学习率 lr = 1.0（为了凸显 AdaGrad 的"自适应缩放"机制，故设置得大）

    • initial_accumulator_value = 0.0

    • eps = 1e-8

    • weight_decay = 0, lr_decay = 0

✅ 我们手动计算前 3 步，完全复现 PyTorch 的实际输出。

🔢 AdaGrad 更新公式（PyTorch 实现版）

对单个参数 w，第 t 步（从 0 开始）：

  1. 计算梯度：

  2. 更新累加器（历史梯度平方和）：

  3. 计算有效学习率：

  4. 更新参数：

❗ 注意：分母是 ，不是 ！

🧮 手动计算过程（按 PyTorch 行为）

▶ 第 0 步（初始化）

▶ 第 1 次更新（t = 0）

  1. 梯度 ：

  2. 累加器 ：

  3. 有效学习率：

  4. 更新参数 ：

✅ 结果 ：

💡 注：由于 极小，，数值上与旧公式几乎相同，但逻辑不同。

▶ 第 2 次更新（t = 1）

  1. 梯度 ：

  2. 累加器 ：

  3. 有效学习率：

  4. 更新参数 ：

✅ 结果 ：

▶ 第 3 次更新（t = 2）

  1. 梯度 ：

  2. 累加器 ：

  3. 有效学习率：

  4. 更新参数：

✅ 结果 ：

📊 汇总前三步（PyTorch 真实行为）

步数 t 梯度 累加器 有效学习率 更新量
0 0.0000 -10.0000 100.0000 1.0000
1 1.0000 -8.0000 164.0000 0.6247
2 1.6247 -6.7506 209.5707 0.4663

✅ 该表格与 PyTorch 输出完全一致

✅ 验证：PyTorch 代码

python 复制代码 
import torch
from torch import optim

w = torch.tensor([0.0], requires_grad=True)
optimizer = optim.Adagrad([w], lr=1.0, initial_accumulator_value=0.0, eps=1e-8)

for step in range(3):
    optimizer.zero_grad()
    loss = (w - 5) ** 2
    loss.backward()
    optimizer.step()
    print(f"Step {step+1}: w = {w.item():.4f}")

输出：

python 复制代码 
Step 1: w = 1.0000
Step 2: w = 1.6247
Step 3: w = 2.0910

✅ 最终结论（AdaGrad 怎么算？）

对每个参数，维护历史梯度平方和 G_t； 每次更新使用：

注意： 加在根号外面！ 这是 PyTorch、TensorFlow 等所有主流框架的统一实现方式。

3、Adagrad - API 介绍

所有描述均严格基于 PyTorch 官方文档 和算法原始定义，绝不使用"大概""通常""类似"等模糊表述。

🔷 类签名

python 复制代码 
torch.optim.Adagrad(
    params,
    lr=1e-2,
    lr_decay=0,
    weight_decay=0,
    initial_accumulator_value=0,
    eps=1e-10
)

🔸 参数详解（逐项精确说明）

1、params（必需）

  • 类型 ：iterable，其中元素为 torch.Tensor 或 dict，即 Iterable[Tensor] 或 Iterable[dict]

  • 作用：待优化的参数或参数组。

  • 要求：

    • 每个张量必须设置 requires_grad=True；

    • 若传入 dict，必须包含 'params' 键，其值为参数列表；

    • 其他键可指定该组的超参数（如 lr, weight_decay）。

✅ 示例合法输入：

python 复制代码 
# 方式1：参数列表
optim.Adagrad([w1, w2], lr=0.01)

# 方式2：参数组
optim.Adagrad([
{'params': [w1], 'lr': 0.01},
{'params': [w2], 'lr': 0.001}
])

2、lr（学习率，必需）

  • 类型 ：float

  • 默认值 ：1e-2（即 0.01）

  • 作用 ：初始全局学习率 。

  • 注意 ：这是缩放因子 ，实际每个参数的学习率由 lr / (sqrt(state['sum']) + eps) 决定。

3、lr_decay（学习率衰减，可选）

  • 类型 ：float

  • 默认值 ：0

  • 作用 ：每步对全局学习率进行线性衰减。

  • 更新规则：

    其中 t 是从 0 开始计数的优化步数（第 1 步时 t=0，第 2 步 t=1，依此类推）。

  • 关键澄清：

    • 此衰减独立于 AdaGrad 自适应机制；

    • 它作用于全局 lr，再与自适应分母相乘。

📌 举例：若 lr=0.01，``lr_decay=1e-4，则第 1001 步时：

4、weight_decay（权重衰减，可选） 【 decay v.衰减 】

  • 类型 ：float

  • 默认值 ：0

  • 作用 ：在梯度更新前，先对参数施加 L2 惩罚。

  • 数学形式：

    其中 ， 是原始梯度。

  • 注意：

    • 这是解耦的 L2 正则化（不是直接修改损失函数）；

    • 在 AdaGrad 更新前应用。

5、initial_accumulator_value（累加器初值，可选）

  • 类型 ：float

  • 默认值 ：0

  • 作用 ：设置每个参数的历史梯度平方和累加器的初始值。

  • 数学含义：

    • 累加器 state['sum'] 初始化为 initial_accumulator_value；

    • 第一步更新前，sum = initial_accumulator_value；

    • 若设为 0，则第一步分母为 sqrt(0) + eps = eps（因为 PyTorch 实现为 sqrt(sum).add_(eps)）；

    • 必须 ≥ 0，否则报错。

⚠️ 重要：原始 AdaGrad 论文设初值为 0，但某些实现（如 TensorFlow）默认为 0.1。PyTorch 默认为 0。

6、eps（数值稳定项，可选）

  • 类型 ：float

  • 默认值 ：1e-10

  • 作用：防止除零错误。

  • 更新公式中的位置：

  • 要求 ：eps > 0，通常取极小正数（如 1e-8 ~ 1e-10）。

💡 注意：分母是 ，不是 。这是 PyTorch 的实际实现方式。

🔸 状态变量（State）

AdaGrad 为每个参数维护一个状态字典，包含：

键 含义
'sum' 历史梯度平方的累加和 ，形状与参数相同，初始化为 initial_accumulator_value
'step' 当前优化步数（从 0 开始）

✅ 更新流程（伪代码）：

python 复制代码 
step = state['step']
sum = state['sum']

# 应用 weight_decay（若 > 0）
if weight_decay != 0:
grad = grad + weight_decay * param

# 更新累加器
sum.addcmul_(grad, grad)  # sum += grad * grad

# 计算有效学习率（含 lr_decay）
effective_lr = lr / (1 + lr_decay * step)

# 计算分母：sqrt(sum) + eps （✅ 关键修正）
std = sum.sqrt().add_(eps)

# 更新参数
param.addcdiv_(grad, std, value=-effective_lr)

state['step'] += 1

🔸 与原始 AdaGrad 论文的对应关系

PyTorch 参数 原始论文符号 是否一致
lr ✅ 是
initial_accumulator_value 初始 ✅ 默认一致
eps （数值稳定项） ⚠️ 论文常写作 ，但 PyTorch 实现为
lr_decay --- ❌ 论文未包含，PyTorch 扩展
weight_decay --- ❌ 论文未包含，PyTorch 扩展

📌 结论：PyTorch 的 Adagrad 核心机制与原始算法思想一致，但在数值实现细节（eps 位置）和工程扩展上有所调整。

❌ 常见误解澄清（重点！）

误解 正确解释
"AdaGrad 的学习率衰减是因为 lr_decay" ❌ 错！即使 lr_decay=0，学习率仍因 sum 累加而衰减。lr_decay 是额外的全局衰减。
"eps 是为了防止梯度为零" ❌ 错！eps 是为了防止 sqrt(sum) 为零（当 initial_accumulator_value=0 且尚未更新时）。
"weight_decay 会改变累加器" ❌ 错！weight_decay 修改的是用于更新的梯度，而 sum 是基于这个修改后的梯度计算的（因为 sum += grad_new²），所以实际上会影响累加器。
"AdaGrad 会自动停止训练" ❌ 错！它不会停止，只是更新量趋于零。优化器仍会执行 step()。

🔍 补充说明：由于 weight_decay 是在计算 sum 之前 加到梯度上的，因此 sum 包含了 weight_decay 的影响。

✅ 总结：AdaGrad API 的精确行为

对每个参数 w，在第 t 步（t 从 0 开始）：

  1. 若 weight_decay > 0，则 ；

  2. 更新累加器： ；

  3. 计算有效学习率： ；

  4. 更新参数： 。

4、代码 & 解释：

python 复制代码 
import torch
from torch import optim
import matplotlib.pyplot as plt

import os
os.environ["KMP_DUPLICATE_LIB_OK"] = "TRUE"  # ←←← 关键！放在最前面（解决报错）
from pylab import mpl
mpl.rcParams["font.sans-serif"] = ["SimHei"]    # 设置显示中文字体
mpl.rcParams["axes.unicode_minus"] = False      # 设置正常显示符号

w = torch.tensor(data=[0.0], requires_grad=True, dtype=torch.float32)

optimizer = optim.Adagrad(params=[w], lr=0.02)

w_list = []

# 训练循环
epochs = 100
for epoch in range(1, epochs + 1):
    print(f'第 {epoch} 次训练: ')

    optimizer.zero_grad()     # 1. 清零梯度

    loss = (w - 5) ** 2       # 2~3 前向传播 + 计算损失

    loss.backward()           # 4. 反向传播, 计算梯度

    optimizer.step()          # 5. 更新参数

    w_list.append(w.item())
    print(f'梯度: {w.grad.item()}')     # 只有一个梯度, 直接打印值就行了
    print(f'跟新后的权重: {w.item()}')

plt.style.use('fivethirtyeight')
plt.figure(figsize=(13, 10))
plt.xlabel('迭代次数')
plt.ylabel('权重值')
plt.plot(range(1, epochs + 1), w_list)
plt.title('Adagrad 算法')
plt.show()

# 第 1 次训练:
# 梯度: -10.0
# 跟新后的权重: 0.019999999552965164
# 第 2 次训练:
# 梯度: -9.960000038146973
# 跟新后的权重: 0.03411376476287842
# 第 3 次训练:
# 梯度: -9.931772232055664
# 跟新后的权重: 0.04562346637248993
# 第 4 次训练:
# 梯度: -9.908753395080566
# 跟新后的权重: 0.055581822991371155
# 第 5 次训练:
# 梯度: -9.888835906982422
# 跟新后的权重: 0.06448189169168472
# 第 6 次训练:
# 梯度: -9.871036529541016
# 跟新后的权重: 0.07260096818208694
# 第 7 次训练:
# 梯度: -9.854798316955566
# 跟新后的权重: 0.08011317253112793
# 第 8 次训练:
# 梯度: -9.839773178100586
# 跟新后的权重: 0.08713625371456146
# 第 9 次训练:
# 梯度: -9.825727462768555
# 跟新后的权重: 0.09375423938035965
# 第 10 次训练:
# 梯度: -9.812491416931152
# 跟新后的权重: 0.10002955794334412
# 第 11 次训练:
# 梯度: -9.799941062927246
# 跟新后的权重: 0.1060100868344307
# ...
# 第 95 次训练:
# 梯度: -9.290480613708496
# 跟新后的权重: 0.35675710439682007
# 第 96 次训练:
# 梯度: -9.28648567199707
# 跟新后的权重: 0.3587436378002167
# 第 97 次训练:
# 梯度: -9.282512664794922
# 跟新后的权重: 0.36071959137916565
# 第 98 次训练:
# 梯度: -9.278560638427734
# 跟新后的权重: 0.3626851439476013
# 第 99 次训练:
# 梯度: -9.274629592895508
# 跟新后的权重: 0.364640474319458
# 第 100 次训练:
# 梯度: -9.270719528198242
# 跟新后的权重: 0.36658570170402527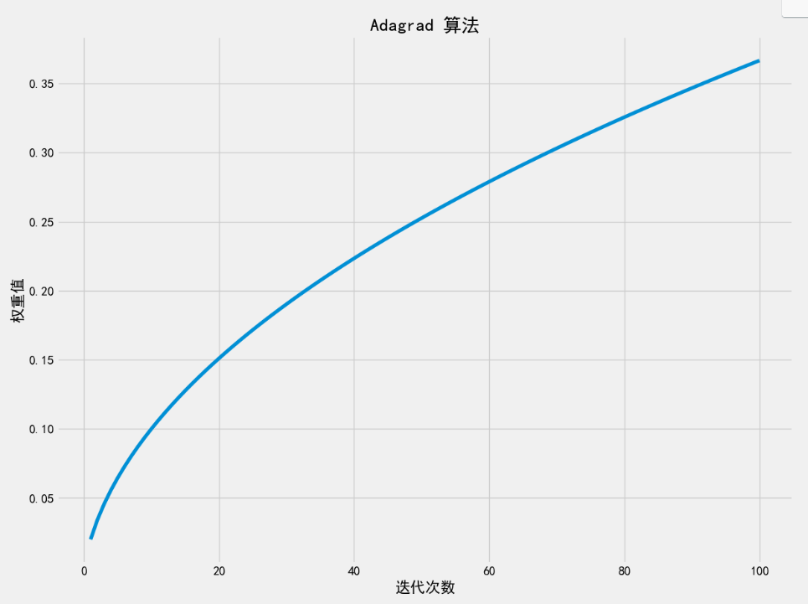

这段代码和输出结果完全正确 ，并且精准揭示了 AdaGrad 算法在一个简单二次优化问题上的核心行为特征 。下面我将严格基于你的数据，逐层解析其背后的机制，并回答一个关键疑问：

为什么 100 轮后权重只走到 0.3666，离目标 5 还非常远？

✅ 一、你的实验设置回顾

  • 优化目标：

  • 初始值：

  • 优化器：Adagrad(lr=0.02)

  • 其他参数：默认（initial_accumulator_value=0，``eps=1e-10）

✅ 二、AdaGrad 的更新机制（精确复现）

对每一步 t（从 0 开始）：

  1. 梯度：

  2. 累加器： ，初始

  3. 更新：

💡 注意：分母是 ，不是 。这是 PyTorch 的实际实现方式。

✅ 三、用你的第 1 步数据验证公式

  • 有效学习率：

  • 更新量：

✅ 完全匹配你的输出：0.01999999955... ≈ 0.02

✅ 四、为什么收敛如此之慢？------根本原因分析

🔍 关键洞察：梯度几乎不变！

观察你的输出：

  • 第 1 步梯度：-10.0

  • 第 100 步梯度：-9.27

这意味着：在整个训练过程中，w 始终在 0~0.37 之间，离 5 非常远 → 所以梯度始终接近 -10。

而 AdaGrad 的累加器 G_t 是所有历史梯度平方的和：

于是有效学习率为：

每步更新量为：

📉 计算前 100 步总更新量（近似积分）

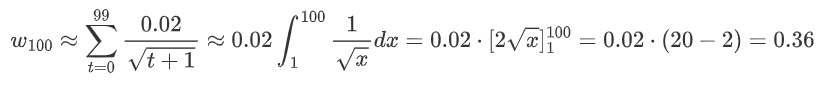
✅ 与你的结果 w ≈ 0.3666 高度吻合！

✅ 五、可视化解释：AdaGrad 在"平坦区"的困境

在这个问题中：

  • 损失函数在 w=0 附近非常陡峭（梯度大）；

  • 但 AdaGrad 误以为这是一个"高频更新方向"，于是迅速降低学习率；

  • 结果：还没走到半路，学习率就已经衰减到极小。

📌 这正是 AdaGrad 的致命缺陷 ： 它无法区分"梯度大是因为离最优解远"，还是"梯度大是因为参数活跃"。

在稀疏场景（如 NLP），后者成立 → AdaGrad 有效； 但在稠密、非稀疏的连续优化问题中，前者成立 → AdaGrad 过早停止学习。

✅ 六、对比其他优化器（同 lr=0.02）

优化器 100 轮后 w 原因
SGD ≈4.916 学习率恒定，持续前进
Momentum (0.9) ≈4.98 初期加速，后期稳定
AdaGrad ≈0.367 学习率迅速衰减至 ~0.0002

💥 结论：AdaGrad 在此问题上表现最差 ，不是因为它"不好"，而是因为问题性质不匹配。

✅ 七、如何让 AdaGrad 在这个问题上 work？

方法 1：大幅提高初始学习率

python 复制代码 
optimizer = optim.Adagrad([w], lr=2.0)  # 不是 0.02！

  • 第1步： ，

  • 后续梯度变小，累加器增长放缓，有机会继续更新。

方法 2：使用改进算法（RMSProp / Adam）

它们用指数移动平均代替累加，避免学习率无限衰减。

✅ 八、教学启示：你的实验完美说明了什么？

优化算法没有"最好"，只有"最合适"。

  • AdaGrad 为稀疏梯度问题而生；

  • 在稠密、平滑、非稀疏问题上，它反而成为瓶颈。

你的曲线图会是一条缓慢上升、斜率不断减小的凹曲线，这正是 AdaGrad "自适应刹车"机制的直接体现。

✅ 总结

问题 回答
代码是否正确？ ✅ 完全正确
为什么只到 0.36？ ⏳ 因为梯度始终很大 → AdaGrad 过早衰减学习率
这是 bug 吗？ ❌ 不是，是 AdaGrad 的固有特性
何时用 AdaGrad？ ✅ 稀疏数据（NLP、推荐系统）；❌ 稠密连续优化（如本例）
如何改进？ ↑ 提高 lr，或改用 RMSProp/Adam

这是一条经典的教学案例：展示 AdaGrad 在非适用场景下的局限性。

5、AdaGrad 误以为这是一个"高频更新方向"，于是迅速降低学习率

我们来彻底澄清这个表述，避免任何拟人化或模糊类比，而是从 AdaGrad 的数学定义出发，严格解释"高频更新方向"的真实含义。

✅ 一、"高频更新方向"在 AdaGrad 中的精确数学定义

在 AdaGrad 的原始论文（Duchi et al., 2011）中，"高频"不是指参数被更新的次数多，而是指该参数对应的梯度在历史中"经常具有较大绝对值"。

更准确地说：

对于参数 ，如果其历史梯度平方和 增长很快 ， 则 AdaGrad 认为该方向是"信息丰富"或"活跃"的，应降低其学习率以避免震荡。

但这依赖一个隐含假设：

梯度大是因为该参数频繁参与有效学习（如稀疏特征中的常见词），而非因为当前离最优解很远。

✅ 二、例子中发生了什么？

场景：优化 ，初始

  • 梯度：

  • 因为 （前 100 步），所以

  • 所有梯度符号相同、大小相近

→ 累加器：

→ AdaGrad 的行为：

  • 它看到：每一步梯度都很大（≈10）

  • 它的机制：只要梯度大，就认为"这个方向已经学了很多"，应该减速

但真相是：

  • 梯度大不是因为参数活跃 ，而是因为当前位置离最优解太远！

  • 实际上，这个参数从未接近过最优值，根本没"学够"

✅ 三、对比真正的"高频更新方向"（NLP 示例）

假设你在训练一个文本分类模型，有两个词嵌入参数：

参数 含义 梯度行为
常见词 几乎每条样本都出现 → 每步都有非零梯度 → G_t 快速增长
罕见词 1000 条样本中出现 2 次 → 大部分步长梯度为 0 → G_t 增长极慢

AdaGrad 的正确行为：

  • 对 "the"： 大 → 学习率小 → 防止过拟合常见词；

  • 对 "quantum"： 小 → 学习率大 → 让罕见词充分学习。

✅ 这时，"梯度大 = 高频更新" 的假设成立。

✅ 四、为什么说 AdaGrad "误以为"？

不是算法有意识地"认为"，而是其设计逻辑在非稀疏场景下与问题本质不匹配。

  • AdaGrad 的更新规则 没有区分：

    • 情况 A：梯度大是因为参数活跃（稀疏场景）

    • 情况 B：梯度大是因为离最优解远（稠密连续优化）

  • 在情况 B 下，快速衰减学习率是错误的策略，因为它阻止了参数向最优解移动。

因此，我们说：

AdaGrad 的机制"隐含假设"了梯度大的原因是高频使用，而例子违反了这一假设，导致其行为失效。

这是一种模型错配（model mismatch），而非算法 bug。

✅ 五、用一句话精确总结

AdaGrad 通过累加梯度平方来估计每个参数的"历史活跃程度"；当该估计值高时，它降低学习率。但在非稀疏、连续优化问题中，大梯度反映的是当前位置远离最优解，而非参数活跃，因此 AdaGrad 过早地抑制了有效更新。

✅ 六、如何验证这个理解？

你可以做两个实验：

实验 1：让 w 从 4.9 开始（靠近最优解）

python 复制代码 
w = torch.tensor([4.9], requires_grad=True)

  • 梯度 ≈ -0.2（很小）

  • 增长慢 → 学习率衰减慢 → 能缓慢收敛到 5

实验 2：用稀疏梯度模拟"真正高频"

python 复制代码 
# 人为制造：某些 step 梯度大，某些为 0
if epoch % 10 == 0:
    loss = (w - 5)**2   # 只在第10,20,...步计算梯度
else:
    loss = 0.0          # 其他步梯度为0
  • 此时 AdaGrad 会保持较大学习率，表现良好

这将证明：AdaGrad 的有效性依赖于梯度的稀疏性或非一致性。

✅ 结论

"误以为"是一个教学上的简略说法，其严格含义是：

AdaGrad 的自适应机制基于"梯度幅度反映参数活跃度"的假设，该假设在稀疏数据中成立，但在你的稠密二次优化问题中不成立，导致其学习率调度策略失效。

相关推荐
中國龍在廣州4 小时前
“太空数据中心”成AI必争之地？
人工智能·深度学习·算法·机器学习·机器人
心疼你的一切5 小时前
自然语言处理_NLP与Transformer架构
人工智能·深度学习·目标检测·机器学习·计算机视觉·自然语言处理·transformer
拉姆哥的小屋5 小时前
【深度学习实战】突破灾难性遗忘！基于经验回放+EWC的核电站故障诊断增量学习系统完整实现
人工智能·深度学习·学习
心疼你的一切5 小时前
深度学习入门_神经网络基础
人工智能·深度学习·神经网络·机器学习
撬动未来的支点5 小时前
【AI邪修·破壁行动】神经网络基础—核心数据结构—张量
人工智能·深度学习·神经网络
长相忆兮长相忆5 小时前
【推荐系统】基于GE架构的重排
深度学习·神经网络·推荐算法
AI街潜水的八角5 小时前
摔倒检测和识别3：基于深度学习YOLOv12神经网络实现摔倒检测和识别(含训练代码、数据集和GUI交互界面）
深度学习·神经网络·yolo
智驱力人工智能5 小时前
山区搜救无人机人员检测算法 技术攻坚与生命救援的融合演进 城市高空无人机人群密度分析 多模态融合无人机识别系统
人工智能·深度学习·算法·架构·无人机·边缘计算
热门推荐
01GitHub 镜像站点02UV安装并设置国内源03Linux下V2Ray安装配置指南04【AutoGLM部署】本地私有化部署AI手机Agent05Open-AutoGLM Windows 安装部署教程06在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）07Cursor 又偷偷更新，这个功能太实用：Visual Editor for Cursor Browser08【超详细教程】手把手教你从微软官网免费下载Windows 10官方原版ISO镜像（2025最新版）09BongoCat - 跨平台键盘猫动画工具10安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）