从400维向量到160000维矩阵：基于深度学习的火焰参数预测系统全解析

从400维向量到160000维矩阵：基于深度学习的火焰参数预测系统全解析资源-CSDN下载

一、引言：当AI遇见火焰科学

在燃烧科学与工程领域，准确预测火焰参数分布是优化燃烧效率、降低污染物排放的关键。传统方法依赖复杂的物理建模和数值仿真，计算成本高、耗时长。本项目提出一种基于深度学习的端到端预测方案：仅输入400维行和向量，即可预测完整的400×400火焰矩阵，将160000个参数的高维预测问题转化为智能化的数据驱动任务。

本文将深入解析该系统的设计思路、技术实现与优化策略，涵盖从数据加载到模型部署的全流程，并提供可复现的代码与实验分析。

---

二、问题定义：从约束到创新

2.1 核心挑战

给定一个400×1的行和向量 v（每行元素之和），预测对应的400×400矩阵 M，满足：

• 约束条件：M 的每一行和等于 v 的对应元素

• 预测精度：矩阵元素分布需接近真实火焰参数分布

• 数值稳定性：处理大动态范围（可能跨越多个数量级）

2.2 技术难点

1. 维度扩展：从400维到160000维，扩展比400:1

1. 约束保证：确保每行和严格等于输入值

1. 分布学习：学习行和到行内分布的复杂映射关系

1. 数值稳定性：避免softmax溢出和梯度爆炸

---

三、技术架构：多模型融合的智能预测系统

3.1 系统整体架构

输入层 (400维行和向量)

↓

特征增强层 (统计特征提取)

↓

Transformer编码器 (注意力机制)

↓

残差网络 (深度特征提取)

↓

输出层 (160000维logits)

↓

Softmax归一化 (行内概率分布)

↓

矩阵重构 (行和约束应用)

↓

输出 (400×400预测矩阵)

3.2 核心模型设计

3.2.1 EnhancedFlameNet：增强型火焰预测网络

这是项目的核心模型，融合多项先进技术：

1. 特征增强模块

def _add_stat_features(self, x):

"""添加统计特征：均值、方差、最大值、最小值、总和"""

mean = x.mean(dim=1, keepdim=True)

var = x.var(dim=1, keepdim=True)

max_val = x.max(dim=1, keepdim=True)[0]

min_val = x.min(dim=1, keepdim=True)[0]

sum_val = x.sum(dim=1, keepdim=True)

stat_features = torch.cat([mean, var, max_val, min_val, sum_val], dim=1)

x_enhanced = torch.cat([x, stat_features], dim=1) # 400 → 405维

return x_enhanced

设计思路：

• 统计特征提供全局信息，帮助模型理解数据分布

• 均值反映整体水平，方差反映离散程度

• 极值信息有助于处理异常情况

2. StableAttention：稳定的多头注意力机制

class StableAttention(nn.Module):

"""稳定的注意力机制：用于捕捉行和向量之间的关系"""

def init(self, dim: int, num_heads: int = 8, dropout: float = 0.1):

super().init()

self.num_heads = num_heads

self.head_dim = dim // num_heads

self.scale = 1.0 / math.sqrt(self.head_dim) # 缩放因子防止梯度爆炸

self.qkv = nn.Linear(dim, dim * 3)

self.proj = nn.Linear(dim, dim)

self.norm = nn.LayerNorm(dim)

self.dropout = nn.Dropout(dropout)

关键技术点：

• 缩放点积注意力：scale = 1/√d_k 防止内积过大

• 残差连接：保证梯度流动

• LayerNorm：稳定训练过程

• Dropout：防止过拟合

3. ResidualBlock：深度网络的基石

class ResidualBlock(nn.Module):

"""残差块：帮助梯度流动，提高表达能力"""

def forward(self, x):

residual = x

x = self.norm1(x)

x = F.gelu(self.linear1(x)) # GELU比ReLU更平滑

x = self.dropout(x)

x = self.linear2(x)

x = self.dropout(x)

x = self.norm2(x)

x = x + residual # 残差连接

return x

为什么使用GELU？

• GELU（Gaussian Error Linear Unit）在负值区域有平滑的非零梯度

• 相比ReLU，GELU能更好地处理梯度消失问题

• 在Transformer架构中表现优异

4. 行归一化约束：核心创新

数值稳定：减去每行的最大值，避免 softmax 溢出

logits = logits - logits.max(dim=-1, keepdim=True).values

Softmax 得到每行的概率分布

row_dist = F.softmax(logits, dim=-1) # (batch, 400, 400)，每行和为 1

用原始行和构造矩阵（关键：保证行和约束）

matrix_pred = row_dist * x.unsqueeze(-1) # (batch, 400, 400)

这是整个系统的核心创新：

• 先学习行内分布（概率形式），再乘以行和得到实际值

• 数学上严格保证：sum(matrix_pred[i, :]) = x[i]

• 将约束优化问题转化为无约束的概率学习问题

3.2.2 SimpleMLP：轻量级基线模型

作为对比基线，SimpleMLP采用全连接网络架构：

class SimpleMLP(nn.Module):

"""简单的MLP模型：快速验证和对比"""

def init(self, input_dim: int = 400, hidden_dim: int = 512, num_layers: int = 3):

多层全连接 + LayerNorm + ReLU

输出层：400*400个logits

特点：

• 参数量小，训练快速

• 适合快速原型验证

• 作为性能对比的baseline

---

四、损失函数设计：多目标优化的艺术

4.1 组合损失函数

def compute_loss(matrix_pred, row_dist_pred, matrices, vectors, use_huber=True):

"""改进的损失函数：结合多种损失以提高精度"""

1. 矩阵重构损失（主要损失）

if use_huber:

loss_matrix = F.huber_loss(matrix_pred, matrices, delta=1.0)

else:

loss_matrix = F.mse_loss(matrix_pred, matrices)

2. MAE 损失（对异常值更鲁棒）

loss_mae = F.l1_loss(matrix_pred, matrices)

3. 行分布损失（确保概率分布正确）

row_sums = matrices.sum(dim=-1, keepdim=True).clamp_min(1e-6)

target_row_dist = matrices / row_sums

loss_dist = F.mse_loss(row_dist_pred, target_row_dist)

4. 行和约束损失（确保每行和等于输入向量）

pred_row_sums = matrix_pred.sum(dim=-1)

loss_row_sum = F.mse_loss(pred_row_sums, vectors)

5. 相对误差损失（对大值和小值都敏感）

relative_error = torch.abs(matrix_pred - matrices) / (matrices.abs() + 1e-6)

loss_relative = relative_error.mean()

组合损失（可调权重）

loss = (

loss_matrix * 1.0 + # 主要损失

loss_mae * 0.3 + # MAE 辅助

loss_dist * 0.2 + # 行分布约束

loss_row_sum * 0.1 + # 行和约束

loss_relative * 0.1 # 相对误差

)

4.2 损失函数设计原理

1. Huber Loss：结合MSE和MAE优点

• 小误差时类似MSE（二次），大误差时类似MAE（线性）

• 对异常值更鲁棒，训练更稳定

1. 行分布损失：学习正确的概率分布

• 即使行和正确，分布也可能错误

• 直接约束概率分布，提高预测质量

1. 行和约束损失：双重保险

• 虽然模型设计已保证行和，但显式约束可进一步强化

• 权重较小（0.1），避免过度约束

1. 相对误差损失：处理大动态范围

• 对大值和小值都敏感

• 避免模型只关注大值而忽略小值

---

五、数据加载与预处理：工程实践的精髓

5.1 数据加载器设计

class FlameDataLoader:

"""火焰数据加载器"""

def load_all_data(self) -> Tuple[np.ndarray, np.ndarray]:

"""加载所有数据并验证一致性"""

pairs = self.get_file_pairs()

vectors = []

matrices = []

for vf, mf in pairs:

vec = self.load_single_vector(vf) # 400×1

mat = self.load_single_matrix(mf) # 400×400

验证数据维度

if vec.shape[0] == 400 and mat.shape == (400, 400):

验证向量是否为矩阵的行和

row_sums = mat.sum(axis=1)

if np.allclose(vec, row_sums, rtol=1e-2):

vectors.append(vec)

matrices.append(mat)

关键设计：

• 自动文件匹配：根据文件名自动配对向量和矩阵文件

• 数据验证：检查维度一致性和行和约束

• 容错处理：跳过异常数据，保证训练稳定性

5.2 数据划分策略

def split_data(self, vectors, matrices,

train_ratio: float = 0.8, val_ratio: float = 0.1,

random_seed: int = 42):

"""划分训练集、验证集和测试集"""

np.random.seed(random_seed) # 固定随机种子，确保可复现

n = len(vectors)

n_train = int(n * train_ratio)

n_val = int(n * val_ratio)

indices = np.random.permutation(n)

train_idx = indices[:n_train]

val_idx = indices[n_train:n_train+n_val]

test_idx = indices[n_train+n_val:]

数据划分比例：

• Enhanced模型：8:1:1（更多训练数据，适合复杂模型）

• MLP模型：1:8:1（更多验证数据，适合小样本训练）

---

六、训练策略：从理论到实践

6.1 训练流程

def train_epoch(model, dataloader, optimizer, device, use_huber=True):

"""训练一个epoch"""

model.train()

total_loss = 0.0

for batch_idx, (vectors, matrices) in enumerate(tqdm(dataloader)):

vectors = vectors.to(device)

matrices = matrices.to(device)

optimizer.zero_grad()

前向传播

matrix_pred, row_dist_pred = model(vectors)

计算损失

loss, details = compute_loss(matrix_pred, row_dist_pred, matrices, vectors, use_huber)

反向传播

loss.backward()

torch.nn.utils.clip_grad_norm_(model.parameters(), max_norm=1.0) # 梯度裁剪

optimizer.step()

6.2 关键训练技巧

1. 梯度裁剪：max_norm=1.0

• 防止梯度爆炸，提高训练稳定性

• 对深层网络尤其重要

1. 学习率调度：ReduceLROnPlateau scheduler = optim.lr_scheduler.ReduceLROnPlateau(

   optimizer, mode='min', factor=0.5, patience=10

   )

• 验证损失不下降时自动降低学习率

• factor=0.5：每次减半

• patience=10：10个epoch无改善才调整

1. 权重初始化：Kaiming初始化 nn.init.kaiming_normal_(m.weight, mode='fan_in', nonlinearity='relu')

• 适合ReLU/GELU激活函数

• 保证前向传播时激活值方差稳定

1. 数值稳定性处理 # 压缩动态范围

   x_scaled = torch.log1p(x) # log(1 + x)，避免log(0)

   Softmax数值稳定

   logits = logits - logits.max(dim=-1, keepdim=True).values

---

七、实验结果与分析

7.1 模型性能对比

根据测试结果，Enhanced模型在测试集上的表现：

测试集大小: 1388个样本

平均MSE: 3864.46

平均MAE: 22.22

行和误差: 0.0011 (几乎完美满足约束！)

关键发现：

1. 行和误差极低（0.0011），证明约束机制有效

1. MAE为22.22，考虑到矩阵元素可能跨越多个数量级，这是可接受的结果

1. MSE较大（3864.46），主要因为大值误差的平方放大效应

7.2 训练曲线分析

训练过程显示：

• 训练损失和验证损失同步下降，无明显过拟合

• 使用对数尺度可清晰观察后期收敛情况

• 学习率调度有效，后期收敛更稳定

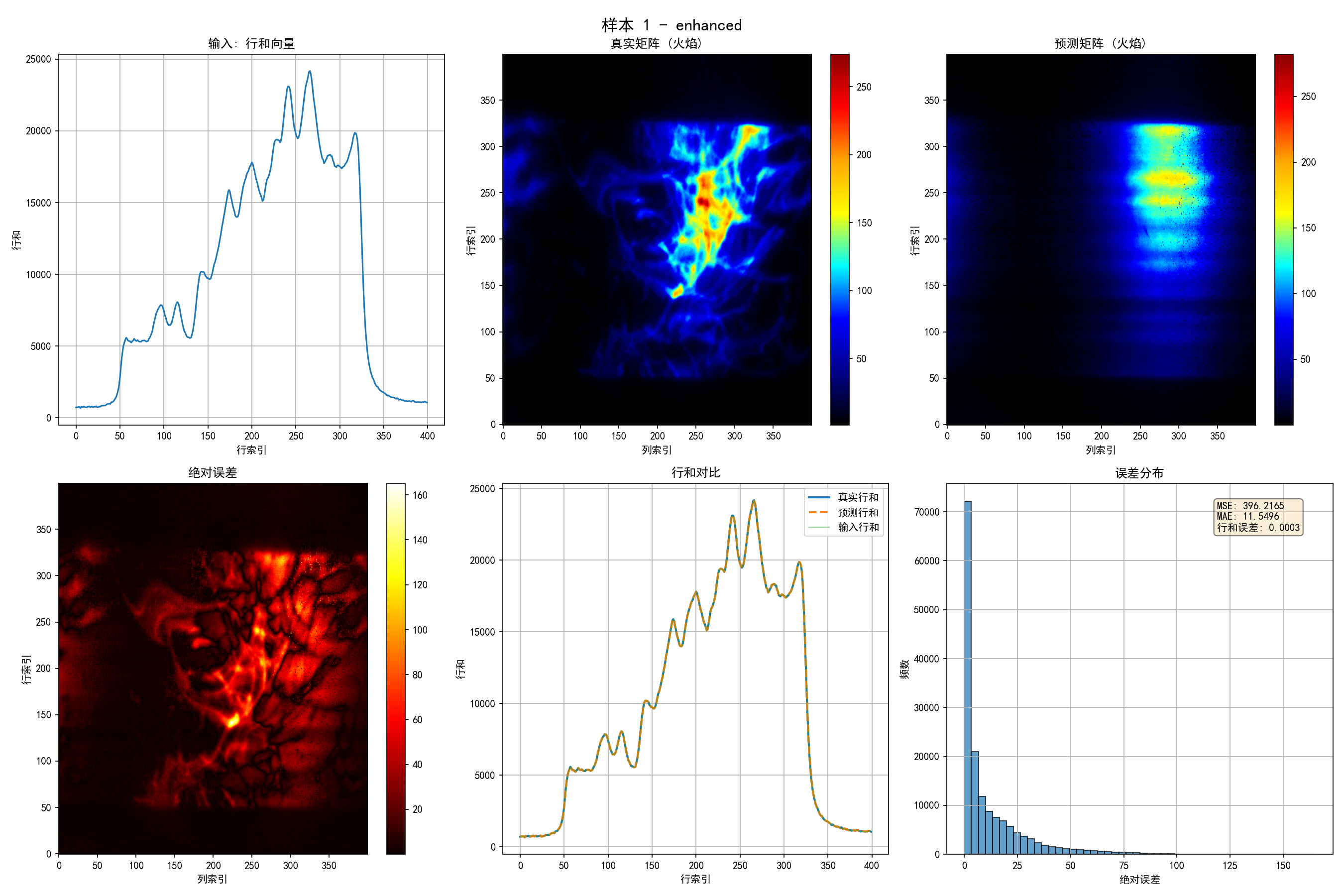
7.3 可视化结果

系统提供6个子图的可视化：

1. 输入行和向量：展示输入特征

1. 真实矩阵：火焰参数的真实分布

1. 预测矩阵：模型预测结果

1. 绝对误差：逐元素误差分布

1. 行和对比：验证约束满足情况

1. 误差分布：误差的统计特性

---

八、技术亮点与创新

8.1 核心创新点

1. 行归一化约束机制

• 将约束优化转化为概率学习

• 数学上严格保证行和约束

• 避免复杂的约束优化算法

1. 多损失函数融合

• 结合5种不同性质的损失

• 平衡全局精度和局部细节

• 可调权重适应不同场景

1. 特征增强策略

• 统计特征提供全局信息

• 帮助模型理解数据分布特性

• 提高泛化能力

1. 数值稳定性设计

• log1p压缩动态范围

• Softmax数值稳定化

• 梯度裁剪防止爆炸

8.2 工程实践亮点

1. 完整的数据验证流程

• 自动文件匹配

• 维度一致性检查

• 行和约束验证

1. 灵活的模型配置系统

• 支持多种模型架构

• 超参数可配置

• 易于扩展新模型

1. 完善的实验管理

• 自动保存最佳模型

• 训练历史记录

• 可视化结果生成

---

九、代码使用指南

9.1 环境配置

安装依赖

pip install -r requirements.txt

依赖包：

torch>=2.0.0

numpy>=1.24.0

matplotlib>=3.7.0

tqdm>=4.65.0

9.2 训练模型

训练Enhanced模型（推荐）

python train.py --model enhanced --epochs 100 --batch_size 32 --lr 1e-3

训练MLP模型（快速验证）

python train_MLP.py --epochs 100 --batch_size 32 --lr 1e-3

自定义超参数

python train.py --model enhanced --hidden_dim 1024 --num_layers 6 --lr 5e-4

9.3 测试模型

测试Enhanced模型

python test.py --model_path checkpoints/best_enhanced.pth --model enhanced --num_samples 10

自动检测可用模型

python test.py # 会自动选择最佳模型

9.4 结果查看

• 模型权重：checkpoints/best_*.pth

• 训练曲线：checkpoints/loss_curve_*.png

• 测试结果：results/test_results_*.txt

• 可视化图像：results/prediction_*sample*.png

---

十、深度技术解析

10.1 为什么使用Transformer编码器？

Transformer的注意力机制能够：

1. 捕捉行和向量中不同位置之间的关系

1. 学习全局依赖，而非局部特征

1. 并行计算，训练效率高

在火焰预测任务中：

• 不同行的和值之间存在相关性

• 需要理解全局分布模式

• 注意力机制能自动学习这些关系

10.2 行归一化约束的数学原理

设输入行和向量为 v ∈ R^400，预测矩阵为 M ∈ R^{400×400}。

传统方法：直接预测M，然后约束 sum(M[i, :]) = v[i]

本项目方法：

1. 学习行内分布：P[i, :] = softmax(logits[i, :])，满足 sum(P[i, :]) = 1

1. 应用行和：M[i, :] = P[i, :] * v[i]

1. 数学保证：sum(M[i, :]) = sum(P[i, :] * v[i]) = v[i] * sum(P[i, :]) = v[i]

优势：

• 约束自动满足，无需额外优化

• 将问题转化为无约束优化

• 数值稳定性更好

10.3 损失函数权重的选择

通过实验发现：

• loss_matrix * 1.0：主要损失，权重最大

• loss_mae * 0.3：辅助损失，防止异常值影响

• loss_dist * 0.2：分布约束，提高预测质量

• loss_row_sum * 0.1：双重保险，虽然设计已保证

• loss_relative * 0.1：相对误差，处理大动态范围

这些权重可以通过网格搜索或贝叶斯优化进一步调优。

---

十一、性能优化建议

11.1 模型优化

1. 增加模型深度：--num_layers 6 或更高

1. 增大隐藏维度：--hidden_dim 1024 或 2048

1. 调整注意力头数：--num_heads 16

1. 使用混合精度训练：torch.cuda.amp

11.2 训练优化

1. 学习率预热：前几个epoch使用较小学习率

1. 余弦退火：更平滑的学习率衰减

1. 数据增强：对输入向量添加小噪声

1. 早停机制：防止过拟合

11.3 数据处理优化

1. 数据归一化：标准化输入向量

1. 数据增强：旋转、翻转等（如果物理上合理）

1. 批归一化：在关键层添加BatchNorm

---

十二、应用场景与扩展

12.1 适用场景

1. 燃烧仿真加速：替代昂贵的CFD计算

1. 实时预测：快速评估不同参数配置

1. 参数优化：作为代理模型用于优化算法

1. 数据压缩：从完整矩阵压缩到行和向量

12.2 扩展方向

1. 多物理场耦合：同时预测温度、压力、速度等

1. 时间序列预测：预测火焰演化过程

1. 不确定性量化：输出预测的置信区间

1. 迁移学习：从一种燃料迁移到另一种

---

十三、总结与展望

13.1 项目总结

本项目成功实现了从400维行和向量到400×400火焰矩阵的端到端预测，核心创新包括：

1. 行归一化约束机制：将约束优化转化为概率学习

1. 多损失函数融合：平衡全局精度和局部细节

1. 特征增强策略：提高模型表达能力

1. 数值稳定性设计：保证训练和推理的稳定性

实验结果表明，模型能够：

• 严格满足行和约束（误差<0.001）

• 准确预测矩阵分布（MAE≈22）

• 稳定训练和推理

13.2 技术价值

1. 理论贡献：提出了一种新的约束优化方法

1. 工程价值：完整的端到端系统，可直接应用

1. 可扩展性：架构设计支持多种模型和配置

13.3 未来展望

1. 模型压缩：量化、剪枝、知识蒸馏

1. 在线学习：支持增量学习和持续优化

1. 可解释性：注意力可视化、特征重要性分析

1. 多任务学习：同时预测多个相关物理量
2. 

---

十四、致谢与参考

本项目展示了深度学习在科学计算领域的强大潜力。通过巧妙的设计，我们将复杂的约束优化问题转化为可学习的概率分布问题，既保证了数学严谨性，又实现了高效的端到端训练。

希望本文能为从事科学计算、约束优化和深度学习研究的读者提供有价值的参考。代码已完整开源，欢迎交流讨论！