【C++】哈希扩展——位图和布隆过滤器的介绍与实现

落羽的落羽2025-12-17 12:47


各位读者大佬好，我是落羽！一个坚持不断学习进步的学生。
如果您觉得我的文章还不错，欢迎多多互三分享交流，一起学习进步！
也欢迎关注我的blog主页: 落羽的落羽

文章目录

  • 一、位图
    • [1. 概念与实现](#1. 概念与实现)
    • [2. std::bitset](#2. std::bitset)
  • 二、布隆过滤器
    • [1. 概念](#1. 概念)
    • [2. 布隆过滤器误判率数学推导](#2. 布隆过滤器误判率数学推导)
    • [3. 实现](#3. 实现)

一、位图

1. 概念与实现

在许多公司的面试题中会考到这样的场景：给40亿个不重复无符号整数，如何快速判断一个数是否在这40亿数中。

如果使用常规思路，每次查询暴力遍历O(N)太慢，排序+二分查找O(NlogN)+O(logN)，内存不足以放下这些数据。

数据是否在给定的整型数据中，结果是在或不在，正好是两种状态，那么可以用一个二进制比特位来代表数据是否存在的信息，比特位为1代表存在，比特位为0代表不在。那么，我们可以设计一个用比特位表示数据是否存在的数据结构------位图！

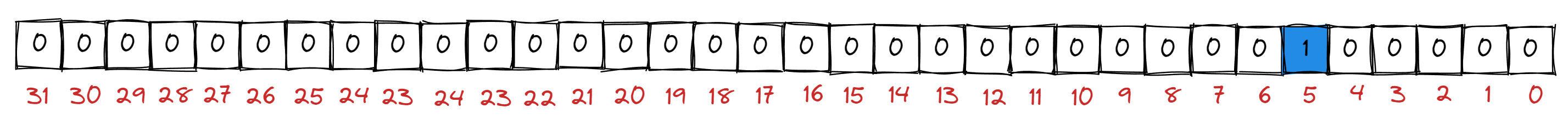
位图本质上是一个直接定址法的哈希表，每个整型值映射到一个比特位，位图提供控制这个比特位的相关接口，最主要的是set、reset、test：

cpp 复制代码 
namespace lydly
{
	template<size_t N> // 模版参数表示有多少个数据
	class bitset
	{
	public:
		bitset()
		{
			// 一个int有32位，+1为了向上取整，初始全用0填充
			_bits.resize(N / 32 + 1, 0);
		}

		void set(size_t x) // 将一个数的映射位设为1
		{
			// i找这个数在第几个int
			// j找这个数在这个int中的第几个位
			// 利用或运算将这一位设为1，不改变其他位
			size_t i = x / 32;
			size_t j = x % 32;
			_bits[i] |= (1 << j);
		}

		void reset(size_t x) // 将一个数的映射位设为0
		{
			// i找这个数在第几个int
			// j找这个数在这个int中的第几个位
			// 利用且运算将这一位设为0，不改变其他位
			size_t i = x / 32;
			size_t j = x % 32;
			_bits[i] &= ~(1 << j);
		}

		bool test(size_t x) // 如果x映射1返回true，映射0返回false
		{
			size_t i = x / 32;
			size_t j = x % 32;
			return _bits[i] & (1 << j);
		}

	private:
		vector<int> _bits; // 位图与数组中是什么类型无关，我们使用它的位
	};
}

简单测试一下：

开232个比特位不在话下

cpp 复制代码 
#include"bitset.h"

int main()
{
	lydly::bitset<0xffffffff> bs; // 开2^32位

	for (size_t i = 0; i < 5000; i++)
	{
		bs.set(i);
	}
	for (int i = 0; i < 100; i++)
	{
		int n = rand() % 10000;
		if (bs.test(n))
		{
			cout << n << "存在" << endl;
		}
		else
		{
			cout << n << "不存在" << endl;
		}
	}
	return 0;
}

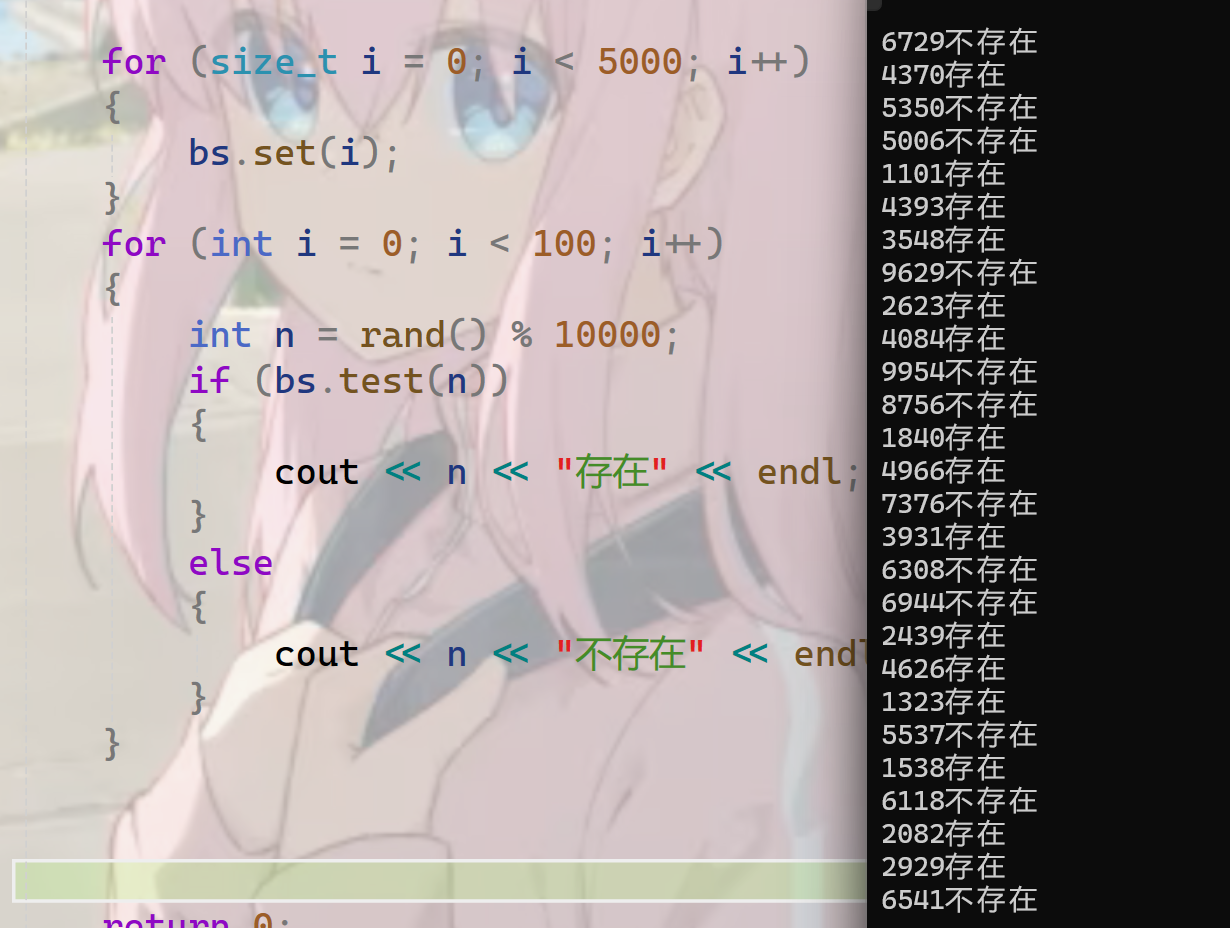
有了位图这样的数据结构，解决上面的问题就很轻松了。40亿个无符号整数，数的范围是0~232，所以要给位图开232个位。然后从文件中依次读取每个数存放到位图中，之后的每次查询，就可以达到O(1)的速度了。

2. std::bitset

实际上，C++库中已经提供了位图bitset，核心接口还是set、reset、test等。还有一些其他功能，如operator[]允许我们像数组一样用下标控制位，to_string可以将位图转化为一个01字符串。


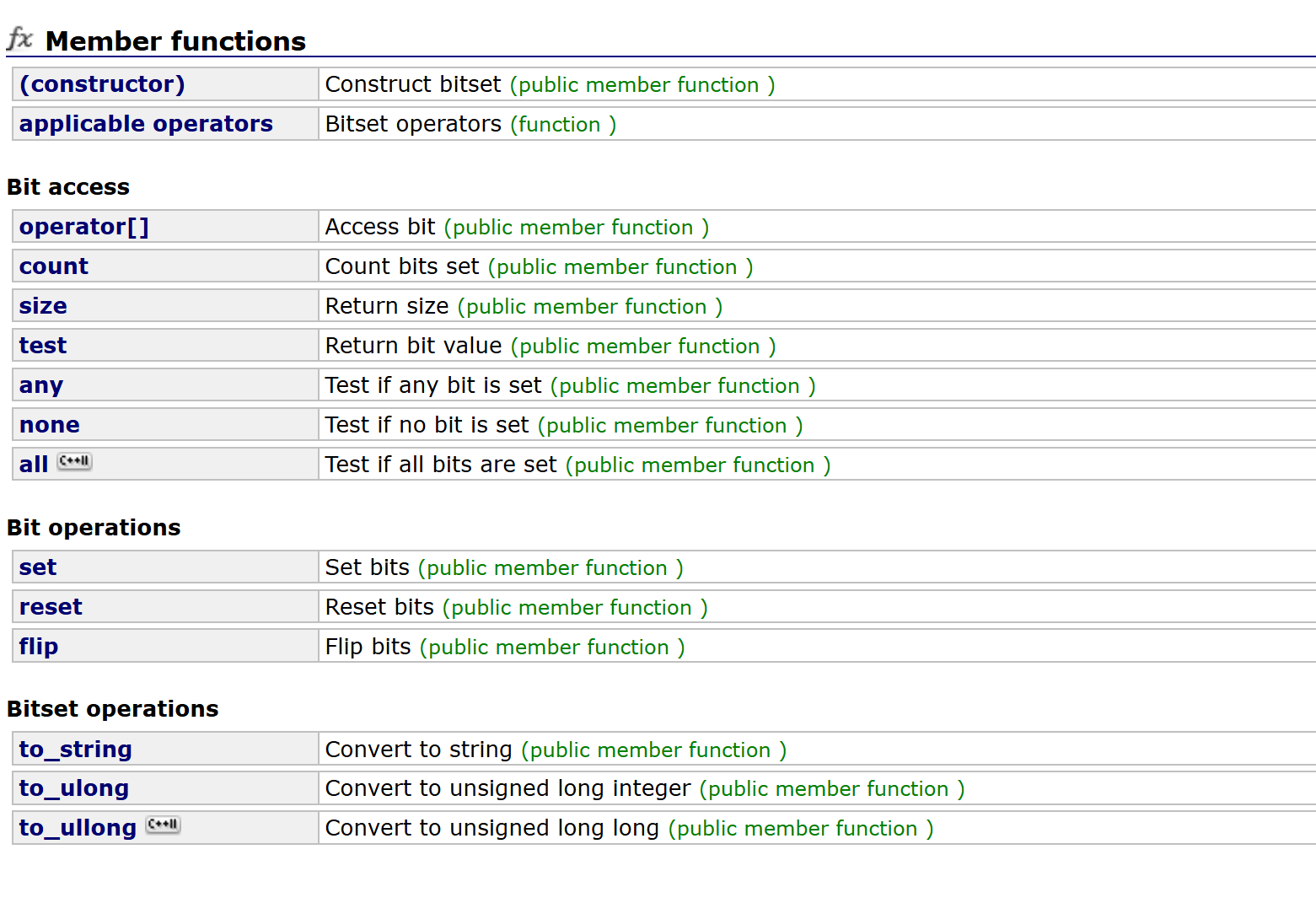
位图的优点是增删查改的效率很高，节省空间。缺点是他只适用于整型数据。

二、布隆过滤器

1. 概念

在一些场景下，有海量数据需要查询判断是否存在，但这些数据不是整型，那么就无法使用位图了，红黑树、哈希表这些内存空间不足。这种场景下就可以使用布隆过滤器。

布隆过滤器是由布隆提出的一种概率型数据结构，特点是可以高效插入和查询，很难进行删除，它可以查询某个数据"可能在"或"一定不在"，其思路是利用哈希函数将一个非整型数据映射为整型，再映射到比特位中 。这种方式不仅可以提升查询效率，也能节省大量内存。

但是，只用一个哈希函数映射到一个位时，很容易造成哈希冲突，为了降低哈希冲突，一般会通过使用多个哈希函数，映射到多个位上，共同表示数据是否存在，这些位都为1才表示这个数据存在 。布隆过滤器和哈希桶不一样，它始终无法解决哈希冲突，只能尽可能降低冲突率。因此，用布隆过滤器判断一个数据是否存在，不是完全准确的！判断一个数据不存在，是准确的！

2. 布隆过滤器误判率数学推导

布隆过滤器的数学推导过程比较复杂：

假设变量：

  • m m m：布隆过滤器的bit长度
  • n n n：插入布隆过滤器的元素个数
  • k k k：哈希函数的个数

概率推导：

  1. 布隆过滤器哈希函数条件下某个位设置为1的概率： 1 m \frac{1}{m} m1

  2. 布隆过滤器哈希函数条件下某个位设置不为1的概率： 1 − 1 m 1 - \frac{1}{m} 1−m1

  3. 经过 k k k次哈希后，某个位置依旧不为1的概率： ( 1 − 1 m ) k (1 - \frac{1}{m})^k (1−m1)k

    根据极限公式： lim ⁡ n → ∞ ( 1 − 1 m ) − m = e \lim_{n \to \infty}(1 - \frac{1}{m})^{-m} = e limn→∞(1−m1)−m=e

    推导出：
    ( 1 − 1 m ) k = ( ( 1 − 1 m ) m ) k m ≈ e − k m (1 - \frac{1}{m})^k = ((1 - \frac{1}{m})^m)^\frac{k}{m} \approx e^{-\frac{k}{m}} (1−m1)k=((1−m1)m)mk≈e−mk

  4. 添加 n n n个元素某个位置不置为1的概率： ( 1 − 1 m ) k n ≈ e − k n m (1 - \frac{1}{m})^{kn} \approx e^{-\frac{kn}{m}} (1−m1)kn≈e−mkn

  5. 添加 n n n个元素某个位置置为1的概率： 1 − ( 1 − 1 m ) k n ≈ 1 − e − k n m 1 - (1 - \frac{1}{m})^{kn} \approx 1 - e^{-\frac{kn}{m}} 1−(1−m1)kn≈1−e−mkn

  6. 查询一个元素， k k k次hash后误判的概率（都命中1的概率）： ( 1 − ( 1 − 1 m ) k n ) k ≈ ( 1 − e − k n m ) k (1 - (1 - \frac{1}{m})^{kn})^k \approx (1 - e^{-\frac{kn}{m}})^k (1−(1−m1)kn)k≈(1−e−mkn)k

结论：

  • 布隆过滤器的误判率为：
    f ( k ) = ( 1 − e − k n m ) k f(k) = (1 - e^{-\frac{kn}{m}})^k f(k)=(1−e−mkn)k
    也可表示为：
    f ( k ) = ( 1 − 1 e k n m ) k f(k) = (1 - \frac{1}{e^\frac{kn}{m}})^k f(k)=(1−emkn1)k

  • 误判率变化规律：在 k k k一定的情况下， n n n增加时误判率增加， m m m增加时误判率减少。

  • 最优哈希函数个数：在 m m m和 n n n一定时，对误判率公式求导，可得 k = m n ln ⁡ 2 k = \frac{m}{n} \ln2 k=nmln2时误判率最低。

  • 期望的误判率 p p p和插入数据个数 n n n确定时，再把上面的公式带入误判率公式可得到布隆过滤器bit长度：
    m = − n ∗ ln ⁡ p ( ln ⁡ 2 ) 2 m = -\frac{n * \ln p}{(\ln2)^2} m=−(ln2)2n∗lnp

3. 实现

我们要给布隆过滤器多个哈希函数算法，可以借鉴前人创造的一些算法：

cpp 复制代码 
struct HashFuncBKDR
{
	/* 本算法由于在Brian Kernighan与Dennis Ritchie的《The CProgramming Language》
	一书被展示而得名，是一种简单快捷的hash算法，也是Java目前采用的字符串的Hash算法，累乘因子为31*/
	size_t operator()(const std::string& s)
	{
		size_t hash = 0;
		for (auto ch : s)
		{
			hash *= 31;
			hash += ch;
		}
		return hash;
	}
};

struct HashFuncAP
{
	// 由Arash Partow发明的一种hash算法。  
	size_t operator()(const std::string& s)
	{
		size_t hash = 0;
		for (size_t i = 0; i < s.size(); i++)
		{
			if ((i & 1) == 0) 
			{
				hash ^= ((hash << 7) ^ (s[i]) ^ (hash >> 3));
			}
			else 
			{
				hash ^= (~((hash << 11) ^ (s[i]) ^ (hash >> 5)));
			}
		}

		return hash;
	}
};

struct HashFuncDJB
{
	// 由Daniel J. Bernstein教授发明的一种hash算法。 
	size_t operator()(const std::string& s)
	{
		size_t hash = 5381;
		for (auto ch : s)
		{
			hash = hash * 33 ^ ch;
		}

		return hash;
	}
};

布隆过滤器的实现：

cpp 复制代码 
#include"bitset.h"
#include<string>

struct HashFuncBKDR
{
	/* 本算法由于在Brian Kernighan与Dennis Ritchie的《The CProgramming Language》
	一书被展示而得名，是一种简单快捷的hash算法，也是Java目前采用的字符串的Hash算法，累乘因子为31*/
	size_t operator()(const std::string& s)
	{
		size_t hash = 0;
		for (auto ch : s)
		{
			hash *= 31;
			hash += ch;
		}
		return hash;
	}
};

struct HashFuncAP
{
	// 由Arash Partow发明的一种hash算法。  
	size_t operator()(const std::string& s)
	{
		size_t hash = 0;
		for (size_t i = 0; i < s.size(); i++)
		{
			if ((i & 1) == 0) 
			{
				hash ^= ((hash << 7) ^ (s[i]) ^ (hash >> 3));
			}
			else 
			{
				hash ^= (~((hash << 11) ^ (s[i]) ^ (hash >> 5)));
			}
		}

		return hash;
	}
};

struct HashFuncDJB
{
	// 由Daniel J. Bernstein教授发明的一种hash算法。 
	size_t operator()(const std::string& s)
	{
		size_t hash = 5381;
		for (auto ch : s)
		{
			hash = hash * 33 ^ ch;
		}

		return hash;
	}
};


template<size_t N, // 数据个数
	size_t X = 5,  // 每个数据占用的平均bit位数（默认5） 
	class K = std::string, // 数据类型，默认设为string
	class Hash1 = HashFuncBKDR, // 哈希函数个数k = m/n*ln2时误判率最低，这里计算约为3，所以给出三个不同的哈希函数
	class Hash2 = HashFuncAP,
	class Hash3 = HashFuncDJB>
class BloomFilter
{
public:

	// 将一个数据映射的每个位设为1
	void set(const K& key)
	{
		size_t hash1 = Hash1()(key) % M;
		size_t hash2 = Hash2()(key) % M;
		size_t hash3 = Hash3()(key) % M;

		_bs.set(hash1);
		_bs.set(hash2);
		_bs.set(hash3);
	}

	// 判断一个数据是否存在，要判断映射的每一位是否都为1
	// 返回true不一定准确，因为这一位1可能是别人的1
	// 返回false一定准确，因为这一位是0，数据一定不存在
	bool test(const K& key)
	{
		size_t hash1 = Hash1()(key) % M;
		if (!_bs.test(hash1))
		{
			return false;
		}

		size_t hash2 = Hash2()(key) % M;
		if (!_bs.test(hash2))
		{
			return false;
		}

		size_t hash3 = Hash3()(key) % M;
		if (!_bs.test(hash3))
		{
			return false;
		}

		return true; // 可能存在误判
	}

private:
	static const size_t M = N * X;
	lydly::bitset<M> _bs;
};

简单测试一下：

cpp 复制代码 
#include"BloomFilter.h"
int main()
{
	BloomFilter<100> bf;
	
	// 生成"test1"、"test2"、..."test99"字符串，插入bf中
	for (int i = 0; i < 100; i++)
	{
		std::string s("test");
		s += std::to_string(i);
		bf.set(s);
	}

	// 测试判断确定存在的数据
	for (int i = 0; i < 100; i++)
	{
		std::string s("test");
		s += std::to_string(i);
		if (bf.test(s))
		{
			cout << s << "存在" << endl;
		}
		else
		{
			cout << s << "不存在" << endl;
		}
	}

	// 测试判断不存在的数据，生成"test1000"、...、"test1500"字符串
	for (int i = 1000; i < 1500; i++)
	{
		std::string s("test");
		s += std::to_string(i);
		if (bf.test(s))
		{
			cout << s << "存在" << endl;
		}
		else
		{
			cout << s << "不存在" << endl;
		}
	}


	return 0;
}

第一段测试没问题，这些字符串都是存在的：

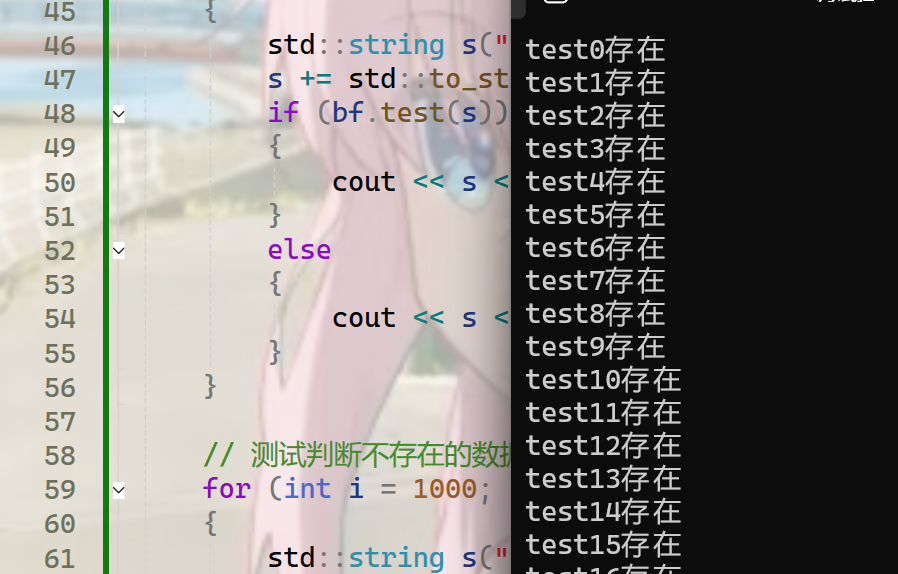
而到了后面，就发现出现了误判，个别字符串不存在，但是判断成了存在：

布隆过滤器的优点是，效率高，节省空间，相比于位图可以适用于记录各种类型的数据。
缺点很明显，存在误判的情况，不是完全准确的。而且布隆过滤器不好支持删除，删除一个数据，不能直接将它的所有位设为0，因为可能还有别的数据映射到了这个位，具体分析十分复杂。

本篇完，感谢阅读！

我的博客即将同步至腾讯云开发者社区，邀请大家一同入驻：https://cloud.tencent.com/developer/support-plan?invite_code=gpaa1e1wuni

相关推荐
2301_8008951016 小时前
hh的蓝桥杯每日一题
算法·职场和发展·蓝桥杯
老鱼说AI16 小时前
现代计算机系统1.2：程序的生命周期从 C/C++ 到 Rust
c语言·c++·算法
rayufo16 小时前
深度学习对三维图形点云数据分类
人工智能·深度学习·分类
仰泳的熊猫16 小时前
题目1099:校门外的树
数据结构·c++·算法·蓝桥杯
求梦82016 小时前
【力扣hot100题】反转链表（18）
算法·leetcode·职场和发展
智航GIS16 小时前
10.7 pyspider 库入门
开发语言·前端·python
NAGNIP16 小时前
机器学习特征工程中的特征选择
算法·面试
ayaya_mana16 小时前
VS Code 远程开发：SSH连接与远程资源管理器的配置
linux·ide·windows·vscode·远程资源管理
跟着珅聪学java16 小时前
JavaScript 底层原理
java·开发语言
l1t16 小时前
DeepSeek辅助编写的利用位掩码填充唯一候选数方法求解数独SQL
数据库·sql·算法·postgresql
热门推荐
01GitHub 镜像站点02Labelme从安装到标注：零基础完整指南03Linux下V2Ray安装配置指南04安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）05jdk21下载、安装（Windows、Linux、macOS）06KGG转MP3工具|非KGM文件|解密音频07Claude Code 2.1.2 升级报错？别折腾了，一行命令搞定08【踩坑笔记】50系显卡适配的 PyTorch 安装092025-04-03 Latex学习1——本地配置Latex + VScode环境10UV安装并设置国内源