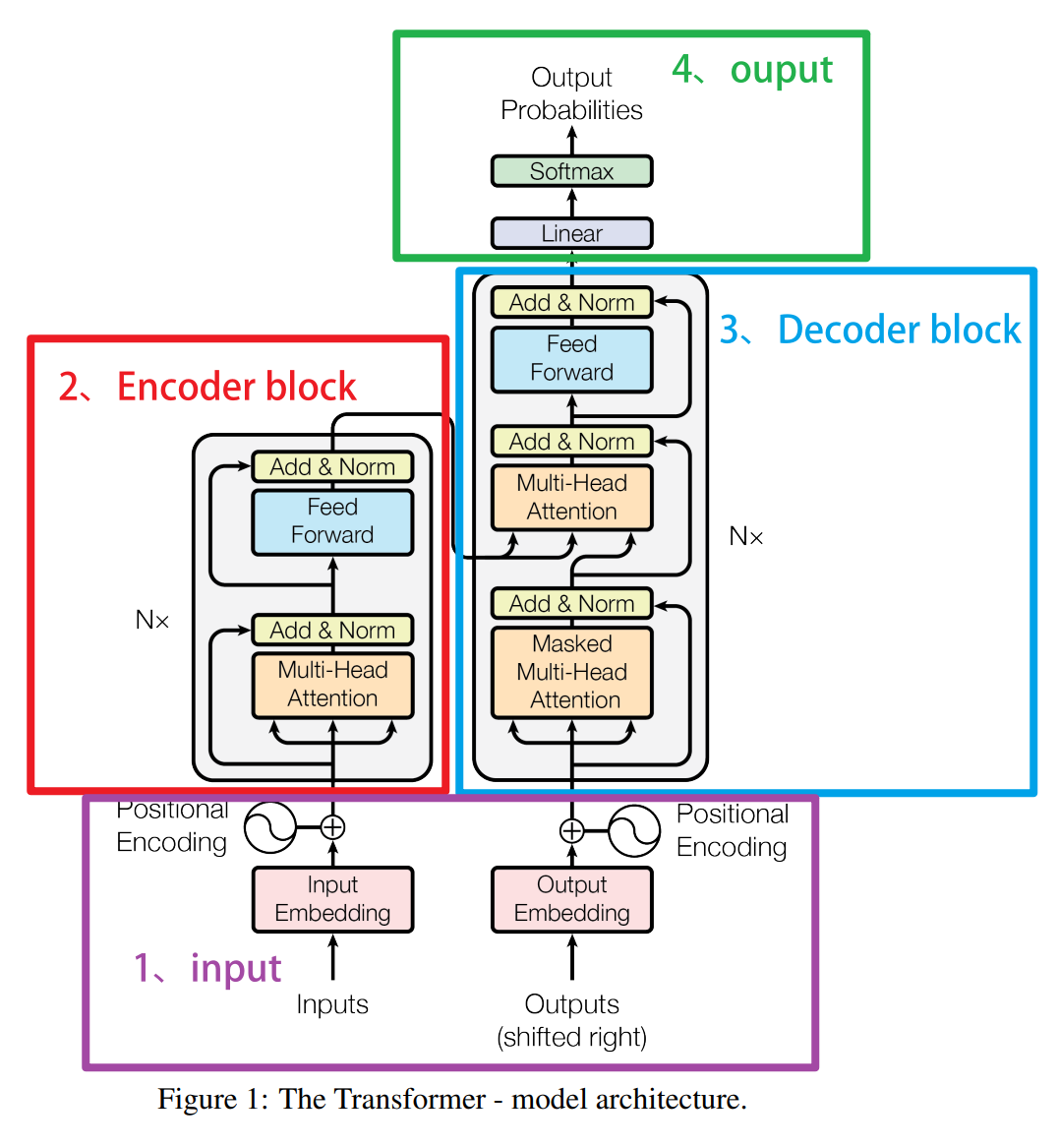
在transformer中,embedding层位于encoder和decoder之前,主要负责进行语义编码。Embedding层将离散的词汇或符号转换为连续的高维向量,使得模型能够处理和学习这些向量的语义关系。通过嵌入表示,输入的序列可以更好地捕捉到词与词之间的相似性和关系。此外,在输入到编码器和解码器之前,通常还会添加位置编码(Positional Encoding),因为transformer没有内置的序列顺序信息,也就是说 Attention 机制本身会带来位置信息的丧失。
一、位置编码概述
- 位置信息为什么重要?它可以从哪里来?
首先,位置信息就是顺序的信息,字符排列的顺序会影响语句的理解(还记得"屡战屡败"和"屡败屡战"的例子吗?同样的词在句子不同的地方出现,也可能会有不同的含义),我们说transformer丧失了位置信息,意思是transformer并不理解样本与样本之间是按照什么顺序排列的(也就是不知道样本在序列中具体的位置)。
还记得RNN和LSTM是如何处理数据的吗?RNN和LSTM以序列的方式处理输入数据,即一个时间步一个时间步地处理输入序列的每个元素。每个时间步的隐藏状态依赖于前一个时间步的隐藏状态。这种机制天然地捕捉了序列的顺序信息。由于RNN和LSTM在处理序列时会保留前一时间步的信息并传递到下一时间步,所以它们能够内在地理解和处理序列的时间依赖关系和顺序信息。然而,与RNN和LSTM不同,transformer并不以序列的方式逐步处理输入数据,而是一次性处理整个序列。Attention 能够通过点积的方式一次性计算出所有向量之间的相关性、并且多头注意力机制中不同的头还可以并行,因此 Attention 与 transformer 缺乏天然的顺序信息。
- 相关性计算过程中有标识,这些标识不能够成为位置信息吗?什么信息才算是位置信息/顺序信息呢?
由上节文章 注意力机制的原理 可知,在注意力机制中,权重矩阵 s o f t m a x ( Q K T d k ) softmax(\frac{QK^{T}}{\sqrt{d_k}}) softmax(dk QKT) 中的每个元素 a i j a_{ij} aij 表示序列中位置 i i i 和位置 j j j 之间的相关性,但是却并没有假设这两个相关的元素之间的位置信息。具体来说,虽然我们使用了1、2这样的脚标,但 Attention 实际在进行计算的时候,只会认知两个具体的相关性数字,并没有显性地认知到脚标。
Z ( A t t e n t i o n ) = ( a 11 a 12 a 21 a 22 ) ( v 11 v 12 v 13 v 21 v 22 v 23 ) = ( ( a 11 v 11 + a 12 v 21 ) ( a 11 v 12 + a 12 v 22 ) ( a 11 v 13 + a 12 v 23 ) ( a 21 v 11 + a 22 v 21 ) ( a 21 v 12 + a 22 v 22 ) ( a 21 v 13 + a 22 v 23 ) ) \mathbf{Z(Attention)} = \begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix} \begin{pmatrix} v_{11} & v_{12} & v_{13} \\ v_{21} & v_{22} & v_{23} \end{pmatrix} = \begin{pmatrix} (a_{11}v_{11} + a_{12}v_{21}) & (a_{11}v_{12} + a_{12}v_{22}) & (a_{11}v_{13} + a_{12}v_{23}) \\ (a_{21}v_{11} + a_{22}v_{21}) & (a_{21}v_{12} + a_{22}v_{22}) & (a_{21}v_{13} + a_{22}v_{23}) \end{pmatrix} Z(Attention)=(a11a21a12a22)(v11v21v12v22v13v23)=((a11v11+a12v21)(a21v11+a22v21)(a11v12+a12v22)(a21v12+a22v22)(a11v13+a12v23)(a21v13+a22v23))
由于transformer模型放弃了"逐行对数据进行处理"的方式,而是一次性处理一整张表单,因此它不能直接像循环神经网络RNN那样在训练过程中就捕捉到单词与单词之间的位置信息。在经典的深度学习场景当中,最典型的顺序信息就是数字的大小 。由于数字天生是带有大小顺序的,因此数字本身可以被认为是含有顺序一个信息,只要让有顺序的信息和有顺序的数字相匹配,就可以让算法天然地认知到相应的顺序。因此我们自然而然地想要对样本的位置本身进行"编码" ,利用数字本身自带的顺序来告知transformer。
- 位置信息如何被告知给
Attention/transformer这样的算法?
为了解决位置信息的问题,transformer引入了位置编码(positional encoding)技术来补充语义词嵌入。我们首先将样本的位置转变成相应的数字或向量,然后让位置编码的这个向量被加到原有的词嵌入向量 embedding 向量上,这样模型就可以同时知道一个词的语义和它在句子中的位置。
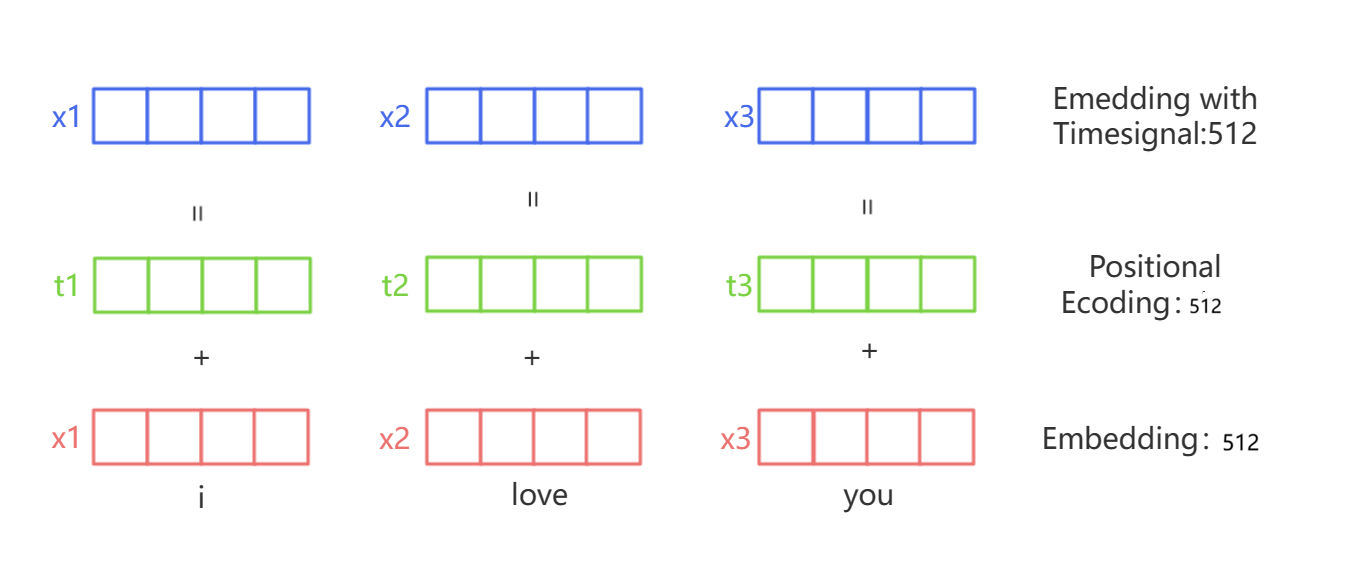
位置编码使用了一种特殊的函数,这个函数会为序列中的每个位置生成一个向量。对于一个特定的位置,这个函数生成的向量在所有维度上的值都是不同的。这保证了每个位置的编码都是唯一的,而且不同位置的编码能够保持一定的相对关系。在transformer的位置编码中,我们需要对每个词的每个特征值给与位置编码,所有这些特征位置的编码共同组合成了一个样本的位置编码 。例如,当一个样本拥有4个特征时,我们的位置编码也会是包含4个数字的一个向量,而不是一个单独的编码。因此,位置编码矩阵是一个与 embedding 后的矩阵结构相同的矩阵。
在transformer模型中,词嵌入和位置编码被相加,然后输入到模型的第一层。这样,transformer就可以同时处理词语的语义和它在句子中的位置信息。这也是transformer模型在处理序列数据,特别是自然语言处理任务中表现出色的一个重要原因。
二、正余弦位置编码
2.1 正余弦位置编码介绍
在过去最为经典的位置编码就是 OrdinalEncoder 顺序编码,但在transformer中我们需要的是一个编码向量,而非单一的编码数字,因此 OrdinalEncoder 编码就不能使用了。在众多的、构成编码向量的方式中,transformer选择了"正余弦编码"这一特别的方式。让我们一起来看看正余弦编码的含义。
首先,正余弦编码是使用正弦函数和余弦函数来生成具体编码值的编码方式。对于任意的词向量(也就是数据中的一个样本),正余弦编码在偶数维度上采用了 sin 函数来编码,奇数维度采用了 cos 函数来编码,sin 函数与 cos 函数交替使用,最终构成一个多维度的向量------
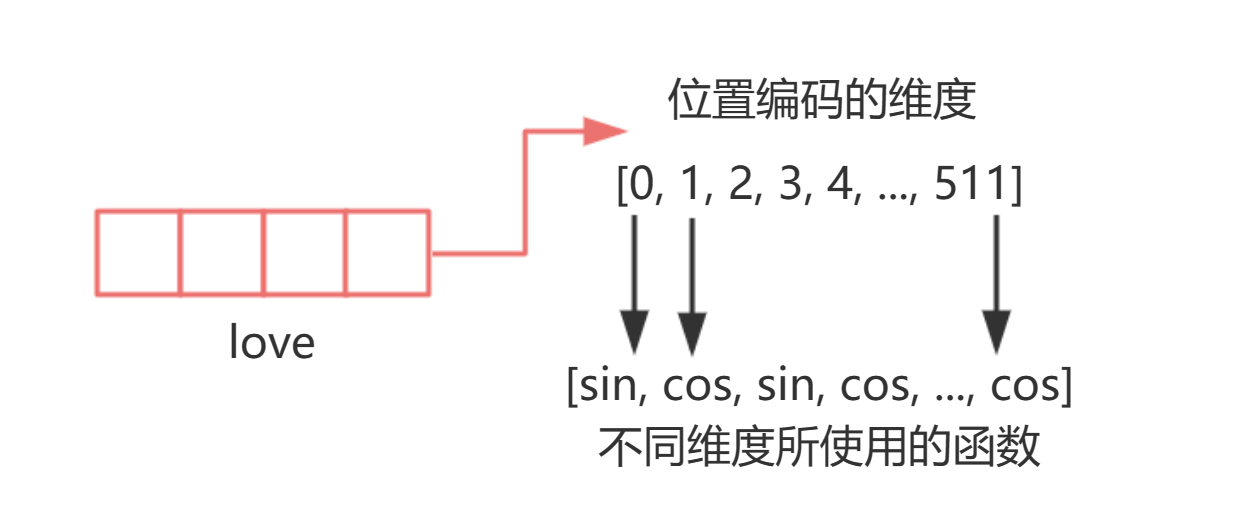
通过对不同的维度进行不同的三角函数编码,来构成一串独一无二的编码组合。这种编码组合与 embedding 类似,都是将信息投射到一个高维空间当中,只不过正余弦编码是将样本的位置信息(也就是样本的索引)投射到高维空间中,且每一个特征的维度代表了这个高维空间中的一维度。对正余弦编码来说,编码数字本身是依赖于样本的位置信息(索引)、所有维度的编号、以及总维度数三个因子计算出来的。
具体来看,正余弦编码的公式如下:
-
正弦位置编码(
Sinusoidal Positional Encoding)
P E ( p o s , 2 i ) = sin ( p o s 1000 0 2 i d model ) PE_{(pos, 2i)} = \sin \left( \frac{pos}{10000^{\frac{2i}{d_{\text{model}}}}} \right) PE(pos,2i)=sin(10000dmodel2ipos) -
余弦位置编码(
Cosine Positional Encoding)
P E ( p o s , 2 i + 1 ) = cos ( p o s 1000 0 2 i d model ) PE_{(pos, 2i+1)} = \cos \left( \frac{pos}{10000^{\frac{2i}{d_{\text{model}}}}} \right) PE(pos,2i+1)=cos(10000dmodel2ipos)
其中------
pos代表样本在序列中的位置,也就是样本的索引(是三维度中的seq_len/vocal_size/time_step这个维度上的索引)- 2 i 2i 2i和 2 i + 1 2i+1 2i+1分别代表
embedding矩阵中的偶数和奇数维度索引,当我们让i从0开始循环增长时,可以获得[0,1,2,3,4,5,6...]这样的序列。 - d model d_{\text{model}} dmodel 代表
embedding后矩阵的总维度。
在这里,你可以选择停下脚步、开启下一节课程,你也可以选择继续听更深入的关于位置编码的内容。这里有选择的原因是,位置编码作为深度学习和时间序列处理过程中非常重要的一种技术,在不同的场景下被频繁地使用,我们可以将其用于纹理建模、声音处理、信号处理、震动分析等多种场合,但同时,我们也将它作为一种行业惯例在进行使用,因此你或许无需对正余弦位置编码进行特别深入的探索。
但正余弦位置编码本身是一种非常奇妙的结构,在接下来的内容中,我将带你仔细剖析正余弦位置编码的诸多细节和意义。
2.2 正余弦位置编码意义
为什么要使用正余弦编码?它有什么意义?
-
正弦位置编码(
Sinusoidal Positional Encoding)
P E ( p o s , 2 i ) = sin ( p o s 1000 0 2 i d model ) PE_{(pos, 2i)} = \sin \left( \frac{pos}{10000^{\frac{2i}{d_{\text{model}}}}} \right) PE(pos,2i)=sin(10000dmodel2ipos) -
余弦位置编码(
Cosine Positional Encoding)
P E ( p o s , 2 i + 1 ) = cos ( p o s 1000 0 2 i d model ) PE_{(pos, 2i+1)} = \cos \left( \frac{pos}{10000^{\frac{2i}{d_{\text{model}}}}} \right) PE(pos,2i+1)=cos(10000dmodel2ipos)
首先我们先来看pos,pos是样本的索引,它有多大会取决于实际的数据尺寸。如果一个时间序列或文本数据是很长的序列,那pos数值本身也会变得很大。假设我们使用很大的数值与原本的 embedding 序列相加,那位置编码带来的影响可能会远远超过原始的语义、会导致喧宾夺主的问题,因此我们天然就有限制位置编码的大小的需求。在这个角度来看,使用sin和cos这样值域很窄的函数、就能够很好地限制位置编码地大小。
正余弦编码的意义①:sin和cos函数值域有限,可以很好地限制位置编码的数字大小。
假设我们使用的是单变量序列,那我们或许只需要 sin(pos) 或者 cos(pos) 看起来就足够了,但为了给每个不同的维度都进行编码,我们肯定还要做点儿别的文章 。首先,位置信息和语义信息一样,当我们将其投射到高维空间时,我们也在尝试用不同的维度来解读位置信息。但我们使用正弦余弦这样的三角函数时,如何能够将信息投射到不同的维度呢------答案是创造各不相同的 sin 和 cos 函数。虽然都是正弦/余弦函数,但我们可以为函数设置不同的频率来获得各种高矮胖瘦的函数------
python
import numpy as np
import matplotlib.pyplot as plt
# 定义绘制正弦函数的函数
def plot_sin_functions(num_functions):
y = np.linspace(0, 10, 1000) # 定义 y 轴范围
colors = plt.cm.viridis(np.linspace(0, 1, num_functions)) # 生成颜色序列
fig, ays = plt.subplots(3, 3, figsize=(12, 9)) # 创建3y3子图
# 绘制每个正弦函数
for i, ay in enumerate(ays.flat):
if i < num_functions:
frequency = (i + 1) * 0.5 # 通过增加倍数来调整频率
y = np.sin(frequency * y)
ay.plot(y, y, label=f'Function {i+1}', color=colors[i])
ay.set_title(f'Function {i+1}')
ay.set_ylabel('y')
ay.set_ylabel('sin(y)')
ay.legend()
plt.tight_layout()
plt.show()
# 绘制9个正弦函数
plot_sin_functions(9)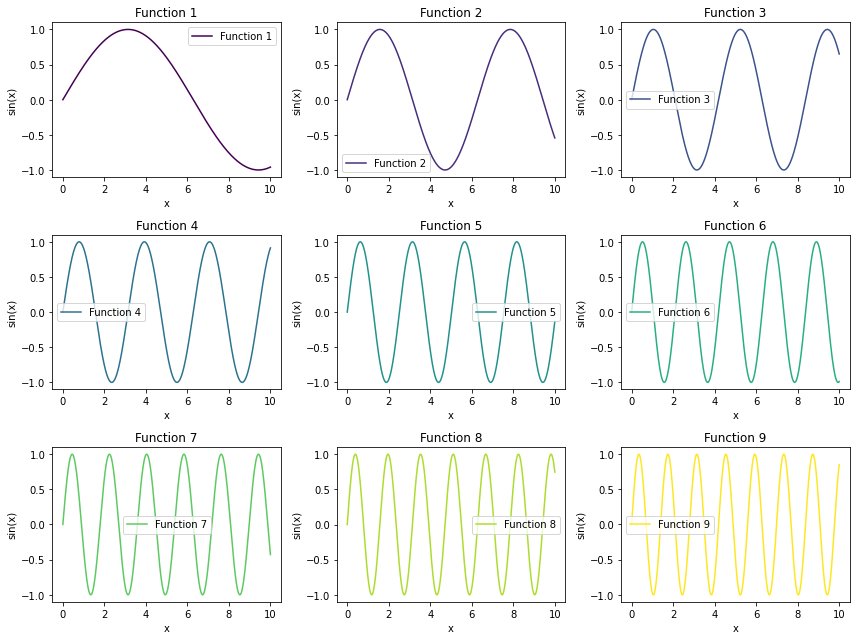
如果能够将不同的特征投射到不同频率的sin和cos函数上,就可以让每个特征都投射到一个独特的维度上,各类不同的信息维度共同构成一个解构位置信息的空间,就能够形成对位置信息的深度解读。
正余弦编码的意义②:通过调节频率,我们可以得到多种多样的sin和cos函数,从而可以将位置信息投射到每个维度都各具特色、各不相同的高维空间,以形成对位置信息的更好的表示。
-
正弦位置编码(
Sinusoidal Positional Encoding)
P E ( p o s , 2 i ) = sin ( p o s 1000 0 2 i d model ) PE_{(pos, 2i)} = \sin \left( \frac{pos}{10000^{\frac{2i}{d_{\text{model}}}}} \right) PE(pos,2i)=sin(10000dmodel2ipos) -
余弦位置编码(
Cosine Positional Encoding)
P E ( p o s , 2 i + 1 ) = cos ( p o s 1000 0 2 i d model ) PE_{(pos, 2i+1)} = \cos \left( \frac{pos}{10000^{\frac{2i}{d_{\text{model}}}}} \right) PE(pos,2i+1)=cos(10000dmodel2ipos)
接下来的问题就是如何赋予sin和cos函数不同的频率了------在sin和cos函数的自变量上乘以不同的值,就可以获得不同频率的sin和cos函数。
y = s i n ( f r e q u e n c y ∗ y ) y = sin(frequency * y) y=sin(frequency∗y)
在位置编码的场景下,我们的自变量是样本的位置pos,因此特征的位置(2i 和 2i+1 )就可以被用来创造不同的频率。在这里,我们对pos这个数字进行了scaling(压缩)的行为。具体地说,我们使用了 1000 0 2 i d model 10000^{\frac{2i}{d_{\text{model}}}} 10000dmodel2i来作为我们缩放的因子,将它作为除数放在pos的下方。但这其实是在pos的基础上乘以 1 1000 0 2 i d model \frac{1}{10000^{\frac{2i}{d_{\text{model}}}}} 10000dmodel2i1这个频率的行为。因此,引入特征位置本身来进行缩放可以带来不同的频率,帮助我们将位置信息pos投射不同频率的三角函数上,确保不同位置(pos)在不同的特征维度(2i 和 2i+1 )上有不同的编码值。
那下一个问题是,这些正余弦函数的频率是随机的吗?我们应该如何控制它呢?正余弦编码最为巧妙的地方来了------通过让位置信息pos乘以 1 1000 0 2 i d model \frac{1}{10000^{\frac{2i}{d_{\text{model}}}}} 10000dmodel2i1这个频率,特征编号比较小的特征会得到大频率,会被投射到高频率的正弦函数上,而特征编号较大的特征会得到小频率,会被投射到低频率的正弦函数上。👇
python
import numpy as np
import matplotlib.pyplot as plt
# 设置参数
d_model = 512
i = np.arange(0, 512) # 维度索引从0到20
# 绘制图像
plt.figure(figsize=(14, 8))
for pos in pos_values:
values = 1 / (10000 ** (2 * i / d_model))
plt.plot(i, values, label=f'pos={pos}')
plt.title('i vs 1 / (10000^(2i/d_model))')
plt.ylabel('feature_indey')
plt.ylabel('1 / (10000^(2i/d_model))')
plt.legend()
plt.grid(True)
plt.show()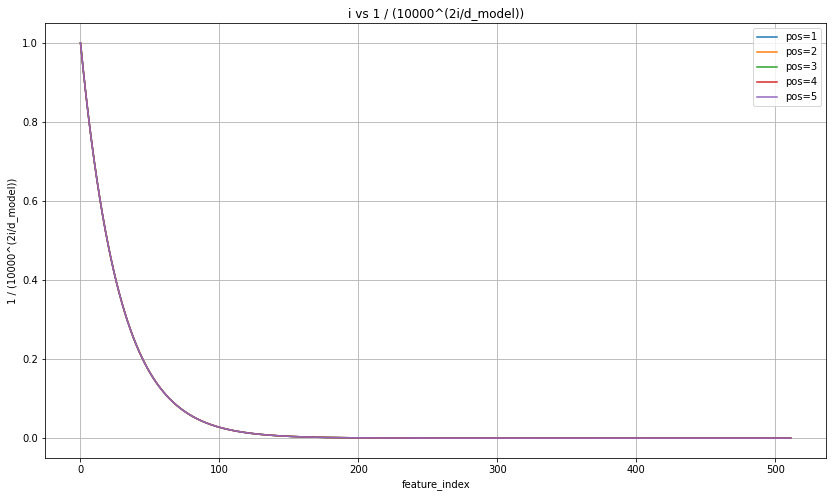
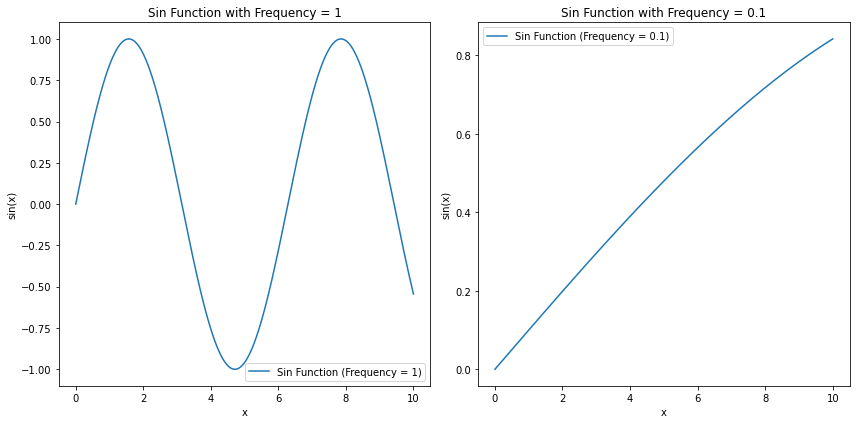
在这张图像上,横坐标是特征的位置编号i,纵坐标是 1 1000 0 2 i d model \frac{1}{10000^{\frac{2i}{d_{\text{model}}}}} 10000dmodel2i1,很显然特征编号越大频率越小。对三角函数来说,频率越小意味着当自变量移动1个单位时,函数值变化越小;频率越高,当自变量移动1个单位时,函数值变化就越剧烈。
python
import numpy as np
import matplotlib.pyplot as plt
# 定义绘制正弦函数的函数
def plot_sin_functions():
y = np.linspace(0, 10, 1000) # 定义 y 轴范围
fig, ays = plt.subplots(1, 2, figsize=(12, 6)) # 创建1y2子图
# 绘制频率为1的正弦函数
frequency1 = 1
y1 = np.sin(frequency1 * y)
ays[0].plot(y, y1, label=f'Sin Function (Frequency = {frequency1})')
ays[0].set_title(f'Sin Function with Frequency = {frequency1}')
ays[0].set_ylabel('y')
ays[0].set_ylabel('sin(y)')
ays[0].legend()
# 绘制频率为0.1的正弦函数
frequency2 = 0.1
y2 = np.sin(frequency2 * y)
ays[1].plot(y, y2, label=f'Sin Function (Frequency = {frequency2})')
ays[1].set_title(f'Sin Function with Frequency = {frequency2}')
ays[1].set_ylabel('y')
ays[1].set_ylabel('sin(y)')
ays[1].legend()
plt.tight_layout()
plt.show()
# 绘制两个正弦函数在横向排列的子图中
plot_sin_functions()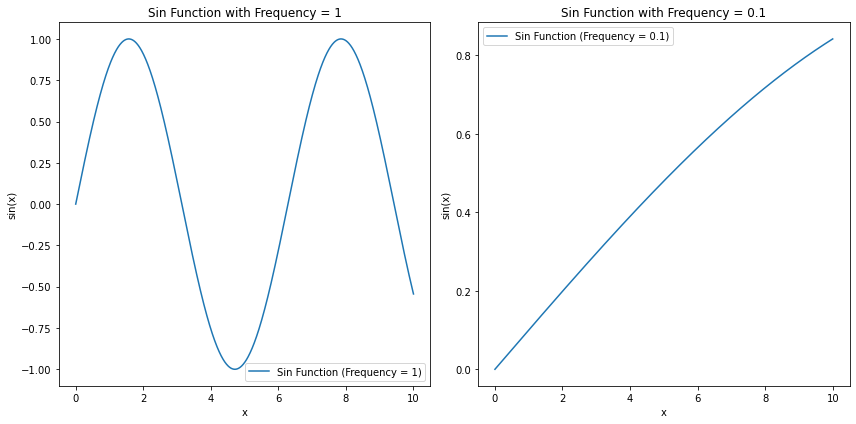
因此,这里你就可以发现非常有趣的事实了------特征编号小的特征,会随着特征值的变化而产生剧烈的变化,即便是相邻的两个样本,在最初的几个特征进行位置编码时,也会产生迥然不同的结果,但是随着特征编号的变大,特征值的变化带来的变化会越来越小,并且会小到呈现出一种单调性(只上升、或者只下降)。当一个信息被映射到这样的高维空间时,我们会认为这个信息的全局趋势和局部细节都被捕捉到了。其中,特征编号比较大的那些维度捕捉到的是样本与样本之间按顺序排列的全局趋势,而特征编号比较小的那些维度捕捉到的是样本与样本的位置之间本身的细节差异。因此,正余弦编码是一种能够同时捕捉到全局位置趋势和细节位置差异的编码方式。
正余弦编码的意义③:通过独特的计算公式,我们可以让特征编号小的特征被投射到剧烈变化的维度上,并且让特征编号大的特征被投射到轻微变化、甚至完全单调的维度上,从而可以让小编号特征去捕捉样本之间的局部细节差异,让大编号特征去捕捉样本之间按顺序排列的全局趋势。
从这个角度来看,其实我们只需要设置一个随着i的增长变得越来越小的公式就可以了,实际公式本身其实并不一定非要是 1 1000 0 2 i d model \frac{1}{10000^{\frac{2i}{d_{\text{model}}}}} 10000dmodel2i1。但这个公式考虑了i相对于特征总量的相对位置,并且还使用了指数函数,它是能够最大程度放大i的影响的公式之一,因此我们使用它可以说是出于一种数学上的便利。当然,你也可以使用其他的公式,只要能够保证i的增长会让频率本身变得越来越小即可。
现在我们可以来看一个具体例子,通过绘制图像来让大家清晰地看到,正余弦编码是如何帮助我们捕捉局部细节和总体趋势的。假设现在有30个样本(索引为1-30),每个样本有4个特征。我们将使用正弦函数编码偶数维度,使用余弦函数编码奇数维度,进行正余弦编码的具体计算。
-
正弦位置编码(
Sinusoidal Positional Encoding)
P E ( p o s , 2 i ) = sin ( p o s 1000 0 2 i d model ) PE_{(pos, 2i)} = \sin \left( \frac{pos}{10000^{\frac{2i}{d_{\text{model}}}}} \right) PE(pos,2i)=sin(10000dmodel2ipos) -
余弦位置编码(
Cosine Positional Encoding)
P E ( p o s , 2 i + 1 ) = cos ( p o s 1000 0 2 i d model ) PE_{(pos, 2i+1)} = \cos \left( \frac{pos}{10000^{\frac{2i}{d_{\text{model}}}}} \right) PE(pos,2i+1)=cos(10000dmodel2ipos)
我请GPT帮我完成了相应的计算流程,最终生成了如下的表单👇
python
import pandas as pd
position = pd.read_csv(r"D:\pythonwork\2024DL\Position_Encoding_for_30_Samples.csv")
python
position| | 维度0 | 维度1 | 维度2 | 维度3 |
| 0 | 0.841471 | 0.540302 | 0.010000 | 0.999950 |
| 1 | 0.909297 | -0.416147 | 0.019999 | 0.999800 |
| 2 | 0.141120 | -0.989992 | 0.029996 | 0.999550 |
| 3 | -0.756802 | -0.653644 | 0.039989 | 0.999200 |
| 4 | -0.958924 | 0.283662 | 0.049979 | 0.998750 |
| 5 | -0.279415 | 0.960170 | 0.059964 | 0.998201 |
| 6 | 0.656987 | 0.753902 | 0.069943 | 0.997551 |
| 7 | 0.989358 | -0.145500 | 0.079915 | 0.996802 |
| 8 | 0.412118 | -0.911130 | 0.089879 | 0.995953 |
| 9 | -0.544021 | -0.839072 | 0.099833 | 0.995004 |
| 10 | -0.999990 | 0.004426 | 0.109778 | 0.993956 |
| 11 | -0.536573 | 0.843854 | 0.119712 | 0.992809 |
| 12 | 0.420167 | 0.907447 | 0.129634 | 0.991562 |
| 13 | 0.990607 | 0.136737 | 0.139543 | 0.990216 |
| 14 | 0.650288 | -0.759688 | 0.149438 | 0.988771 |
| 15 | -0.287903 | -0.957659 | 0.159318 | 0.987227 |
| 16 | -0.961397 | -0.275163 | 0.169182 | 0.985585 |
| 17 | -0.750987 | 0.660317 | 0.179030 | 0.983844 |
| 18 | 0.149877 | 0.988705 | 0.188859 | 0.982004 |
| 19 | 0.912945 | 0.408082 | 0.198669 | 0.980067 |
| 20 | 0.836656 | -0.547729 | 0.208460 | 0.978031 |
| 21 | -0.008851 | -0.999961 | 0.218230 | 0.975897 |
| 22 | -0.846220 | -0.532833 | 0.227978 | 0.973666 |
| 23 | -0.905578 | 0.424179 | 0.237703 | 0.971338 |
| 24 | -0.132352 | 0.991203 | 0.247404 | 0.968912 |
| 25 | 0.762558 | 0.646919 | 0.257081 | 0.966390 |
| 26 | 0.956376 | -0.292139 | 0.266731 | 0.963771 |
| 27 | 0.270906 | -0.962606 | 0.276356 | 0.961055 |
| 28 | -0.663634 | -0.748058 | 0.285952 | 0.958244 |
| 29 | -0.988032 | 0.154251 | 0.295520 | 0.955336 |
|---|
python
position.may()
bash
维度0 0.990607
维度1 0.991203
维度2 0.295520
维度3 0.999950
dtype: float64
python
position.min()
bash
维度0 -0.999990
维度1 -0.999961
维度2 0.010000
维度3 0.955336
dtype: float64在这个表单中,有4个特征全部进行正余弦编码后的结果,很显然,特征编号较小的特征(1和2特征)波动很大,但是特征编号相对较大的特征(3和4)波动就不是那么大。我们只计算了4个特征,是因为我们要绘制的3d图像只能够容纳3个特征,事实上当特征数量变得很多时,大部分特征都会呈现像特征3和特征4一样这样平缓的变化方式。
为了展现局部特征和整体趋势的捕捉,我们使用特征2、3、4来绘制了3D图像,在图像中,我们可以明显地看到局部细节和总体趋势的捕捉👇
python
import plotly.graph_objs as go
import pandas as pd
# 数据
import pandas as pd
position = pd.read_csv(r"D:\pythonwork\2024DL\Position_Encoding_for_30_Samples.csv")
# 绘制3D散点图
fig = go.Figure(data=[go.Scatter3d(
x=position['维度1'],
y=position['维度2'],
z=position['维度3'],
mode='markers',
marker=dict(
size=6,
color=position['维度3'], # 设置颜色为维度3
colorscale='Viridis', # 颜色范围
opacity=1),
text=position.index.tolist(), # 添加样本编号作为文本标签
textposition='top center'
)])
fig.update_layout(
title='3D Scatter Plot',
scene=dict(
xaxis=dict(title='维度1', range=[-1.5, 1.5]),
yaxis=dict(title='维度2', range=[0, 0.3]),
zaxis=dict(title='维度3', range=[0.95, 1])
),
width=800, # 调整图像宽度
height=800 # 调整图像高度
)
fig.show()但除此之外,正余弦编码还有一些额外的好处------
-
首先最重要的是其函数的周期性带来泛化性:在模型训练过程中,我们可能使用的都是序列长度小于20的数据,但是当实际应用中遇到一个序列长度为50的数据,正弦和余弦函数的周期性意味着,即使模型在训练时未见过某个位置,它仍然可以生成一个合理的位置编码。它可用泛化到不同长度的序列。
-
不增加额外的训练参数:当我们在一个已经很大的模型(如 GPT-3 或 BERT)上添加位置信息时,我们不希望增加太多的参数,因为这会增加训练成本和过拟合的风险。正弦和余弦位置编码不增加任何训练参数。
-
即便是相同频率下的正余弦函数,也可以通过周期性带来部分的相对位置信息,可以比绝对位置信息更有效:正弦和余弦函数的周期性特征为模型提供了一种隐含的相对位置信息,使得模型能够更有效地理解序列中不同位置之间的相对关系。
python
import numpy as np
import matplotlib.pyplot as plt
# 定义绘制正弦函数的函数
def plot_sin_functions():
y = np.linspace(0, 10, 1000) # 定义 y 轴范围
fig, ays = plt.subplots(1, 2, figsize=(12, 6)) # 创建1y2子图
# 绘制频率为1的正弦函数
frequency1 = 1
y1 = np.sin(frequency1 * y)
ays[0].plot(y, y1, label=f'Sin Function (Frequency = {frequency1})')
ays[0].set_title(f'Sin Function with Frequency = {frequency1}')
ays[0].set_ylabel('y')
ays[0].set_ylabel('sin(y)')
ays[0].legend()
# 绘制频率为0.1的正弦函数
frequency2 = 0.1
y2 = np.sin(frequency2 * y)
ays[1].plot(y, y2, label=f'Sin Function (Frequency = {frequency2})')
ays[1].set_title(f'Sin Function with Frequency = {frequency2}')
ays[1].set_ylabel('y')
ays[1].set_ylabel('sin(y)')
ays[1].legend()
plt.tight_layout()
plt.show()
# 绘制两个正弦函数在横向排列的子图中
plot_sin_functions()