生成模型实战 | 残差流(Residual Flow)详解与实现
-
- [0. 前言](#0. 前言)
- [1. 残差流模型简介](#1. 残差流模型简介)
- [2. 残差流模型核心理论](#2. 残差流模型核心理论)
-
- [2.1 可逆残差网络基础](#2.1 可逆残差网络基础)
- [2.2 无偏对数似然估计](#2.2 无偏对数似然估计)
- [2.3 内存效率优化](#2.3 内存效率优化)
- [2.4 激活函数与 Lipschitz 约束](#2.4 激活函数与 Lipschitz 约束)
- [3. 使用 PyTorch 实现残差流模型](#3. 使用 PyTorch 实现残差流模型)
-
- [3.1 模型构建](#3.1 模型构建)
- [3.2 模型训练](#3.2 模型训练)
- 相关链接
0. 前言
残差流模型 (Residual Flow) 是一种基于归一化流 (Normalizing Flow)的生成模型,它通过一系列可逆的残差变换将简单分布(如高斯分布)转换为复杂的数据分布。与传统的归一化流不同,残差流使用残差连接来构建可逆变换,这使得模型能够构建更深的网络结构。在本节中,我们将介绍残差流模型的基本原理并使用 PyTorch 从零开始实现残差流模型。
1. 残差流模型简介
归一化流 (Normalizing Flow)模型通过可逆变换 f θ f_{\theta} fθ 把数据 x x x 映射到简单分布 z z z (比如标准正态),利用变换的 Jacobian 行列式计算精确概率密度 l o g p ( x ) = l o g p z ( f ( x ) ) + l o g ∣ d e t d f ( x ) d x ∣ logp(x)=logp_z(f(x))+log|det\frac {df(x)}{dx}| logp(x)=logpz(f(x))+log∣detdxdf(x)∣。但传统可逆设计需要特定结构以便高效计算行列式。
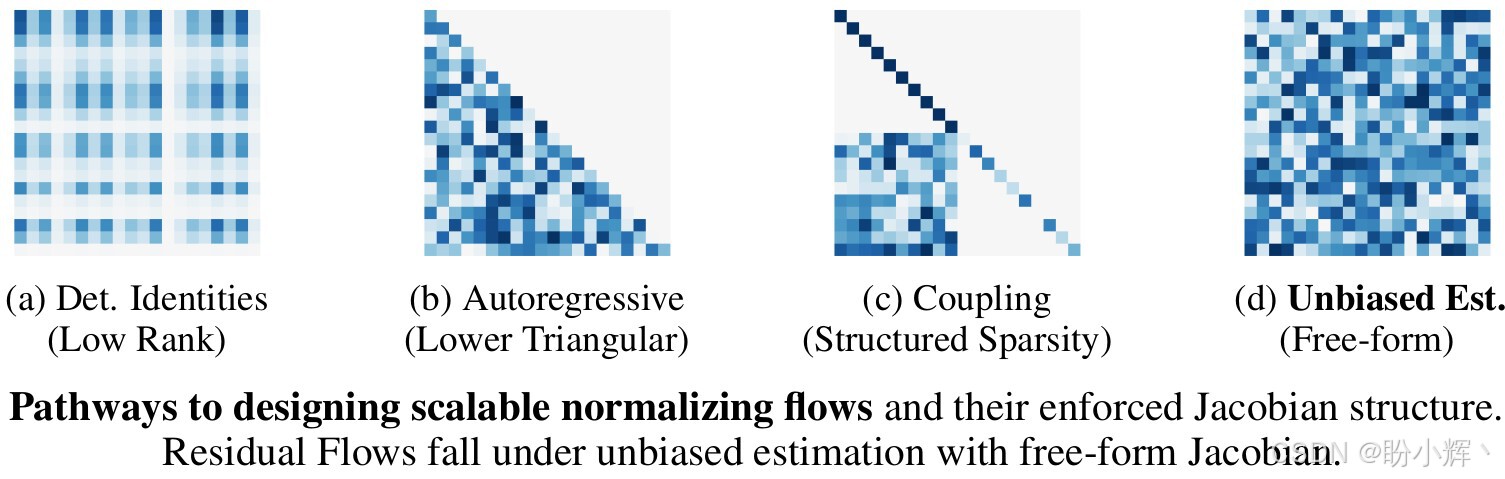
传统的基于流的模型通过使用具有稀疏或结构化雅可比矩阵的受限变换来实现,而残差流模型 (Residual Flow) 是一种基于可逆残差网络的生成建模方法,该方法解决了深度生成模型中似然估计偏差和内存消耗巨大两个关键问题,属于具有自由形式雅可比矩阵的无偏估计方法(如下图所示),成为流模型 (Flow-based Model) 发展中的重要里程碑。
与变分自编码器 (Variational Auto-Encoder, VAE)和生成对抗网络 (Generative Adversarial Network, GAN)等深度生成模型相比,残差流模型具有精确的似然计算、高效的内存利用和稳定的训练过程等优势。该方法的核心思想是利用常微分方程 (Ordinary Differential Equation, ODE) 来构建可逆变换,通过残差网络来学习这一变换。残差流模型的提出极大地推动了可逆生成模型的发展,特别是在需要精确密度估计的任务中表现出色。
此外与需要特殊架构约束的传统流模型(如 RealNVP、Glow )不同,残差流在保留残差网络经典结构的同时,通过施加适当的 Lipschitz 约束确保每一层都是可逆的。这种方法允许模型在保持强大表达能力的同时,也能够精确计算似然函数,为深度生成模型提供了新的可能性。
2. 残差流模型核心理论
2.1 可逆残差网络基础
残差流模型建立在可逆残差网络的基础上,其核心结构形式为:
f ( x ) = x + g ( x ) f(x)=x+g(x) f(x)=x+g(x)
其中 g g g 是一个神经网络层,要确保该变换可逆,必须对 g g g 施加 Lipschitz 约束。具体来说,需要满足 L i p ( g ) < 1 Lip(g) < 1 Lip(g)<1,其中 L i p ( ⋅ ) Lip(\cdot) Lip(⋅) 表示 Lipschitz 常数。
Lipschitz 约束的实现有多种方式:一种是谱归一化 (Spectral Normalization),通过控制每一层权重矩阵的谱范数来实现;另一种是梯度惩罚,在训练过程中显式地约束梯度范数。残差流模型通常采用谱归一化,因为它提供了更加严格和稳定的约束。
与传统的残差网络不同,可逆残差网络必须满足全局可逆性,这意味着整个网络的 Lipschitz 常数必须受到严格控制。当 L i p ( g ) < 1 Lip(g) < 1 Lip(g)<1 对于所有网络层成立时,整个残差网络就是可逆的。
2.2 无偏对数似然估计
归一化流模型的核心优势在于能够精确计算数据点的对数似然。对于传统的流模型,这通过变量变换公式实现:
l o g p ( x ) = l o g p ( z ) + l o g ∣ d e t ∂ f ( x ) ∂ x ∣ logp(x)=logp(z)+log|det\frac {\partial f(x)}{\partial x}| logp(x)=logp(z)+log∣det∂x∂f(x)∣
其中 z = f ( x ) z=f(x) z=f(x) 是可逆变换,但对于残差网络,雅可比矩阵的行列式计算面临巨大挑战,因为它涉及到大型高维矩阵。
残差流采用随机截断方法来解决这一问题。具体而言,它利用俄罗斯轮盘赌估计器 (Russian Roulette estimator) 来无偏地估计无限级数:
l o g ∣ d e t ∂ f ( x ) ∂ x ∣ = l o g ∣ d e t ( I + J g ( x ) ) ∣ = t r ( ∑ k = 1 ∞ ( − 1 ) k + 1 k [ J g ( x ) ] k ) log|det\frac {\partial f(x)}{\partial x}|=log|det(I+J_g(x))|=tr(\sum_{k=1}^{\infty}\frac{(-1)^{k+1}}{k}[J_g(x)]^k) log∣det∂x∂f(x)∣=log∣det(I+Jg(x))∣=tr(k=1∑∞k(−1)k+1[Jg(x)]k)
其中 J g ( x ) = ∂ g − 1 ( x ) ∂ x J_g(x)=\frac{\partial g^{-1}(x)}{\partial x} Jg(x)=∂x∂g−1(x) 是 g g g 在 x x x 处的雅可比矩阵。通过随机截断这个级数,并适当设置截断概率,可以得到无偏的估计结果。
这种方法的关键在于:俄罗斯轮盘赌估计器允许在训练过程中动态调整计算复杂度,在保持估计无偏性的同时,最大限度地提高计算效率。与传统固定截断方法相比,这种方法不会引入系统性偏差,确保了模型真正通过最大似然进行训练。
2.3 内存效率优化
训练深度神经网络时,内存消耗是一个常见瓶颈,尤其是需要存储中间激活值以计算梯度的情况。对于深度流模型,这个问题尤为严重,因为计算对数似然需要跟踪整个前向传播的详细计算过程。
残差流通过在对数密度计算过程中实现内存高效的反向传播解决了这一问题。具体来说,它采用两种降低训练期间内存消耗的方法。
Neumann梯度级数法:可以将梯度具体表示为由Neumann级数导出的幂级数,结合俄罗斯轮盘赌与迹估计器,无需对幂级数进行微分,该方法可降低倍内存需求,在使用无偏估计器时尤为关键,无论抽取多少项,内存占用均保持恒定- 前向反向融合:梯度提前计算,通过在前向计算阶段部分执行反向传播,可进一步优化内存,针对每个残差块,我们在前向传播过程中同步计算 ∂ l o g d e t ( I + J g ( x , θ ) ) ∂ θ \frac {\partial log det(I+Jg(x,θ))}{\partial θ} ∂θ∂logdet(I+Jg(x,θ)),随后立即释放计算图占用的内存,在主反向传播阶段仅需将其与 ∂ L ∂ l o g d e t ( I + J g ( x , θ ) ) \frac {\partial \mathcal L}{\partial log det(I+Jg(x,θ))} ∂logdet(I+Jg(x,θ))∂L 相乘
内存优化具有以下优势:首先,它允许训练更深的网络,因为内存不再成为限制因素;其次,它提高了训练速度,减少了内存分配和数据传输的开销。在实际实现中,残差流模型使用自定义的 PyTorch 函数来实现这种内存高效的梯度计算。
2.4 激活函数与 Lipschitz 约束
激活函数在确保 Lipschitz 约束方面起着关键作用。残差流模型引入了 LipSwish 激活函数:
L i p S w i s h ( x ) = x ⋅ σ ( x ) L i p ( σ ) LipSwish(x)=\frac {x⋅σ(x)}{Lip(σ)} LipSwish(x)=Lip(σ)x⋅σ(x)
其中 σ \sigma σ 是 sigmoid 函数, L i p ( σ ) Lip(\sigma) Lip(σ) 是 σ \sigma σ 的 Lipschitz 常数。这种设计既保持了非线性能力,又确保了 Lipschitz 约束。
与 ReLU 等传统激活函数相比,LipSwish 具有连续可导的特性,这有助于提高梯度流动的稳定性,特别是在深层网络中。此外,它的上界有界性也有助于控制 Lipschitz 常数,确保网络的整体可逆性。
在实际应用中,残差流模型还使用了诱导混合范数 (Induced Mixed Norms) 来进一步加强 Lipschitz 约束。这种方法提供了比单一谱归一化更加灵活和强大的约束手段,允许模型在不同部分采用不同的归一化策略。
3. 使用 PyTorch 实现残差流模型
接下来,我们将使用 PyTorch 从零开始实现残差流模型,并使用 MNIST 数据集进行模型训练。
3.1 模型构建
(1) 导入所需库、设置设备与超参数、数据预处理与实用函数:
python
import argparse
import math
import os
import os.path
import numpy as np
from tqdm import tqdm
import gc
import torch
import torch.nn as nn
import torchvision.transforms as transforms
from torchvision.utils import save_image
import torchvision.datasets as vdsets
from resflows.resflow import ResidualFlow
import resflows.utils as utils
import resflows.layers as layers
import resflows.layers.base as base_layers
class MNIST(object):
def __init__(self, dataroot, train=True, transform=None):
self.mnist = vdsets.MNIST(dataroot, train=train, download=True, transform=transform)
def __len__(self):
return len(self.mnist)
@property
def ndim(self):
return 1
def __getitem__(self, index):
return self.mnist[index]
# Arguments
parser = argparse.ArgumentParser()
parser.add_argument('--dataroot', type=str, default='data')
parser.add_argument('--coeff', type=float, default=0.98)
parser.add_argument('--vnorms', type=str, default='2222')
parser.add_argument('--sn-tol', type=float, default=1e-3)
parser.add_argument('--idim', type=int, default=512)
parser.add_argument('--nblocks', type=str, default='16-16-16')
parser.add_argument('--fc', type=eval, default=False, choices=[True, False])
parser.add_argument('--kernels', type=str, default='3-1-3')
parser.add_argument('--fc-idim', type=int, default=128)
parser.add_argument('--first-resblock', type=eval, choices=[True, False], default=True)
parser.add_argument('--nepochs', help='Number of epochs for training', type=int, default=1000)
parser.add_argument('--batchsize', help='Minibatch size', type=int, default=64)
parser.add_argument('--lr', help='Learning rate', type=float, default=1e-3)
parser.add_argument('--warmup-iters', type=int, default=1000)
parser.add_argument('--save', help='directory to save results', type=str, default='experiment1')
parser.add_argument('--val-batchsize', help='minibatch size', type=int, default=200)
# Dataset and hyperparameters
im_dim = 1
init_layer = LogitTransform(1e-6)
imagesize = 28
train_loader = torch.utils.data.DataLoader(
MNIST(
args.dataroot, train=True, transform=transforms.Compose([
transforms.Resize(imagesize),
transforms.ToTensor(),
add_noise,
])
),
batch_size=args.batchsize,
shuffle=True,
num_workers=4,
)
test_loader = torch.utils.data.DataLoader(
MNIST(
args.dataroot, train=False, transform=transforms.Compose([
transforms.Resize(imagesize),
transforms.ToTensor(),
add_noise,
])
),
batch_size=args.val_batchsize,
shuffle=False,
num_workers=4,
)
print('Creating model.')
input_size = (args.batchsize, im_dim, imagesize, imagesize)
dataset_size = len(train_loader.dataset)(2) 实现 ResidualBlock,包含谱归一化与缩放保证 Lipschitz:
python
class iResBlock(nn.Module):
def __init__(
self,
nnet,
geom_p=0.5,
lamb=2.,
n_samples=1,
n_exact_terms=2,
):
nn.Module.__init__(self)
self.nnet = nnet
self.geom_p = nn.Parameter(torch.tensor(np.log(geom_p) - np.log(1. - geom_p)))
self.lamb = nn.Parameter(torch.tensor(lamb))
self.n_samples = n_samples
self.n_exact_terms = n_exact_terms
# store the samples of n.
self.register_buffer('last_n_samples', torch.zeros(self.n_samples))
self.register_buffer('last_firmom', torch.zeros(1))
self.register_buffer('last_secmom', torch.zeros(1))
def forward(self, x, logpx=None):
if logpx is None:
y = x + self.nnet(x)
return y
else:
g, logdetgrad = self._logdetgrad(x)
return x + g, logpx - logdetgrad
def inverse(self, y, logpy=None):
x = self._inverse_fixed_point(y)
if logpy is None:
return x
else:
return x, logpy + self._logdetgrad(x)[1]
def _inverse_fixed_point(self, y, atol=1e-5, rtol=1e-5):
x, x_prev = y - self.nnet(y), y
i = 0
tol = atol + y.abs() * rtol
while not torch.all((x - x_prev)**2 / tol < 1):
x, x_prev = y - self.nnet(x), x
i += 1
if i > 1000:
logger.info('Iterations exceeded 1000 for inverse.')
break
return x
def _logdetgrad(self, x):
"""Returns g(x) and logdet|d(x+g(x))/dx|."""
with torch.enable_grad():
if (not self.training) and (x.ndimension() == 2 and x.shape[1] == 2):
x = x.requires_grad_(True)
g = self.nnet(x)
# Brute-force logdet only available for 2D.
jac = batch_jacobian(g, x)
batch_dets = (jac[:, 0, 0] + 1) * (jac[:, 1, 1] + 1) - jac[:, 0, 1] * jac[:, 1, 0]
return g, torch.log(torch.abs(batch_dets)).view(-1, 1)
lamb = self.lamb.item()
sample_fn = lambda m: poisson_sample(lamb, m)
rcdf_fn = lambda k, offset: poisson_1mcdf(lamb, k, offset)
if self.training:
# Unbiased estimation.
lamb = self.lamb.item()
n_samples = sample_fn(self.n_samples)
n_power_series = max(n_samples) + self.n_exact_terms
coeff_fn = lambda k: 1 / rcdf_fn(k, self.n_exact_terms) * \
sum(n_samples >= k - self.n_exact_terms) / len(n_samples)
else:
# Unbiased estimation with more exact terms.
lamb = self.lamb.item()
n_samples = sample_fn(self.n_samples)
n_power_series = max(n_samples) + 20
coeff_fn = lambda k: 1 / rcdf_fn(k, 20) * \
sum(n_samples >= k - 20) / len(n_samples)
vareps = torch.randn_like(x)
# Choose the type of estimator.
if self.training:
estimator_fn = neumann_logdet_estimator
else:
estimator_fn = basic_logdet_estimator
# Do backprop-in-forward to save memory.
if self.training:
g, logdetgrad = mem_eff_wrapper(
estimator_fn, self.nnet, x, n_power_series, vareps, coeff_fn, self.training
)
else:
x = x.requires_grad_(True)
g = self.nnet(x)
logdetgrad = estimator_fn(g, x, n_power_series, vareps, coeff_fn, self.training)
if self.training:
self.last_n_samples.copy_(torch.tensor(n_samples).to(self.last_n_samples))
estimator = logdetgrad.detach()
self.last_firmom.copy_(torch.mean(estimator).to(self.last_firmom))
self.last_secmom.copy_(torch.mean(estimator**2).to(self.last_secmom))
return g, logdetgrad.view(-1, 1)
def extra_repr(self):
return 'n_samples={}'.format(
self.n_samples
)(3) 使用 torch.autograd.grad 计算 J g ( x ) v J_g(x)v Jg(x)v,这是 `Hutchinson`` 随机迹估计的核心操作:
python
def batch_jacobian(g, x):
jac = []
for d in range(g.shape[1]):
jac.append(torch.autograd.grad(torch.sum(g[:, d]), x, create_graph=True)[0].view(x.shape[0], 1, x.shape[1]))
return torch.cat(jac, 1)(4) 实现 StackediResBlocks 封装 f ( x ) = x + g ( x ) f(x)=x+g(x) f(x)=x+g(x),包含正向计算、逆向求解:
python
class StackediResBlocks(layers.SequentialFlow):
def __init__(
self,
initial_size,
idim,
squeeze=True,
init_layer=None,
n_blocks=1,
fc=False,
coeff=0.9,
vnorms='122f',
sn_atol=None,
sn_rtol=None,
kernels='3-1-3',
fc_nblocks=4,
fc_idim=128,
first_resblock=False,
):
chain = []
# Parse vnorms
ps = []
for p in vnorms:
if p == 'f':
ps.append(float('inf'))
else:
ps.append(float(p))
domains, codomains = ps[:-1], ps[1:]
assert len(domains) == len(kernels.split('-'))
def _actnorm(size, fc):
if fc:
return FCWrapper(layers.ActNorm1d(size[0] * size[1] * size[2]))
else:
return layers.ActNorm2d(size[0])
def _lipschitz_layer(fc):
return base_layers.get_linear if fc else base_layers.get_conv2d
def _resblock(initial_size, fc, idim=idim, first_resblock=False):
if fc:
return layers.iResBlock(
FCNet(
input_shape=initial_size,
idim=idim,
lipschitz_layer=_lipschitz_layer(True),
nhidden=len(kernels.split('-')) - 1,
coeff=coeff,
domains=domains,
codomains=codomains,
sn_atol=sn_atol,
sn_rtol=sn_rtol,
)
)
else:
ks = list(map(int, kernels.split('-')))
_domains = domains
_codomains = codomains
nnet = []
if not first_resblock:
nnet.append(Swish())
nnet.append(
_lipschitz_layer(fc)(
initial_size[0], idim, ks[0], 1, ks[0] // 2, coeff=coeff,
domain=_domains[0], codomain=_codomains[0], atol=sn_atol, rtol=sn_rtol
)
)
nnet.append(Swish())
for i, k in enumerate(ks[1:-1]):
nnet.append(
_lipschitz_layer(fc)(
idim, idim, k, 1, k // 2, coeff=coeff,
domain=_domains[i + 1], codomain=_codomains[i + 1], atol=sn_atol, rtol=sn_rtol
)
)
nnet.append(Swish())
nnet.append(
_lipschitz_layer(fc)(
idim, initial_size[0], ks[-1], 1, ks[-1] // 2, coeff=coeff,
domain=_domains[-1], codomain=_codomains[-1], atol=sn_atol, rtol=sn_rtol
)
)
return layers.iResBlock(
nn.Sequential(*nnet)
)
if init_layer is not None: chain.append(init_layer)
if first_resblock: chain.append(_actnorm(initial_size, fc))
if squeeze:
c, h, w = initial_size
for i in range(n_blocks):
chain.append(_resblock(initial_size, fc, first_resblock=first_resblock and (i == 0)))
chain.append(_actnorm(initial_size, fc))
chain.append(layers.SqueezeLayer(2))
else:
for _ in range(n_blocks):
chain.append(_resblock(initial_size, fc))
chain.append(_actnorm(initial_size, fc))
# Use four fully connected layers at the end.
for _ in range(fc_nblocks):
chain.append(_resblock(initial_size, True, fc_idim))
chain.append(_actnorm(initial_size, True))
super(StackediResBlocks, self).__init__(chain)(5) 实现 ResidualFlow 把若干残差块串联起来:
python
class ResidualFlow(nn.Module):
def __init__(
self,
input_size,
n_blocks=[16, 16],
intermediate_dim=64,
init_layer=None,
fc=False,
coeff=0.9,
vnorms='122f',
sn_atol=None,
sn_rtol=None,
kernels='3-1-3',
fc_idim=128,
first_resblock=False,
):
super(ResidualFlow, self).__init__()
self.n_scale = min(len(n_blocks), self._calc_n_scale(input_size))
self.n_blocks = n_blocks
self.intermediate_dim = intermediate_dim
self.init_layer = init_layer
self.fc = fc
self.coeff = coeff
self.vnorms = vnorms
self.sn_atol = sn_atol
self.sn_rtol = sn_rtol
self.kernels = kernels
self.fc_idim = fc_idim
self.first_resblock = first_resblock
if not self.n_scale > 0:
raise ValueError('Could not compute number of scales for input of' 'size (%d,%d,%d,%d)' % input_size)
self.transforms = self._build_net(input_size)
self.dims = [o[1:] for o in self.calc_output_size(input_size)]
def _build_net(self, input_size):
_, c, h, w = input_size
transforms = []
_stacked_blocks = StackediResBlocks
for i in range(self.n_scale):
transforms.append(
_stacked_blocks(
initial_size=(c, h, w),
idim=self.intermediate_dim,
squeeze=(i < self.n_scale - 1), # don't squeeze last layer
init_layer=self.init_layer if i == 0 else None,
n_blocks=self.n_blocks[i],
fc=self.fc,
coeff=self.coeff,
vnorms=self.vnorms,
sn_atol=self.sn_atol,
sn_rtol=self.sn_rtol,
kernels=self.kernels,
fc_idim=self.fc_idim,
first_resblock=self.first_resblock and (i == 0)
)
)
c, h, w = c * 4, h // 2, w // 2
return nn.ModuleList(transforms)
def _calc_n_scale(self, input_size):
_, _, h, w = input_size
n_scale = 0
while h >= 4 and w >= 4:
n_scale += 1
h = h // 2
w = w // 2
return n_scale
def calc_output_size(self, input_size):
n, c, h, w = input_size
k = self.n_scale - 1
return [[n, c * 4**k, h // 2**k, w // 2**k]]
def forward(self, x, logpx=None, inverse=False):
if inverse:
return self.inverse(x, logpx)
out = []
for idx in range(len(self.transforms)):
if logpx is not None:
x, logpx = self.transforms[idx].forward(x, logpx)
else:
x = self.transforms[idx].forward(x)
out.append(x)
out = torch.cat([o.view(o.size()[0], -1) for o in out], 1)
output = out if logpx is None else (out, logpx)
return output
def inverse(self, z, logpz=None):
z = z.view(z.shape[0], *self.dims[-1])
for idx in range(len(self.transforms) - 1, -1, -1):
if logpz is None:
z = self.transforms[idx].inverse(z)
else:
z, logpz = self.transforms[idx].inverse(z, logpz)
return z if logpz is None else (z, logpz)3.2 模型训练
(1) 定义训练循环:
python
def train(epoch, model):
model.train()
for i, (x, y) in enumerate(train_loader):
global_itr = epoch * len(train_loader) + i
update_lr(optimizer, global_itr)
x = x.to(device)
beta = 1.
bpd, logpz, neg_delta_logp = compute_loss(x, model, beta=beta)
firmom, secmom = estimator_moments(model)
bpd_meter.update(bpd.item())
logpz_meter.update(logpz.item())
deltalogp_meter.update(neg_delta_logp.item())
firmom_meter.update(firmom)
secmom_meter.update(secmom)
# compute gradient and do SGD step
loss = bpd
loss.backward()
grad_norm = torch.nn.utils.clip_grad.clip_grad_norm_(model.parameters(), 1.)
optimizer.step()
optimizer.zero_grad()
update_lipschitz(model)
ema.apply()
gnorm_meter.update(grad_norm)
if i % 20 == 0:
s = (
'Epoch: [{0}][{1}/{2}] | '
'GradNorm {gnorm_meter.avg:.2f}'.format(
epoch, i, len(train_loader), gnorm_meter=gnorm_meter
)
)
s += (
' | Bits/dim {bpd_meter.val:.4f}({bpd_meter.avg:.4f}) | '
'Logpz {logpz_meter.avg:.0f} | '
'-DeltaLogp {deltalogp_meter.avg:.0f} | '
'EstMoment ({firmom_meter.avg:.0f},{secmom_meter.avg:.0f})'.format(
bpd_meter=bpd_meter, logpz_meter=logpz_meter, deltalogp_meter=deltalogp_meter,
firmom_meter=firmom_meter, secmom_meter=secmom_meter
)
)
print(s)
if i % 500 == 0:
visualize(epoch, model, i, x)
del x
torch.cuda.empty_cache()
gc.collect()(2) 定义可视化函数:
python
def visualize(epoch, model, itr, real_imgs):
model.eval()
real_imgs = real_imgs[:32]
_real_imgs = real_imgs
with torch.no_grad():
# reconstructed real images
recon_imgs = model(model(real_imgs.view(-1, *input_size[1:])), inverse=True).view(-1, *input_size[1:])
# random samples
fake_imgs = model(fixed_z, inverse=True).view(-1, *input_size[1:])
fake_imgs = fake_imgs.view(-1, im_dim, imagesize, imagesize)
recon_imgs = recon_imgs.view(-1, im_dim, imagesize, imagesize)
imgs = torch.cat([_real_imgs, fake_imgs, recon_imgs], 0)
filename = os.path.join(args.save, 'imgs', 'e{:03d}_i{:06d}.png'.format(epoch, itr))
save_image(imgs.cpu().float(), filename, nrow=16, padding=2)
model.train()(3) 定义主函数:
python
def main():
global best_test_bpd
lipschitz_constants = []
ords = []
for epoch in range(args.nepochs):
print('Current LR {}'.format(optimizer.param_groups[0]['lr']))
train(epoch, model)
lipschitz_constants.append(get_lipschitz_constants(model))
ords.append(get_ords(model))
print('Lipsh: {}'.format(pretty_repr(lipschitz_constants[-1])))
print('Order: {}'.format(pretty_repr(ords[-1])))
test_bpd = validate(epoch, model)
if test_bpd < best_test_bpd:
best_test_bpd = test_bpd
utils.save_checkpoint({
'state_dict': model.state_dict(),
'optimizer_state_dict': optimizer.state_dict(),
'args': args,
'ema': ema,
'test_bpd': test_bpd,
}, os.path.join(args.save, 'models'), epoch)
torch.save({
'state_dict': model.state_dict(),
'optimizer_state_dict': optimizer.state_dict(),
'args': args,
'ema': ema,
'test_bpd': test_bpd,
}, os.path.join(args.save, 'models', 'most_recent.pth'))
if __name__ == '__main__':
main()(4) 使用以下命令执行训练过程:
shell
$ python train_img.py --wd 0 --save experiments/mnist --batchsize 32训练过程中,可视化图像如下所示,其中前两行是数据集样本图像,中间两行为模型生成图像,最后两行为重建图像:

相关链接
生成模型实战 | 生成模型(Generative Model)基础
生成模型实战 | 归一化流模型(Normalizing Flow Model)
生成模型实战 | GLOW详解与实现
生成模型实战 | 自回归流MAF详解与实现