【码道初阶】【Leetcode105&106】用遍历序列还原二叉树：前序+中序、后序+中序的统一套路与“先建哪边”的坑

【Leetcode105&106】用遍历序列还原二叉树：前序+中序、后序+中序的统一套路与"先建哪边"的坑

二叉树的遍历序列题，特别像"看上去是模板题，但真正拉开差距的是细节"。很多时候不是不会写，而是写着写着就把"顺序"弄反，结果要么构出来的树不对，要么直接递归爆栈。

做这类题，我习惯先把两件事牢牢记住：

1. 前序 / 后序序列负责告诉我：根节点是谁
2. 中序序列负责告诉我：左子树和右子树的边界在哪里

接下来就交给递归：每次在中序区间里切一刀，把大问题切成左右子树的小问题继续做。

这篇文章把两道题放在一起讲：

• 题目 A：前序 preorder + 中序 inorder 构造树
• 题目 B：中序 inorder + 后序 postorder 构造树

并且会重点解释一个非常高频的问题（也是最容易踩坑的地方）：

为什么在"后序+中序"构造树里，递归必须先构建 right 再构建 left？

如果把 left 放前面，为什么会直接 StackOverflow？

---

一、 Leetcode105：preorder + inorder 构造二叉树

题目回顾

给两个数组：

• preorder：先序遍历（根 → 左 → 右）
• inorder：中序遍历（左 → 根 → 右）

要求构造原二叉树并返回根节点。

示例：

• preorder = [3,9,20,15,7]
• inorder = [9,3,15,20,7]
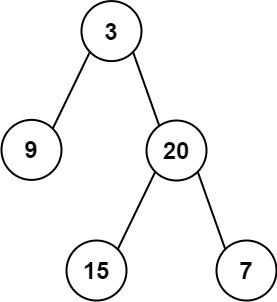
  输出树层序：[3,9,20,null,null,15,7]

先序 + 中序的关键结论

这里的思路非常"干脆"：

• 先序的第一个元素一定是当前子树的根
• 在中序里找到这个根的位置，就能把中序分成：左半段=左子树，右半段=右子树

---

二、来看这段代码（题目 Leetcode105 的实现）

class Solution {
    public int preindex = 0;

    public TreeNode buildTree(int[] preorder, int[] inorder) {
        return buildChildTree(preorder, inorder, 0, inorder.length - 1);
    }

    public TreeNode buildChildTree(int[] preorder, int[] inorder, int ibegin, int iend) {
        if (ibegin > iend) return null;

        TreeNode root = new TreeNode(preorder[preindex]);
        int rootIndex = findval(inorder, ibegin, iend, preorder[preindex]);
        preindex++;

        root.left = buildChildTree(preorder, inorder, ibegin, rootIndex - 1);
        root.right = buildChildTree(preorder, inorder, rootIndex + 1, iend);
        return root;
    }

    private int findval(int[] inorder, int ibegin, int iend, int val) {
        for (int i = ibegin; i <= iend; i++) {
            if (inorder[i] == val) return i;
        }
        return -1;
    }
}

这段代码的整体思路（拆成三句话）

把它当成一个"递归工厂"，每次负责生产一棵子树：

1. preindex 永远指向"当前子树的根"，因为先序是"根左右"
2. 在 inorder[ibegin..iend] 中找到根的位置 rootIndex
3. 递归构建左区间和右区间，最后把它们挂到 root 上

为什么这里是"先构建 left，再构建 right"？

原因很本质：先序遍历的顺序就是：

根 → 左 → 右

根节点用掉之后，preindex 指向的下一个节点就是左子树的根。如果这时候先去建右子树，那就相当于拿着左子树的根去右区间里找，必然错位。

所以题目 A 的顺序必须是：

root.left  = ...
root.right = ...

---

三、题目 B：inorder + postorder 构造二叉树

题目回顾

给两个数组：

• inorder：中序遍历（左 → 根 → 右）
• postorder：后序遍历（左 → 右 → 根）

要求构造原二叉树并返回根节点。

示例：

• inorder = [9,3,15,20,7]
• postorder = [9,15,7,20,3]
  输出树层序：[3,9,20,null,null,15,7]

后序 + 中序的关键结论

这里同样抓住"根"和"切割"两件事：

• 后序的最后一个元素一定是当前子树的根
• 中序切分方式仍然一样：左边是左子树，右边是右子树
• 但这里有一个超级关键点：如果从后往前消费 postorder，顺序是"根 → 右 → 左"

为什么会这样？因为后序是：左 → 右 → 根

倒过来读就是：根 → 右 → 左

这个"倒序的顺序"就是题目 B 的坑点核心。

---

四、来看这段代码（Leetcode106 的实现）

class Solution {
    public int preindex = 0;

    public TreeNode buildTree(int[] inorder, int[] postorder) {
        preindex = postorder.length - 1;
        return buildChildTree(postorder, inorder, 0, inorder.length - 1);
    }

    public TreeNode buildChildTree(int[] postorder, int[] inorder, int ibegin, int iend) {
        if (ibegin > iend) return null;

        TreeNode root = new TreeNode(postorder[preindex]);
        int rootIndex = findval(inorder, ibegin, iend, postorder[preindex]);
        if (preindex > 0) preindex--;

        root.right = buildChildTree(postorder, inorder, rootIndex + 1, iend);
        root.left  = buildChildTree(postorder, inorder, ibegin, rootIndex - 1);

        return root;
    }

    private int findval(int[] inorder, int ibegin, int iend, int val) {
        for (int i = ibegin; i <= iend; i++) {
            if (inorder[i] == val) return i;
        }
        return -1;
    }
}

这段代码的整体思路（仍然是同一套路）

如果只看骨架，会发现它和题目 A 非常像：

1. preindex 从 postorder 的最后开始走：每次取当前根
2. 在 inorder 切出左右子树区间
3. 递归构建左右子树并挂上去

真正的差别只有一个点（但这个点能决定生死）：

• 题目 A：preindex 从左往右走，根之后是左子树
• 题目 B：preindex 从右往左走，根之后是右子树

于是就引出了那个关键疑问。

---

五、关键疑问：为什么题目 Leetcode106 不能先构建 left？

问题说得再具体一点：

如果把这两行交换顺序
root.left = ... 放到 root.right = ... 前面

就会 StackOverflow；换回来又好了。为什么？

答案一句话就够：

因为倒序 postorder 的消费顺序是"根 → 右 → 左"，如果先构建 left，就会拿"右子树的根"去左区间里找，找不到导致 rootIndex = -1，区间无法正确缩小，递归不收敛，最终爆栈。

下面把这个"爆栈链条"详细展开（这部分是理解的关键）。

---

六、爆栈是怎么发生的：错位消费 + 找不到根 + 区间不收缩

用示例来走一次：

• inorder [9, 3, 15, 20, 7]
• postorder [9, 15, 7, 20, 3]

初始化 preindex = 4，指向 3。

1）第一步：取根 3 没问题

• root = 3

• 在 inorder 找到 3 的位置：rootIndex = 1

  切分：

  • 左区间 [0..0] → [9]
  • 右区间 [2..4] → [15,20,7]

• preindex-- 指向 20（注意：下一位是 20）

2）如果先构建 left，就直接错位

此时 preindex 指向的是 20 ，但左区间里只有 9。

如果先递归构建 left，会做：

• root = postorder[preindex] = 20
• 然后在 inorder 的左区间 [9] 里找 20
• 找不到 → findval 返回 -1

3）rootIndex = -1 会引发致命后果

接下来递归会用 rootIndex 去计算左右区间：

• 右区间：rootIndex + 1 .. iend → 0 .. iend
• 左区间：ibegin .. rootIndex - 1 → ibegin .. -2

左区间很快会因为 ibegin > iend 返回 null，这还好。

但右区间变成了 0..iend ------ 很可能比当前区间还大或几乎没变，递归规模不缩小。

递归能结束依赖的就是这句 base case：

if (ibegin > iend) return null;

可一旦区间不缩小，base case 永远触发不了，就会不断递归下去，最终 StackOverflow。

4）为什么换成先 right 就好了？

因为 preindex-- 后指向的 20，恰好是 右子树的根，右区间也确实包含 20，所以：

• rootIndex 能正确找到
• inorder 区间会不断缩小
• 递归自然收敛
• 整个过程稳定结束

所以题目 B 必须：

root.right = ...
root.left  = ...

这不是"写法偏好"，是由"倒序消费 postorder 的顺序 = 根右左"决定的。

---

七、把两题统一成一个"记忆模型"

如果不想每次都重推，可以只记一个模型（非常好用）：

• 中序 inorder：负责切割左右边界
• 另一种遍历（前序/后序）：负责 warn 我根节点出现的位置
• 消费遍历数组的方向，决定先建哪一边

对应关系：

前序 + 中序

• 前序：根 左 右
• 从左往右消费：根之后是左子树
• 所以：先建 left，再建 right

后序 + 中序

• 后序：左 右 根
• 从右往左消费：根之后是右子树（倒序根右左）
• 所以：先建 right，再建 left

这就是顺序的"根本原因"。

---

八、一个很实用的工程化补充：O(n²) 可以优化到 O(n)

两段代码都用 findval 在 inorder 区间线性扫描找 rootIndex。最坏情况下（树极度不平衡）会退化成 O(n²)。

更稳的做法是：

• 先用 HashMap 把 inorder 的值映射到下标：value -> index
• 每次找 rootIndex 直接 O(1)

n 最大 3000，其实不少平台 O(n²) 也能过，但写成 O(n) 更像"标准答案"。

---

九、小结

这两题的本质是一件事：

1. 先序/后序给出"根"
2. 中序定位根的位置，切成左右子树区间
3. 递归重复
4. 关键差异只有一个：消费遍历序列的方向不同，导致必须先构建的子树不同

• 前序从左到右：根之后是左 ⇒ 先 left 后 right
• 后序从右到左：根之后是右 ⇒ 先 right 后 left
• 在后序题里如果先建 left，会把右子树根塞进左区间，根下标找不到导致区间不收缩，最后爆栈

这一套想明白之后，类似的题（如"前序+中序还原""后序+中序还原""层序+中序是否可行"等）都会变得非常直观：先问"根从哪来"，再问"中序怎么切"，最后问"谁先被消费"。