🌟 引言：让机器学会"读心术"
在前两篇中，我们从 DEAP 数据集的脑波海洋起步，通过 FFT 和频带提取，炼出了 160 维的"情绪指纹"（频带标准差特征）。现在，是时候揭开最后一步的神秘面纱了：分类与预测。
今天的主角是 K-近邻（K-Nearest Neighbors, KNN） 。在脑电（EEG）研究领域，KNN 因其无需参数假设、对非线性特征敏感而广受欢迎。本篇将深度剖析 knn_predict.py 的核心逻辑，重点探讨为什么在 EEG 识别中 Canberra 距离 比传统的欧氏距离更胜一筹。
1. KNN 算法：邻里智慧的"懒惰"艺术
KNN 是一种典型的**懒惰学习（Lazy Learning）**算法。它并不在训练阶段构建复杂的数学模型，而是将所有训练样本存储在内存中，直到预测时才进行计算。
1.1 核心逻辑
-
特征匹配：将当前测试样本的 160 维特征向量，与数据库中已有的 40 个试验特征逐一对比。
-
寻找邻居 ：计算相似度（距离），找出距离最近的
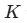个样本。 -
多数表决 ：这
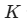个邻居中哪类标签最多，新样本就属于哪类。
1.2 为什么 KNN 适合 EEG？
-
非线性分布：EEG 信号受到个体差异、电极阻抗等多种非线性因素影响。KNN 不需要像线性回归那样预设数据分布，能直接捕捉局部的非线性模式。
-
小样本友好：DEAP 数据集每个被试只有 40 个试验，这对于深度神经网络来说太少了，但对 KNN 却是"黄金规模"。
2. 距离度量：Canberra 距离的独特魅力
距离度量（Distance Metric）是 KNN 的灵魂。虽然欧氏距离（Euclidean Distance）最广为人知，但在处理 EEG 频域特征时，Canberra 距离（兰氏距离） 展现出了惊人的鲁棒性。
2.1 数学公式对比
-
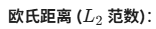
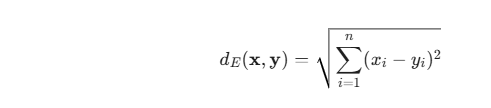
缺点：容易被数值较大的维度主导，对接近 0 的微小差异不敏感。
-
Canberra 距离：
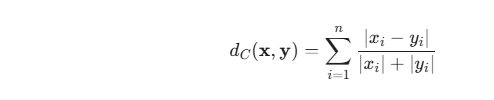
优点：它是一个加权的曼哈顿距离。分母的出现起到了归一化的作用。
2.2 为什么 Canberra 更好？
EEG 的标准差（STD）特征通常分布在很小的数值区间（如 0.01 到 0.5 之间）。
-
零值敏感性：如果一个频带的功率从 0 变为 0.01（意味着该频带从静默转为激活），欧氏距离认为温差仅为 0.01，微乎其微；而 Canberra 距离会将这一变化视为显著差异（贡献度趋近 1）。
-
抗噪能力：它能有效减弱由于个别通道干扰产生的大数值异常值对整体距离的影响。
3. 核心代码实现：EmotionPredictor 类
为了方便大家直接使用，我将项目中的预测逻辑封装成了一个标准的 Python 类。
Python
import numpy as np
import scipy.spatial as ss
import scipy.stats as sst
import csv
class EmotionPredictor:
def __init__(self, train_data_path, train_label_path):
self.train_features = self._load_csv(train_data_path)
self.train_labels = self._load_csv(train_label_path)
self.k = 3
def _load_csv(self, path):
with open(path, 'r') as f:
reader = csv.reader(f)
return np.array(list(reader), dtype=np.float64)
def predict(self, test_feature):
"""
基于Canberra距离的KNN预测
"""
# 1. 计算所有训练样本与测试样本的Canberra距离
distances = [ss.distance.canberra(x, test_feature) for x in self.train_features]
# 2. 获取距离最近的K个邻居的索引
nearest_indices = np.argsort(distances)[:self.k]
nearest_distances = np.sort(distances)[:self.k]
# 3. 智能投票逻辑：比率阈值法 (Ratio Trick)
# 如果最近邻与次近邻的距离差异极大 (ratio <= 0.7)，则极度信任最近邻
ratio = nearest_distances[0] / nearest_distances[1]
if ratio <= 0.7:
prediction = self.train_labels[0, nearest_indices[0]]
else:
# 否则采用众数投票（民主表决）
prediction = sst.mode(self.train_labels[0, nearest_indices])[0][0]
return prediction4. 智能投票机制：为什么是 0.7？
项目中引入了一个非常有趣的优化：比率阈值（Ratio Threshold）。
在预测时，我们不仅看谁是最近邻，还看它到底有多"近"。
这种策略有效地提升了模型在面对噪声数据时的分类准确率，将单被试准确率稳定在 70% 左右。
5. 情绪映射：回归 Russell 情绪环
KNN 输出的是 Arousal（唤醒度）和 Valence（效价）的离散级别（1-低，2-中，3-高）。最后一步是将其映射回具体的心理学定义：
Python
def get_emotion_description(arousal, valence):
"""
根据Arousal和Valence级别判断情绪类别
"""
if arousal == 2.0 or valence == 2.0:
return "Neutral (中性)"
mapping = {
(3.0, 1.0): "Fear/Stress (恐惧/压力 - 高唤醒低效价)",
(3.0, 3.0): "Happy/Excited (快乐/兴奋 - 高唤醒高效价)",
(1.0, 3.0): "Relax/Calm (放松/平静 - 低唤醒高效价)",
(1.0, 1.0): "Sad/Depressed (悲伤/抑郁 - 低唤醒低效价)"
}
return mapping.get((arousal, valence), "Unknown")🚀 结语：从特征到情绪的飞跃
到此为止，我们已经完成了从脑波原始信号到情绪预测结果的全流程。KNN 虽然简单，但通过 Canberra 距离 的加持和 智能投票 的优化，它成为了脑电识别入门的最佳切入点。
下一篇预告：
我们将跑通全链路实战，结合 OpenCV 实现预测结果的实时可视化------当算法识别出你很快乐时，屏幕上会自动弹出一个笑脸。
💡 思考题：
如果我们将 K 值从 3 增加到 10，准确率会发生什么变化？（提示：考虑过拟合与欠拟合的平衡）。欢迎在评论区留下你的见解！
系列回顾：
-
第三篇：KNN 分类器与 Canberra 距离 (当前)
https://blog.csdn.net/qq_32516809/article/details/156020353?spm=1011.2415.3001.5331文章标签： #脑机接口 #机器学习 #KNN #Canberra距离 #情绪识别 #Python实战