有序二叉树(二叉搜索树)的核心特性是左子树节点值 < 根节点值 < 右子树节点值,删除节点时需要保证删除后树的有序性不被破坏。
一、为什么删除有序二叉树节点这么麻烦?
普通二叉树删除节点只需要断开引用,但有序二叉树不行:它的节点值之间有严格的大小关系约束。比如删除一个中间节点后,必须找到合适的节点 "填补空位",同时保证整个树的有序性。
根据目标节点的子节点数量,删除操作可以分为三种核心场景,我们逐个拆解。
二、删除的三种场景
先看一个示例有序二叉树(后续所有例子都基于这棵树):
7
/ \
3 10
/ \ /
1 5 9
/
2场景 1:删除叶子节点(无左右子节点)
叶子节点是树的 "末梢",比如上面树中的2、5、9。
原理:叶子节点没有子节点,删除后不会影响其他节点的关系,只需要断开父节点对它的引用即可。
步骤拆解:
1.找到要删除的目标节点(比如5);
2.找到目标节点的父节点(5的父节点是3);
3.判断目标节点是父节点的左子节点还是右子节点(5是3的右子节点);
4.将父节点对应的子节点引用置为null(把3的右子节点设为null)。

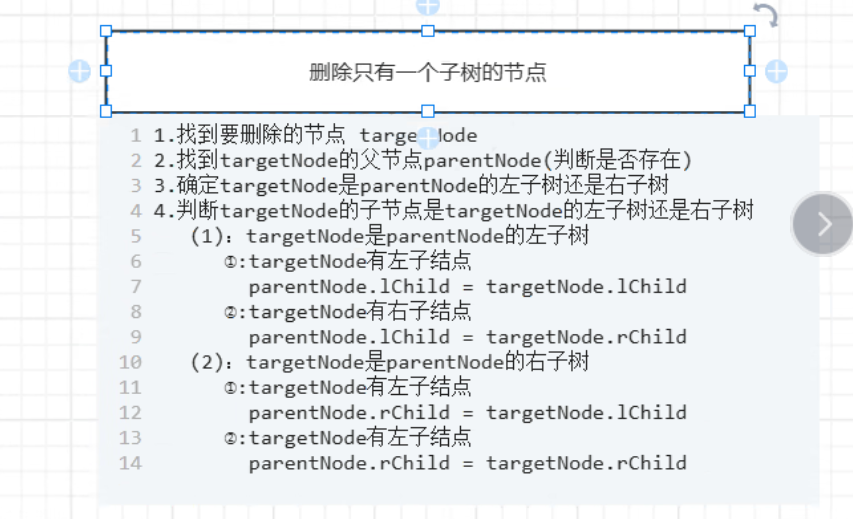
场景 2:删除只有一个子节点的节点
比如树中的1(只有右子节点2)、10(只有左子节点9)。
原理:目标节点有且只有一个子节点,删除后需要让这个子节点 "接替" 目标节点的位置,保持树的连续有序。
步骤拆解 (以删除1为例):
1.找到目标节点1和它的父节点3;
2.确定1是3的左子节点;
3.确定1的子节点是右子节点2;
4.让3的左子节点直接指向2(相当于2接替了1的位置)。
场景 3:删除有两个子节点的节点(最复杂)
比如树中的3(有左子节点1、右子节点5)、7(有左子节点3、右子节点10)。
难点:目标节点有两个子节点,直接删除会导致两个子树 "悬空",无法直接接替位置。
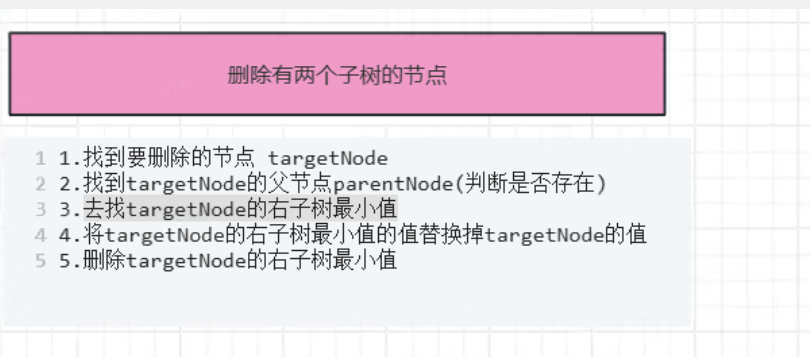
解决方案 :用目标节点右子树的最小值(或左子树的最大值)来替换目标节点的值 ------ 因为右子树的最小值是比目标节点大的节点中最小的那个,替换后能保证树的有序性;而这个最小值节点必然是叶子节点或只有一个子节点(右子树的最小值是最左侧节点),后续删除它就回到了前两种简单场景。
步骤拆解 (以删除3为例):
1.找到目标节点3;
2.找到3的右子树(节点5),并找到该子树的最小值(就是5本身);
3.用5的值替换3的值;
4.删除右子树中的最小值节点5(此时5是叶子节点,回到场景 1 的删除逻辑)。
三、核心工具方法实现
1. 查找父节点 findParent.
要删除节点,必须先找到它的父节点才能修改引用。这个方法通过递归遍历树,利用有序二叉树的 "左小右大" 特性定位父节点。
通过递归遍历树,找到目标节点的父节点:
java
// 查找目标节点的父节点
public TreeNode findParent(TreeNode root, Integer data) {
TreeNode current = root;
if (current == null) {
return null;
}
// 当前节点的左/右子节点是目标节点 → 当前节点是父节点
if ((current.lChild != null && current.lChild.data == data)
|| (current.rChild != null && current.rChild.data == data)) {
return current;
} else {
// 递归查找:根据有序性向左/右子树遍历
if (current.data < data && current.rChild != null) {
return findParent(current.rChild, data);
} else if (current.data > data && current.lChild != null) {
return findParent(current.lChild, data);
} else {
return null; // 未找到父节点(目标节点不存在)
}
}
}逻辑解读:
先判断当前节点的子节点是否是目标节点,如果是,直接返回当前节点;
如果不是,根据目标值和当前节点的大小关系,递归遍历左 / 右子树;
全程要判断子节点是否为空,避免空指针异常。
2. 查找右子树最小值 findRightTreeMin
这个方法是为 "场景 3(两个子节点)" 服务的:找到右子树的最小值,同时删除这个最小值节点(因为后续要拿它替换目标节点的值)。
java
// 查找右子树的最小值,并删除该节点
public int findRightTreeMin(TreeNode node) {
// 遍历到最左侧节点(最小值)
while (node.lChild != null) {
node = node.lChild;
}
int min = node.data;
delete(root, min); // 删除这个最小值节点
return min;
}逻辑解读:
右子树的最小值一定在最左侧(因为左子节点值 < 父节点值);
找到最小值后,调用delete方法删除它(此时删除的是简单场景的节点);
返回这个最小值,用于替换目标节点的值。
四、删除方法完整实现 delete
有了辅助方法,我们可以实现最终的delete方法,把三种删除场景的逻辑整合起来。
首先要明确:实现delete前需要先有find方法(用于查找目标节点),find方法我们再上一篇博客已经实现(逻辑类似findParent,找到目标节点后返回),详情请查看上一篇博客。
java
public void delete(TreeNode root, Integer data) {
if (root == null) {
return;
}
// 特殊情况:树只有根节点,直接置空
if (root.rChild == null && root.lChild == null) {
root = null;
return;
}
// 1. 找到目标节点
TreeNode targetNode = find(root, data);
if (targetNode == null) { // 目标节点不存在
return;
}
// 2. 找到父节点
TreeNode parentNode = findParent(root, data);
// 情况1:删除叶子节点
if (targetNode.rChild == null && targetNode.lChild == null) {
if (parentNode.rChild == targetNode) {
parentNode.rChild = null;
} else if (parentNode.lChild == targetNode) {
parentNode.lChild = null;
}
}
// 情况2:删除有两个子节点的节点
else if (targetNode.rChild != null && targetNode.lChild != null) {
int min = findRightTreeMin(targetNode.rChild);
targetNode.data = min; // 替换目标节点的值
}
// 情况3:删除只有一个子节点的节点
else {
if (parentNode.lChild == targetNode) { // 目标是父节点的左子树
if (targetNode.lChild != null) {
parentNode.lChild = targetNode.lChild;
} else {
parentNode.lChild = targetNode.rChild;
}
} else if (parentNode.rChild == targetNode) { // 目标是父节点的右子树
if (targetNode.lChild != null) {
parentNode.rChild = targetNode.lChild;
} else {
parentNode.rChild = targetNode.rChild;
}
}
}
}五、代码测试
java
package com.qcby.Tree;
public class Test {
public static void main(String[] args) {
BinaryTree bt = new BinaryTree();
bt.create(7);
bt.create(3);
bt.create(10);
bt.create(1);
bt.create(5);
bt.create(9);
bt.create(2);
bt.delete(bt.root, 2); //输出7 3 10 1 5 9 2
bt.levelOrder(bt.root);
bt.delete(bt.root, 1); //输出7 3 10 2 5 9
bt.levelOrder(bt.root);
bt.delete(bt.root, 7); //输出9 3 10 1 5 2
bt.levelOrder(bt.root);
}
}