目录
一:最长递增子序列
1.1题目

题目链接:https://leetcode.cn/problems/longest-increasing-subsequence/description/
1.2算法原理
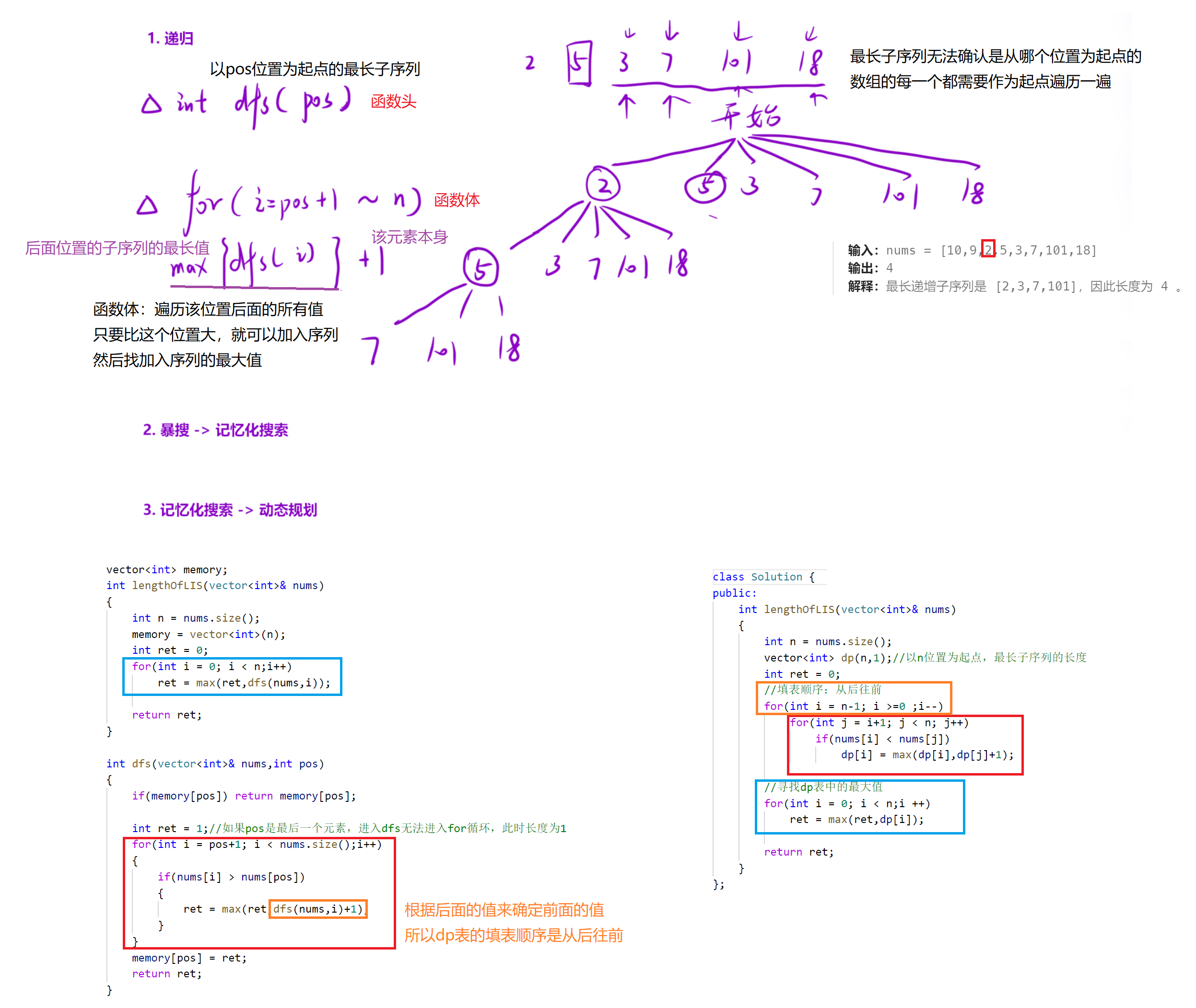
1.3代码
递归版本(运行结果超时)
cpp
class Solution {
public:
int lengthOfLIS(vector<int>& nums)
{
int n = nums.size();
int ret = 0;
for(int i = 0; i < n;i++)
ret = max(ret,dfs(nums,i));
return ret;
}
int dfs(vector<int>& nums,int pos)
{
int ret = 1;//如果pos是最后一个元素,进入dfs无法进入for循环,此时长度为1
for(int i = pos+1; i < nums.size();i++)
{
if(nums[i] > nums[pos])
{
ret = max(ret,dfs(nums,i)+1);
}
}
return ret;
}
};记忆化搜索:
cpp
class Solution {
public:
vector<int> memory;
int lengthOfLIS(vector<int>& nums)
{
int n = nums.size();
memory = vector<int>(n);
int ret = 0;
for(int i = 0; i < n;i++)
ret = max(ret,dfs(nums,i));
return ret;
}
int dfs(vector<int>& nums,int pos)
{
if(memory[pos]) return memory[pos];
int ret = 1;//如果pos是最后一个元素,进入dfs无法进入for循环,此时长度为1
for(int i = pos+1; i < nums.size();i++)
{
if(nums[i] > nums[pos])
{
ret = max(ret,dfs(nums,i)+1);
}
}
memory[pos] = ret;
return ret;
}
};动态规划:
cpp
class Solution {
public:
int lengthOfLIS(vector<int>& nums)
{
int n = nums.size();
vector<int> dp(n,1);//以n位置为起点,最长子序列的长度
int ret = 0;
//填表顺序:从后往前
for(int i = n-1; i >=0 ;i--)
for(int j = i+1; j < n; j++)
if(nums[i] < nums[j])
dp[i] = max(dp[i],dp[j]+1);
//寻找dp表中的最大值
for(int i = 0; i < n;i ++)
ret = max(ret,dp[i]);
return ret;
}
};二:猜数字大小
2.1题目

题目链接:https://leetcode.cn/problems/guess-number-higher-or-lower-ii/
2.2算法原理
2.3代码
记忆化搜索:
cpp
class Solution {
public:
int getMoneyAmount(int n)
{
vector<vector<int>> memory(n+1,vector<int>(n+1));
return dfs(1,n,memory);
}
int dfs(int left, int right,vector<vector<int>>& memory)
{
if(left >= right) return 0;
if(memory[left][right]) return memory[left][right];
int ret = INT_MAX;
//每一种策略:找最小
for(int head = left;head <= right;head++)
{
//具体的策略中,找最大,确保钱不会花完
int l = dfs(left,head-1,memory);
int r = dfs(head+1,right,memory);
ret = min(ret,max(l,r)+head);
}
memory[left][right] = ret;
return ret;
}
};三:矩阵中最长的递增路径
3.1题目

题目链接:https://leetcode.cn/problems/longest-increasing-path-in-a-matrix/description/
3.2算法原理
其他的算法原理和之前文章中的递归题目是一样的
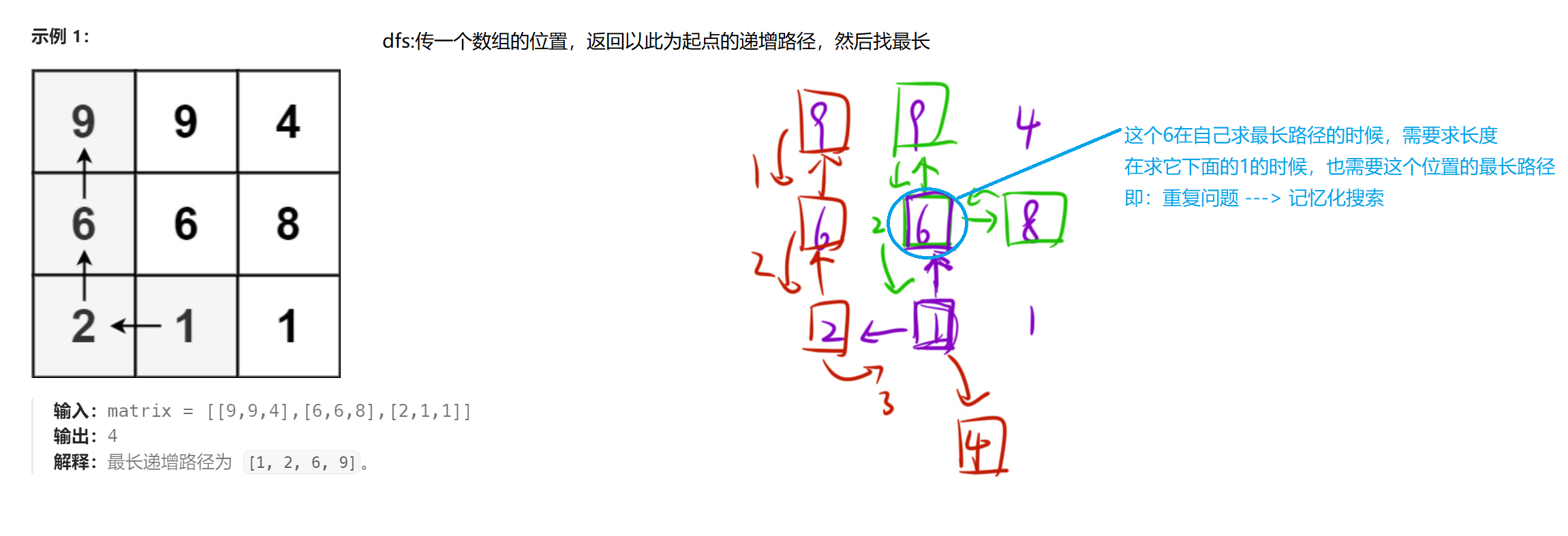
3.3代码
cpp
class Solution {
public:
int dx[4] = { 0,0,1,-1 };
int dy[4] = { -1,1,0,0 };
int m, n;
vector<vector<int>> memory;
int longestIncreasingPath(vector<vector<int>>& matrix)
{
m = matrix.size(), n = matrix[0].size();
memory = vector<vector<int>>(m, vector<int>(n));
for (int i = 0; i < m; i++)
for (int j = 0; j < n; j++)
dfs(matrix, i, j);
int ret = 0;
for (int i = 0; i < m; i++)
for (int j = 0; j < n; j++)
ret = max(ret, memory[i][j]);
return ret;
}
int dfs(vector<vector<int>>& matrix, int i, int j)
{
if (memory[i][j]) return memory[i][j];
int ret = 1;
for (int k = 0; k < 4; k++)
{
int x = i + dx[k], y = j + dy[k];
if (x >= 0 && x < m && y >= 0 && y < n && matrix[x][y] > matrix[i][j])
ret = max(ret, dfs(matrix, x, y) + 1);
}
memory[i][j] = ret;
return ret;
}
};