【数据结构】二叉树进阶：层序遍历不仅是按层打印，更是形态判定的利器！

🏠 个人主页: EXtreme35

📚 个人专栏:

专栏名称	专栏主题简述
《C语言》	C语言基础、语法解析与实战应用
《数据结构》	线性表、树、图等核心数据结构详解
《题解思维》	算法思路、解题技巧与高效编程实践

目录

• • 一、构建基石------队列的链式实现
  • • [1.1 队列结构定义](#1.1 队列结构定义)
    • [1.2 关键接口实现](#1.2 关键接口实现)
  • 二、层序遍历的算法逻辑
  • • [2.1 算法流程](#2.1 算法流程)
    • [2.2 代码实现](#2.2 代码实现)
  • 三、核心进阶------判定完全二叉树
  • • [3.1 洞察：完全二叉树的"连续性"](#3.1 洞察：完全二叉树的“连续性”)
    • [3.2 那些"看似可行"但不适合的经典思路](#3.2 那些“看似可行”但不适合的经典思路)
    • • 避坑思路一：仅通过"节点总数"判断
      • 避坑思路二：仅比较左右子树的高度差
    • [3.3 判定的绝妙思路](#3.3 判定的绝妙思路)
    • • 判定代码实现
  • 四、总结与复杂度分析
  • • [4.1 复杂度](#4.1 复杂度)
    • [4.2 核心要点](#4.2 核心要点)

引言

在二叉树的算法体系中，深度优先遍历（如前、中、后序遍历）通常利用递归实现，其核心在于"纵向深度"。然而，在处理如"按层打印"或"判定树形态"的问题时，我们需要另一种视角------层序遍历（Level Order Traversal）。

层序遍历是一种广度优先搜索（BFS），它按照从上到下、从左到右的顺序访问每一个节点。为了实现这一逻辑，我们需要借助一种"先进先出"的数据结构：队列。

---

一、构建基石------队列的链式实现

在 C 语言中，为了高效地实现层序遍历，我们首先需要构建一个健壮的队列。相比数组，链式队列在频繁入队和出队时具有更好的性能表现。

1.1 队列结构定义

这里参考我之前手撕队列（Queue）的博客。

之前我们只是简单的给每个节点存储了int值，这时候就体现出typedef的优点了，现在队列的每个节点存储的是二叉树节点的指针 struct BinTreeNode*，只需要修改一行代码就可以。

typedef struct BinTreeNode* QDataType;

而队列其他的结构就不需要修改了。

typedef struct QueueNode
{
	struct QueueNode* next;
	QDataType val;
} QNode;

typedef struct Queue
{
	QNode* phead;
	QNode* ptail;
	int size;
} Queue;

1.2 关键接口实现

层序遍历依赖以下核心接口：

• QueuePush：将节点指针入队。
• QueuePop：将队头元素出队。
• QueueFront：获取当前待处理的节点。
• QueueEmpty：判断当前层是否处理完毕。

这里就不给出代码了，因为不是重点，可以看一下手撕队列（Queue）这篇文章。

---

二、层序遍历的算法逻辑

层序遍历的核心思想是："在队列中出一个节点，带入它的左右孩子"。

2.1 算法流程

1. 将根节点入队。
2. 只要队列不为空，执行循环：
   • 提取队头节点 front 并将其出队。
   • 访问该节点（例如打印其数据）。
   • 若左孩子存在，左孩子入队。
   • 若右孩子存在，右孩子入队。

2.2 代码实现

void TreeLevelOrder(BTNode* root)
{
	Queue q;            // 声明一个队列
	QueueInit(&q);      // 初始化队列，将头尾指针置空，size置0

	// 如果根节点不为空，则将根节点入队
	if (root)
		QueuePush(&q, root);

	// 只要队列不为空，就继续遍历
	while (!QueueEmpty(&q))
	{
		// 1. 获取当前队头存储的二叉树节点
		BTNode* front = QueueFront(&q);
		
		// 2. 将该节点从队列中弹出
		QueuePop(&q);

		// 3. 访问该节点（此处为打印节点存储的数据）
		printf("%d ", front->data);
		
		// 4. 关键逻辑：按照"左孩子先入，右孩子后入"的原则
		// 这样在下一层遍历时，依然能保持从左到右的顺序
		if (front->left)
			QueuePush(&q, front->left);  // 若左子树非空，入队
		if (front->right)
			QueuePush(&q, front->right); // 若右子树非空，入队
	}

	// 遍历结束，销毁队列释放内存
	QueueDestroy(&q);
}

---

三、核心进阶------判定完全二叉树

完全二叉树（Complete Binary Tree）要求：除了最后一层外，其他各层节点全满，且最后一层的节点必须连续集中在左侧。这时候就有这么几种情况：

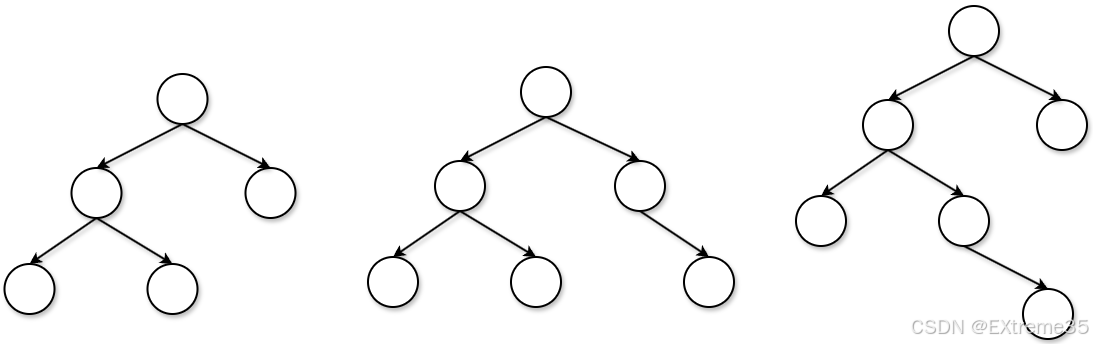
3.1 洞察：完全二叉树的"连续性"

完全二叉树的定义要求：除了最后一层外，其他各层节点全满，且最后一层的节点必须连续集中在左侧。

• 如果我们进行层序遍历，并允许将空节点（NULL）也推入队列 ，你会发现：
  • 完全二叉树 ：在遍历序列中，所有的非空节点一定是连续的。一旦遇到第一个 NULL，后面应该全是 NULL。
  • 非完全二叉树 ：在遇到第一个 NULL 之后，序列中还会出现非空节点（即"空隙"）。

3.2 那些"看似可行"但不适合的经典思路

在判断完全二叉树时，初学者常会尝试用一些简单的属性（如树高、节点数）来推导，但这些思路往往存在逻辑漏洞。

避坑思路一：仅通过"节点总数"判断

• 思路描述 ：计算树的高度 h h h 和总节点数 n n n。如果 2 h − 1 ≤ n ≤ 2 h − 1 2^{h-1} \le n \le 2^h - 1 2h−1≤n≤2h−1，则判定为完全二叉树。
• 为何不适合 ：这个范围是完全二叉树的必要条件 ，但不是充分条件 。例如上图第二个
  • 反例 ：一棵树高度为 3，节点总数为 4。虽然满足 4 ≤ 4 ≤ 7 4 \le 4 \le 7 4≤4≤7，但如果这 4 个节点全部偏向右侧（例如根节点的左子树为空），它依然不是完全二叉树。单靠数量无法限制节点的"左对齐"特性。

避坑思路二：仅比较左右子树的高度差

• 思路描述：认为完全二叉树左右子树高度差绝对值不超过 1。
• 为何不适合 ：这混淆了"平衡二叉树"和"完全二叉树"的概念。
  • 反例：即使左右子树高度差为 0（如满二叉树缺少了倒数第二层的某个中间节点），只要最后一层的节点不连续，它就不是完全二叉树。

3.3 判定的绝妙思路

在层序遍历时，如果我们不论节点是否为空（NULL）都将其推入队列，完全二叉树会呈现出一种独特的性质：

• 完全二叉树 ：所有非空节点在队列中是连续的，一旦遇到 NULL，之后队列中剩下的必须全部是 NULL。
• 非完全二叉树 ：在遇到第一个 NULL 后，队列中后续还会出现非空节点。

那有的人就会觉得这个思路也不完整，万一出现上图第三个那种情况呢？

这么思考一下，最下层孩子节点在其父亲节点出队的时候，就已经入队了，而下一个节点为空，此时队列不空，所以不是完全二叉树。

就算你在最下层节点再加孩子节点也一样，因为只要第一个是空，后续必须全空，只要队列有一个元素，那也就能直接判断了。

判定代码实现

该算法分为两个阶段：第一阶段寻找第一个 NULL；第二阶段检查 NULL 之后是否还有有效节点。

bool TreeComplete(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	if (root)
		QueuePush(&q, root);

	// 第一阶段：层序遍历，直到遇到第一个 NULL 节点
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);

		if (front == NULL)
		{
			break; // 遇到第一个空，进入第二阶段校验
		}
		// 无论左右子节点是否为空，统一入队
		QueuePush(&q, front->left);
		QueuePush(&q, front->right);
	}

	// 第二阶段：检查队列中剩余的元素
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);

		// 如果在 NULL 之后又发现了有效节点，则不是完全二叉树
		if (front)
		{
			QueueDestroy(&q);
			return false;
		}
	}

	QueueDestroy(&q);
	return true;
}

---

四、总结与复杂度分析

4.1 复杂度

• 时间复杂度 ： O ( N ) O(N) O(N)。树中的每个节点（包括完全二叉树判定中的 NULL 节点边界）都会入队和出队一次。
• 空间复杂度 ： O ( N ) O(N) O(N)。队列中最极端的情况下会存储树中一层的所有节点，对于满二叉树而言，最底层节点约为 N / 2 N/2 N/2。

4.2 核心要点

1. 队列的选择：必须使用能存储指针的队列，这样才能通过队列找到二叉树的子节点。
2. 内存管理 ：在 C 语言中，动态开辟的队列节点（QNode）必须在遍历结束后通过 QueueDestroy 彻底释放，防止内存泄漏。
3. NULL 的妙用 ：在判定完全二叉树时，将 NULL 入队是区分"连续性"的关键技巧。

通过以上代码与逻辑的结合，我们不仅掌握了如何"看"一棵树，更学会了如何通过逻辑规则去"审视"一棵树的形态。