【算法基础篇】（三十七）图论基础之单源最短路：从原理到实战，4 大算法彻底吃透！

前言

在图论的世界里，"最短路径" 绝对是最核心、最实用的问题之一。想象一下：外卖骑手规划最优配送路线、导航软件计算两地最短车程、网络数据寻找最快传输路径...... 这些场景的背后，都离不开单源最短路算法的支撑。

单源最短路，顾名思义，就是从图中的一个固定起点出发，找到通往其他所有顶点的最短路径（这里的 "最短" 可以是距离、时间、成本等带权指标）。看似简单的问题，在不同的图结构（有无负权边、有无负环）下，却有着截然不同的解决方案。

今天这篇文章，我会从基础概念入手，循序渐进地讲解 4 种经典的单源最短路算法 ------Dijkstra（常规版 + 堆优化版）、Bellman-Ford、SPFA，不仅会剖析每种算法的核心思想、适用场景，还会附上完整的 C++ 代码实现和洛谷实战例题，帮你从 "理解" 到 "会用"，彻底搞定单源最短路问题！

一、前置知识：搞懂这些概念，算法学习不迷路

在正式讲解算法之前，我们先梳理几个必须掌握的基础概念，避免后续理解出现偏差：

1. 什么是 "带权路径长度"？

在带权图中，从顶点vi到顶点vj的路径上，所有边的权值之和，就是这条路径的带权路径长度。而我们要找的 "最短路径"，就是带权路径长度最小的那条（如果存在多条路径的话）。

2. 单源最短路的核心场景分类

根据图的边权特性，单源最短路问题主要分为以下 3 种场景：

场景 1：图中所有边的权值都是非负数（最常见场景，如道路距离、传输延迟）；

场景 2：图中存在负权边，但没有负环（如带有 "优惠""返利" 的成本计算）；

场景 3：图中存在负环（此时可能不存在最短路径，因为可以无限绕负环减小路径长度）。

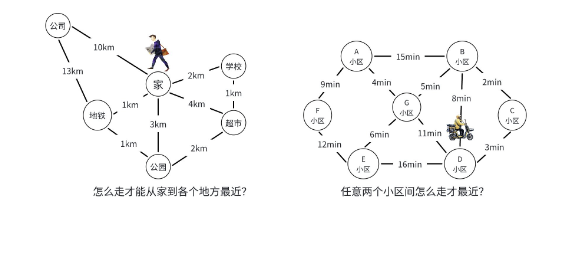
不同场景对应不同的算法，这也是我们选择算法的核心依据，后面会详细说明。

3. 关键定义：负环是什么？

负环（negative cycle） 是指一条边权之和为负数 的回路。例如，顶点A→B→C→A的边权之和为-5，这就是一个负环。

如果起点能到达负环，那么从起点到负环上的顶点就不存在最短路径 ------ 因为可以无限次绕负环，每次绕圈都会让路径长度减小，趋于负无穷。这一点在后续算法中会重点处理。

4. 松弛操作：所有最短路算法的核心

"松弛"（Relaxation）是最短路算法的核心操作，本质是 "寻找更短路径" 的过程。我们用dist[u] 表示从起点到顶点u的当前最短路径长度 ，对于边u→v（权值为w），如果满足：

cpp 复制代码

dist[v] > dist[u] + w

说明我们找到了一条从起点到v的更短路径（经过u到达v），此时就需要更新dist[v] = dist[u] + w。这个过程就叫做 "松弛"------ 可以理解为把v到起点的 "距离上限" 不断收紧，直到达到真正的最短距离。

所有单源最短路算法，本质上都是在不断进行松弛操作，只是松弛的顺序和策略不同。

二、Dijkstra 算法：非负权图的最优解

Dijkstra 算法是荷兰计算机科学家 Edsger W. Dijkstra 在 1956 年提出的，专门用于解决非负权图的单源最短路问题。算法基于 "贪心思想"，核心逻辑是：每次选择当前距离起点最近的未确定最短路径的顶点，确定其最短路径，然后以该顶点为中介，松弛其邻接顶点的距离。

1. 常规版 Dijkstra：适合稠密图

核心思想

初始化：创建dist数组（存储起点到各顶点的最短距离），dist[起点] = 0，其余顶点的dist值设为无穷大（表示暂时未找到路径）；创建st数组（标记顶点是否已确定最短路径），初始全为false。

迭代过程（共迭代n-1次，n为顶点数）：

在所有未确定最短路径的顶点中（st[u] = false），找到**dist[u]**最小的顶点u；

标记u为已确定最短路径（st[u] = true）；

以u为中介，对所有与u相邻的顶点v进行松弛操作：如果dist[v] > dist[u] + w(u→v)，则更新dist[v]。

结束：dist数组中存储的就是起点到各顶点的最短距离。

为什么能这么做？

因为图中所有边的权值都是非负数，一旦某个顶点被标记为 "已确定最短路径"（加入st数组），就意味着再也找不到比当前dist值更短的路径了 ------ 后续的松弛操作只会基于更长或相等的路径，无法更新该顶点的dist值。这就是贪心思想的合理性基础。

C++ 代码实现（邻接表版本）

python 复制代码

#include <iostream>
#include <vector>
#include <climits>
using namespace std;

typedef pair<int, int> PII;  // first: 邻接顶点，second: 边权
const int N = 1e4 + 10;
const int INF = INT_MAX;

int n, m, s;  // n: 顶点数，m: 边数，s: 起点
vector<PII> edges[N];  // 邻接表存储图
long long dist[N];     // 存储最短距离（用long long避免溢出）
bool st[N];            // 标记是否已确定最短路径

void dijkstra() {
    // 初始化dist数组
    for (int i = 1; i <= n; ++i) {
        dist[i] = INF;
    }
    dist[s] = 0;

    // 迭代n-1次（最多需要确定n-1个顶点的最短路径）
    for (int i = 1; i < n; ++i) {
        // 步骤1：找到当前未确定最短路径且dist最小的顶点u
        int u = 0;
        for (int j = 1; j <= n; ++j) {
            if (!st[j] && (u == 0 || dist[j] < dist[u])) {
                u = j;
            }
        }

        // 步骤2：标记u为已确定最短路径
        st[u] = true;

        // 步骤3：松弛u的所有邻接边
        for (auto& t : edges[u]) {
            int v = t.first;
            int w = t.second;
            if (dist[u] != INF && dist[v] > dist[u] + w) {
                dist[v] = dist[u] + w;
            }
        }
    }

    // 输出结果
    for (int i = 1; i <= n; ++i) {
        if (dist[i] == INF) {
            cout << INT_MAX << " ";  // 无法到达
        } else {
            cout << dist[i] << " ";
        }
    }
}

int main() {
    cin >> n >> m >> s;
    for (int i = 0; i < m; ++i) {
        int u, v, w;
        cin >> u >> v >> w;
        edges[u].push_back({v, w});  // 有向边
    }

    dijkstra();
    return 0;
}

时间复杂度分析

外层循环：n-1次迭代；

内层找最小dist的顶点：每次O(n)；

松弛操作：总共**O(m)**（因为每个边只会被遍历一次）。

总体时间复杂度为**O(n² + m)** 。对于稠密图 （边数m ≈ n²），这个复杂度是可接受的，但对于稀疏图 （边数m ≈ n），O(n²)的时间会非常低效 ------ 这就需要堆优化版的 Dijkstra 算法。

2. 堆优化版 Dijkstra：稀疏图的救星

核心优化点

常规版 Dijkstra 的瓶颈在于**"每次找最小dist的顶点"** 需要**O(n)** 时间。我们可以用优先级队列（小根堆） 来维护未确定最短路径的顶点，这样每次取最小dist的顶点只需要**O(log n)**时间，从而大幅降低时间复杂度。

算法流程

初始化：dist数组仍设为无穷大，dist[s] = 0；st数组初始全为false；创建小根堆，将(0, s)（第一个元素是dist值，第二个是顶点编号）入堆。

迭代过程（堆不为空）：

弹出堆顶元素(dist_u, u)（即当前dist最小的顶点）；

如果u已确定最短路径（st[u] = true），直接跳过（因为堆中可能存在旧的、非最优的dist值）；

标记u为已确定最短路径（st[u] = true）；

松弛u的所有邻接边：如果dist[v] > dist[u] + w，更新dist[v]，并将(dist[v], v)入堆。

结束：dist数组即为所求。

为什么堆中会有重复元素？

因为当某个顶点v的dist值被更新后，之前入堆的旧dist值还存在。但由于小根堆的特性，新的、更小的dist值会先被弹出处理，当旧值被弹出时，v已经被标记为st[v] = true，直接跳过即可，不影响结果。

C++ 代码实现（邻接表版本）

cpp 复制代码

#include <iostream>
#include <vector>
#include <queue>
#include <cstring>
using namespace std;

typedef pair<int, int> PII;  // first: dist值，second: 顶点编号
const int N = 1e5 + 10;
const int INF = 0x3f3f3f3f;  // 常用无穷大表示

int n, m, s;
vector<PII> edges[N];
int dist[N];
bool st[N];

void dijkstra() {
    // 初始化dist数组
    memset(dist, 0x3f, sizeof dist);
    dist[s] = 0;

    // 小根堆：按dist值从小到大排序
    priority_queue<PII, vector<PII>, greater<PII>> heap;
    heap.push({0, s});

    while (!heap.empty()) {
        // 弹出当前dist最小的顶点
        auto t = heap.top();
        heap.pop();
        int u = t.second;
        int dist_u = t.first;

        // 跳过已确定最短路径的顶点
        if (st[u]) continue;
        st[u] = true;

        // 松弛邻接边
        for (auto& edge : edges[u]) {
            int v = edge.first;
            int w = edge.second;
            if (dist[v] > dist_u + w) {
                dist[v] = dist_u + w;
                heap.push({dist[v], v});
            }
        }
    }

    // 输出结果
    for (int i = 1; i <= n; ++i) {
        cout << dist[i] << " ";
    }
}

int main() {
    cin >> n >> m >> s;
    for (int i = 0; i < m; ++i) {
        int u, v, w;
        cin >> u >> v >> w;
        edges[u].push_back({v, w});
    }

    dijkstra();
    return 0;
}

时间复杂度分析

堆操作 ：每个边最多会导致一次入堆操作，堆的插入和弹出时间都是O(log n)，因此堆操作的总时间是**O(m log n)**；

松弛操作 ：每个边只会被处理一次，O(m)。

总体时间复杂度为**O(m log n)** ，这对于稀疏图（m ≈ n）来说，比常规版的**O(n²)**高效得多，是实际应用中最常用的单源最短路算法。

注意事项

堆优化版 Dijkstra 同样只适用于非负权图！如果图中存在负权边，可能会导致顶点被多次入堆，甚至陷入死循环，最终无法得到正确结果。

3. 洛谷实战：单源最短路模板题

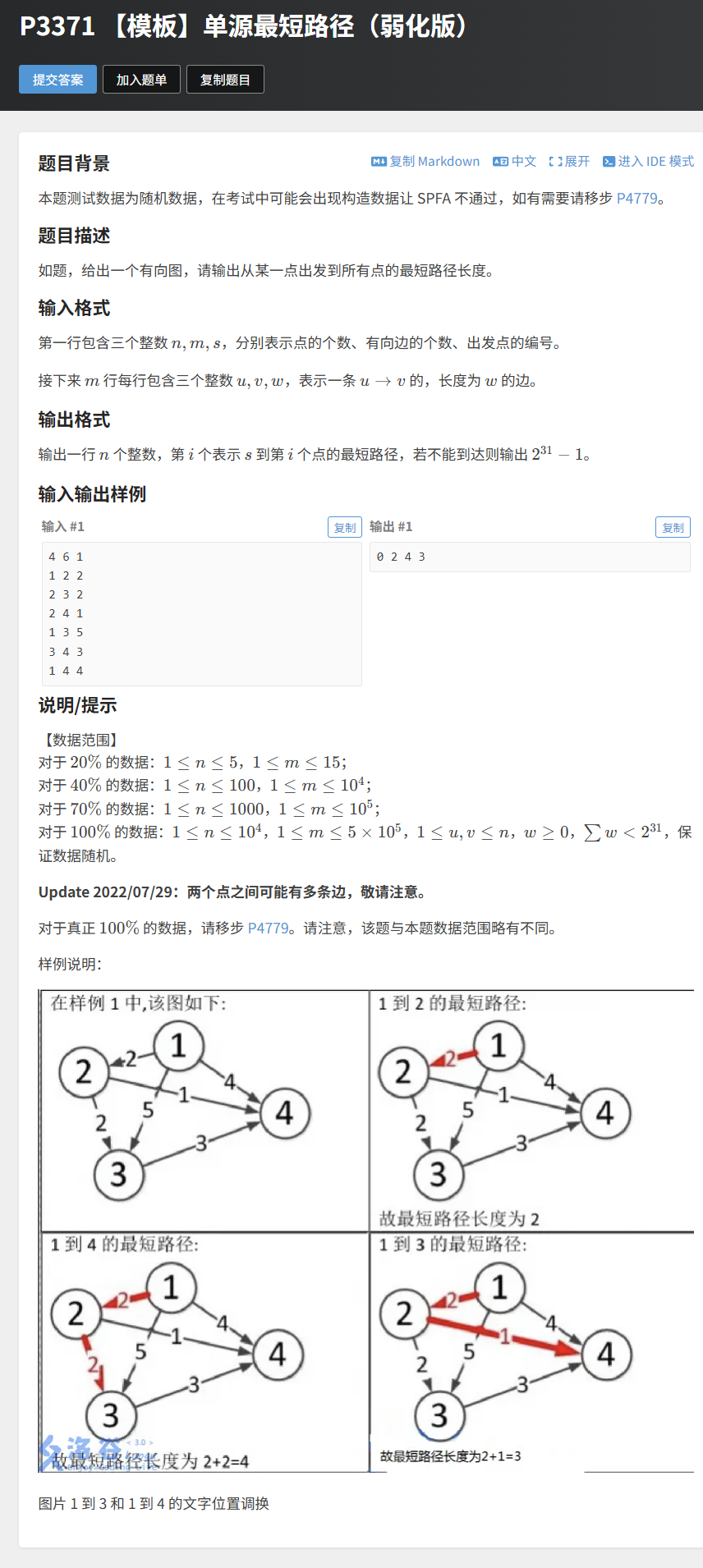
题目链接：P3371 【模板】单源最短路径（弱化版）

https://www.luogu.com.cn/problem/P3371

难度：★★
题意：给出有向图，输出从起点到所有顶点的最短路径长度，无法到达则输出2^31 - 1。
数据范围：n ≤ 1e4，m ≤ 5e4（适合常规版 Dijkstra）。

参考代码（直接复用常规版 Dijkstra）

cpp 复制代码

#include <iostream>
#include <vector>
#include <climits>
using namespace std;

typedef pair<int, int> PII;
const int N = 1e4 + 10;
const int INF = INT_MAX;

int n, m, s;
vector<PII> edges[N];
long long dist[N];
bool st[N];

void dijkstra() {
    for (int i = 1; i <= n; ++i) dist[i] = INF;
    dist[s] = 0;

    for (int i = 1; i < n; ++i) {
        int u = 0;
        for (int j = 1; j <= n; ++j) {
            if (!st[j] && (u == 0 || dist[j] < dist[u])) u = j;
        }

        st[u] = true;

        for (auto& t : edges[u]) {
            int v = t.first, w = t.second;
            if (dist[u] != INF && dist[v] > dist[u] + w) {
                dist[v] = dist[u] + w;
            }
        }
    }

    for (int i = 1; i <= n; ++i) {
        cout << (dist[i] == INF ? INF : dist[i]) << " ";
    }
}

int main() {
    cin >> n >> m >> s;
    for (int i = 0; i < m; ++i) {
        int u, v, w;
        cin >> u >> v >> w;
        edges[u].push_back({v, w});
    }

    dijkstra();
    return 0;
}

题目链接：P4779 【模板】单源最短路径（标准版）

https://www.luogu.com.cn/problem/P4779

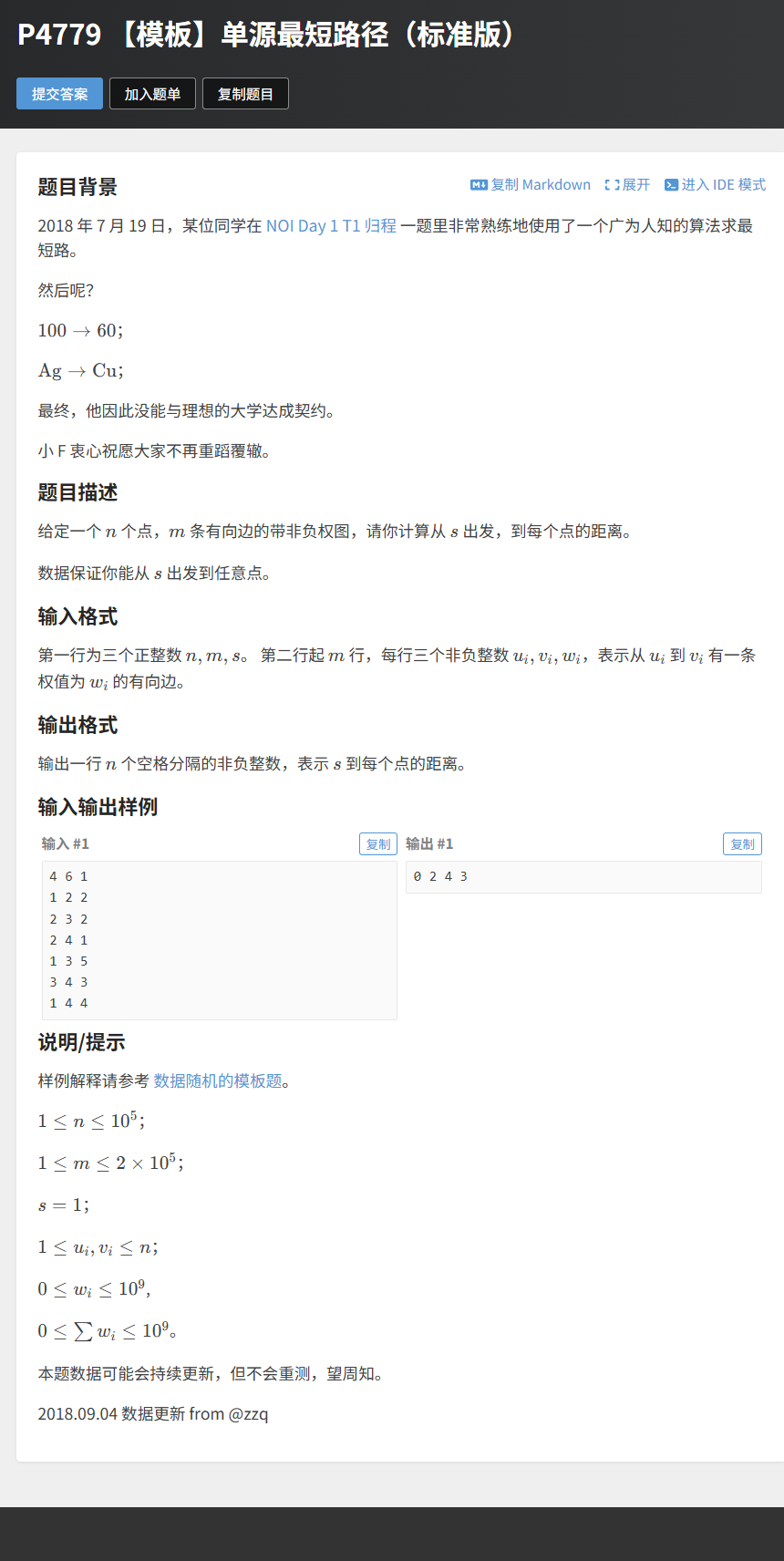
难度：★★
题意：与弱化版一致，但数据范围更大（n ≤ 1e5，m ≤ 2e5），必须用堆优化版 Dijkstra。

参考代码（复用堆优化版 Dijkstra）

cpp 复制代码

#include <iostream>
#include <vector>
#include <queue>
#include <cstring>
using namespace std;

typedef pair<int, int> PII;
const int N = 1e5 + 10;
const int INF = 0x3f3f3f3f;

int n, m, s;
vector<PII> edges[N];
int dist[N];
bool st[N];

void dijkstra() {
    memset(dist, 0x3f, sizeof dist);
    dist[s] = 0;

    priority_queue<PII, vector<PII>, greater<PII>> heap;
    heap.push({0, s});

    while (!heap.empty()) {
        auto t = heap.top();
        heap.pop();
        int u = t.second, dist_u = t.first;

        if (st[u]) continue;
        st[u] = true;

        for (auto& edge : edges[u]) {
            int v = edge.first, w = edge.second;
            if (dist[v] > dist_u + w) {
                dist[v] = dist_u + w;
                heap.push({dist[v], v});
            }
        }
    }

    for (int i = 1; i <= n; ++i) {
        cout << dist[i] << " ";
    }
}

int main() {
    cin >> n >> m >> s;
    for (int i = 0; i < m; ++i) {
        int u, v, w;
        cin >> u >> v >> w;
        edges[u].push_back({v, w});
    }

    dijkstra();
    return 0;
}

三、Bellman-Ford 算法：处理负权边的 "暴力美学"

Dijkstra 算法虽然高效，但无法处理负权边 ------ 一旦出现负权边，其 "标记顶点为已确定最短路径" 的贪心策略就会失效。而 Bellman-Ford 算法则不同，它通过**"暴力松弛所有边"** 的方式，不仅能处理负权边，还能判断图中是否存在负环。

1. 核心思想

Bellman-Ford 算法的核心是 "重复松弛所有边"，直到没有边可以被松弛为止。其理论依据是：在一个有n个顶点的图中，最短路径最多包含n-1条边（如果包含n条边，说明存在回路，而回路的权值之和非负时可以去掉，负权回路则不存在最短路径）。因此，最多需要进行n-1轮松弛操作，就能得到所有顶点的最短路径。

算法流程

初始化 ：dist数组设为无穷大，dist[s] = 0；

迭代过程 （共n-1轮）：

每一轮遍历所有边u→v（权值w）；

对每条边进行松弛操作：如果dist[v] > dist[u] + w，则更新dist[v]；

优化：如果某一轮没有任何边被松弛，说明所有最短路径已经确定，可以提前退出；

负环判断 ：进行第n轮松弛操作，如果仍有边可以被松弛，说明图中存在负环（因为n-1轮后已经应该得到最短路径，第n轮还能松弛说明存在可以无限缩短路径的负环）。

为什么能处理负权边？

因为 Bellman-Ford 算法没有 "标记已确定最短路径" 的步骤，即使某个顶点的dist值已经很小，后续仍可能通过负权边更新它。这种 "不设限" 的松弛策略，使得它能适应负权边的场景。

2. C++ 代码实现

cpp 复制代码

#include <iostream>
#include <vector>
#include <climits>
using namespace std;

typedef pair<int, int> PII;
const int N = 1e4 + 10;
const int INF = INT_MAX;

int n, m, s;
vector<PII> edges[N];  // edges[u]存储(u的邻接顶点v, 边权w)
int dist[N];

void bellman_ford() {
    // 初始化dist数组
    for (int i = 1; i <= n; ++i) {
        dist[i] = INF;
    }
    dist[s] = 0;

    // 进行n-1轮松弛
    for (int i = 1; i < n; ++i) {
        bool flag = false;  // 标记本轮是否有边被松弛
        for (int u = 1; u <= n; ++u) {
            if (dist[u] == INF) continue;  // u不可达，跳过
            for (auto& t : edges[u]) {
                int v = t.first;
                int w = t.second;
                if (dist[v] > dist[u] + w) {
                    dist[v] = dist[u] + w;
                    flag = true;
                }
            }
        }
        if (!flag) break;  // 没有边被松弛，提前退出
    }

    // 负环判断（可选）
    bool has_negative_cycle = false;
    for (int u = 1; u <= n; ++u) {
        if (dist[u] == INF) continue;
        for (auto& t : edges[u]) {
            int v = t.first;
            int w = t.second;
            if (dist[v] > dist[u] + w) {
                has_negative_cycle = true;
                break;
            }
        }
        if (has_negative_cycle) break;
    }

    // 输出结果
    if (has_negative_cycle) {
        cout << "图中存在负环，部分顶点无最短路径" << endl;
    } else {
        for (int i = 1; i <= n; ++i) {
            cout << (dist[i] == INF ? INF : dist[i]) << " ";
        }
    }
}

int main() {
    cin >> n >> m >> s;
    for (int i = 0; i < m; ++i) {
        int u, v, w;
        cin >> u >> v >> w;
        edges[u].push_back({v, w});
    }

    bellman_ford();
    return 0;
}

3. 时间复杂度分析

外层循环 ：n-1轮；

内层循环 ：每轮遍历所有m条边。

总体时间复杂度为**O(nm)** 。这个复杂度在n和m较大时（如n=1e4，m=1e5）会非常低效，因此 Bellman-Ford 算法通常用于处理小规模图 或需要判断负环的场景。

4. 洛谷实战：采购特价商品

题目链接：P1744 采购特价商品

https://www.luogu.com.cn/problem/P1744

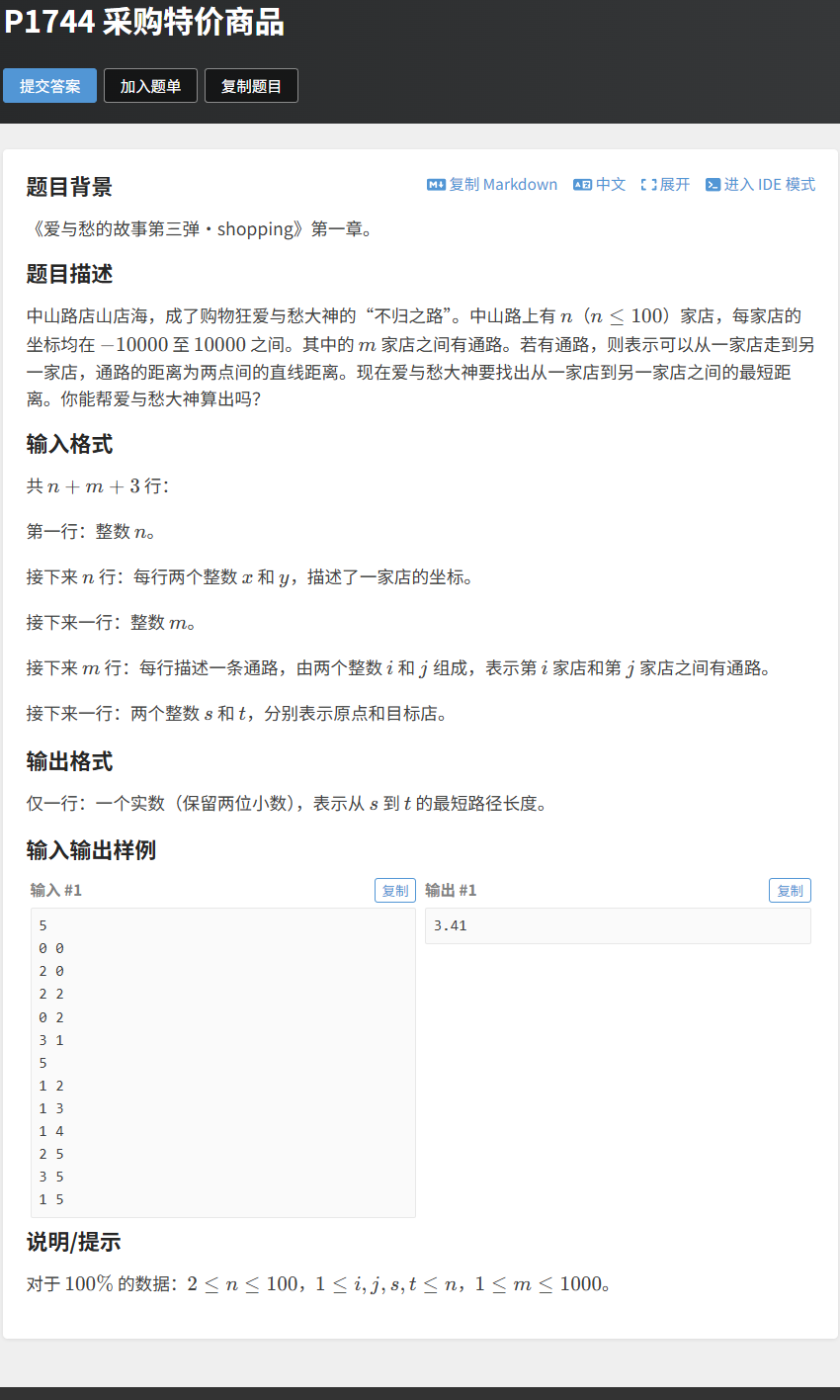
难度：★★
题意：给出n家店的坐标，m条通路（无向边），通路的距离为两点间的直线距离。求从起点s到终点t的最短路径长度（保留两位小数）。
思路：这是一个无向带权图，边权为直线距离（非负），但数据范围较小（n ≤ 100），适合用 Bellman-Ford 算法实现。

参考代码

cpp 复制代码

#include <iostream>
#include <cmath>
#include <cstring>
using namespace std;

const int N = 110, M = 1010;
const double INF = 1e10;

int n, m, s, t;
double x[N], y[N];  // 每家店的坐标

// 存储边：a和b是店的编号，c是边权（直线距离）
struct Edge {
    int a, b;
    double c;
} edges[M];

double dist[N];

// 计算两点间的直线距离
double calc(int i, int j) {
    double dx = x[i] - x[j];
    double dy = y[i] - y[j];
    return sqrt(dx * dx + dy * dy);
}

void bellman_ford() {
    // 初始化dist数组
    for (int i = 1; i <= n; ++i) {
        dist[i] = INF;
    }
    dist[s] = 0;

    // 进行n-1轮松弛
    for (int i = 1; i < n; ++i) {
        bool flag = false;
        for (int j = 1; j <= m; ++j) {
            int a = edges[j].a;
            int b = edges[j].b;
            double c = edges[j].c;
            // 无向边，双向松弛
            if (dist[a] + c < dist[b]) {
                dist[b] = dist[a] + c;
                flag = true;
            }
            if (dist[b] + c < dist[a]) {
                dist[a] = dist[b] + c;
                flag = true;
            }
        }
        if (!flag) break;
    }

    // 输出结果（保留两位小数）
    printf("%.2lf\n", dist[t]);
}

int main() {
    cin >> n;
    for (int i = 1; i <= n; ++i) {
        cin >> x[i] >> y[i];
    }
    cin >> m;
    for (int i = 1; i <= m; ++i) {
        int a, b;
        cin >> a >> b;
        edges[i].a = a;
        edges[i].b = b;
        edges[i].c = calc(a, b);
    }
    cin >> s >> t;

    bellman_ford();
    return 0;
}

四、SPFA 算法：Bellman-Ford 的 "智能优化版"

Bellman-Ford 算法的**O(nm)** 复杂度实在太高，而我们观察到：只有上一轮被松弛过的顶点，其邻接边才有可能在当前轮松弛其他顶点。基于这个观察，我们可以用队列来维护 "待松弛的顶点"，从而减少不必要的松弛操作 ------ 这就是 SPFA 算法（Shortest Path Faster Algorithm）。

1. 核心思想

SPFA 算法本质是 Bellman-Ford 算法的队列优化，核心优化点：

用队列存储需要进行松弛操作的顶点；

只有当顶点u的dist值被更新后，才将其入队（如果不在队列中）；

每次从队列中取出顶点u，对其邻接边进行松弛操作。

这种优化使得 SPFA 算法在大多数情况下的时间复杂度远低于**O(nm)** （实际约为O(km)，k是每个顶点入队的平均次数，通常k ≤ 2），成为处理有负权边但无负环的图的首选算法。

2. 算法流程

初始化 ：dist数组设为无穷大，dist[s] = 0；创建队列，将起点s入队；创建st数组（标记顶点是否在队列中），st[s] = true。

迭代过程 （队列不为空）：

取出队头顶点u，标记st[u] = false（表示已出队）；

遍历u的所有邻接边u→v（权值w）；

松弛操作：如果dist[v] > dist[u] + w，更新dist[v]；

如果v不在队列中（st[v] = false），将v入队，标记st[v] = true。

负环判断 （可选）：创建cnt数组，记录每个顶点的入队次数。如果某个顶点v的入队次数cnt[v] ≥ n，说明存在负环（因为最短路径最多包含n-1条边，入队n次意味着绕了至少一次环，且是负环）。

3. C++ 代码实现

cpp 复制代码

#include <iostream>
#include <vector>
#include <queue>
#include <climits>
using namespace std;

typedef pair<int, int> PII;
const int N = 1e4 + 10;
const int INF = INT_MAX;

int n, m, s;
vector<PII> edges[N];
int dist[N];
bool st[N];  // 标记是否在队列中
int cnt[N];  // 记录入队次数（用于负环判断）

bool spfa() {
    // 初始化
    for (int i = 1; i <= n; ++i) {
        dist[i] = INF;
        st[i] = false;
        cnt[i] = 0;
    }
    dist[s] = 0;
    queue<int> q;
    q.push(s);
    st[s] = true;
    cnt[s] = 1;

    while (!q.empty()) {
        int u = q.front();
        q.pop();
        st[u] = false;

        // 松弛邻接边
        for (auto& t : edges[u]) {
            int v = t.first;
            int w = t.second;
            if (dist[u] != INF && dist[v] > dist[u] + w) {
                dist[v] = dist[u] + w;
                if (!st[v]) {
                    q.push(v);
                    st[v] = true;
                    cnt[v]++;
                    // 入队次数≥n，存在负环
                    if (cnt[v] >= n) {
                        return true;
                    }
                }
            }
        }
    }

    return false;  // 无负环
}

int main() {
    cin >> n >> m >> s;
    for (int i = 0; i < m; ++i) {
        int u, v, w;
        cin >> u >> v >> w;
        edges[u].push_back({v, w});
    }

    bool has_negative_cycle = spfa();

    if (has_negative_cycle) {
        cout << "图中存在负环，部分顶点无最短路径" << endl;
    } else {
        for (int i = 1; i <= n; ++i) {
            cout << (dist[i] == INF ? INF : dist[i]) << " ";
        }
    }

    return 0;
}

4. 时间复杂度分析

平均情况 ：O(km) ，k通常是很小的常数（如 2~3）；

最坏情况 ：O(nm)（与 Bellman-Ford 相同，如存在负环时）。

5. 洛谷实战：负环模板题

题目链接：P3385 【模板】负环

https://www.luogu.com.cn/problem/P3385

难度：★★
题意：给定有向图，判断是否存在从顶点 1 出发能到达的负环。
思路：用 SPFA 算法的负环判断功能，通过cnt数组记录入队次数，若cnt[v] ≥ n则存在负环。

参考代码

cpp 复制代码

#include <iostream>
#include <vector>
#include <queue>
#include <cstring>
using namespace std;

typedef pair<int, int> PII;
const int N = 2e3 + 10;

int n, m;
vector<PII> edges[N];
int dist[N];
bool st[N];
int cnt[N];

bool spfa() {
    memset(dist, 0x3f, sizeof dist);
    memset(st, false, sizeof st);
    memset(cnt, 0, sizeof cnt);

    queue<int> q;
    q.push(1);
    dist[1] = 0;
    st[1] = true;
    cnt[1] = 1;

    while (!q.empty()) {
        int u = q.front();
        q.pop();
        st[u] = false;

        for (auto& t : edges[u]) {
            int v = t.first;
            int w = t.second;
            if (dist[v] > dist[u] + w) {
                dist[v] = dist[u] + w;
                if (!st[v]) {
                    q.push(v);
                    st[v] = true;
                    cnt[v]++;
                    if (cnt[v] >= n) {
                        return true;
                    }
                }
            }
        }
    }

    return false;
}

int main() {
    int T;
    cin >> T;
    while (T--) {
        cin >> n >> m;
        // 清空邻接表
        for (int i = 1; i <= n; ++i) {
            edges[i].clear();
        }
        for (int i = 0; i < m; ++i) {
            int u, v, w;
            cin >> u >> v >> w;
            edges[u].push_back({v, w});
            // 若w≥0，是无向边，添加反向边
            if (w >= 0) {
                edges[v].push_back({u, w});
            }
        }

        if (spfa()) {
            cout << "YES" << endl;
        } else {
            cout << "NO" << endl;
        }
    }

    return 0;
}

五、4 大算法横向对比：该选哪一个？

学到这里，你可能会疑惑：面对具体问题时，该如何选择合适的算法？下面这张表格，从核心特性、适用场景、时间复杂度等方面进行了全面对比，帮你快速决策：

算法	核心思想	负权边支持	负环检测	时间复杂度	适用场景
常规版 Dijkstra	贪心 + 松弛，标记已确定顶点	不支持	不支持	O(n² + m)	稠密图（非负权）
堆优化版 Dijkstra	小根堆优化找最小 dist 顶点	不支持	不支持	O(m log n)	稀疏图（非负权）、大规模图
Bellman-Ford	暴力松弛所有边 n-1 轮	支持	支持	O(nm)	小规模图、需要检测负环
SPFA	队列优化 Bellman-Ford	支持	支持	平均 O (km)，最坏 O (nm)	有负权边的图、需要检测负环

选择算法的 3 个步骤

先看图中是否有负权边 ：

无负权边：优先选堆优化版 Dijkstra（稀疏图）或常规版 Dijkstra（稠密图）；

有负权边：进入下一步；

再看是否需要检测负环 ：

需要检测负环：选 Bellman-Ford 或 SPFA；

确定无负环：选 SPFA（效率更高）；

结合数据规模 ：

数据规模大（n≥1e4，m≥1e5）：只能选堆优化版 Dijkstra 或 SPFA；

数据规模小（n≤1e3，m≤1e4）：可任选，Bellman-Ford 实现更简单。

六、进阶实战：单源最短路的经典变形问题

除了模板题，单源最短路还有很多经典变形问题，下面我们来看两个高频例题，帮你拓宽解题思路。

1. 例题 1：邮递员送信（往返最短路）

题目链接：P1629 邮递员送信

https://www.luogu.com.cn/problem/P1629

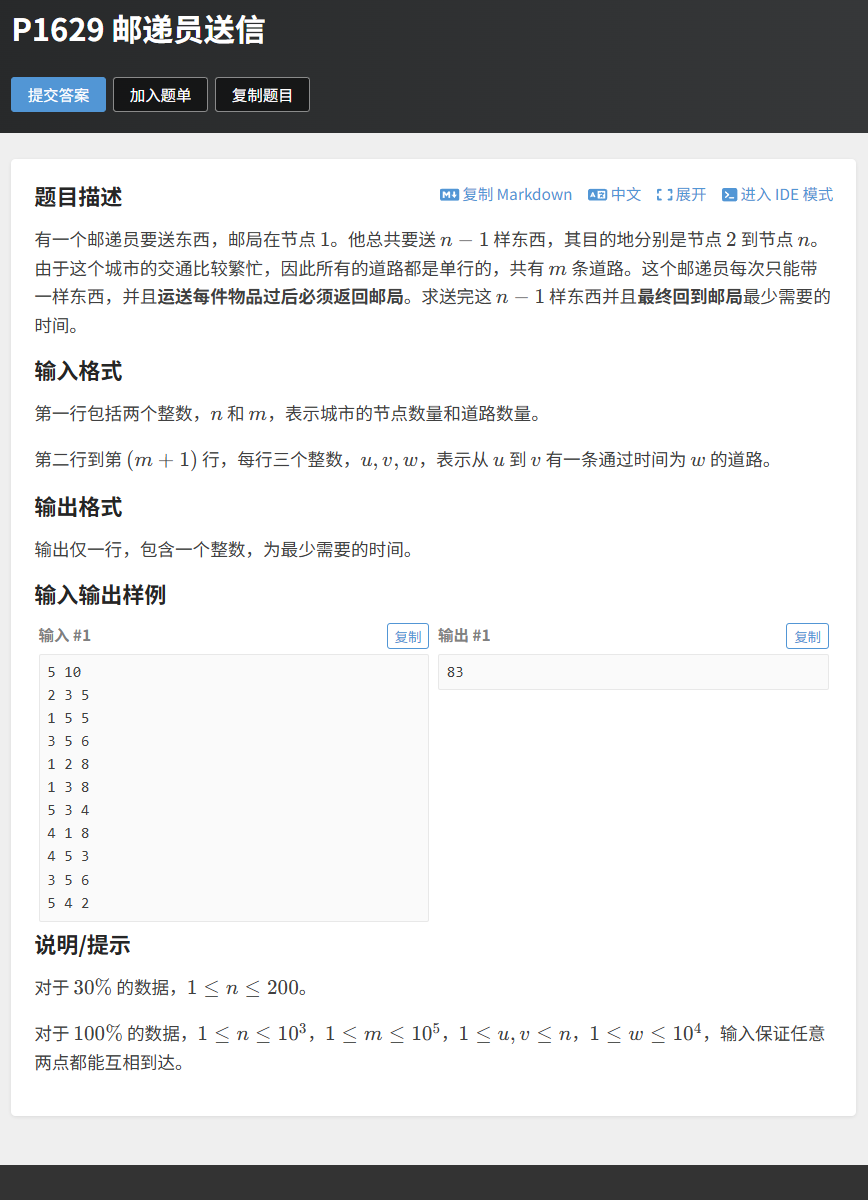
难度：★★
题意：有向图，邮递员从邮局（顶点 1）出发，送完所有目的地（顶点 2~n）后返回邮局，求最少需要的时间。
核心思路：
- 正向最短路：从顶点 1 到其他所有顶点的最短距离（送件路程）；
- 反向最短路：从其他所有顶点到顶点 1 的最短距离（返程路程）------ 这里可以通过 "建反图" 来实现：将原图中所有边的方向反转，然后求顶点 1 到其他所有顶点的最短距离，即为原图中其他顶点到顶点 1 的最短距离。
解法：用 Dijkstra 算法分别计算正向和反向最短路，求和即为答案。

参考代码

cpp 复制代码

#include <iostream>
#include <cstring>
using namespace std;

const int N = 1e3 + 10;
const int INF = 0x3f3f3f3f;

int n, m;
int g[N][N];  // 原图
int rev_g[N][N];  // 反图
int dist[N];
bool st[N];

// Dijkstra算法，graph为图，计算从s到所有顶点的最短距离
void dijkstra(int graph[][N]) {
    memset(dist, 0x3f, sizeof dist);
    memset(st, false, sizeof st);
    dist[1] = 0;

    for (int i = 1; i <= n; ++i) {
        // 找未确定最短路径且dist最小的顶点
        int u = 0;
        for (int j = 1; j <= n; ++j) {
            if (!st[j] && (u == 0 || dist[j] < dist[u])) {
                u = j;
            }
        }

        st[u] = true;

        // 松弛操作
        for (int v = 1; v <= n; ++v) {
            if (dist[v] > dist[u] + graph[u][v]) {
                dist[v] = dist[u] + graph[u][v];
            }
        }
    }
}

int main() {
    cin >> n >> m;

    // 初始化原图和反图
    memset(g, 0x3f, sizeof g);
    memset(rev_g, 0x3f, sizeof rev_g);
    for (int i = 1; i <= n; ++i) {
        g[i][i] = 0;
        rev_g[i][i] = 0;
    }

    for (int i = 0; i < m; ++i) {
        int u, v, w;
        cin >> u >> v >> w;
        g[u][v] = min(g[u][v], w);  // 原图：u→v
        rev_g[v][u] = min(rev_g[v][u], w);  // 反图：v→u（对应原图u→v）
    }

    // 计算正向最短路（送件）
    dijkstra(g);
    int res = 0;
    for (int i = 1; i <= n; ++i) {
        res += dist[i];
    }

    // 计算反向最短路（返程）
    dijkstra(rev_g);
    for (int i = 1; i <= n; ++i) {
        res += dist[i];
    }

    cout << res << endl;
    return 0;
}

2. 例题 2：最短路计数（统计最短路径条数）

题目链接：P1144 最短路计数

难度：★★★
题意：无向无权图，求从顶点 1 到其他每个顶点的最短路条数（答案对 100003 取模）。
核心思路：
- 由于是无权图，最短路长度就是边的条数，可以用 BFS 求解；
- 动态规划 ：设**f[v]**为从顶点 1 到v的最短路条数，**dist[v]**为最短路长度；
- 状态转移 ：当通过顶点u松弛到v时，若dist[v] == dist[u] + 1，则f[v] = (f[v] + f[u]) % MOD；若dist[v] > dist[u] + 1，则更新dist[v] = dist[u] + 1，f[v] = f[u]。
解法：BFS + 动态规划。

参考代码

cpp 复制代码

#include <iostream>
#include <queue>
#include <vector>
#include <cstring>
using namespace std;

const int N = 1e6 + 10;
const int MOD = 100003;
const int INF = 0x3f3f3f3f;

int n, m;
vector<int> edges[N];
int dist[N];
int f[N];  // f[v]：从1到v的最短路条数

void bfs() {
    memset(dist, 0x3f, sizeof dist);
    queue<int> q;

    dist[1] = 0;
    f[1] = 1;
    q.push(1);

    while (!q.empty()) {
        int u = q.front();
        q.pop();

        for (int v : edges[u]) {
            if (dist[v] > dist[u] + 1) {
                dist[v] = dist[u] + 1;
                f[v] = f[u];
                q.push(v);
            } else if (dist[v] == dist[u] + 1) {
                f[v] = (f[v] + f[u]) % MOD;
            }
        }
    }
}

int main() {
    scanf("%d%d", &n, &m);
    for (int i = 0; i < m; ++i) {
        int a, b;
        scanf("%d%d", &a, &b);
        edges[a].push_back(b);
        edges[b].push_back(a);
    }

    bfs();

    for (int i = 1; i <= n; ++i) {
        printf("%d\n", f[i]);
    }

    return 0;
}

总结

单源最短路是图论中的核心知识点，也是算法面试和竞赛中的高频考点。通过本文的学习，你应该已经掌握了 4 种经典算法的原理、实现和适用场景，以及常见的实战例题。

算法学习的关键在于 "理解 + 实践"，希望你能多动手敲代码，多做练习题，把这些算法真正内化为自己的技能。如果遇到问题，欢迎在评论区交流讨论！

【算法基础篇】（三十七）图论基础之单源最短路：从原理到实战，4 大算法彻底吃透！

目录

前言

一、前置知识：搞懂这些概念，算法学习不迷路

1. 什么是 "带权路径长度"？

2. 单源最短路的核心场景分类

3. 关键定义：负环是什么？

4. 松弛操作：所有最短路算法的核心

二、Dijkstra 算法：非负权图的最优解

1. 常规版 Dijkstra：适合稠密图

核心思想

为什么能这么做？

C++ 代码实现（邻接表版本）

时间复杂度分析

2. 堆优化版 Dijkstra：稀疏图的救星

核心优化点

算法流程

为什么堆中会有重复元素？

C++ 代码实现（邻接表版本）

时间复杂度分析

注意事项

3. 洛谷实战：单源最短路模板题

题目链接：P3371 【模板】单源最短路径（弱化版）

参考代码（直接复用常规版 Dijkstra）

题目链接：P4779 【模板】单源最短路径（标准版）

参考代码（复用堆优化版 Dijkstra）

三、Bellman-Ford 算法：处理负权边的 "暴力美学"

1. 核心思想

算法流程

为什么能处理负权边？

2. C++ 代码实现

3. 时间复杂度分析

4. 洛谷实战：采购特价商品

题目链接：P1744 采购特价商品

参考代码

四、SPFA 算法：Bellman-Ford 的 "智能优化版"

1. 核心思想

2. 算法流程

3. C++ 代码实现

4. 时间复杂度分析

5. 洛谷实战：负环模板题

题目链接：P3385 【模板】负环

参考代码

五、4 大算法横向对比：该选哪一个？

选择算法的 3 个步骤

六、进阶实战：单源最短路的经典变形问题

1. 例题 1：邮递员送信（往返最短路）

题目链接：P1629 邮递员送信

参考代码

2. 例题 2：最短路计数（统计最短路径条数）

题目链接：P1144 最短路计数

参考代码

总结