
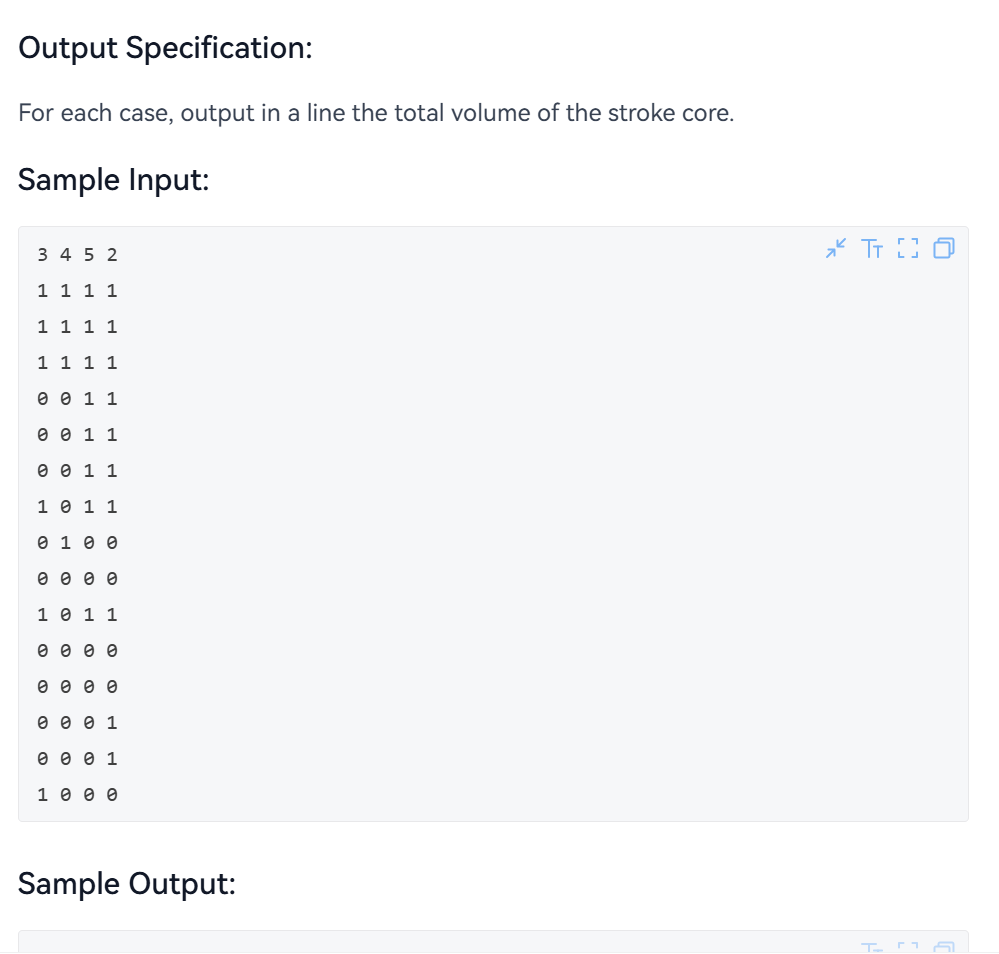
这一题的大意是说给出一个三维的矩阵,让我们找上下左右前后相互连通,面积大于等于T的数量,统计最终的面积。
看懂题目后实际上还是比较好写的。
我一开始无脑DFS搜索,找连通块
但写好代码后发现最后两个测试点段错误
DFS代码如下:
cpp
#include<bits/stdc++.h>
#include<iostream>
using namespace std;
int M;
int N;
int L;
//L是一个大脑中片的数量
int T;
//M,N是每一个片的大小面积
//最大是1286*128
//T是临界值,如果一个量连接核心是少于T那么这个核心一定不被数
//每一个玻片是由01构成 1代表stroke
// 0代表正常
// 因为玻片的厚度是不断的,我们仅仅不得不数1的数量去得到量
// 然后也许几个分开的核心区域在大脑中,并且仅仅这些量是不少于T
// 两个轴呗连接因此属于相同的区域,如果它们分享相同的方面
int t[80][1350][130];
int ans;
bool flag[80][1305][135];
void dfs(int x,int y,int z,int& cnt)
{
if(t[x][y][z]==1)
{
cnt++;
}
flag[x][y][z]=1;
if(x+1<L&&y<M&&z<N)
{
if(t[x+1][y][z]==1&&flag[x+1][y][z]==0)
{
dfs(x+1,y,z,cnt);
}
}
if(x<L&&y+1<M&&z<N)
{
if(t[x][y+1][z]==1&&flag[x][y+1][z]==0)
{
dfs(x,y+1,z,cnt);
}
}
if(x<L&&y<M&&z+1<N)
{
if(t[x][y][z+1]==1&&flag[x][y][z+1]==0)
{
dfs(x,y,z+1,cnt);
}
}
if(x-1>=0&&y<M&&z<N)
{
if(t[x-1][y][z]==1&&flag[x-1][y][z]==0)
{
dfs(x-1,y,z,cnt);
}
}
if(x<L&&y-1>=0&&z<N)
{
if(t[x][y-1][z]==1&&flag[x][y-1][z]==0)
{
dfs(x,y-1,z,cnt);
}
}
if(x<L&&y<M&&z-1>=0)
{
if(t[x][y][z-1]==1&&flag[x][y][z-1]==0)
{
dfs(x,y,z-1,cnt);
}
}
}
int main()
{
cin>>M>>N>>L>>T;
for(int i=0;i<L;i++)
{
for(int j=0;j<M;j++)
{
for(int k=0;k<N;k++)
{
int x;
cin>>x;
t[i][j][k]=x;
}
}
}
for(int i=0;i<L;i++)
{
for(int j=0;j<M;j++)
{
for(int k=0;k<N;k++)
{
if(t[i][j][k]==1&&flag[i][j][k]==0)
{
int cnt=0;
dfs(i,j,k,cnt);
if(cnt>=T)
{
ans+=cnt;
}
}
}
}
}
cout<<ans<<endl;
return 0;
}原因是数据范围过大,dfs递归栈无法开那么大,于是就段错误
因此这一题应该采用BFS,也就是用一个队列来保存
这样就不会递归爆栈了,思路很简单:
完整代码如下:
cpp
#include<bits/stdc++.h>
#include<iostream>
using namespace std;
int M;
int N;
int L;
//L是一个大脑中片的数量
int T;
//M,N是每一个片的大小面积
//最大是1286*128
//T是临界值,如果一个量连接核心是少于T那么这个核心一定不被数
//每一个玻片是由01构成 1代表stroke
// 0代表正常
// 因为玻片的厚度是不断的,我们仅仅不得不数1的数量去得到量
// 然后也许几个分开的核心区域在大脑中,并且仅仅这些量是不少于T
// 两个轴呗连接因此属于相同的区域,如果它们分享相同的方面
int t[80][1350][130];
int ans;
bool flag[80][1305][135];
void dfs(int x,int y,int z,int& cnt)
{
if(t[x][y][z]==1)
{
cnt++;
}
flag[x][y][z]=1;
if(x+1<L&&y<M&&z<N)
{
if(t[x+1][y][z]==1&&flag[x+1][y][z]==0)
{
dfs(x+1,y,z,cnt);
}
}
if(x<L&&y+1<M&&z<N)
{
if(t[x][y+1][z]==1&&flag[x][y+1][z]==0)
{
dfs(x,y+1,z,cnt);
}
}
if(x<L&&y<M&&z+1<N)
{
if(t[x][y][z+1]==1&&flag[x][y][z+1]==0)
{
dfs(x,y,z+1,cnt);
}
}
if(x-1>=0&&y<M&&z<N)
{
if(t[x-1][y][z]==1&&flag[x-1][y][z]==0)
{
dfs(x-1,y,z,cnt);
}
}
if(x<L&&y-1>=0&&z<N)
{
if(t[x][y-1][z]==1&&flag[x][y-1][z]==0)
{
dfs(x,y-1,z,cnt);
}
}
if(x<L&&y<M&&z-1>=0)
{
if(t[x][y][z-1]==1&&flag[x][y][z-1]==0)
{
dfs(x,y,z-1,cnt);
}
}
}
int main()
{
cin>>M>>N>>L>>T;
for(int i=0;i<L;i++)
{
for(int j=0;j<M;j++)
{
for(int k=0;k<N;k++)
{
int x;
cin>>x;
t[i][j][k]=x;
}
}
}
for(int i=0;i<L;i++)
{
for(int j=0;j<M;j++)
{
for(int k=0;k<N;k++)
{
if(t[i][j][k]==1&&flag[i][j][k]==0)
{
int cnt=0;
dfs(i,j,k,cnt);
if(cnt>=T)
{
ans+=cnt;
}
}
}
}
}
cout<<ans<<endl;
return 0;
}