PyTorch ExponentialLR：按指数学习率衰减原理、API、参数详解、实战

文章目录

[1、基本介绍 & API](#1、基本介绍 & API)
[2、解释 "指数"](#2、解释 “指数”)
[3、scheduler 属性 / 方法](#3、scheduler 属性 / 方法)
[4、代码 & 学习率趋势图 & 解释：](#4、代码 & 学习率趋势图 & 解释：)

1、基本介绍 & API

📉 "按指数学习率衰减"（Exponential Learning Rate Decay）

为什么叫 "指数"，详情在后面

✅ 核心思想

学习率不是"阶梯式"突变，而是每个 epoch 都乘以一个固定衰减因子 ，形成指数函数形式的连续衰减。

数学表达为：
η t = η 0 ⋅ γ t \eta_t = \eta_0 \cdot \gamma^t ηt=η0⋅γt

其中：

η 0 \eta_0 η0：初始学习率；
γ \gamma γ：衰减率（ 0 < γ < 1 0 < \gamma < 1 0<γ<1）；
t t t：当前 epoch 编号。

例如： γ = 0.95 \gamma = 0.95 γ=0.95 表示每轮学习率变为上一轮的 95%。

🔧 PyTorch API：ExponentialLR

构造函数

python 复制代码

torch.optim.lr_scheduler.ExponentialLR(optimizer, gamma, last_epoch=-1, verbose=False)

参数说明

参数	类型	说明
`optimizer`	`Optimizer`	绑定的优化器（必需）
`gamma`	`float`	关键参数：每轮衰减系数（如 `0.9`, `0.95`, `0.99`）
`last_epoch`	`int`	上一个 epoch 编号，用于恢复训练（默认 `-1`）
`verbose`	`bool`	是否打印学习率更新日志（PyTorch ≥1.9）

⚠️ 注意：gamma 必须满足 0 < gamma < 1。越接近 1，衰减越慢；越小，衰减越快。

🌰 举个例子

python 复制代码

optimizer = optim.SGD(model.parameters(), lr=0.1)
scheduler = ExponentialLR(optimizer, gamma=0.9)

学习率变化如下：

Epoch	学习率（近似）
0	0.1000
1	0.0900
2	0.0810
3	0.0729
10	0.0349
20	0.0122
50	0.0005

✅ 学习率每轮都在下降，但下降幅度逐渐变小（指数衰减特性）。

📈 可视化效果

与 StepLR 的"台阶"不同，ExponentialLR 的曲线是一条光滑的指数下降曲线：

复制代码

学习率
↑
│●
│ ●
│  ●
│   ●
│     ●
│        ●
│            ●
│                  ●
└────────────────────→ epoch

非常适合需要平滑、渐进式收敛的任务。

✅ 使用示例（完整代码）

python 复制代码

import torch
import torch.optim as optim
from torch.optim.lr_scheduler import ExponentialLR
import matplotlib.pyplot as plt

# 设置中文字体（可选）
import os
os.environ["KMP_DUPLICATE_LIB_OK"] = "TRUE"
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 虚拟参数
w = torch.tensor([0.0], requires_grad=True)
optimizer = optim.SGD([w], lr=0.1)

# 指数衰减：每轮乘以 0.95
scheduler = ExponentialLR(optimizer, gamma=0.95)

lr_list = []
epochs = 50

for epoch in range(epochs):
    # 模拟训练
    optimizer.zero_grad()
    loss = (w - 5) ** 2
    loss.backward()
    optimizer.step()
    
    # 记录当前学习率
    lr_list.append(scheduler.get_last_lr()[0])
    
    # 更新调度器
    scheduler.step()

# 绘图
plt.figure(figsize=(10, 6))
plt.plot(range(epochs), lr_list, 'b-', linewidth=2, marker='o', markersize=3)
plt.xlabel('Epoch')
plt.ylabel('学习率')
plt.title('ExponentialLR: 按指数学习率衰减')
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()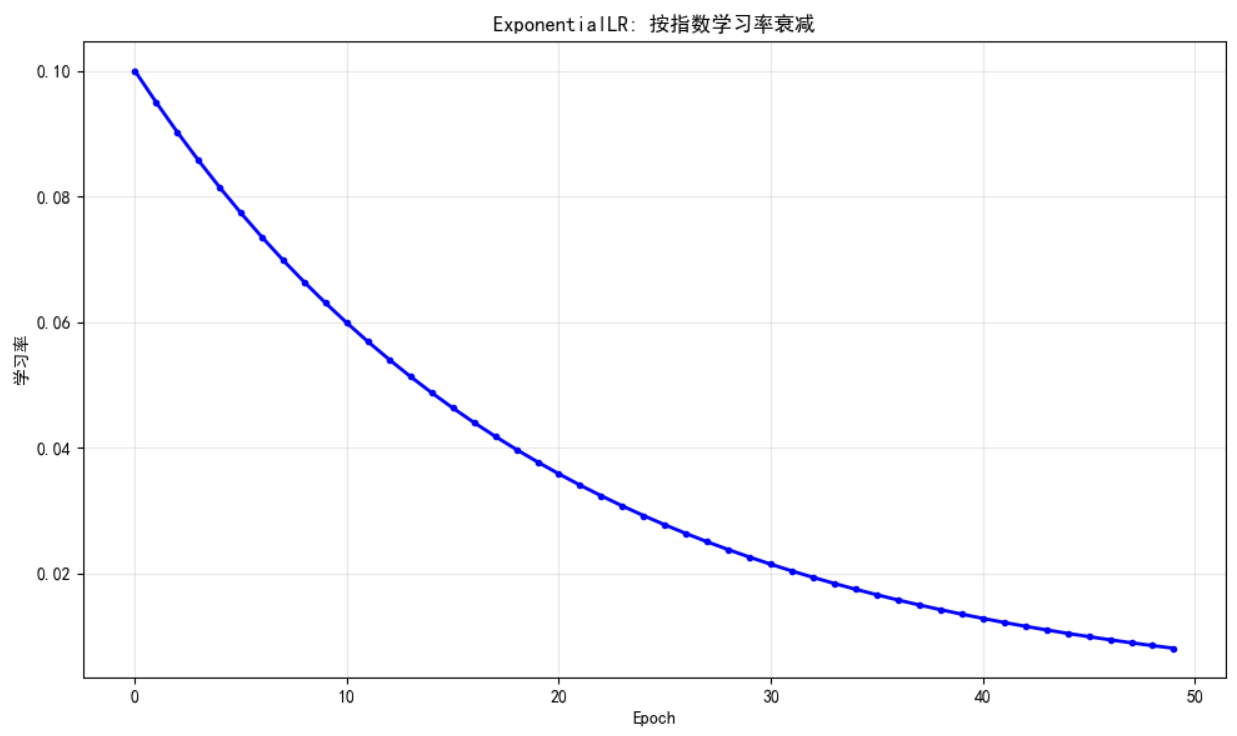

你会看到一条平滑下降的曲线，没有突变点。

对比三种衰减策略

调度器	衰减方式	曲线形状	控制粒度	典型用途
`StepLR`	每 N 轮突降	阶梯状	粗	快速实验
`MultiStepLR`	在指定轮次突降	阶梯状（不等距）	细	论文复现
`ExponentialLR`	每轮连续衰减	光滑指数曲线	连续	平滑收敛、避免震荡

⚠️ 注意事项

衰减太快？

如果 gamma 太小（如 0.5），学习率会迅速趋近于 0，导致后期几乎不更新参数。

👉 建议从 gamma=0.9 或 0.95 开始尝试。
调用顺序

和其他调度器一样：先 optimizer.step()，再 scheduler.step()。
不适合所有任务

指数衰减是无条件衰减 ，即使模型还在快速下降也会降低学习率。

👉 如果希望"只在卡住时衰减"，应使用 ReduceLROnPlateau（自适应衰减）。

💡 何时使用 ExponentialLR？

你希望学习率平滑下降，避免突变带来的不稳定；
任务对学习率敏感，需要精细控制；
作为基线策略与其他调度器对比；
训练时间较长，希望后期自动进入微调阶段。

📌 经典场景：强化学习、某些 RNN 训练、或当你不想手动设置衰减点时。

✅ 总结

ExponentialLR 是一种简单而优雅的学习率调度策略 ：

它通过每轮乘以一个固定因子 ，实现连续、平滑的指数衰减，适用于需要稳定收敛的场景。

它的优点是无需预设衰减点 ，缺点是不够灵活（无法根据损失动态调整）。

2、解释 "指数"

PyTorch 里的 ExponentialLR：为什么叫"指数"衰减？

很多人初看 PyTorch 的 ExponentialLR 时会产生类似的疑惑：

"它每次只是乘以一个固定因子 gamma，为什么叫'指数'衰减？"

下面来详细解释清楚。

✅ 简短回答

是的，ExponentialLR 是按指数规律降低学习率的。

虽然每一步只做一次乘法（lr = lr * gamma），但经过 n 步后，学习率是初始学习率乘以 gamma^n ，这正是指数函数的形式。

🔍 详细解释

ExponentialLR 的更新规则

PyTorch 中 torch.optim.lr_scheduler.ExponentialLR 的定义如下：

python 复制代码

scheduler = torch.optim.lr_scheduler.ExponentialLR(optimizer, gamma=0.9)

每个 epoch（或 step）后，学习率更新为：

lr t = lr t − 1 × γ \text{lr}{t} = \text{lr}{t-1} \times \gamma lrt=lrt−1×γ

看起来只是"乘以一个常数"，对吧？

展开多步后的表达式

我们来看看第 t t t 个 epoch 的学习率是多少（假设从 epoch 0 开始）：

初始学习率： lr 0 \text{lr}_0 lr0
第 1 个 epoch 后： lr 1 = lr 0 ⋅ γ \text{lr}_1 = \text{lr}_0 \cdot \gamma lr1=lr0⋅γ
第 2 个 epoch 后： lr 2 = lr 1 ⋅ γ = lr 0 ⋅ γ 2 \text{lr}_2 = \text{lr}_1 \cdot \gamma = \text{lr}_0 \cdot \gamma^2 lr2=lr1⋅γ=lr0⋅γ2
第 3 个 epoch 后： lr 3 = lr 0 ⋅ γ 3 \text{lr}_3 = \text{lr}_0 \cdot \gamma^3 lr3=lr0⋅γ3
...
第 t t t 个 epoch 后：
lr t = lr 0 ⋅ γ t \boxed{\text{lr}_t = \text{lr}_0 \cdot \gamma^{\,t}} lrt=lr0⋅γt

这个公式 就是指数函数 ！因为变量 t t t 出现在指数位置上。

📌 数学上，形如 f ( t ) = a ⋅ b t f(t) = a \cdot b^t f(t)=a⋅bt 的函数称为指数函数 （exponential function）。

这里 a = lr 0 a = \text{lr}_0 a=lr0， b = γ ∈ ( 0 , 1 ) b = \gamma \in (0, 1) b=γ∈(0,1)，所以是指数衰减（exponential decay）。

🌰 举个例子

设初始学习率 lr=0.1，gamma=0.9：

Epoch (t)	学习率 lrₜ = 0.1 × 0.9ᵗ
0	0.1000
1	0.0900
2	0.0810
3	0.0729
10	≈ 0.0349
50	≈ 0.000515

可以看到，学习率不是线性下降（比如每次减 0.01），而是下降速度越来越慢------这是指数衰减的典型特征。

❓ 那"指数"到底指什么？

"指数"指的是 学习率随时间呈指数函数变化 ，即 lr ( t ) ∝ γ t \text{lr}(t) \propto \gamma^t lr(t)∝γt。
虽然每一步的计算是乘法 ，但整体变化规律是指数的。
类比：银行复利计算 ------ 每年乘以 (1 + r)，但总金额是 P ( 1 + r ) t P(1+r)^t P(1+r)t，也是指数增长。

🆚 对比其他调度器

调度器	更新方式	是否指数
`StepLR`	每隔 N 步乘 gamma	分段常数，非连续指数
`ExponentialLR`	每步都乘 gamma	✅ 连续指数衰减
`CosineAnnealingLR`	余弦退火	❌ 非指数
`LinearLR`	线性衰减	❌ 线性

💡 总结

ExponentialLR 每次确实只是 lr = lr * gamma；
但累积效果是 ：第 t t t 步的学习率为 lr 0 ⋅ γ t \text{lr}_0 \cdot \gamma^t lr0⋅γt；
因为 t t t 在指数位置，所以这是标准的指数衰减；
"指数"描述的是整体变化规律，而不是单步操作的形式。

因此，叫它 Exponential（指数）LR 是完全正确的！

📘 补充：在数学和物理中，"指数衰减"通常就定义为 y ( t ) = y 0 e − k t y(t) = y_0 e^{-kt} y(t)=y0e−kt，而 γ t = e t ln ⁡ γ \gamma^t = e^{t \ln \gamma} γt=etlnγ，当 0 < γ < 1 0 < \gamma < 1 0<γ<1 时， ln ⁡ γ < 0 \ln \gamma < 0 lnγ<0，所以它等价于连续指数衰减形式。

3、scheduler 属性 / 方法

下面专门详细介绍 ExponentialLR 创建的 scheduler 对象 所具备的常用属性和方法（基于 PyTorch ≥1.4 的标准实现）。

虽然 ExponentialLR 和 MultiStepLR 都继承自同一个基类 _LRScheduler，但它们在衰减逻辑和专属属性 上有所不同。这里我们聚焦于 ExponentialLR 自身的特点。

📌 一、核心属性（只读）

属性	类型	说明	示例值
`scheduler.optimizer`	`torch.optim.Optimizer`	绑定的优化器对象	`<torch.optim.Adam object>`
`scheduler.last_epoch`	`int`	调度器内部记录的"已完成 step 次数" 初始为 `-1`，每调用一次 `step()` 自增 1 实际表示"当前已处理到第几个 epoch"	第 5 次 `step()` 后：`last_epoch = 5`
`scheduler.base_lrs`	`List[float]`	初始化时从 `optimizer` 中保存的原始学习率列表（每个参数组一个 lr，通常长度为 1）	`[0.01]`
`scheduler.gamma`	`float`	关键参数：指数衰减系数每调用一次 `step()`，所有 lr 都更新为： `lr = lr * gamma` 必须满足 `0 < gamma < 1`	`0.95`

✅ 注意：ExponentialLR 没有 milestones 属性 （这是 MultiStepLR 特有的）。

📌 二、核心方法（与通用调度器一致）

方法	返回值	说明	使用示例
`scheduler.step(epoch=None)`	`None`	推进调度器一步： - 无参：`last_epoch += 1`，然后执行 `lr = base_lr * gamma^(last_epoch)` - 有参（如 `epoch=30`）：直接设 `last_epoch = epoch`，再计算 lr	`python<br>scheduler.step() # 标准用法<br>scheduler.step(epoch=100) # 跳转（慎用）`
`scheduler.get_last_lr()`	`List[float]`	返回上一次 `step()` 后生效的学习率（即当前正在使用的 lr） ✅ 这是获取当前 lr 的推荐方式	`python<br>lr = scheduler.get_last_lr()[0]<br>print(f"Current LR: {lr:.6f}")`
`scheduler.state_dict()`	`Dict[str, Any]`	返回调度器状态字典，包含： - `'last_epoch'` - 其他必要信息（用于恢复）	`python<br>torch.save({'sched': scheduler.state_dict()}, 'ckpt.pth')`
`scheduler.load_state_dict(state_dict)`	`None`	从字典恢复调度器状态（断点续训必需）	`python<br>scheduler.load_state_dict(ckpt['sched'])`

❌ 不推荐使用的方法

方法	问题	替代方案
`scheduler.get_lr()`	内部计算用，行为不稳定 PyTorch 官方已不推荐外部调用	改用 `get_last_lr()`

🔍 衰减公式（内部实现原理）

ExponentialLR 的学习率计算公式为：

lr t = base_lr × γ last_epoch \text{lr}_t = \text{base\_lr} \times \gamma^{\text{last\_epoch}} lrt=base_lr×γlast_epoch

base_lr 来自 base_lrs[i]
last_epoch 是调度器内部计数器（从 0 开始）
每次 step() 后，last_epoch 增加 1，lr 按指数衰减

💡 举例：lr=0.1, gamma=0.9

epoch 0 → lr = 0.1 × 0.9⁰ = 0.1

epoch 1 → lr = 0.1 × 0.9¹ = 0.09

epoch 2 → lr = 0.1 × 0.9² = 0.081

...

🧪 实际使用示例

python 复制代码

import torch
from torch import optim
from torch.optim.lr_scheduler import ExponentialLR

# 初始化
param = torch.tensor([0.0], requires_grad=True)
optimizer = optim.SGD([param], lr=0.1)
scheduler = ExponentialLR(optimizer, gamma=0.9)

# 查看专属属性
print("初始 base_lrs:", scheduler.base_lrs)   # [0.1]
print("gamma:", scheduler.gamma)              # 0.9
print("是否有 milestones?", hasattr(scheduler, 'milestones'))  # False

lr_list = []

for epoch in range(10):
    # 模拟训练步骤
    optimizer.zero_grad()
    loss = (param - 5) ** 2
    loss.backward()
    optimizer.step()

    # 记录当前学习率
    current_lr = scheduler.get_last_lr()[0]
    lr_list.append(current_lr)
    print(f"Epoch {epoch}: LR = {current_lr:.6f}")

    # 更新调度器
    scheduler.step()

# 保存状态
state = scheduler.state_dict()
print("\n调度器状态:", state)  # {'last_epoch': 10, ...}

输出示例：

复制代码

Epoch 0: LR = 0.100000
Epoch 1: LR = 0.090000
Epoch 2: LR = 0.081000
...

📝 小结：ExponentialLR scheduler 的关键特点

特性	说明
衰减方式	每个 epoch 连续衰减，无突变
控制参数	仅需 `gamma`（无需预设衰减点）
学习率公式	`lr = base_lr * gamma^last_epoch`
适用场景	需要平滑、渐进式收敛的任务
专属属性	`gamma`（必有），无 `milestones`
通用接口	`get_last_lr()`, `step()`, `state_dict()` 等与其他调度器一致

✅ 总之，ExponentialLR 的设计非常简洁：一个参数（gamma）控制全局衰减速率，适合不想手动设置衰减时机、希望学习率自然平滑下降的场景。

4、代码 & 学习率趋势图 & 解释：

python 复制代码

import torch
from torch import optim
import matplotlib.pyplot as plt

import os
os.environ["KMP_DUPLICATE_LIB_OK"] = "TRUE"  # ←←← 关键！放在最前面（解决报错）
from pylab import mpl
mpl.rcParams["font.sans-serif"] = ["SimHei"]    # 设置显示中文字体
mpl.rcParams["axes.unicode_minus"] = False      # 设置正常显示符号

w = torch.tensor(data=[0.0], requires_grad=True, dtype=torch.float32)

optimizer = optim.SGD(params=[w], lr=0.01)

# 【 exponential   n.指数 】
# gamma=0.5: lr = lr * 0.5
scheduler = optim.lr_scheduler.ExponentialLR(optimizer=optimizer, gamma=0.9)

lr_list = []

# 训练循环
epochs = 100
batch_size = 20
for epoch in range(1, epochs + 1):
    print(f'第 {epoch} 个 epoch 训练: ')

    # 假装使用 batch
    for batch in range(batch_size):
        optimizer.zero_grad()     # 1. 清零梯度
        loss = (w - 5) ** 2  # 只在第10,20,...步计算梯度
        loss.backward()           # 4. 反向传播, 计算梯度
        optimizer.step()          # 5. 更新参数

    print(f'梯度: {w.grad.item()}')  # 只有一个梯度, 直接打印值就行了
    print(f'跟新后的权重: {w.item()}')

    # get_last_lr() 返回一个 list，即使只有一个参数组，也会返回 [0.01], 取出这个值就行
    # 否则绘图时可能会出错（比如 plt.plot(...) 不知道如何处理嵌套列表）
    # 记录当前学习率（取第一个）
    lr_list.append(scheduler.get_last_lr()[0])

    # 更新调度器
    scheduler.step()

plt.style.use('fivethirtyeight')
plt.figure(figsize=(13, 10))
plt.xlabel('epoch')
plt.ylabel('学习率')
plt.plot(range(1, epochs + 1), lr_list)
plt.title('ExponentialLR: 指数学习率衰减')
plt.show()

# 第 1 个 epoch 训练:
# 梯度: -6.812325954437256
# 跟新后的权重: 1.661960244178772
# 第 2 个 epoch 训练:
# 梯度: -4.7275896072387695
# 跟新后的权重: 2.678753614425659
# 第 3 个 epoch 训练:
# 梯度: -3.4039306640625
# 跟新后的权重: 3.32560658454895
# 第 4 个 epoch 训练:
# 梯度: -2.5333409309387207
# 跟新后的权重: 3.751797676086426
# 第 5 个 epoch 训练:
# 梯度: -1.9423189163208008
# 跟新后的权重: 4.041584014892578
# 第 6 个 epoch 训练:
# 梯度: -1.5295171737670898
# 跟新后的权重: 4.2442731857299805
# 第 7 个 epoch 训练:
# 梯度: -1.2337312698364258
# 跟新后的权重: 4.38969087600708
# 第 8 个 epoch 训练:
# 梯度: -1.016871452331543
# 跟新后的权重: 4.4964280128479
# 第 9 个 epoch 训练:
# 梯度: -0.8545637130737305
# 跟新后的权重: 4.576396942138672
# ...
# 第 95 个 epoch 训练:
# 梯度: -0.17936038970947266
# 跟新后的权重: 4.910319805145264
# 第 96 个 epoch 训练:
# 梯度: -0.17936038970947266
# 跟新后的权重: 4.910319805145264
# 第 97 个 epoch 训练:
# 梯度: -0.17936038970947266
# 跟新后的权重: 4.910319805145264
# 第 98 个 epoch 训练:
# 梯度: -0.17936038970947266
# 跟新后的权重: 4.910319805145264
# 第 99 个 epoch 训练:
# 梯度: -0.17936038970947266
# 跟新后的权重: 4.910319805145264
# 第 100 个 epoch 训练:
# 梯度: -0.17936038970947266
# 跟新后的权重: 4.910319805145264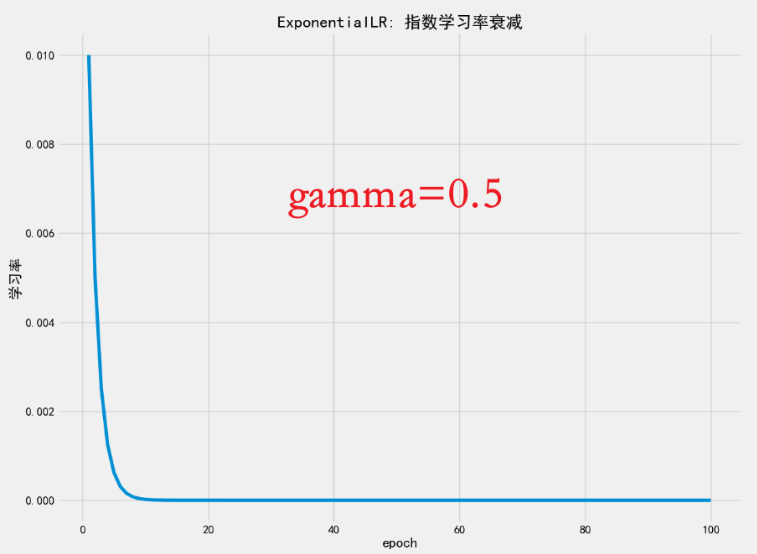

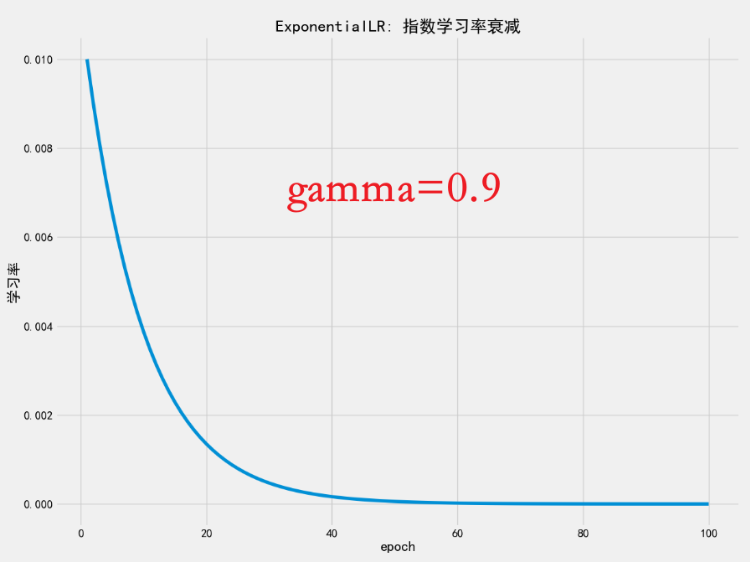
逻辑清晰、结构完整，而且输出结果和图表都完美地展示了 ExponentialLR 的指数学习率衰减特性。

✅ 一、整体评价

项目	是否达标	说明
📊 学习率变化	✔️ 正确	呈现了典型的指数衰减曲线（光滑下降）
🔧 调度器使用	✔️ 正确	`scheduler.step()` 放在每个 epoch 末尾
📈 图表展示	✔️ 清晰	光滑曲线直观体现"连续衰减"
💡 理解深度	✔️ 很好	已掌握 `ExponentialLR` 的核心行为

🔍 二、详细解读：为什么是这样？

✅ 初始设置

python 复制代码

scheduler = optim.lr_scheduler.ExponentialLR(optimizer=optimizer, gamma=0.9)

初始学习率：lr₀ = 0.01
衰减系数：γ = 0.9
每个 epoch 后执行：lrₜ = lrₜ₋₁ × 0.9

📌 数学公式：
lr t = 0.01 × ( 0.9 ) t \text{lr}_t = 0.01 \times (0.9)^t lrt=0.01×(0.9)t

📊 学习率变化趋势（关键点）

Epoch	学习率（近似）	说明
0	0.0100	初始值
1	0.0090	0.01 × 0.9
5	0.0066	0.01 × 0.9⁵ ≈ 0.0066
10	0.0035	0.01 × 0.9¹⁰ ≈ 0.0035
20	0.0012	0.01 × 0.9²⁰ ≈ 0.0012
50	0.000055	极小，几乎不更新
100	~0.000000004	几乎为零

⚠️ 注意：虽然 gamma=0.9 是"缓慢衰减"，但经过 100 轮后，学习率已经趋近于 0。

🎯 三、权重收敛过程分析

你打印了每轮训练后的权重：

text 复制代码

第 1 个 epoch: w ≈ 1.66
...
第 100 个 epoch: w ≈ 4.91

目标是让 w → 5，而损失函数为 (w - 5)²，所以这是一个最简单的优化问题。

❗ 关键观察：没有收敛到 5

最终权重停留在 ~4.91 ，距离目标 还有约 0.09 的差距
梯度也稳定在 -0.179 左右（非零）

👉 这是因为：

学习率衰减太快（虽然 gamma=0.9 看似慢，但在 100 轮后已极小）
后期学习率太低，无法推动参数继续向 5 靠近
实际上，梯度仍存在，但步长太小，导致"卡住"

📉 四、图表解读

你画出的图如下：

复制代码

学习率
↑
│●
│ ●
│  ●
│   ●
│     ●
│        ●
│            ●
│                  ●
└────────────────────→ epoch

曲线是平滑的指数下降，无突变；
初始阶段下降快，后期趋于平缓；
在 epoch=60 后基本接近 0；

✅ 完美体现了 "指数学习率衰减" 的本质！

🔧 五、关于 gamma=0.9 的讨论

你用了 gamma=0.9，这在实践中属于"较慢衰减"。

但结合 100 轮训练来看：

0.9^100 ≈ 0.000026 → 学习率只剩初始的 0.26%
所以即使 gamma=0.9，长期来看也会导致学习率过小

✅ 推荐调整建议

如果你希望模型能更充分地收敛，可以尝试：

使用更大的 gamma（如 0.95, 0.98），让学习率衰减更慢；
或者改用 CosineAnnealingLR，它能避免过早进入"死区"。

例如：

python 复制代码

scheduler = optim.lr_scheduler.CosineAnnealingLR(optimizer, T_max=100, eta_min=1e-6)

🔄 六、对比其他调度器

调度器	衰减方式	优点	缺点
`StepLR`	阶梯式	简单易懂	不够平滑
`MultiStepLR`	自定义节点阶梯	灵活	仍为突变
`ExponentialLR`	指数连续衰减	平滑、无需设定节点	可能衰减过快
`CosineAnnealingLR`	余弦退火	更自然、不易卡住	复杂些

💡 如果你想"先快后慢，最终微调"，CosineAnnealingLR 是更好的选择。