动态规划入门:从"傻傻递归"到"聪明求解"
你有没有遇到过这样的问题?
- 计算斐波那契数列时,数字稍微大一点程序就卡住了?
- 解决一个复杂问题时,发现很多子问题被重复计算了无数次?
- 想要找到最优解,但暴力搜索的时间又太长?
别担心,今天我要给你介绍一种强大的算法思想------动态规划,它能帮你优雅地解决这些问题!
什么是动态规划?
动态规划(Dynamic Programming,简称DP)听起来很高大上,但其实它的核心思想很简单:不要重复计算已经算过的东西。
想象一下,你在做数学题,遇到一道复杂的计算题。聪明的你会先把中间结果记在草稿纸上,下次用到时直接看结果,而不是重新算一遍。这就是动态规划的核心思想!
让我们从一个经典的例子开始:斐波那契数列。
问题描述:
斐波那契数列的定义很简单:
- F(0) = 0
- F(1) = 1
- F(n) = F(n-1) + F(n-2) (n ≥ 2)
方法1:朴素的递归(不推荐)
cpp
#include <iostream>
using namespace std;
int fib_recursive(int n) {
if (n <= 1) return n;
return fib_recursive(n-1) + fib_recursive(n-2);
}
int main() {
int n = 40;
cout << "计算F(" << n << ")..." << endl;
cout << "结果: " << fib_recursive(n) << endl;
return 0;
}问题:试试计算F(40),你会发现程序要跑很久。为什么?因为它像下图这样做了大量重复计算:
计算F(5):
F(5)
/ \
F(4) F(3)
/ \ / \
F(3) F(2) F(2) F(1)
/ \
F(2) F(1)
... 很多重复计算!方法2:动态规划解法
cpp
#include <iostream>
#include <vector>
using namespace std;
int fib_dp(int n) {
if (n <= 1) return n;
// 创建一个数组来保存计算结果
vector<int> dp(n + 1);
dp[0] = 0; // F(0)
dp[1] = 1; // F(1)
// 从小问题开始,逐步解决大问题
for (int i = 2; i <= n; i++) {
dp[i] = dp[i-1] + dp[i-2];
}
return dp[n];
}
int main() {
int n = 40;
cout << "计算F(" << n << ")..." << endl;
cout << "结果: " << fib_dp(n) << endl;
return 0;
}效果对比:
- 递归方法计算F(40):大约需要1秒以上
- 动态规划方法计算F(40):几乎瞬间完成
- 计算F(100)?递归方法可能永远算不完,动态规划方法还是瞬间完成!
问题描述
你正在爬楼梯,每次可以爬1阶或2阶。问爬到第n阶有多少种不同的方法?
示例
- n=1:1种方法(爬1阶)
- n=2:2种方法(1+1 或 2)
- n=3:3种方法(1+1+1, 1+2, 2+1)
动态规划解法
cpp
#include <iostream>
#include <vector>
using namespace std;
int climbStairs(int n) {
if (n <= 2) return n;
// 1. 定义状态:dp[i]表示爬到第i阶的方法数
vector<int> dp(n + 1);
// 2. 初始化
dp[0] = 1; // 不爬也是一种方法
dp[1] = 1; // 爬到第1阶:1种方法
dp[2] = 2; // 爬到第2阶:2种方法
// 3. 状态转移方程:dp[i] = dp[i-1] + dp[i-2]
// 4. 计算顺序:从3开始
for (int i = 3; i <= n; i++) {
dp[i] = dp[i-1] + dp[i-2];
}
// 5. 返回结果
return dp[n];
}
int main() {
for (int n = 1; n <= 10; n++) {
cout << "爬到第" << n << "阶有" << climbStairs(n) << "种方法" << endl;
}
return 0;
}理解为什么是dp[i] = dp[i-1] + dp[i-2]:
- 要爬到第i阶,最后一步可能是:
- 从第i-1阶爬1阶上来
- 从第i-2阶爬2阶上来
- 所以,爬到第i阶的方法数 = 爬到第i-1阶的方法数 + 爬到第i-2阶的方法数
动态规划的五个核心步骤
记住这五个步骤,其中一二是核心:
第一步:定义状态表示
一般会创建一个dp表用来记录状态,状态就是我们要记录的信息。比如在斐波那契问题中:
dp[i]表示第i个斐波那契数
第二步:找到状态转移方程
状态转移方程描述了状态之间的关系。比如:
dp[i] = dp[i-1] + dp[i-2]
第三步:初始化
给最基本的情况赋值。比如:
dp[0] = 0dp[1] = 1
第四步:确定计算顺序
从简单到复杂。比如:
- 从i=2开始,一直计算到n
第五步:返回结果
- 返回
dp[n]
空间优化技巧
很多时候,我们不需要保存所有的中间结果,可以使用滚动数组优化,即单独使用几个变量记录对应值,比如斐波那契数列:
优化前:O(n)空间
cpp
vector<int> dp(n + 1);
dp[0] = 0;
dp[1] = 1;
for (int i = 2; i <= n; i++) {
dp[i] = dp[i-1] + dp[i-2];
}优化后:O(1)空间
cpp
int fib(int n) {
if (n <= 1) return n;
int prev2 = 0; // 存储dp[i-2]
int prev1 = 1; // 存储dp[i-1]
int current; // 存储dp[i]
for (int i = 2; i <= n; i++) {
current = prev1 + prev2;
prev2 = prev1;
prev1 = current;
}
return current;
}经典例题
第 N 个泰波那契数

思路:
作为经典的动态规划的入门题型,题目已经给出 T n + 3 = T n + T n + 1 + T n + 2 Tn+3 = Tn + Tn+1 + Tn+2 Tn+3=Tn+Tn+1+Tn+2的条件,即从第四项开始,第四项的值为前三项的和,往后以此类推;
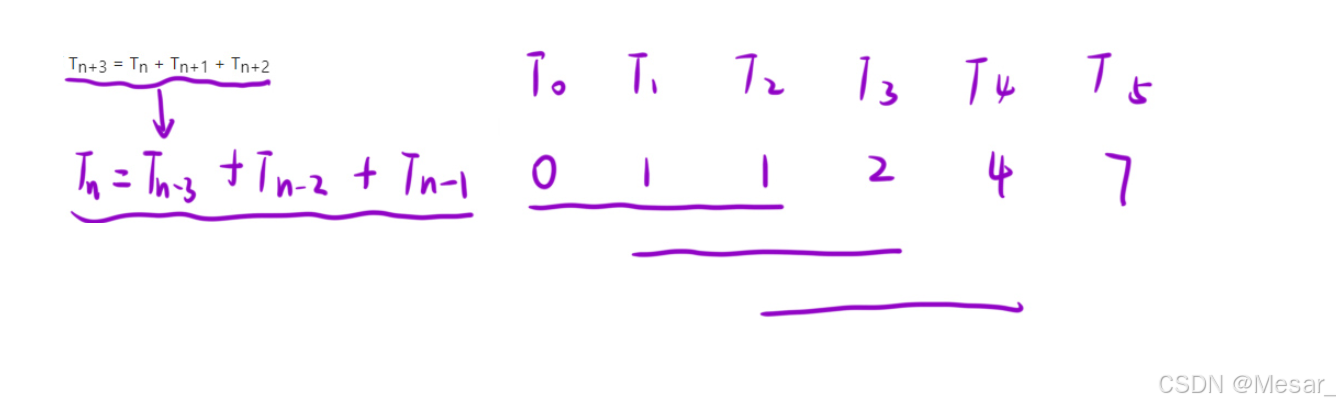
回忆动态规划的两个核心步骤:状态表示,状态转移方程;该题中的状态表示为:dp[i]表示第i个泰伯那契数的值;一般来说定义状态表示可以从经验与题目要求中获取,如第i个位置的值,且该题已经将第二步的状态转移方程都给出来了,所以大胆定义状态表示。

代码实现
cpp
class Solution
{
public:
int tribonacci(int n)
{
//1状态表示
//2状态转移方程
//3初始化(边界处理)
//4填表顺序
//5返回值
if(n==0)return n;
if(n==1||n==2)return 1;
vector<int> dp(n+1);//建dp表从第0个开始算
dp[0]=0,dp[1]=1,dp[2]=1;//初始化
for(int i=3;i<=n;i++)
{
dp[i]=dp[i-1]+dp[i-2]+dp[i-3];//根据状态方程填表
}
return dp[n];
}
};题目:三步问题

思路:根据题意,按每次可爬123阶楼梯推演得出下图,发现以第三阶为例:从第二阶爬一阶到第三阶这个过程需要先知道有多少种上第二阶的方法;且从第四阶开始,其总数为前面三阶楼梯的总和
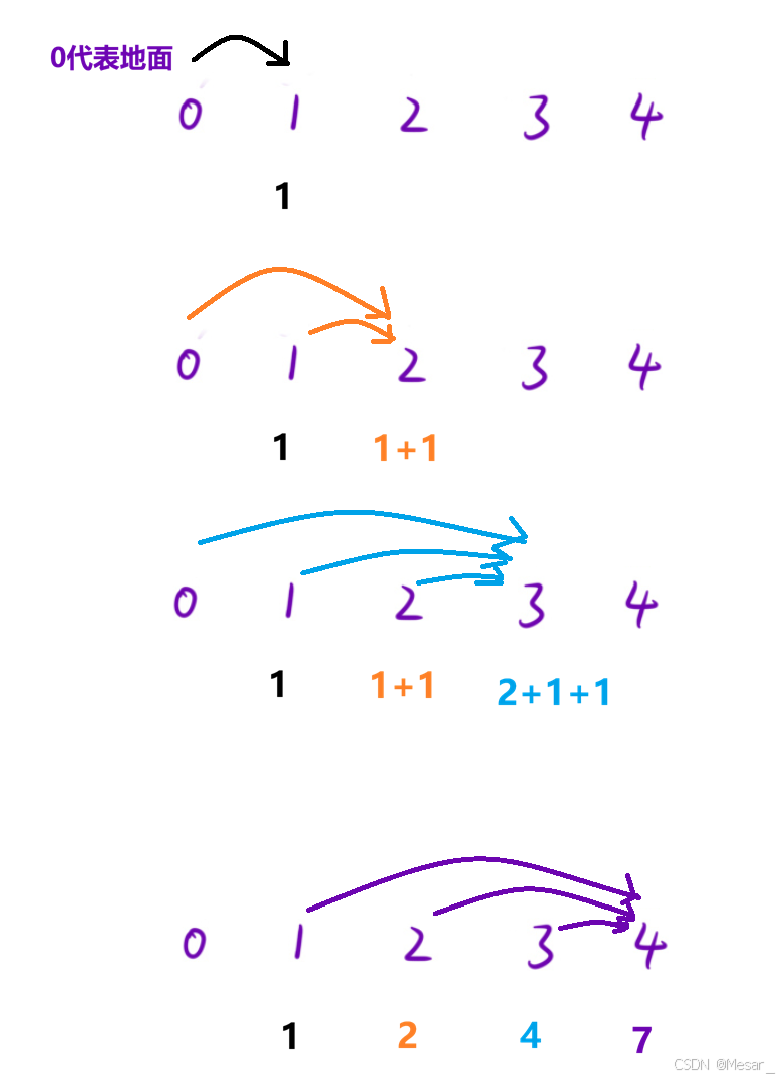
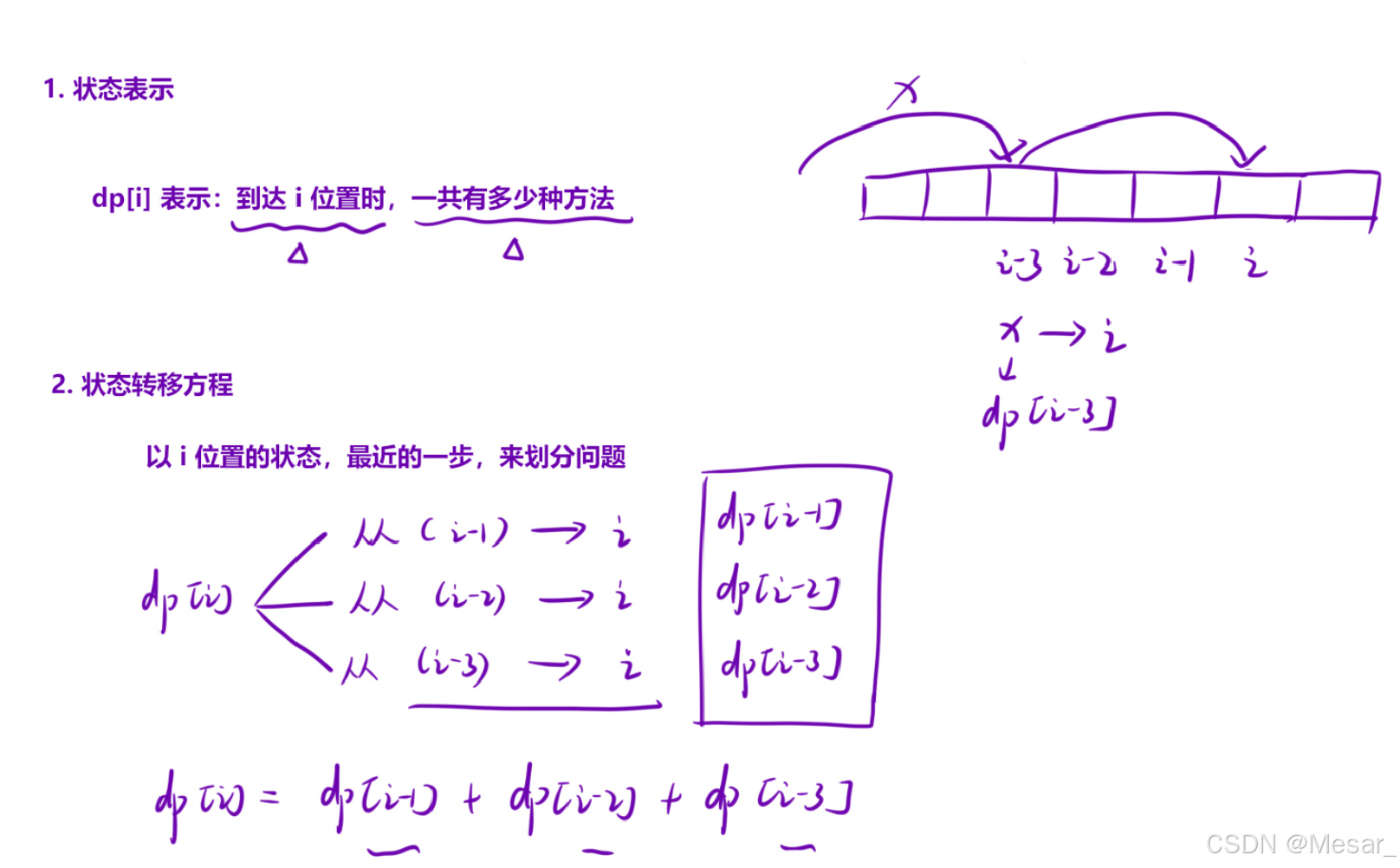
根据题目要求:求上到第n阶有多少种方式,所以可得出状态表示;又根据上图的推演得出状态转移方程,具体如下图:
代码实现:
cpp
class Solution
{
const int MOD=1000000007;
public:
int waysToStep(int n)
{
//前一阶梯
//1状态表示
//2状态转移方程
//3初始化
//4填充顺序
//5返回值
if(n==1)return n;
if(n==2)return n;
vector<int> dp(n+1);
dp[1]=1,dp[2]=2,dp[3]=4;//画图
for(int i=4;i<=n;++i)
dp[i]=((dp[i-1]+dp[i-2])%MOD+dp[i-3])%MOD;//防止溢出
return dp[n];
}
};题目:使用最小花费爬楼梯

爬楼梯示意,注意数组表示的都是阶梯,最后一个位置不是楼顶。
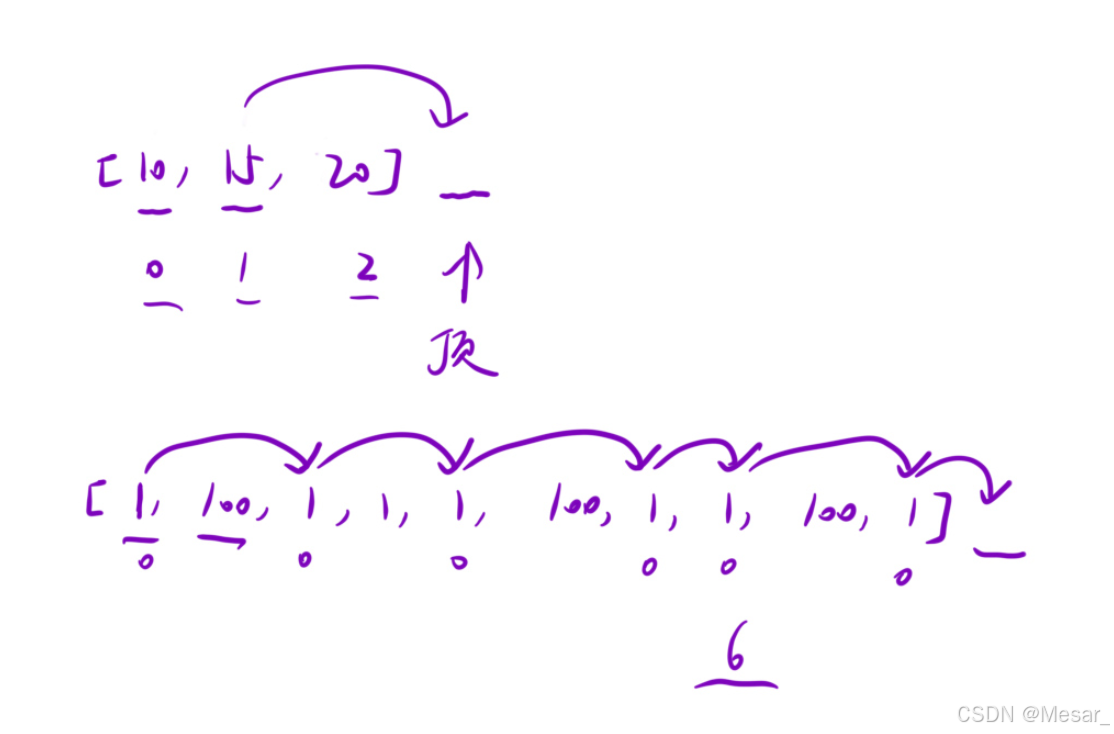
求状态表示和状态方程:
求到楼顶的最小花费,也就是以楼顶位置为结尾;所以dp[i]表示到达i位置时的最小花费;由于一次可以爬一阶或者两阶,所以到达i位置时的dp[i],必须先知道前两阶dp[i-1]和dp[i-2]的的花费,再选取较小值,状态转移方程由此得出
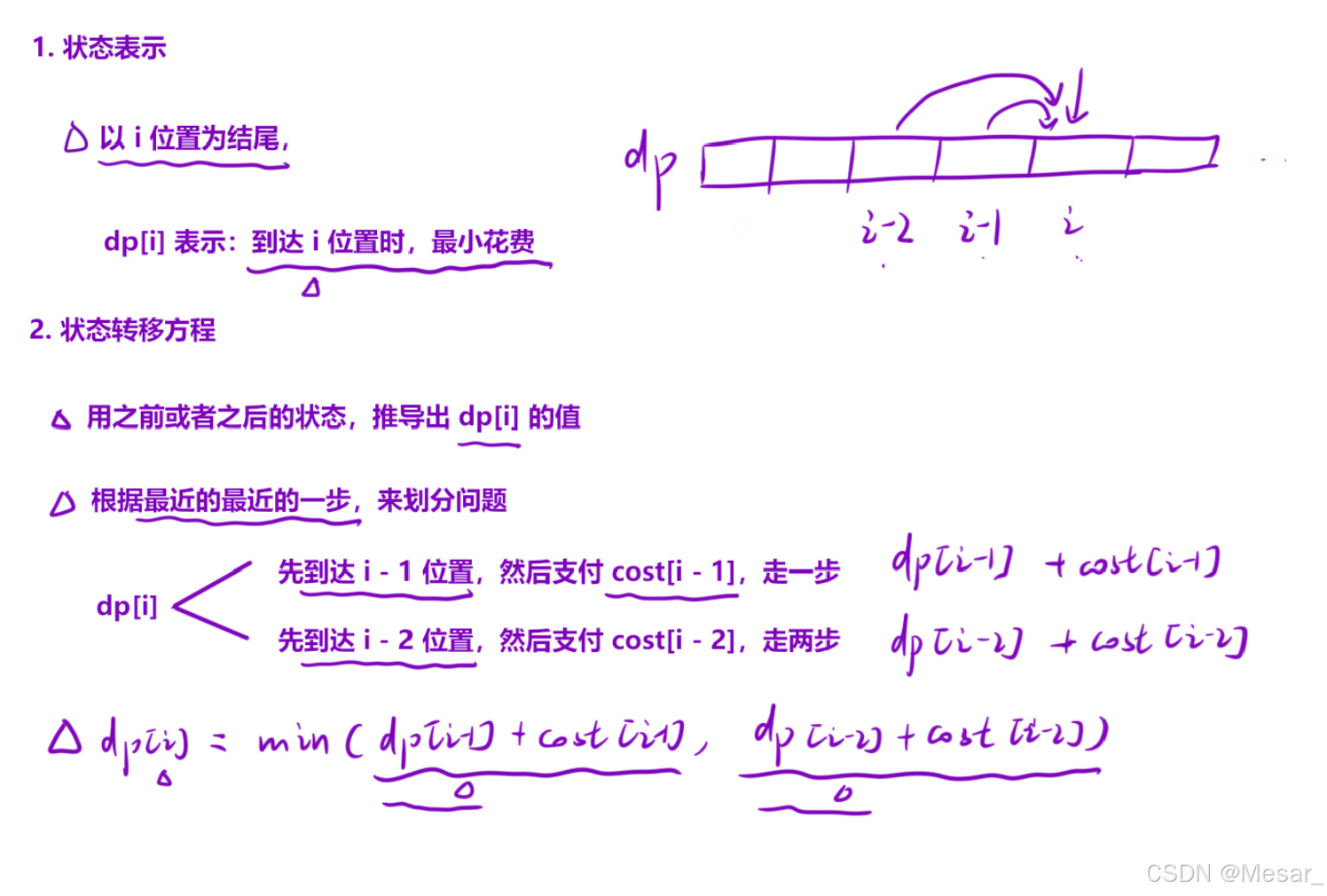
代码实现:
cpp
class Solution
{
public:
int minCostClimbingStairs(vector<int>& cost)
{
//cost中代表的都是楼梯,楼顶==cost.size
vector<int> dp(cost.size()+1);
dp[0]=dp[1]=0;
for(int i=2;i<=cost.size();++i)
dp[i]=min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);
return dp[cost.size()];//楼顶位置
}
};- 注意初始化: 可以从第一或者第二阶梯开始爬,即代表
dp[0]=dp[1]=0
题目:解码方法

解码示例:"12"可解码为AB,或者L一共两种方式;"226"可解码为BBF,VF,BZ三种解码方式;

返回一个数字字符串的解码方式,需要完全解码所有数字字符才能得知全部解码方式,所以状态方程可以表示为dp[i]以i位置为结尾的解码方式总数,与上题类似;因为可以有单个字符解码和两个字符共同解码两种方式,所以dp[i]需要先得出dp[i-1]以及dp[i-2];由此可得出状态转移方程;由于有06不等同于6,所以在初始化dp[0],dp[1]时需要判断处理

代码实现:
cpp
class Solution
{
public:
int numDecodings(string s)
{
vector<int> dp(s.size());
//初始化(单独解码)
dp[0]=s[0]!='0';//true->1
if(s.size()==1)return dp[0];
if(s[0]!='0'&&s[1]!='0')dp[1]=1;
//双字符解码
int t=10*(s[0]-'0')+s[1]-'0';
if(t>=10&&t<=26)dp[1]+=1;//字母范围在1-26;双字符需要从10-26(0*10不合要求)
for(int i=2;i<s.size();++i)
{
//单独解码
if(s[i]!='0')dp[i]+=dp[i-1];
//双字符
int t=10*(s[i-1]-'0')+s[i]-'0';
if(t>=10&&t<=26)dp[i]+=dp[i-2];
}
//for(auto e:dp)cout<<e;
return dp[s.size()-1];
}
};归纳
本篇只介绍了最入门的动态规划,以下内容看不懂也正常
如何识别动态规划问题?
当你遇到以下特征时,可以考虑使用动态规划:
- 求最优解:比如最少硬币、最大利润、最短路径
- 问题可以分解:大问题可以分解为小问题
- 有重叠子问题:同样的子问题被重复计算多次
- 有最优子结构:大问题的最优解可以由小问题的最优解得到
常见动态规划问题分类
| 问题类型 | 经典例题 | 状态定义技巧 |
|---|---|---|
| 一维DP | 爬楼梯、斐波那契 | dp[i]表示前i个元素的结果 |
| 二维DP | 最小路径和、最长公共子序列 | dp[i][j]表示到(i,j)位置的结果 |
| 背包问题 | 0-1背包、完全背包 | dp[i][w]表示前i个物品容量为w时的最优解 |
| 字符串DP | 编辑距离、最长回文子串 | dp[i][j]表示子串i到j的结果 |
常见错误
- 忘记初始化:dp[0]和dp[1]经常需要特殊处理
- 数组越界:访问dp[i-1]时要确保i≥1
- 错误的状态转移:仔细分析状态之间的关系
总结
动态规划就像搭积木:
- 找到最小的积木(基础情况)
- 知道怎么用小块积木搭大块(状态转移)
- 一块一块往上搭(从小问题到大问题)
记住关键点:
- 从暴力递归开始思考
- 找出重复计算的部分
- 用数组记录已计算的结果
- 找出状态转移方程
- 从简单到复杂逐步计算
其中最核心的的就是找到状态表示和状态转移方程,这是动态规划的核心,这个只能靠所谓的经验以及题目要求得出,如以i位置为结尾的什么什么定义出状态返程,再从最近的一步来划分问题,进而得出状态转移方程。