[模式识别-从入门到入土] 无监督学习

知乎：https://www.zhihu.com/people/byzh_rc

CSDN：https://blog.csdn.net/qq_54636039

注：本文仅对所述内容做了框架性引导，具体细节可查询其余相关资料or源码

参考文章：各方资料

文章目录

$模式识别-从入门到入土\] 无监督学习$
动态聚类模型
k-means <- 动态聚类模型
模拟C均值聚类FCM <- 动态聚类模型
层次聚类算法

无监督学习的分类

按建模方式分类:

基于样本概率分布模型 的聚类方法
e.g.高斯混合模型, 隐马尔科夫模型
基于样本间相似性度量 的聚类方法
e.g.动态聚类(k-means, FCM), 层次聚类

按模型类型分类:

概率模型：P(X∣Z)P(X|Z)P(X∣Z)（Z 为簇的隐变量）→ 软聚类
非概率模型：Y=f(X)Y=f(X)Y=f(X)（Y 为簇的硬划分）→ 硬聚类

动态聚类模型

目标: 簇内样本相似性高，簇间样本相似性低

	Fisher	动态聚类模型
核心关注	类内相似性 & 类间分离性	簇内相似性 & 簇间分离性
方法性质	监督学习（有类别标签）	无监督学习（无类别标签）

相似性度量 :

特征空间的距离度量(常用欧氏距离)
δ(xi,xj)=(xi−xj)T(xi−xj) \delta\left(x_{i},x_{j}\right)=\left(x_{i}-x_{j}\right)^T\left(x_{i}-x_{j}\right) δ(xi,xj)=(xi−xj)T(xi−xj)
准则函数 :

动态聚类的核心准则是簇内误差平方和最小化
J=∑i=1k∑x∈Ciδ(x,mi) J=\sum_{i=1}^{k}\sum_{x\in C_{i}}\delta\left(x, m_{i}\right) J=i=1∑kx∈Ci∑δ(x,mi)

准则函数只直接优化簇内紧凑性，但簇间分离性是被间接保证的

动态聚类-分类:

硬聚类: k-means
-> 簇内误差平方和最小化
软聚类: 模糊C均值聚类(FCM)
-> 簇内加权误差平方和最小化

k-means <- 动态聚类模型

第i个簇的中心/均值向量:mi=1Ni∑x∈Cix准则函数(簇内误差平方和):J=∑i=1kJi=∑i=1k∑x∈Ci∥x−mi∥2 \text{第 $i$ 个簇的中心/均值向量:}\quad m_i=\frac{1}{N_i}\sum_{x \in C_i}x \\ \text{准则函数(簇内误差平方和):}\quad J=\sum_{i=1}^{k} J_{i}=\sum_{i=1}^{k} \sum_{x \in C_{i}}\left\|x-m_{i}\right\|^{2} 第i个簇的中心/均值向量:mi=Ni1x∈Ci∑x准则函数(簇内误差平方和):J=i=1∑kJi=i=1∑kx∈Ci∑∥x−mi∥2

算法流程:

随机选k个样本作为初始各簇的中心m1,...,mkm_1,...,m_km1,...,mk
最小距离法则->将各个样本划分到k个类C1,...,CkC_1,...,C_kC1,...,Ck中
计算准则函数JJJ, 重新计算k个簇的中心m1,...,mkm_1,...,m_km1,...,mk
重复2和3, 直到m1,...,mkm_1,...,m_km1,...,mk不变 or 准则函数JJJ不减小

符号	含义说明
kkk	簇的数量
mim_imi	第iii个簇的中心（均值向量），i∈{1,2,...,k}i \in \{1,2,...,k\}i∈{1,2,...,k}
CiC_iCi	第iii个簇的样本集合，i∈{1,2,...,k}i \in \{1,2,...,k\}i∈{1,2,...,k}
xxx	单个样本
JJJ	准则函数(簇内误差平方和)
JiJ_iJi	第iii个簇的簇内误差平方和
NiN_iNi	第iii个簇中包含的样本数量

模拟C均值聚类FCM <- 动态聚类模型

当特征与分类结果呈复杂非线性 关系时，可借助先验知识提取模糊特征

虽会增加特征数量，但能将特征与分类的关系转化为线性

根据气温这个特征，对 "是否适合户外跑步" 进行分类

气温和 "适合跑步" 的关系是非线性的：

低于 5∘C5^\circ\text{C}5∘C → 不适合

5∘C∼25∘C5^\circ\text{C} \sim 25^\circ\text{C}5∘C∼25∘C → 适合

高于 25∘C25^\circ\text{C}25∘C → 不适合

结合先验知识，把 "气温" 这个原始特征拆分成 3 个模糊特征：

模糊特征 1：气温属于 "低温" 的隶属度（如 5∘C5^\circ\text{C}5∘C 时隶属度为 1，15∘C15^\circ\text{C}15∘C 时隶属度为 0）

模糊特征 2：气温属于 "适宜温度" 的隶属度（如 15∘C15^\circ\text{C}15∘C 时隶属度为 1，30∘C30^\circ\text{C}30∘C 时隶属度为 0）

模糊特征 3：气温属于 "高温" 的隶属度（如 30∘C30^\circ\text{C}30∘C 时隶属度为 1，15∘C15^\circ\text{C}15∘C 时隶属度为 0）

线性化关系 此时可以构建一个线性分类模型 ：
y=w1f1+w2f2+w3f3+by = w_1f_1 + w_2f_2 + w_3f_3 + by=w1f1+w2f2+w3f3+b

其中 f1,f2,f3f_1,f_2,f_3f1,f2,f3 是 3 个模糊特征的取值，w1,w2,w3w_1,w_2,w_3w1,w2,w3 是权重

-> 通过给 w2w_2w2 赋正值、w1,w3w_1,w_3w1,w3 赋负值，就能线性地判断：当 y>0y>0y>0 时适合跑步，否则不适合

准则函数:
Jf=∑j=1C∑i=1N[μj(xi)]b∥xi−mj∥2 J_f=\sum_{j=1}^{C} \sum_{i=1}^N [\mu_j(x_i)]^b\left\|x_i-m_{j}\right\|^{2} Jf=j=1∑Ci=1∑N[μj(xi)]b∥xi−mj∥2

算法流程:

参数初始化 ：设定聚类数目 C、模糊系数 b、收敛阈值 ε\varepsilonε
聚类中心初始化 ：随机生成 C 个聚类中心的初始值 mj(0)m_j^{(0)}mj(0)
更新隶属度 ：根据当前聚类中心，用隶属度公式计算所有样本的隶属度 μij(s)\mu_{ij}^{(s)}μij(s)
μij(s)=(1/∥xi−mj(s)∥2)1/(b−1)∑l=1C(1/∥xi−ml(s)∥2)1/(b−1) \mu_{ij}^{(s)} = \frac{\left(1 / \|\mathbf{x}_i - \mathbf{m}j^{(s)}\|^2\right)^{1/(b-1)}}{\sum{l=1}^{C} \left(1 / \|\mathbf{x}_i - \mathbf{m}_l^{(s)}\|^2\right)^{1/(b-1)}} μij(s)=∑l=1C(1/∥xi−ml(s)∥2)1/(b−1)(1/∥xi−mj(s)∥2)1/(b−1)
更新聚类中心 ：根据当前隶属度，用聚类中心公式计算新的聚类中心 mj(s+1)m_j^{(s+1)}mj(s+1)
mj(s+1)=∑i=1N[μij(s)]bxi∑i=1N[μij(s)]b \mathbf{m}j^{(s+1)} = \frac{\sum{i=1}^{N} [\mu_{ij}^{(s)}]^b \mathbf{x}i}{\sum{i=1}^{N} [\mu_{ij}^{(s)}]^b} mj(s+1)=∑i=1N[μij(s)]b∑i=1N[μij(s)]bxi
收敛判断 ：若 ∥m(s+1)−m(s)∥<ε\left\|m^{(s+1)}-m^{(s)}\right\|<\varepsilon m(s+1)−m(s) <ε，则停止迭代；否则令 s=s+1s=s+1s=s+1，返回步骤 3
样本分类 ：将每个样本划分到隶属度最大的类别中

算法输出:

C 个聚类的中心矢量 {m1,m2,⋯ ,mC}\{m_1,m_2,\cdots,m_C\}{m1,m2,⋯,mC}
模糊隶属度矩阵 μN×C\mu_{N\times C}μN×C（每行对应一个样本，每列对应一个类别）

优点：对满足正态分布 的数据聚类效果良好

缺点：对孤立点 / 异常值敏感（异常值会显著影响聚类中心的位置）

最优解推导: 拉格朗日乘数法

构造拉格朗日函数:
L=∑j=1C∑i=1N[μj(xi)]b∥xi−mj∥2+∑i=1Nλi[∑j=1Cμj(xi)−1] L=\sum_{j=1}^{C} \sum_{i=1}^N [\mu_j(x_i)]^b\left\|x_i-m_{j}\right\|^{2}+\sum_{i=1}^N \lambda_i \left[ \sum_{j=1}^C \mu_j(x_i)-1 \right] L=j=1∑Ci=1∑N[μj(xi)]b∥xi−mj∥2+i=1∑Nλi[j=1∑Cμj(xi)−1]

对 mjm_jmj 和 μj(xi)\mu_j(x_i)μj(xi) 分别求偏导并令其为 0，得到最优解的必要条件：

聚类中心更新公式
mj=∑i=1N[μj(xi)]bxi∑i=1N[μj(xi)]b(j=1,2,⋯ ,C) \mathbf{m}j = \frac{\sum{i=1}^{N} [\mu_j(\mathbf{x}_i)]^b \mathbf{x}i}{\sum{i=1}^{N} [\mu_j(\mathbf{x}_i)]^b} \quad (j = 1,2,\cdots,C) mj=∑i=1N[μj(xi)]b∑i=1N[μj(xi)]bxi(j=1,2,⋯,C)

含义：聚类中心是样本的加权平均，权重为隶属度的 b 次方

隶属度更新公式
μj(xi)=(1/∥xi−mj∥2)1/(b−1)∑l=1C(1/∥xi−ml∥2)1/(b−1)(i=1,2,⋯ ,N; j=1,2,⋯ ,C) \mu_j(\mathbf{x}_i) = \frac{\left(1 / \|\mathbf{x}_i - \mathbf{m}j\|^2\right)^{1/(b-1)}}{\sum{l=1}^{C} \left(1 / \|\mathbf{x}_i - \mathbf{m}_l\|^2\right)^{1/(b-1)}} \quad (i = 1,2,\cdots,N;\ j = 1,2,\cdots,C) μj(xi)=∑l=1C(1/∥xi−ml∥2)1/(b−1)(1/∥xi−mj∥2)1/(b−1)(i=1,2,⋯,N; j=1,2,⋯,C)

含义：样本到聚类中心的距离越近，隶属度越大；距离越远，隶属度越小

符号	含义
JfJ_fJf	FCM的准则函数
CCC	聚类数目
NNN	样本总数
μj(xi)\mu_j(x_i)μj(xi)	样本 xix_ixi 隶属于第 jjj 类的隶属度（0≤μj(xi)≤10 \leq \mu_j(x_i) \leq 10≤μj(xi)≤1）
bbb	模糊系数（b>1b>1b>1） -> 控制聚类模糊程度
mjm_jmj	第 jjj 类的聚类中心（矢量）
λi\lambda_iλi	拉格朗日乘数（第 iii 个样本的约束系数）
ε\varepsilonε	收敛阈值（预设参数，判断迭代是否停止）
μij(s)\mu_{ij}^{(s)}μij(s)	第 sss 次迭代中，样本 iii 隶属于第 jjj 类的隶属度
mj(s)m_j^{(s)}mj(s)	第 sss 次迭代的第 jjj 类聚类中心

层次聚类算法

动态聚类-分类:

分裂的(自上而下) -> 层次k-均值算法
凝聚的(自下而上) -> 凝聚聚类算法

层次k-均值算法:

一旦两个样本在开始时被分成不同的簇，即使两点间距非常接近，它们以后也不会聚在一起

把所有样本数据归到一个簇中
用k-means分成k个子簇
重复第2步, 直到满足终止条件

凝聚聚类算法:

确保距离的近的样本可以被分到相同的簇

把每个样本单独看成一个簇
找到两个距离最近的簇minD(ci,cj)minD(c_i,c_j)minD(ci,cj), 合并簇cic_ici和簇cjc_jcj
重复第2步, 直到满足终止条件

两个簇之间的距离/簇间的相似性/簇间连接:

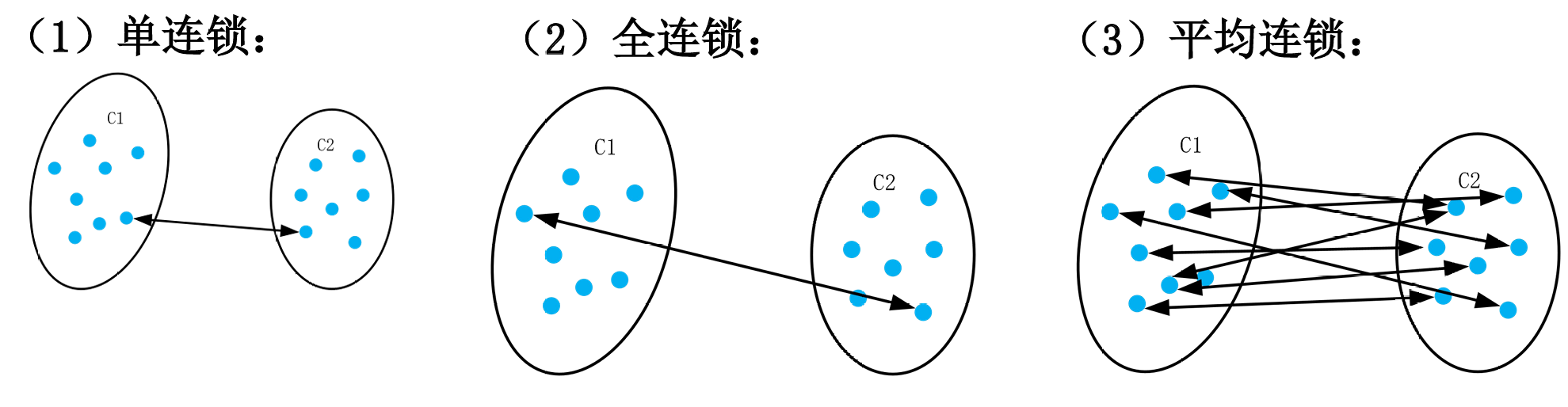
单连锁: 簇间距离为相距最近的两个点的距离
D(c1,c2)=min⁡x1∈c1, x2∈c2D(x1,x2) D(c_1, c_2) = \min_{x_1 \in c_1, \, x_2 \in c_2} D(x_1, x_2) D(c1,c2)=x1∈c1,x2∈c2minD(x1,x2)
全连锁: 簇间距离为相距最远的两个点的距离
D(c1,c2)=max⁡x1∈c1, x2∈c2D(x1,x2) D(c_1, c_2) = \max_{x_1 \in c_1, \, x_2 \in c_2} D(x_1, x_2) D(c1,c2)=x1∈c1,x2∈c2maxD(x1,x2)
平均连锁: 簇间距离为各点之间的距离的平均
D(c1,c2)=1∣c1∣1∣c2∣∑x1∈c1∑x2∈c2D(x1,x2) D(c_1, c_2) = \frac{1}{|c_1|} \frac{1}{|c_2|} \sum_{x_1 \in c_1} \sum_{x_2 \in c_2} D(x_1, x_2) D(c1,c2)=∣c1∣1∣c2∣1x1∈c1∑x2∈c2∑D(x1,x2)