算法基础-单源最短路

单源最短路

在图 G 中，假设vi 和 vj为图中的两个顶点，那么vi 到 vj路径上所经过边的权值之和就称为带权
路径⻓度。
由于 v i 到 v j 的路径可能有多条，将带权路径⻓度最短的那条路径称为最短路径。

最短路⼀般分为两类：
• 单源最短路，即图中⼀个顶点到其它各顶点的最短路径。
• 多源最短路，即图中每对顶点间的最短路径。

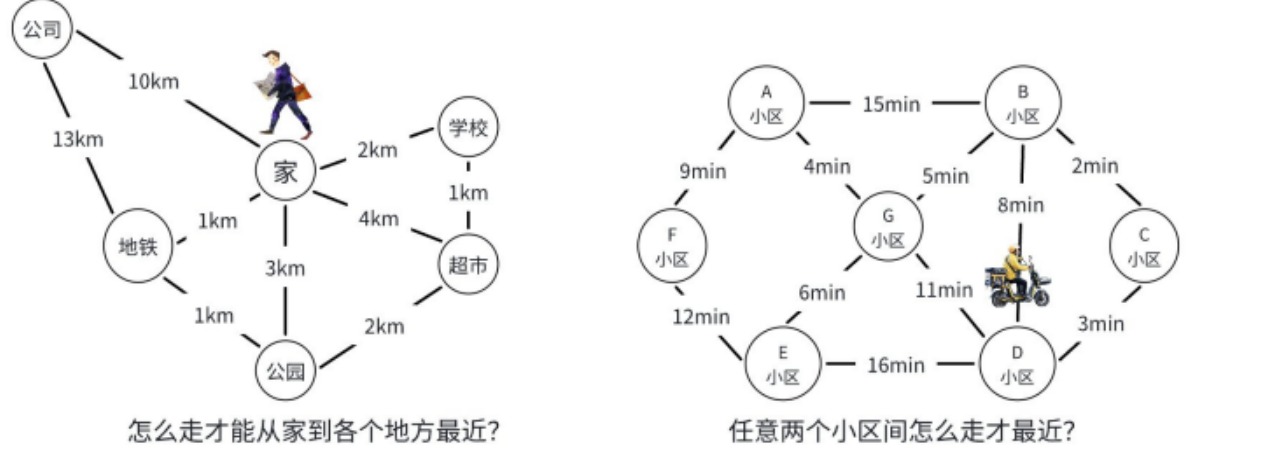
1 常规版 dijkstra 算法

Dijkstra 算法是 基于贪⼼思想的 单源最短路算法，求解的是" ⾮负权图 "上单源最短路径。

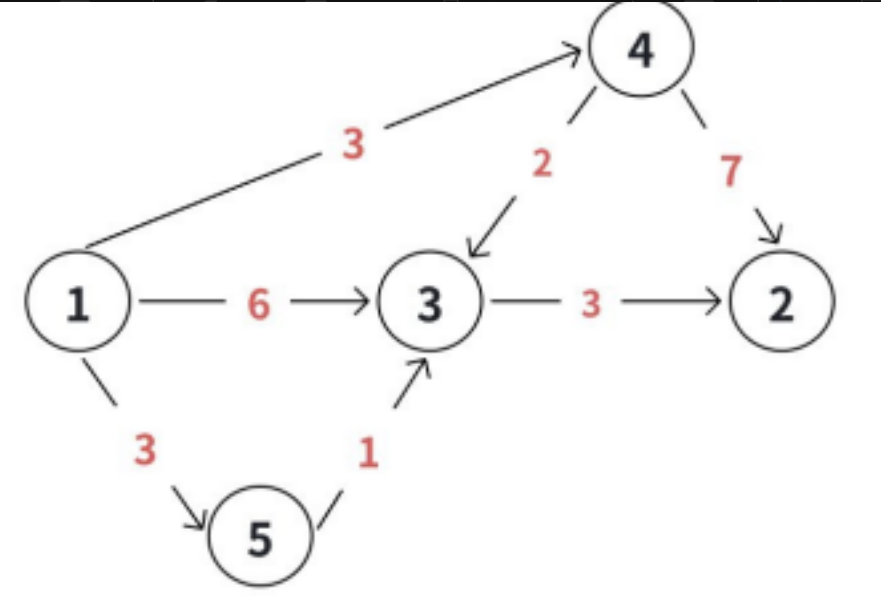
常规版 dijkstra 算法流程：
• 准备⼯作：
◦ 创建⼀个⻓度为 n 的 dist 数组，其中 dist[i] 表⽰从起点到 i 结点的最短路；
◦ 创建⼀个⻓度为 n 的 bool 数组 st ，其中 st[i] 表⽰ i 点是否已经确定了最短路。
• 初始化： dist[1] = 0 ，其余结点的 dist 值为⽆穷⼤，表⽰还没有找到最短路。
• 重复：在所有没有确定最短路的点中，找出最短路⻓度最⼩的点 u 。打上确定最短路的标记，然
后对 u 的出边进⾏松弛操作；
• 重复上述操作，直到所有点的最短路都确定。

代码实现：（⼤家会发现，这个代码⾮常像 prim 算法）

cpp 复制代码

void dijkstra()
{
    // 第一步：初始化dist数组（一开始都设为无穷大，除了起点）
    for(int i = 0; i <= n; i++) dist[i] = INF;
    dist[s] = 0;  // 起点到自己的距离是0（自己到自己不用走）
    
    // 第二步：外层循环（循环n-1次，后面解释为啥）
    for(int i = 1; i < n; i++)
    {
        // 子步骤1：找"没确定最短路"里，dist最小的点u
        int u = 0;  // 先把u初始化成0（0号点没用，只是临时值）
        for(int j = 1; j <= n; j++)  // 遍历所有点（1到n）
        {
            // 如果j点没确定最短路，且j点的dist比u点小，就把u换成j
            if(!st[j] && dist[j] < dist[u]) u = j;
        }
        
        // 子步骤2：给u打标记------u的最短路已经确定了，不用再改了
        st[u] = true;
        
        // 子步骤3：松弛操作（核心！逐行讲）
        for(auto& t : edges[u])  // 遍历u点能到的所有点（t是{v,w}，v=终点，w=路长）
        {
            int v = t.first, w = t.second;  // 把t拆开：v是u能到的点，w是这条路的长度
            // 如果"从起点到u的距离 + u到v的路长" 比 "原来记录的起点到v的距离" 更小，就更新
            if(dist[u] + w < dist[v])
            {
                dist[v] = dist[u] + w;  // 更新dist[v]为更小的距离
            }
        }
    }
    
    // 第三步：输出从起点到每个点的最短距离
    for(int i = 1; i <= n; i++)
    {
        cout << dist[i] << " ";
    }
}

2 堆优化版 dijkstra 算法

在常规版的基础上，⽤优先级队列去维护待确定最短路的结点。
堆优化版的 dijkstra 算法流程：
• 准备⼯作：
◦ 创建⼀个⻓度为 n 的 dist 数组，其中 dist[i] 表⽰从起点到 i 结点的最短路；
◦ 创建⼀个⻓度为 n 的 bool 数组 st ，其中 st[i] 表⽰ i 点是否已经确定了最短路；
◦ 创建⼀个⼩根堆，维护更新后的结点。（也就是需要确定最短路的结点）
• 初始化： dist[1] = 0 ，然后将 {0, s} 加到堆⾥；其余结点的 dist 值为⽆穷⼤，表⽰还没有找到最短路。
• 重复：弹出堆顶元素，如果该元素已经标记过，就跳过；如果没有标记过，打上标记，进⾏松弛操作。
• 重复上述操作，直到堆⾥⾯没有元素为⽌。
代码实现：（其实 prim 算法也有⼀个堆优化的版本，但是时间复杂度和 kk 算法相差⽆⼏，因此没有讲解）

cpp 复制代码

void dijkstra()
{
    // 步骤1：初始化dist数组为"无穷大"（比常规版的for循环快）
    memset(dist, 0x3f, sizeof dist);
    // 步骤2：定义小根堆，堆里存{距离, 结点编号}，堆顶是最小的
    priority_queue<PII, vector<PII>, greater<PII>> heap; 
    // 步骤3：把起点的{距离0, 起点s}放进堆里（初始化堆）
    heap.push({0, s});
    dist[s] = 0;  // 和常规版一样，起点到自己的距离是0
    
    // 步骤4：外层循环（只要堆里有元素就循环，代替常规版的n-1次循环）
    while(heap.size())
    {
        // 步骤5：取出堆顶的最小元素（距离最小的结点），并删掉堆顶
        auto t = heap.top(); heap.pop();
        int u = t.second;  // 堆里存的是{距离, 结点}，所以t.second是结点编号u
        
        // 步骤6：如果u已经标记过（最短路确定），直接跳过（堆里可能存重复的u）
        if(st[u]) continue;
        // 步骤7：给u打标记（和常规版一样，确定u的最短路）
        st[u] = true;
        
        // 步骤8：松弛操作（和常规版基本一样，多了一步把新距离放进堆）
        for(auto& t : edges[u])  // 遍历u能到的所有点
        {
            int v = t.first, w = t.second;  // v是终点，w是路长
            // 如果"起点到u的距离 + u到v的路长"比"原来的起点到v的距离"小
            if(dist[u] + w < dist[v])
            {
                dist[v] = dist[u] + w;  // 更新dist[v]（和常规版一样）
                // 新增：把更新后的{dist[v], v}放进堆里，方便后续找最小点
                heap.push({dist[v], v});
            }
        }
    }
    
    // 步骤9：输出结果（和常规版一样）
    for(int i = 1; i <= n; i++) cout << dist[i] << " ";
}

如果出现负权边，就会出错：

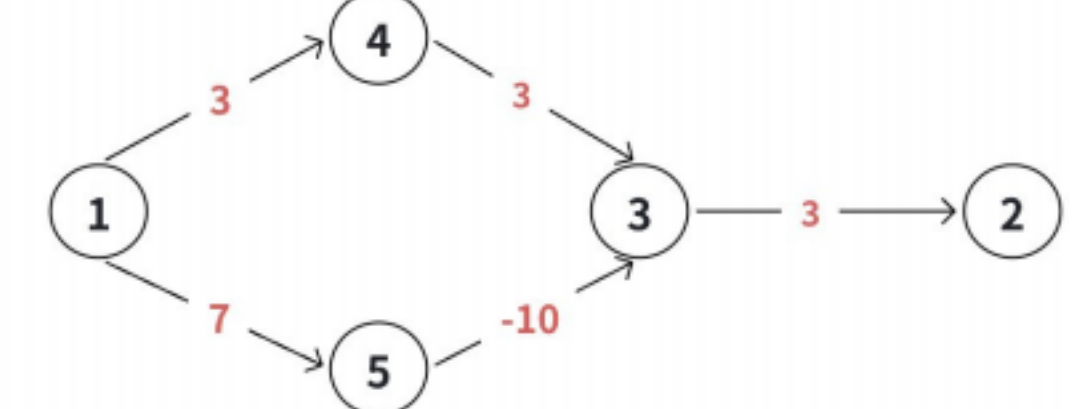
3 bellman-ford 算法

Bellman‒Ford 算法(之后简称 BF 算法)是⼀种基于松弛操作的最短路算法，可以求出有负权的图的最短路，并可以对最短路不存在的情况进⾏判断。
算法核⼼思想： 不断尝试对图上每⼀条边进⾏松弛，直到所有的点都⽆法松弛为⽌。

Bellman‒Ford 算法流程：
• 准备⼯作：
◦ 创建⼀个⻓度为 n 的 dist 数组，其中 dist[i] 表⽰从起点到 i 结点的最短路。
• 初始化： dist[1] = 0 ，其余结点的 dist 值为⽆穷⼤，表⽰还没有找到最短路。
• 重复：每次都对所有的边进⾏⼀次松弛操作。
• 重复上述操作，直到所有边都不需要松弛操作为⽌。

最多重复多少轮松弛操作？
在最短路存在的情况下，由于⼀次松弛操作会使最短路的边数⾄少增加 1，⽽最短路的边数最多为 n - 1。因此整个算法最多执⾏轮松弛操作 n - 1 轮。故总时间复杂度为 O ( nm ) 。

代码实现：

cpp 复制代码

#include <iostream>
#include <vector>
using namespace std;
typedef pair<int, int> PII;
const int N = 1e4 + 10, INF = 2147483647;
int n, m, s;
vector<PII> edges[N];
int dist[N];
void bf()
{
for(int i = 0; i <= n; i++) dist[i] = INF;
dist[s] = 0;
bool flag = false;
for(int i = 1; i < n; i++)
{
flag = false; // 判断是否进⾏了松弛操作
for(int u = 1; u <= n; u++)
{
if(dist[u] == INF) continue;
for(auto& t : edges[u])
{
int v = t.first, w = t.second;
if(dist[u] + w < dist[v])
{
dist[v] = dist[u] + w;
flag = true;
}
}
}
if(flag == false) break;
}
for(int i = 1; i <= n; i++) cout << dist[i] << " ";
}
int main()
{
cin >> n >> m >> s;
for(int i = 1; i <= m; i++)
{
int u, v, w; cin >> u >> v >> w;
edges[u].push_back({v, w});
}
bf();
return 0;
}

4 spfa 算法

spfa 即 Shortest Path Faster Algorithm，本质是⽤队列对 BF 算法做优化。
在 BF 算法中，很多时候我们并不需要那么多⽆⽤的松弛操作：
• 只有上⼀次被松弛的结点，它的出边，才有可能引起下⼀次的松弛操作；
• 因此，如果⽤队列来维护"哪些结点可能会引起松弛操作"，就能只访问必要的边了，时间复杂度就能降低。

spfa 算法流程：
• 准备⼯作： ◦ 创建⼀个⻓度为 n 的 dist 数组，其中 dist[i] 表⽰从起点到 i 结点的最短路；
◦ 创建⼀个⻓度为 n 的 bool 数组 st ，其中 st[i] 表⽰ i 点是否已经在队列中。
• 初始化：标记 dist[1] = 0 ，同时 1 ⼊队；其余结点的 dist 值为⽆穷⼤，表⽰还没有找到
最短路。
• 重复：每次拿出队头元素 u ，去掉在队列中的标记，同时对 u 所有相连的点 v 进⾏松弛操作。
如果结点 v 被松弛，那就放进队列中。
• 重复上述操作，直到队列中没有结点为⽌。

注意注意注意：
虽然在⼤多数情况下 spfa 跑得很快，但其最坏情况下的时间复杂度为。将其卡到这个复杂度
也是不难的，所以在没有负权边时最好使⽤ Dijkstra 算法。

cpp 复制代码

#include <iostream>
#include <queue>
#include <vector>
using namespace std;
typedef pair<int, int> PII;
const int N = 1e4 + 10, INF = 2147483647;
int n, m, s;
vector<PII> edges[N];
int dist[N];
bool st[N]; // 标记哪些结点在队列中
void spfa()
{
for(int i = 0; i <= n; i++) dist[i] = INF;
queue<int> q;
q.push(s);
dist[s] = 0;
st[s] = true;
while(q.size())
{
auto a = q.front(); q.pop();
st[a] = false;
for(auto& t : edges[a])
{
int b = t.first, c = t.second;
if(dist[a] + c < dist[b])
{
dist[b] = dist[a] + c;
if(!st[b])
{
q.push(b);
st[b] = true;
}
}
}
}
for(int i = 1; i <= n; i++) cout << dist[i] << " ";
}
int main()
{
cin >> n >> m >> s;
for(int i = 1; i <= m; i++)
{
int a, b, c; cin >> a >> b >> c;
edges[a].push_back({b, c});
}
spfa();
return 0;
}

5 【模板】单源最短路问题（弱化版）

题⽬来源：洛⾕
题⽬链接： P3371 【模板】单源最短路径（弱化版）
难度系数： ★★

题目背景

本题测试数据为随机数据，在考试中可能会出现构造数据让 SPFA 不通过，如有需要请移步 P4779。

题目描述

如题，给出一个有向图，请输出从某一点出发到所有点的最短路径长度。

输入格式

第一行包含三个整数 n,m,s，分别表示点的个数、有向边的个数、出发点的编号。

接下来 m 行每行包含三个整数 u,v,w，表示一条 u→v 的，长度为 w 的边。

输出格式

输出一行 n 个整数，第 i 个表示 s 到第 i 个点的最短路径，若不能到达则输出 231−1。

输入输出样例

输入 #1复制

复制代码

输出 #1复制

复制代码

0 2 4 3

说明/提示

【数据范围】

对于 20% 的数据：1≤n≤5，1≤m≤15；

对于 40% 的数据：1≤n≤100，1≤m≤104；

对于 70% 的数据：1≤n≤1000，1≤m≤105；

对于 100% 的数据：1≤n≤104，1≤m≤5×105，1≤u,v≤n，w≥0，∑w<231，保证数据随机。

Update 2022/07/29：两个点之间可能有多条边，敬请注意。

对于真正 100% 的数据，请移步 P4779。请注意，该题与本题数据范围略有不同。

样例说明：

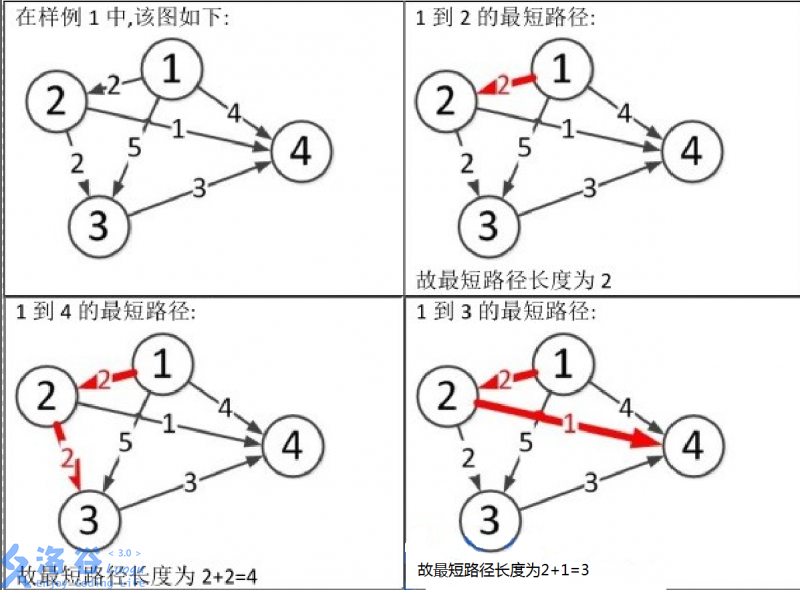
图片 1 到 3 和 1 到 4 的文字位置调换

【解法】

常规版 dijkstra 算法。

【参考代码】

cpp 复制代码

#include<iostream>
#include<vector>
#include<cmath>

using namespace std;
typedef pair<int,int>PII;  
typedef long long LL;
const int N=1e4+10,INF=2147483647;  // INF=2^31-1，符合题目要求
int n,m,s;
vector<PII>edges[N];  // 邻接表存图：edges[u]存<终点, 边权>

LL dist[N];  // 存起点到各点的最短距离
bool st[N];  // 标记是否确定最短路

void dijkstra(){
  
    for(int i=0;i<=n;i++) dist[i]=INF;
    dist[s]=0;  // 起点到自己的距离为0
    
    // 修正2：外层循环改为i=1到n-1（循环n-1次，常规版标准逻辑）
    for(int i=1;i<n;i++){
        // 步骤1：找未标记的点中距离最小的点u
        int u=0;
        for(int j=1;j<=n;j++){
            if(!st[j] && dist[j]<dist[u]){
                u=j;
            }
        }
        
        // 步骤2：标记u的最短路已确定
        st[u]=true;
        
        // 步骤3：松弛操作------用u更新邻接点的距离
        for(auto& t:edges[u]){
            int v=t.first, w=t.second;  // v=邻接点，w=边权
            if(dist[u]+w < dist[v]){
                dist[v] = dist[u]+w;
            }
        }
    }
    
    // 输出结果：起点到1~n号点的最短距离
    for(int i=1;i<=n;i++){
        cout<<dist[i]<<" ";
    }
}

int main()
{
    // 输入：结点数n、边数m、起点s
    cin>>n>>m>>s;
    // 输入m条有向边：u→v，权值w
    for(int i=1;i<=m;i++){
        int u,v,w;
        cin>>u>>v>>w;
        edges[u].push_back({v,w});
    }
    
    // 执行dijkstra算法并输出
    dijkstra();

    return 0;
}

6 【模板】单源最短路问题（标准版）

题⽬来源：洛⾕
题⽬链接： P4779 【模板】单源最短路径（标准版）
难度系数： ★★

题目背景

2018 年 7 月 19 日，某位同学在 NOI Day 1 T1 归程一题里非常熟练地使用了一个广为人知的算法求最短路。

然后呢？

100→60；

Ag→Cu；

最终，他因此没能与理想的大学达成契约。

小 F 衷心祝愿大家不再重蹈覆辙。

题目描述

给定一个 n 个点，m 条有向边的带非负权图，请你计算从 s 出发，到每个点的距离。

数据保证你能从 s 出发到任意点。

输入格式

第一行为三个正整数 n,m,s。第二行起 m 行，每行三个非负整数 ui,vi,wi，表示从 ui 到 vi 有一条权值为 wi 的有向边。

输出格式

输出一行 n 个空格分隔的非负整数，表示 s 到每个点的距离。

输入输出样例

输入 #1复制

复制代码

输出 #1复制

复制代码

0 2 4 3

说明/提示

样例解释请参考数据随机的模板题。

1≤n≤105；

1≤m≤2×105；

s=1；

1≤ui,vi≤n；

0≤wi≤109,

0≤∑wi≤109。

本题数据可能会持续更新，但不会重测，望周知。

2018.09.04 数据更新 from @zzq

【解法】

堆优化版 dj 算法。

【参考代码】

cpp 复制代码

#include <iostream>
#include <queue>
#include <vector>
#include <cstring>
using namespace std;

// PII：存<距离, 结点编号>，小根堆按距离从小到大排序
typedef pair<int, int> PII;
const int N = 1e5 + 10;  // 适配大数据量（1e5个点），比常规版的1e4更大
int n, m, s;             // n=结点数，m=边数，s=起点
vector<PII> edges[N];    // 邻接表：edges[u]存<终点v, 边权w>
bool st[N];              // 标记结点是否确定最短路
int dist[N];             // 存起点到各结点的最短距离

void dijkstra() {
    // 初始化dist数组为"无穷大"（0x3f≈10亿，足够大且不溢出）
    memset(dist, 0x3f, sizeof dist);
    // 定义小根堆：优先队列，greater<PII>表示按第一个元素升序排列
    priority_queue<PII, vector<PII>, greater<PII>> heap;
    
    // 起点初始化：距离为0，放入堆中
    heap.push({0, s});
    dist[s] = 0;
    
    // 堆不为空时循环（代替常规版的n-1次循环）
    while (heap.size()) {
        // 取出堆顶（距离最小的结点）并弹出
        auto t = heap.top();
        heap.pop();
        
        int u = t.second;  // 堆中存的是<距离, 结点>，所以t.second是结点编号
        if (st[u]) continue;  // 该结点已确定最短路，直接跳过（堆中可能有重复）
        st[u] = true;         // 标记u的最短路已确定
        
        // 松弛操作：遍历u的所有出边，更新邻接点的距离
        for (auto& edge : edges[u]) {
            int v = edge.first;  // 邻接点v
            int w = edge.second; // 边权w
            // 如果"起点到u的距离 + u到v的边权" < "起点到v的当前距离"，则更新
            if (dist[u] + w < dist[v]) {
                dist[v] = dist[u] + w;
                // 把更新后的<新距离, v>放入堆，供后续找最小距离
                heap.push({dist[v], v});
            }
        }
    }
    
    // 输出起点到1~n号点的最短距离
    for (int i = 1; i <= n; i++) {
        cout << dist[i] << " ";
    }
}

int main() {
    // 输入结点数、边数、起点
    cin >> n >> m >> s;
    // 输入m条有向边：u→v，权值w
    for (int i = 1; i <= m; i++) {
        int x, y, z;
        cin >> x >> y >> z;
        edges[x].push_back({y, z});
    }
    // 执行堆优化版dijkstra算法
    dijkstra();
    return 0;
}

7 【模板】负环

题⽬来源：洛⾕
题⽬链接： P3385 【模板】负环
难度系数： ★★
题目描述

给定一个 n 个点的有向图，请求出图中是否存在从顶点 1 出发能到达的负环。

负环的定义是：一条边权之和为负数的回路。

输入格式

本题单测试点有多组测试数据。

输入的第一行是一个整数 T，表示测试数据的组数。对于每组数据的格式如下：

第一行有两个整数，分别表示图的点数 n 和接下来给出边信息的条数 m。

接下来 m 行，每行三个整数 u,v,w。

若 w≥0，则表示存在一条从 u 至 v 边权为 w 的边，还存在一条从 v 至 u 边权为 w 的边。
若 w<0，则只表示存在一条从 u 至 v 边权为 w 的边。

输出格式

对于每组数据，输出一行一个字符串，若所求负环存在，则输出 YES，否则输出 NO。

输入输出样例

输入 #1复制

复制代码

输出 #1复制

复制代码

NO
YES

说明/提示

数据规模与约定

对于全部的测试点，保证：

1≤n≤2×103，1≤m≤3×103。
1≤u,v≤n，−104≤w≤104。
1≤T≤10。

提示

请注意，m 不是图的边数。

【解法】

如果图中存在负环，那么有可能不存在最短路。
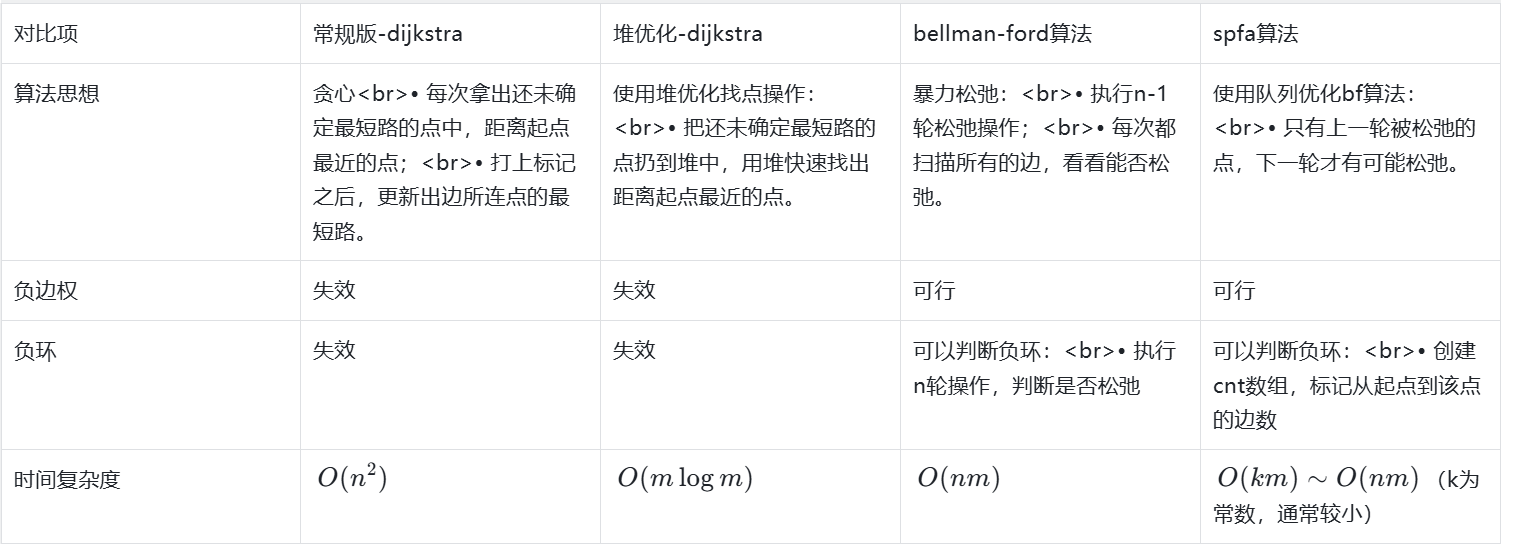
BF 算法判断负环
• 执⾏ n 轮松弛操作，如果第 n 轮还存在松弛操作，那么就有负环。
spfa 算法判断负环
• 维护⼀个 cnt 数组记录从起点到该点所经过的边数，如果 cnt[i] >= n ，说明有负环。

【参考代码】

BF 算法判断负环

cpp 复制代码

#include <iostream>
#include <cstring>
using namespace std;

const int N = 2e3 + 10;  // 最大点数（2000）
const int M = 3e3 + 10;  // 最大边数（3000），因为w≥0时边会翻倍，所以开2倍
int n, m;
int pos;  // 记录边的总数（因为w≥0时会加两条边）

// 结构体：存一条边的信息（起点u，终点v，边权w）
struct node {
    int u, v, w;
} e[M * 2];  // 边数组，开2倍防止溢出

int dist[N];  // dist[i]：从1号点到i号点的当前最短距离

// BF算法：返回true表示有负环，false表示没有
bool bf() {
    // 初始化距离：所有点设为"无穷大"（0x3f3f3f3f≈10亿），1号点距离为0
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    
    bool flag;  // 标记本轮是否有松弛操作（更新距离）
    // 核心：循环n轮（正常最短路最多n-1轮，第n轮还能更细就说明有负环）
    for (int i = 1; i <= n; i++) {
        flag = false;  // 初始化为无松弛
        // 遍历所有边，尝试松弛
        for (int j = 1; j <= pos; j++) {
            int u = e[j].u, v = e[j].v, w = e[j].w;
            // 如果u点的距离是无穷大（没走到过），跳过
            if (dist[u] == 0x3f3f3f3f) continue;
            // 松弛操作：如果从u到v能让dist[v]更小，就更新
            if (dist[u] + w < dist[v]) {
                dist[v] = dist[u] + w;
                flag = true;  // 标记本轮有松弛
            }
        }
        // 如果本轮没有松弛，说明所有最短路都确定了，直接返回false（无负环）
        if (!flag) return false;
    }
    // 循环n轮后还能松弛，说明有负环
    return flag;
}

int main() {
    int T;  // 测试数据组数
    cin >> T;
    while (T--) {  // 处理每组数据
        cin >> n >> m;
        pos = 0;  // 每组数据前清空边的计数
        
        // 输入m条边的信息，处理双向/单向
        for (int i = 1; i <= m; i++) {
            int u, v, w;
            cin >> u >> v >> w;
            // 先加u→v的边
            pos++;
            e[pos].u = u;
            e[pos].v = v;
            e[pos].w = w;
            // 如果w≥0，再加v→u的边（双向）
            if (w >= 0) {
                pos++;
                e[pos].u = v;
                e[pos].v = u;
                e[pos].w = w;
            }
        }
        
        // 调用BF算法，输出结果
        if (bf()) cout << "YES" << endl;
        else cout << "NO" << endl;
    }
    return 0;
}

spfa 算法判断负环

cpp 复制代码

// spfa 算法判断负环
#include <iostream>
#include <queue>
#include <vector>
#include <cstring>
using namespace std;
typedef pair<int, int> PII;
const int N = 2e3 + 10;
int n, m;
vector<PII> edges[N];
int dist[N];
bool st[N]; // 标记哪些点在队列中
int cnt[N];
bool spfa()
{
// 初始化
memset(dist, 0x3f, sizeof dist);
memset(st, 0, sizeof st);
memset(cnt, 0, sizeof cnt);
queue<int> q;
q.push(1);
dist[1] = 0;
st[1] = true;
while(q.size())
{
auto u = q.front(); q.pop();
st[u] = false;
for(auto& t : edges[u])
{
int v = t.first, w = t.second;
if(dist[u] + w < dist[v])
{
dist[v] = dist[u] + w;
cnt[v] = cnt[u] + 1;
if(cnt[v] >= n) return true;
if(!st[v])
{
q.push(v);
st[v] = true;
}
}
}
}
return false;
}
int main()
{
int T; cin >> T;
while(T--)
{
cin >> n >> m;
// 清空 edges 数组
for(int i = 1; i <= n; i++) edges[i].clear();
for(int i = 1; i <= m; i++)
{
int u, v, w; cin >> u >> v >> w;
edges[u].push_back({v, w});
if(w >= 0) edges[v].push_back({u, w});
}
if(spfa()) cout << "YES" << endl;
else cout << "NO" << endl;
}
return 0;
}

其实还有两个单源最短路算法，那就是普通 bfs 以及 01bfs：
• 普通 bfs 只能处理边权全部相同且⾮负的最短路；
• 01bfs 只能解决边权要么为 0，要么为 1 的情况。

.8 邮递员送信

题⽬来源：洛⾕
题⽬链接： P1629 邮递员送信
难度系数： ★★

题目描述

有一个邮递员要送东西，邮局在节点 1。他总共要送 n−1 样东西，其目的地分别是节点 2 到节点 n。由于这个城市的交通比较繁忙，因此所有的道路都是单行的，共有 m 条道路。这个邮递员每次只能带一样东西，并且运送每件物品过后必须返回邮局 。求送完这 n−1 样东西并且最终回到邮局最少需要的时间。

输入格式

第一行包括两个整数，n 和 m，表示城市的节点数量和道路数量。

第二行到第 (m+1) 行，每行三个整数，u,v,w，表示从 u 到 v 有一条通过时间为 w 的道路。

输出格式

输出仅一行，包含一个整数，为最少需要的时间。

输入输出样例

输入 #1复制

复制代码

输出 #1复制

复制代码

说明/提示

对于 30% 的数据，1≤n≤200。

对于 100% 的数据，1≤n≤103，1≤m≤105，1≤u,v≤n，1≤w≤104，输入保证任意两点都能互相到达。

【解法】

从起点找别的点的最短距离很简单，直接跑各种最短路算法均可。
但是从别的点回到起点的最短路，如果直接求时间复杂度巨⾼。思考⼀件事：
• 假设从某⼀点 z，到达起点的最短路径为：z -> y -> x -> s；
• 那么反过来就是 s -> x -> y -> z 的最短路径。
因此，仅需对原图的所有图建⽴⼀个"反图"，然后跑⼀遍最短路即可。这就是建"反图"的技巧。

【参考代码】

cpp 复制代码

#include <iostream>
#include <cstring>
using namespace std;

const int N = 1e3 + 10;  // 最大节点数（1000）
int n, m;
int e[N][N];  // 邻接矩阵存图：e[u][v]表示u→v的最短时间（初始为无穷大）
bool st[N];   // 标记节点是否确定最短路（dijkstra用）
int dist[N];  // 存起点（1号）到各点的最短距离

// 常规版dijkstra算法（邻接矩阵版）
void dijkstra() {
    // 初始化：距离设为无穷大，起点1的距离为0
    memset(dist, 0x3f, sizeof dist);
    memset(st, 0, sizeof st);  // 标记数组清零
    dist[1] = 0;
    
    // 循环n次，每次确定一个点的最短路
    for (int i = 1; i <= n; i++) {
        // 步骤1：找未标记的点中距离最小的点a
        int a = 0;
        for (int j = 1; j <= n; j++) {
            if (!st[j] && dist[j] < dist[a]) {
                a = j;
            }
        }
        st[a] = true;  // 标记a的最短路已确定
        
        // 步骤2：松弛操作------用a更新所有邻接点的距离
        for (int b = 1; b <= n; b++) {
            int c = e[a][b];  // a→b的时间
            // 如果"1→a的距离 + a→b的时间" < "1→b的当前距离"，更新
            if (dist[a] + c < dist[b]) {
                dist[b] = dist[a] + c;
            }
        }
    }
}

int main() {
    cin >> n >> m;
    
    // 初始化邻接矩阵：所有边设为无穷大（0x3f≈10亿）
    memset(e, 0x3f, sizeof e);
    
    // 输入m条单向边，存到邻接矩阵（保留最短的边，比如多条u→v取最小w）
    for (int i = 1; i <= m; i++) {
        int a, b, c;
        cin >> a >> b >> c;
        e[a][b] = min(c, e[a][b]);  // 防止重边，取最小的时间
    }
    
    // 第一步：跑原图的dijkstra，算1→z的最短时间（送过去）
    dijkstra();
    int ret = 0;
    for (int i = 1; i <= n; i++) {
        ret += dist[i];  // 累加1→2、1→3...1→n的时间
    }
    
    // 第二步：建反图（交换邻接矩阵的i和j，即边方向反过来）
    for (int i = 1; i <= n; i++) {
        for (int j = i + 1; j <= n; j++) {
            swap(e[i][j], e[j][i]);
        }
    }
    
    // 第三步：跑反图的dijkstra，算1→z的最短时间（等价于原图z→1的时间）
    dijkstra();
    for (int i = 1; i <= n; i++) {
        ret += dist[i];  // 累加2→1、3→1...n→1的时间
    }
    
    // 输出总时间
    cout << ret << endl;
    return 0;
}

9 采购特价商品

题⽬来源：洛⾕
题⽬链接： P1744 采购特价商品
难度系数： ★★

题目背景

《爱与愁的故事第三弹·shopping》第一章。

题目描述

中山路店山店海，成了购物狂爱与愁大神的"不归之路"。中山路上有 n（n≤100）家店，每家店的坐标均在 −10000 至 10000 之间。其中的 m 家店之间有通路。若有通路，则表示可以从一家店走到另一家店，通路的距离为两点间的直线距离。现在爱与愁大神要找出从一家店到另一家店之间的最短距离。你能帮爱与愁大神算出吗？

输入格式

共 n+m+3 行：

第一行：整数 n。

接下来 n 行：每行两个整数 x 和 y，描述了一家店的坐标。

接下来一行：整数 m。

接下来 m 行：每行描述一条通路，由两个整数 i 和 j 组成，表示第 i 家店和第 j 家店之间有通路。

接下来一行：两个整数 s 和 t，分别表示原点和目标店。

输出格式

仅一行：一个实数（保留两位小数），表示从 s 到 t 的最短路径长度。

输入输出样例

输入 #1复制

复制代码

输出 #1复制

复制代码

3.41

说明/提示

对于 100% 的数据：2≤n≤100，1≤i,j,s,t≤n，1≤m≤1000。

【解法】

看数据范围，所有的最短路算法均可解决，这⾥使⽤ BF 算法。
⽆需建图，只⽤把所有的边存下来。注意是⽆向边，所以要存两次，空间也要开两倍。
在所有边上做⼀次 bf 算法，输出结果即可。

【参考代码】

cpp 复制代码

#include <iostream>
#include <cmath>
#include <cstring>
using namespace std;

const int N = 110;   // 最多110家店（n≤100）
const int M = 1010;  // 最多1010条边（无向边存一次即可，BF里双向松弛）
int n, m, s, t;      // n=店数，m=通路数，s=起点，t=终点
double x[N], y[N];   // x[i]/y[i]：第i家店的坐标

// 结构体：存一条边的信息（a→b，距离c）
struct node {
    int a, b;        // a和b是店的编号
    double c;        // 通路的直线距离
} e[M];

// 计算第i家和第j家店的直线距离（勾股定理）
double calc(int i, int j) {
    double dx = x[i] - x[j];  // x坐标差
    double dy = y[i] - y[j];  // y坐标差
    return sqrt(dx * dx + dy * dy);  // 根号(x²+y²)
}

double dist[N];  // dist[i]：起点s到第i家店的最短距离

// BF算法：计算s到所有店的最短距离
void bf() {
    // 初始化：所有店的距离设为极大值（1e10），起点s的距离为0
    for (int i = 1; i <= n; i++) dist[i] = 1e10;
    dist[s] = 0;
    
    // 核心：循环n-1轮（最短路径最多经过n-1条边）
    for (int i = 1; i < n; i++) {
        // 遍历所有m条边，双向松弛（因为是无向边）
        for (int j = 1; j <= m; j++) {
            int a = e[j].a, b = e[j].b;
            double c = e[j].c;  // a和b之间的距离
            
            // 松弛1：a→b的方向
            if (dist[a] + c < dist[b]) {
                dist[b] = dist[a] + c;
            }
            // 松弛2：b→a的方向（无向边的核心）
            if (dist[b] + c < dist[a]) {
                dist[a] = dist[b] + c;
            }
        }
    }
}

int main() {
    // 第一步：输入n家店的坐标
    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> x[i] >> y[i];
    }
    
    // 第二步：输入m条通路，计算每条通路的距离
    cin >> m;
    for (int i = 1; i <= m; i++) {
        int a, b;
        cin >> a >> b;          // 第a家和第b家有通路
        e[i].a = a;
        e[i].b = b;
        e[i].c = calc(a, b);    // 计算a和b的直线距离
    }
    
    // 第三步：输入起点s和终点t
    cin >> s >> t;
    
    // 第四步：执行BF算法，计算最短距离
    bf();
    
    // 第五步：输出结果（保留两位小数）
    printf("%.2lf\n", dist[t]);
    return 0;
}

10 拉近距离

题⽬来源：洛⾕
题⽬链接： P2136 拉近距离
难度系数： ★★★

题目背景

我是源点，你是终点。我们之间有负权环。 ------小明

题目描述

在小明和小红的生活中，有 N 个关键的节点。有 M 个事件，记为一个三元组 (Si,Ti,Wi)，表示从节点 Si 有一个事件可以转移到 Ti，事件的效果就是使他们之间的距离减少 Wi。

这些节点构成了一个网络，其中节点 1 和 N 是特殊的，节点 1 代表小明，节点 N 代表小红，其他代表进展的阶段。所有事件可以自由选择是否进行，但每次只能进行当前节点邻接的。请你帮他们写一个程序，计算出他们之间可能的最短距离。

输入格式

第一行，两个正整数 N,M。

之后 M 行，每行 3 个空格隔开的整数 Si,Ti,Wi。

输出格式

一行，一个整数表示他们之间可能的最短距离。如果这个距离可以无限缩小，输出Forever love。

输入输出样例

输入 #1复制

复制代码

输出 #1复制

复制代码

-2

说明/提示

对于 20% 数据，N≤10，M≤50。

对于 50% 数据，N≤300，M≤5000。

对于 100% 数据，1≤N≤103，1≤M≤104，∣Wi∣≤100，保证从节点 1 到 2...N 有路径，从节点 N 到 1...N−1 有路径。

【解法】

bf 算法判断负环即可。但要注意⼀下细节：

题⽬中给的是距离 w 是能缩⼩的数，因此存边的时候，应该存成相反数；
爱情是双向奔赴的，我们要在 1->n 和 n->1 两种情况⾥⾯选择最⼩值。

【参考代码】

cpp 复制代码

#include<iostream>
#include<cstring>
using namespace std;

const int N=1e3+10, M=1e4+10;  // N=点数上限，M=边数上限
int n, m;                      // n=点数，m=边数

// 结构体：存一条有向边（a→b，边权c）
struct node {
    int a, b, c;
} e[M];

int dist[N];  // dist[i]：起点到i的最短距离

// BF算法：判断从起点s出发是否存在负环（返回true=有负环，false=无）
bool bf(int s) {
    // 初始化距离：所有点设为无穷大（0x3f3f3f3f≈10亿），起点s距离为0
    memset(dist, 0x3f, sizeof dist);
    dist[s] = 0;
    
    bool flag;  // 标记本轮是否有松弛操作
    // 循环n轮（正常最短路最多n-1轮，第n轮还能松弛→有负环）
    for(int i=1; i<=n; i++) {
        flag = false;  // 初始无松弛
        // 遍历所有边，尝试松弛
        for(int j=1; j<=m; j++) {
            int a = e[j].a, b = e[j].b, c = e[j].c;
            // 若a点未到达（距离无穷大），跳过
            if(dist[a] == 0x3f3f3f3f) continue;
            // 松弛操作：更新b点的最短距离
            if(dist[a] + c < dist[b]) {
                dist[b] = dist[a] + c;
                flag = true;  // 标记本轮有松弛
            }
        }
        // 本轮无松弛，说明无负环，直接返回false
        if(flag == false) return flag;
    }
    // 循环n轮后仍有松弛，说明有负环，返回true
    return flag;
}

int main() {
    cin >> n >> m;
    for(int i=1; i<=m; i++) {
        cin >> e[i].a >> e[i].b >> e[i].c;
        e[i].c = -e[i].c;  // 边权取反：最长路→最短路（负环对应原问题正环）
    }
    
    int ret;  // 存1→n的最短距离（取反前的最长距离）
    // 第一步：判断从1出发是否有负环
    bool st = bf(1);
    if(st) {
        cout << "Forever lover" << endl;  // 有负环→输出
        return 0;
    }
    ret = dist[n];  // 记录1→n的最短距离（取反后）
    
    // 第二步：判断从n出发是否有负环
    st = bf(n);
    if(st) {
        cout << "Forever lover" << endl;  
        return 0;
    }
    
    // 第三步：输出1→n和n→1的最短距离（取反后）的最小值
    cout << min(ret, dist[1]) << endl;

    return 0;
}