Performance boundary (LS)
数据矩阵:X∈RN×M,(N>M)X\in R^{N\times M},(N>M)X∈RN×M,(N>M)
权值:w∈RM\bold w\in \R^Mw∈RM
分析最小二乘的性能能够达到什么程度?
∥d−Xw∥2\|d-X\bold w\|^2∥d−Xw∥2
我们可以对XXX进行奇异值分解 :∥d−UTΣVw∥2=∥UTUd−UTΣVw∥2=∥UT(Ud−ΣVw)∥2=∥Ud−ΣVw∥2= =w~=Vwd~=Ud∥d~−Σw~∥2\begin{align*}\|d-U^T\Sigma V\bold w\|^2&=\|U^TUd-U^T\Sigma V\bold w\|^2\\&=\|U^T(Ud -\Sigma V\bold w)\|^2\\&=\|Ud -\Sigma V\bold w\|^2\\&\overset{\tilde d=Ud}{\underset{\tilde {\bold w}=V\bold w}{=\!=}}\|\tilde d-\Sigma \tilde{\bold w} \|^2\end{align*}∥d−UTΣVw∥2=∥UTUd−UTΣVw∥2=∥UT(Ud−ΣVw)∥2=∥Ud−ΣVw∥2w~=Vw==d~=Ud∥d~−Σw~∥2
假定 Σ=[Λ0],Λ=diag(λ1,...,λM)\Sigma=\begin{bmatrix}\Lambda \\\bold 0\end{bmatrix}, \Lambda=\text{diag}(\lambda_1,...,\lambda_M)Σ=[Λ0],Λ=diag(λ1,...,λM)
∥d~−Σw~∥2=∥d~−[Λ0]w~∥2=∥[d~(1)−Λw~d~(2)−0]∥2=∥d~(1)−Λw~∥2+∥d~(2)∥2\begin{align*}\|\tilde d-\Sigma \tilde{\bold w} \|^2&=\|\tilde d-\begin{bmatrix}\Lambda \\\bold 0\end{bmatrix} \tilde{\bold w} \|^2\\&=\|\begin{bmatrix}\tilde d^{(1)}-\Lambda\tilde {\bold w}\\\tilde d^{(2)}-\bold 0\end{bmatrix}\|^2\\&=\|\tilde d^{(1)}-\Lambda\tilde {\bold w}\|^2+\|\tilde d^{(2)}\|^2\end{align*}∥d~−Σw~∥2=∥d~−[Λ0]w~∥2=∥[d~(1)−Λw~d~(2)−0]∥2=∥d~(1)−Λw~∥2+∥d~(2)∥2
固然,我可以让 w~=Λ−1d~(1)\tilde{\bold w}=\Lambda^{-1}\tilde d^{(1)}w~=Λ−1d~(1) 来让第一个分量为零。
然而,第二个分量和滤波器系数没有一毛钱关系,这一部分残差就是最小二乘的性能边界(一方面取决于目标 ddd,另一方面取决于数据矩阵 XXX 奇异值分解的结果)。
下面换一个角度看性能边界:QR分解
数据矩阵:X=QR,QQT=QTQ=IX=QR,QQ^T=Q^TQ=IX=QR,QQT=QTQ=I
R=[Λu0](Λu:Upper Triangular Matrix)R=\begin{bmatrix}\Lambda_{u}\\\bold 0\end{bmatrix}(\Lambda_u:\text{Upper Triangular Matrix})R=[Λu0](Λu:Upper Triangular Matrix)
∥d−Xw∥2=∥d−QRw∥2=∥QQTd−QRw∥2=∥Q(QTd−Rw)∥2=∥QTd−Rw∥2= =d~=QTd∥d~−Rw∥2=∥[d~(1)−Λuwd~(2)−0]∥2=∥d~(1)−Λuw∥2+∥d~(2)∥2\begin{align*}\|d-X\bold w\|^2&=\|d-QR\bold w\|^2\\&=\|QQ^Td-QR\bold w\|^2\\&=\|Q(Q^Td-R\bold w)\|^2\\&=\|Q^Td-R\bold w\|^2\\&\overset{\tilde d=Q^Td}{{=\!=}}\|\tilde d-R \bold w\|^2\\&=\|\begin{bmatrix}\tilde d^{(1)}-\Lambda_u{\bold w}\\\tilde d^{(2)}-\bold 0\end{bmatrix}\|^2\\&=\|\tilde d^{(1)}-\Lambda_u{\bold w}\|^2+\|\tilde d^{(2)}\|^2\end{align*}∥d−Xw∥2=∥d−QRw∥2=∥QQTd−QRw∥2=∥Q(QTd−Rw)∥2=∥QTd−Rw∥2==d~=QTd∥d~−Rw∥2=∥[d~(1)−Λuwd~(2)−0]∥2=∥d~(1)−Λuw∥2+∥d~(2)∥2
我们得到了跟奇异值分解一样的结论。
下面我们谈QR分解的线性代数技术,这有助于我们构造全新的自适应方法。
我们的目标是找到一个能够把数据矩阵 XXX 上三角化的正交变换:QTX=[Λu0](Λu:Upper Triangular Matrix)Q^TX=\begin{bmatrix}\Lambda_{u}\\\bold 0\end{bmatrix}(\Lambda_u:\text{Upper Triangular Matrix})QTX=[Λu0](Λu:Upper Triangular Matrix)
正交变换是刚体变换的一种,而刚体变换就三种类型:平移、旋转(rotation)、反射(reflection)。
下面我们先谈反射:
1. Householder Reflection

假设轴的正交补空间为 u∈RM,∥u∥2=1u\in R^M,\|u\|^2=1u∈RM,∥u∥2=1
ProjuX=u(uTu)−1uTX=uuTX\text{Proj}_uX=u(u^Tu)^{-1}u^TX=uu^TXProjuX=u(uTu)−1uTX=uuTX
得到 XXX 的反射结果:X−2uuTX=(I−2uuT)XX-2uu^TX=(I-2uu^T)XX−2uuTX=(I−2uuT)X
人们把矩阵 H=I−2uuTH=I-2uu^TH=I−2uuT叫 Householder。
性质:
- H=HTH=H^TH=HT
- HHT=IHH^T=IHHT=I
可见 HHH 是个正交阵。
现在假如我有一个目标 X~\tilde XX~,我就可以根据 u=X−X~⇒u=u/∥u∥u=X-\tilde X\Rightarrow u=u/\|u\|u=X−X~⇒u=u/∥u∥得到反射矩阵 H=I−2uuTH=I-2uu^TH=I−2uuT
下面我们来说明 HHH 就是我感兴趣的正交矩阵 QQQ。
-
首先看 XXX 的第一列:
经过反射变换后只剩下上三角第一列的第一个元素:
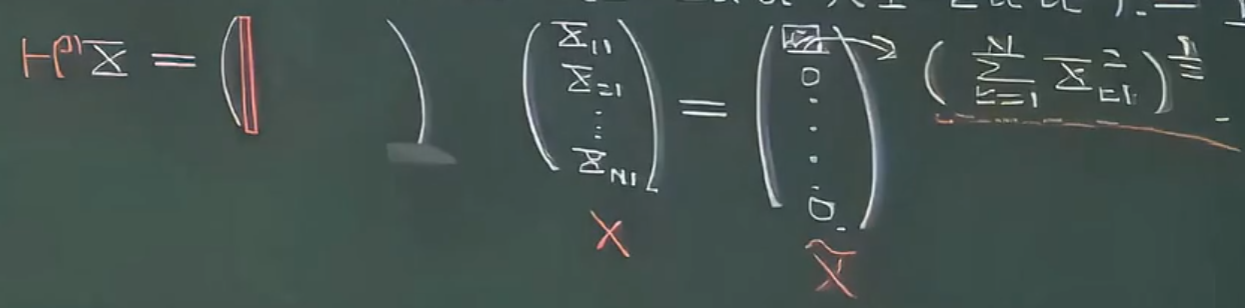
因为反射不改变模长,所以上三角矩阵的第一列的第一个元素为:(∑k=1Nxk12)12(\sum_{k=1}^Nx_{k1}^2)^{\frac{1}{2}}(∑k=1Nxk12)21
-
再看 XXX 的第二列:
在处理第二列的时候,我其实并不关心第一个元素,因为第二列第一个元素经过反射后处于 RRR 矩阵的第一行,而 RRR 只有上三角不为零,所以事实上我只关心如何把下头的部分变为零。于是在线性代数中,就可以用这么一个分块矩阵(也是正交阵)来作用在 XXX 上:
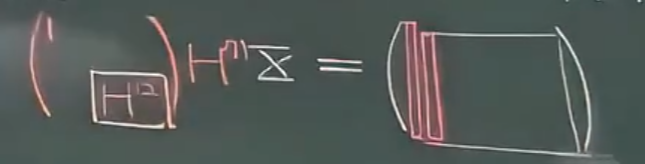
-
XXX 的后几列依旧可以按相同的故事书写:

-
一共反射 MMM 列: H=[IM−1×M−1HM]⋅⋅⋅[I3×3H4][I2×2H3][1H2]H(1)H=\begin{bmatrix}I_{M-1\times M-1}&\\&H^{M}\end{bmatrix}···\begin{bmatrix}I_{3\times 3}&\\&H^{4}\end{bmatrix}\begin{bmatrix}I_{2\times 2}&\\&H^{3}\end{bmatrix}\begin{bmatrix}1&\\&H^{2}\end{bmatrix}H^{(1)}H=[IM−1×M−1HM]⋅⋅⋅[I3×3H4][I2×2H3][1H2]H(1)
于是QR分解就这样做好了。
2. Givens Rotation
我们再来介绍另一种基于旋转的正交变换技巧:Givens Rotation
首先它是针对两维矢量而言的:[x1x2]→[(x12+x22)120]=[cosθsinθ−sinθcosθ][x1x2]\begin{bmatrix}x_1\\x_2\end{bmatrix}\to\begin{bmatrix}(x_1^2+x_2^2)^{\frac{1}{2}}\\0\end{bmatrix}=\begin{bmatrix}\cos\theta&\sin\theta\\-\sin\theta&\cos\theta\end{bmatrix}\begin{bmatrix}x_1\\x_2\end{bmatrix}[x1x2]→[(x12+x22)210]=[cosθ−sinθsinθcosθ][x1x2]
于是:⇒−x1sinθ+x2cosθ=0⇒θ=tan−1(x2x1)\Rightarrow -x_1 \sin\theta+x_2 \cos\theta=0\Rightarrow\theta=\tan^{-1}(\frac{x_2}{x_1})⇒−x1sinθ+x2cosθ=0⇒θ=tan−1(x1x2)
- 对于数据矩阵的第一列来说:
我们的目标首先放在第一列的第二个元素上,我希望把它搞成零,那么只需要构造如下右边的一个矩阵就行了(如果说Household像机关枪,一扫一大片,那么Given就有点像狙击枪,每次只打一个)
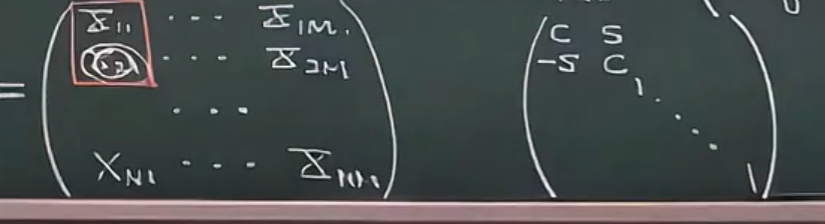
- 再看数据矩阵第一列的第三个目标:
为了构造两维矢量,只需要把第一列的第三个元素和第一个元素组起来就行了,对应的旋转矩阵见下面第三个矩阵(第二行中间的1确保了不改变数据矩阵的第二行)
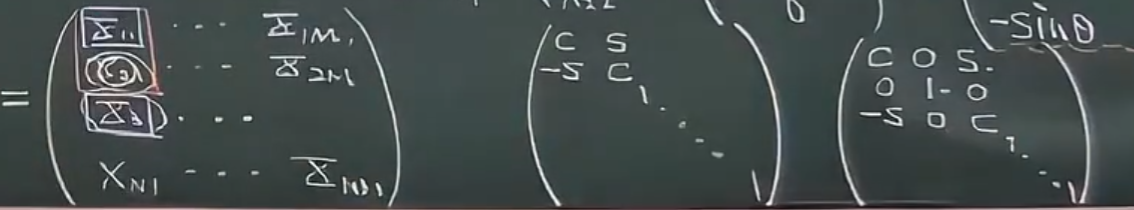
- 以此类推,到了第二列的时候:
只需要像这样构造旋转矩阵即可接续类似的故事。
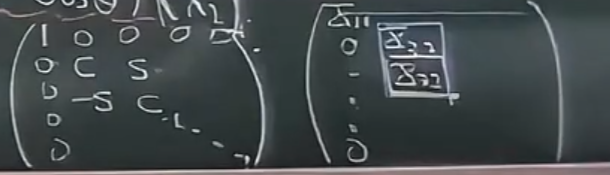
由此完成由正交矩阵把数据矩阵变成上三角。
RLS自适应
回顾递归最小二乘(RLS):
- Xn+1=[Xnxn+1]X_{n+1}=\begin{bmatrix}X_n\\x_{n+1}\end{bmatrix}Xn+1=[Xnxn+1]
- (Xn+1TXn+1)−1=(XnTXn+xn+1Txn+1)−1(X_{n+1}^TX_{n+1})^{-1}=(X_n^TX_n+x^T_{n+1}x_{n+1})^{-1}(Xn+1TXn+1)−1=(XnTXn+xn+1Txn+1)−1
现在从QR分解的角度看自适应:Rn→Rn+1R_n\to R_{n+1}Rn→Rn+1
QnT1\]\[Xnxn+1\]=\[Rnxn+1\]=\[Λn0xn+1\]\\begin{bmatrix}Q\^T_n\&\\\\\&1\\end{bmatrix}\\begin{bmatrix}X_n\\\\x_{n+1}\\end{bmatrix}=\\begin{bmatrix}R_n\\\\x_{n+1}\\end{bmatrix}=\\begin{bmatrix}\\Lambda_n\\\\\\bold0\\\\x_{n+1}\\end{bmatrix}\[QnT1\]\[Xnxn+1\]=\[Rnxn+1\]= Λn0xn+1 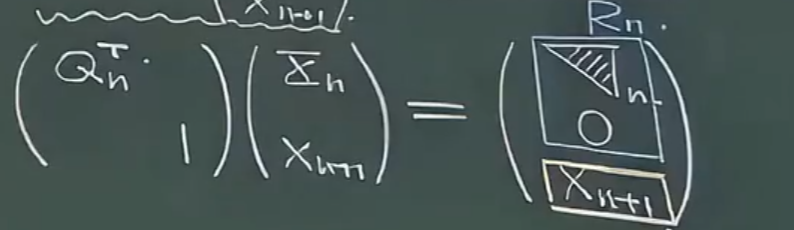 为了将下头的 xn+1x_{n+1}xn+1 全部搞成零,采取的策略是 GIvens 旋转(因为Householder列消除的方式会造成大面积浪费) 于是,故事结束了。基于Givens旋转的递归最小二乘也就是设备里采用的技术CORDIC (FPGA)\\text{CORDIC (FPGA)}CORDIC (FPGA)。数据进到存储器后是**原位操作(Inplace Computation)**