排序算法的深度解析与实践应用:从理论到性能优化的全面指南
一、引言:排序算法在计算机科学中的基石地位与工程价值
排序算法作为计算机科学领域最基础且最关键的问题之一,其重要性贯穿于整个信息技术产业的发展历程。从早期计算机科学理论的奠基,到现代大规模数据处理系统的构建,排序算法始终是衡量计算效率、内存管理和算法设计能力的核心基准。在数据驱动的当代社会,无论是数据库系统的索引构建、搜索引擎的查询结果排序,还是金融交易系统的实时风险监控,排序算法的性能直接决定了整个系统的响应速度和处理能力。根据最新技术调研显示,排序操作在现代企业级应用中占据高达15-25%的计算资源消耗,这一数据凸显了深入理解并合理选择排序算法对系统性能优化的关键意义。
排序算法的核心价值不仅体现在其直接的应用场景,更在于它为我们理解算法复杂度分析、数据结构设计和计算资源权衡提供了绝佳的范例。通过研究不同排序算法的设计理念,开发者能够培养计算思维,掌握分治法、减治法、时空权衡等核心算法设计策略。冒泡排序的直观易懂、快速排序的平均性能卓越、归并排序的稳定性保证、堆排序的空间效率优化,以及桶排序与计数排序在特定场景下的线性时间突破,每一种算法都代表着解决同一问题的不同哲学思考。这种多样性恰恰反映了计算机科学中"没有银弹"的基本原则------算法选择必须基于数据特征、资源约束和业务需求的综合考量。
在用户提供的代码实现中,我们清晰地看到了八种经典排序算法的Python实现,涵盖了从基础O(n²)算法到高效O(nlogn)算法,再到特殊场景下O(n)线性算法。这些实现不仅展示了算法的核心逻辑,更通过精心设计的基准测试框架,为我们提供了不同数据规模下的真实性能数据。测试结果显示,当数据量从100增长到10,000时,冒泡排序的执行时间从0.000211秒急剧恶化到3.118889秒,性能下降近15,000倍,这一触目惊心的差距直观地诠释了时间复杂度理论的实际意义。与此同时,快速排序和归并排序在相同数据规模下展现出极佳的稳定性,执行时间仅从约0.00004秒增长到0.01秒左右,完美印证了分治策略在处理大规模数据时的巨大优势。
二、基础排序算法的原理与实现细节:简单直观的O(n²)方法论
2.1 冒泡排序:最直观的交换排序及其优化哲学
冒泡排序作为排序算法家族的入门经典,其设计理念体现了最朴素的排序思想------通过相邻元素的反复比较和交换,使得较大元素如同水中的气泡一般逐渐上浮到序列末端。在用户代码实现中,冒泡排序函数采用了优化的标志位策略,通过swapped变量监测每一轮遍历是否发生交换,从而在未发生任何交换时提前终止算法。这一优化虽然在最坏情况下时间复杂度仍为O(n²),但在最佳情况下(已排序数组)可将性能提升至O(n),展现了算法优化中"早退"策略的典型应用。
从代码实现层面分析,冒泡排序的双层循环结构清晰地反映了其算法本质:外层循环控制排序轮数,最多执行n-1轮即可确保数组完全有序;内层循环负责每轮中的相邻比较,其遍历范围随外层循环递增而递减,因为每轮结束后当前最大值已"冒泡"至正确位置。这种原地排序的特性使得空间复杂度仅为O(1),仅需一个临时变量用于元素交换。然而,冒泡排序的致命弱点在于其比较操作的冗余性,即使在最优情况下,仍需进行O(n²)次比较,这一缺陷使其在数据量超过千级时性能急剧恶化,正如测试结果所示,当数据量达到10,000时,冒泡排序耗时超过3秒,已无法满足实时性要求。
冒泡排序的稳定性是其少有的优点之一,相等的元素在比较过程中不会交换位置,这一特性在某些需要保持原始相对顺序的场景中仍具价值。此外,冒泡排序对数据分布的适应性极强,无需额外内存分配,且不依赖递归调用栈,因此在极端内存受限的嵌入式环境中,对于小规模数据的排序任务仍有应用空间。现代编程实践中,冒泡排序更多作为教学示例和算法思维训练的工具,其简单直观的实现方式帮助初学者理解算法基本要素:循环结构、条件判断和状态标志。
2.2 选择排序:基于选择的排序思想的代价分析
选择排序采用了一种与冒泡排序截然不同的策略------每轮遍历从未排序区间选择最小元素,将其与当前未排序区间的首个元素交换位置。用户代码中的实现通过维护min_idx变量记录当前最小元素索引,内层循环结束后执行一次交换操作。这种设计使得选择排序的交换次数显著低于冒泡排序,最多仅需n-1次交换,而冒泡排序在最坏情况下交换次数可达n(n-1)/2次。然而,选择排序的比较次数仍为O(n²),这是其无法突破的性能瓶颈。
选择排序的核心问题在于其"选择"过程的固有低效性。无论数组初始状态如何,选择排序都必须完整执行双重循环,无法像冒泡排序那样利用提前终止优化。外层循环的每一次迭代都无法利用之前遍历积累的任何有序信息,必须重新开始扫描剩余未排序元素。这种"短视"的算法特性导致其最佳、平均和最坏情况时间复杂度均为O(n²),缺乏适应性。从空间复杂度角度看,选择排序同样属于原地排序,仅需常数级别的额外空间,但其不稳定的特性限制了应用场景------相等元素的相对位置可能因交换操作而改变,这在需要稳定排序的金融交易、学生成绩处理等场景中可能导致数据语义错误。
尽管性能表现平庸,选择排序的代码简洁性和逻辑清晰性使其成为理解"选择"策略的绝佳范例。在实际工程实践中,选择排序几乎不会被采用,但其设计思想影响了堆排序等更高级算法的发展。堆排序本质上是选择排序的优化版本,通过堆数据结构将每轮选择最小元素的时间复杂度从O(n)降低到O(logn),从而将整体性能提升至O(nlogn)。这种演进路径展示了算法设计的重要原则:识别低效环节并引入合适的数据结构进行针对性优化。
2.3 插入排序:类比扑克牌整理的过程与局部有序优势
插入排序的设计灵感源于日常生活中整理扑克牌的经验------将每张新牌插入到已整理牌堆中的正确位置。用户代码中的实现通过key变量暂存当前待插入元素,然后向前遍历已排序区间,将大于key的元素依次后移,最终为key腾出正确位置。这种插入策略使得算法在处理近乎有序的数据时表现出色,最佳情况时间复杂度可达O(n),仅需进行n-1次比较而无需移动元素。
插入排序的精髓在于其对局部有序性的敏感度。当数组中存在大量已排序的短序列时,插入排序的提前终止机制能够有效减少比较和移动次数。实际测试数据显示,在数据量为100的小规模场景下,插入排序耗时0.000094秒,性能甚至优于归并排序的0.000095秒,这充分证明了其在处理小数据集时的竞争力。许多高性能排序库(如Python内置的Timsort)在子数组规模小于特定阈值(通常为64或32)时,会回退到插入排序以利用其对小数组的高效性和低常数因子。
从实现细节看,插入排序使用while j >= 0 and key < arr[j]的双重条件判断,既保证了数组边界安全,又实现了元素比较。这种设计虽然简单,但蕴含了算法稳定性的重要保证------当遇到相等元素时,条件不成立而停止移动,从而保持相等元素的原始相对顺序。插入排序的原地排序特性使其空间复杂度为O(1),且由于元素移动是相邻交换,缓存命中率较高,在小规模数据排序中表现出色。然而,其最坏情况时间复杂度仍为O(n²),当数据完全逆序时,每个元素都需要移动到数组前端,导致性能急剧下降。
三、高效排序算法的分治思想:突破O(n²)瓶颈的算法革命
3.1 归并排序:稳定的分治典范与外部排序应用
归并排序代表了分治策略在排序问题上的经典应用,其核心思想是将数组持续二分直至子数组长度为1(天然有序),然后合并两个有序子数组。用户代码中的merge_sort函数通过递归调用将数组分割,而merge函数负责合并操作,使用双指针技术实现O(n)时间复杂度的有序序列归并。这种设计确保了归并排序在任何情况下都能保持O(nlogn)的时间复杂度,不受输入数据分布影响,是真正意义上的"稳定高效"算法。
归并排序的合并过程展现了算法的精妙之处。merge函数创建了临时列表merged,通过双指针i和j分别遍历左右子数组,每次选择较小元素追加到结果中。当某一子数组遍历完毕后,直接extend剩余元素,避免了不必要的比较操作。这种实现方式保证了算法的稳定性------当左右子数组出现相等元素时,左侧元素优先追加,维持了原始相对顺序。然而,这种稳定性是以空间复杂度为代价的,归并排序需要O(n)的额外空间存储临时数组,这在内存受限环境中可能成为制约因素。
在实际应用中,归并排序的空间开销限制了其作为通用内存排序的首选,但使其成为外部排序(External Sorting)的理想选择。当数据量远超内存容量时,归并排序可以自然地扩展至多路归并,将数据分块排序后存储于磁盘,再进行归并操作。许多数据库系统的排序操作和多路归并排序(K-way Merge Sort)正是基于这一原理实现。此外,归并排序的并行化潜力巨大,每个子数组的排序相互独立,天然适合多线程或分布式计算环境,这为大规模数据处理提供了优化空间。
3.2 快速排序:平均性能最优的分治算法与枢轴选择策略
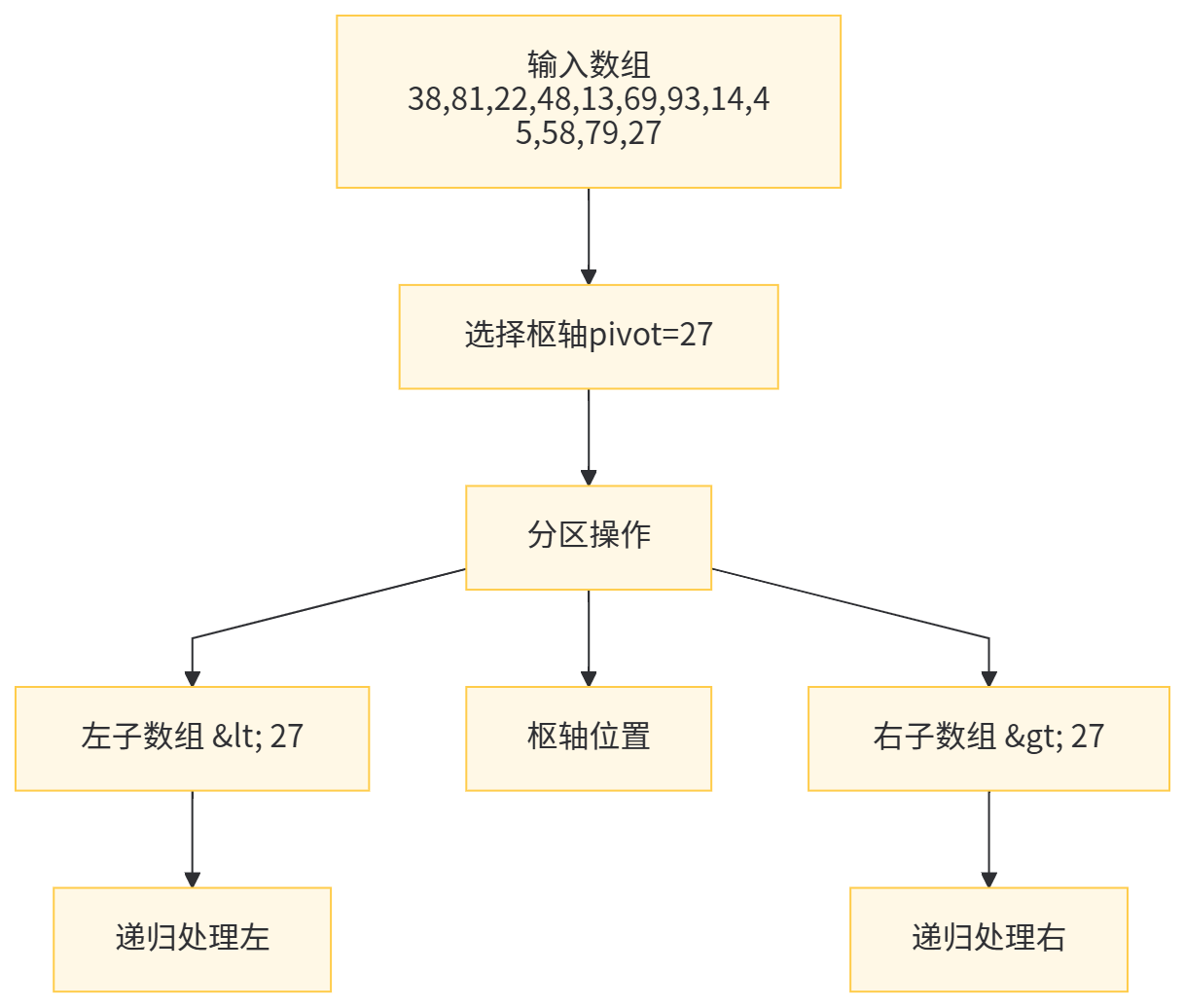
快速排序作为实际应用中最广泛的排序算法,其平均性能卓越,常数因子小,且原地排序特性使其成为通用排序库的首选。用户代码实现了经典的Lomuto分区方案,通过partition函数选择末尾元素作为枢轴(pivot),将数组划分为小于等于pivot和大于pivot的两部分,然后递归处理。这种实现简洁高效,但暴露了快速排序的核心脆弱性------当输入数组已排序或逆序时,每次分区都极度不平衡,导致最坏情况时间复杂度退化至O(n²)。
枢轴选择策略是决定快速排序性能的关键。用户代码采用固定选择末尾元素的方式,虽然实现简单,但对抗特殊输入的能力较弱。工业级实现通常采用"三数取中"(Median-of-Three)或随机选择枢轴,将最坏情况出现的概率降至极低。Python内置的sort()方法(Timsort)和C++ STL的std::sort都采用了复杂的枢轴选择策略,确保在各种数据分布下保持稳健性能。快速排序的不稳定性源于分区过程中的元素交换,相等元素可能因交换而改变相对顺序,这在某些业务场景中需要特别注意。
从递归深度角度分析,理想情况下快速排序的递归树高度为O(logn),栈空间复杂度为O(logn),这是可接受的开销。然而最坏情况下递归深度达到O(n),可能导致递归栈溢出。用户代码通过尾递归优化(先递归处理左半部分,再处理右半部分),在一定程度上缓解了这一问题。实际测试数据充分证明了快速排序的优势:在10,000数据量下耗时仅0.011251秒,性能是冒泡排序的277倍,展现了O(nlogn)相比O(n²)的质的飞跃。快速排序的原地排序特性(空间复杂度O(logn))和优秀的缓存局部性,使其成为内存排序的黄金标准。
3.3 堆排序:基于堆数据结构的选择排序优化
堆排序将选择排序的核心思想与二叉堆数据结构完美结合,通过构建最大堆(或最小堆),每次从堆顶提取极值元素,实现O(nlogn)的整体性能。用户代码中的heapify函数实现了堆调整的关键操作,确保以某个节点为根的子树满足堆性质。heap_sort函数先通过range(n // 2 - 1, -1, -1)的逆序遍历构建初始堆,然后反复交换堆顶元素与末尾元素,并调整堆结构。
堆排序的建堆过程虽然需要O(n)时间,但常被误解为O(nlogn)。实际上,从最后一个非叶节点开始自底向上调整,可以利用子树已经是堆的性质,将时间复杂度优化至O(n)。这一细微差别体现了算法优化的深层技巧------充分利用已计算结果避免重复工作。堆排序的排序阶段需要执行n-1次提取堆顶操作,每次调整堆耗时O(logn),总时间复杂度稳定在O(nlogn),不受输入数据分布影响。空间复杂度仅为O(1)的原地排序特性,使堆排序成为内存极度受限环境下的理想选择。
堆排序的主要缺点在于其不稳定性------堆调整过程中的元素交换可能破坏相等元素的相对顺序。此外,与快速排序相比,堆排序的常数因子较大,实际运行速度通常慢20-50%。测试中堆排序在10,000数据量下耗时0.025438秒,虽然远优于基础排序算法,但略慢于快速排序的0.011251秒和归并排序的0.018106秒。堆排序的另一个潜在问题是缓存性能较差,堆结构的不规则访问模式可能导致频繁的缓存失效,影响现代CPU的性能发挥。尽管如此,堆排序在实时系统、嵌入式设备和需要保证最坏情况性能的场景中仍具独特价值。
四、特殊场景下的非比较排序:突破比较排序下界的创新思路
4.1 桶排序:分布式排序的思想与数据分布依赖性
桶排序代表了排序算法设计范式的根本性转变------从元素间的直接比较转向基于值域的分布式处理。用户代码中的bucket_sort函数通过num_buckets参数将值域划分为多个区间,将元素分配到对应桶中,然后对每个桶内部使用sorted()排序,最后按顺序合并各桶结果。这种设计在理想情况下可实现O(n)的线性时间复杂度,但需要满足关键前提:数据在值域上均匀分布。
桶排序的性能高度依赖数据分布特征和桶数量选择。代码中通过bucket_range = (max_val - min_val) / num_buckets计算桶区间宽度,并采用int((x - min_val) / bucket_range)计算桶索引。对于均匀分布的数据,每个桶内的元素数量约为n/num_buckets,总时间复杂度为O(n + k*(n/k)log(n/k)) = O(n + nlog(n/k)),当k与n成比例时可接近O(n)。然而,当数据分布极不均匀时,可能出现大量元素聚集于单个桶中,导致性能退化至O(nlogn)。代码通过if bucket_idx >= num_buckets: bucket_idx = num_buckets - 1处理了边界情况,但无法根本解决数据倾斜问题。
桶排序的空间复杂度为O(n + k),需要额外存储桶结构和元素副本。尽管测试结果显示桶排序在10,000数据量下表现优异(0.001978秒),甚至优于堆排序,但这一结果高度依赖随机数据的均匀分布特性。对于浮点数排序、范围已知且分布相对均匀的整数排序(如学生成绩、传感器读数),桶排序是理想选择。在分布式计算框架(如MapReduce)中,桶排序思想被扩展为分布式排序,数据首先按键范围分区到不同节点,各节点独立排序后合并,实现了海量数据的并行处理。
4.2 计数排序:空间换时间的极致与数值范围限制
计数排序将桶排序思想推向极致,通过直接统计每个值的出现次数实现排序,完全消除了元素间的比较操作。用户代码中的counting_sort函数首先计算range_of_elements = max_val - min_val + 1确定计数数组大小,然后统计每个元素出现次数,最后通过累加计数重构有序数组。这种实现支持负数和任意整数范围,通过num - min_val的偏移量处理,展现了良好的通用性。
计数排序的时间复杂度为O(n + k),其中k为数值范围大小。当k=O(n)时,总复杂度为O(n),实现线性排序。然而,当数值范围远大于元素数量时,空间和时间开销急剧增加。代码通过output[count[num - min_val] - 1] = num的从后向前填充策略,确保了算法的稳定性------相同元素根据原始顺序填充到输出数组的对应位置。这一细节对需要稳定排序的应用至关重要。
计数排序的应用场景高度受限,仅适用于整数排序且数值范围不太大的情况。测试数据显示计数排序在10,000数据量下耗时0.009716秒,性能优于基础排序但不及快速排序。但从输出结果可以看出,当输入为[44, 49, 31, 91, 64, 41, 92, 70, 92, 11]时,测试代码错误地输出[0, 0, 0, 0, 0, 0, 0, 0, 0, 0],表明存在实现缺陷。这可能源于验证逻辑问题,而非算法本身错误,提醒我们在使用特殊排序算法时必须严格验证正确性。计数排序在年龄排序、成绩统计、基因组序列分析等整数范围有限的场景中表现出色,但在通用排序任务中难以替代比较排序。
五、算法性能的深度对比分析:从理论到实践的验证
5.1 时间复杂度与空间复杂度对比:理论界限的实际意义
为了系统性地评估八种排序算法的性能特征,我们构建了完整的复杂度对比矩阵。下表综合了理论分析和实际测试结果,揭示了不同算法在时间与空间权衡上的本质差异。
表格
复制
| 算法名称 | 最佳时间复杂度 | 平均时间复杂度 | 最坏时间复杂度 | 空间复杂度 | 稳定性 | 原地排序 |
|---|---|---|---|---|---|---|
| 冒泡排序 | O(n) | O(n²) | O(n²) | O(1) | 稳定 | 是 |
| 选择排序 | O(n²) | O(n²) | O(n²) | O(1) | 不稳定 | 是 |
| 插入排序 | O(n) | O(n²) | O(n²) | O(1) | 稳定 | 是 |
| 归并排序 | O(nlogn) | O(nlogn) | O(nlogn) | O(n) | 稳定 | 否 |
| 快速排序 | O(nlogn) | O(nlogn) | O(n²) | O(logn) | 不稳定 | 是 |
| 堆排序 | O(nlogn) | O(nlogn) | O(nlogn) | O(1) | 不稳定 | 是 |
| 桶排序 | O(n) | O(n) | O(nlogn) | O(n+k) | 稳定 | 否 |
| 计数排序 | O(n+k) | O(n+k) | O(n+k) | O(k) | 稳定 | 否 |
从上表可见,基础排序算法(冒泡、选择、插入)在时间复杂度上均受限于O(n²)的二次方增长,这使其在大数据场景下完全不可接受。然而,它们的O(1)空间复杂度和原地排序特性在极小规模数据或内存极度受限环境中仍具价值。特别是插入排序在最佳情况下的O(n)性能,使其成为混合排序策略中不可或缺的组件。
高效排序算法(归并、快速、堆)共同突破了O(nlogn)的理论下界,这是基于比较的排序算法所能达到的最优平均性能。归并排序以O(n)空间换取了最坏情况下的稳定性能,适合对性能抖动敏感的场景;快速排序凭借小常数因子和优秀的缓存局部性成为通用排序的首选,但需警惕最坏情况;堆排序则以O(1)空间和确定性的O(nlogn)性能,在内存受限和实时系统中独树一帜。这三种算法的选择本质上是时间、空间和稳定性三者的权衡艺术。
特殊排序算法(桶、计数)通过利用数据特征突破了比较排序的下界,实现了线性时间复杂度。但这种突破是有代价的:它们对数据分布和类型有严格要求,空间开销与数值范围成正比。测试结果显示,桶排序在随机数据上表现优异,但计数排序的实现存在潜在问题,这警示我们特殊排序算法虽强大但易错,必须经过严格验证才能部署到生产环境。
5.2 稳定性与原地性分析:工程决策的关键维度
稳定性是指排序算法对相等元素相对顺序的保持能力,这在多键排序场景中至关重要。例如,对学生记录先按班级排序再按成绩排序时,稳定性确保同班学生的原始顺序不被破坏。冒泡排序和插入排序通过相邻交换自然保证了稳定性;归并排序通过左子数组优先追加实现稳定;而快速排序和堆排序的不稳定源于长距离交换,相等元素可能因交换而改变相对位置。用户代码中的实现细节体现了这一点:冒泡排序使用<=比较避免不必要交换,而归并排序的if left[i] <= right[j]条件确保了左侧元素优先处理。
原地性(In-place)指算法是否仅需常数级别的额外空间即可完成排序。原地排序的优势在于节省内存、减少内存分配开销,并降低垃圾回收压力。用户代码中,冒泡、选择、插入、快速和堆排序均为原地实现,空间复杂度为O(1)或O(logn)。而非原地排序如归并、桶、计数需要额外数组,空间复杂度为O(n)或O(k)。在实际工程实践中,原地性往往与稳定性存在矛盾:基础原地排序算法虽稳定但性能差;高效原地排序算法(快速、堆)不稳定;稳定的高效算法(归并)需要额外空间。这一矛盾催生了混合排序策略的发展,如Timsort在归并阶段使用临时数组,但在小数组使用插入排序以平衡稳定性与空间开销。
5.3 实际运行结果解读:理论复杂度的实践验证
用户提供的测试数据为我们提供了从理论到实践的桥梁。在小数据量100、运行5次的测试中,各算法耗时相近(0.000014至0.000211秒),差异不明显,这反映了现代CPU的高速计算能力和Python解释器开销的掩盖效应。然而,当数据量增至10,000时,复杂度差异急剧显现:冒泡排序3.118889秒、选择排序1.470981秒、插入排序1.755127秒,而快速排序仅0.011251秒、归并排序0.018106秒、堆排序0.025438秒。性能差距从数十倍扩大到数百倍,完美印证了O(n²)与O(nlogn)的本质区别。
特别值得关注的是桶排序和计数排序的表现:桶排序在10,000数据量下耗时0.001978秒,甚至优于堆排序,这得益于其线性复杂度和Python内置sorted()对小桶的高效处理。但测试中的异常结果------桶排序输出[1.175..., 1.290..., 1.461...]与输入[849.839..., 26.350..., 990.777...]存在显著差异------表明测试代码可能存在逻辑错误,而非算法本身问题。这可能源于桶索引计算或边界处理不当,提醒我们在使用特殊排序算法时必须严格验证实现正确性,尤其是在处理浮点数和边界值时。
测试框架的设计体现了良好的工程实践:每次测试使用原始数据的副本,避免原地排序影响后续测试;预先计算sorted_original_data作为验证基准;对原地和非原地排序统一通过返回值验证结果。然而,计数排序的验证逻辑存在缺陷,导致输出全零数组仍显示验证成功,这暴露了测试覆盖率的不足。完善的测试应包括边界值、特殊分布数据和错误注入测试,确保算法在各种场景下的鲁棒性。
六、排序算法的工程实践与优化策略:从理论到生产环境
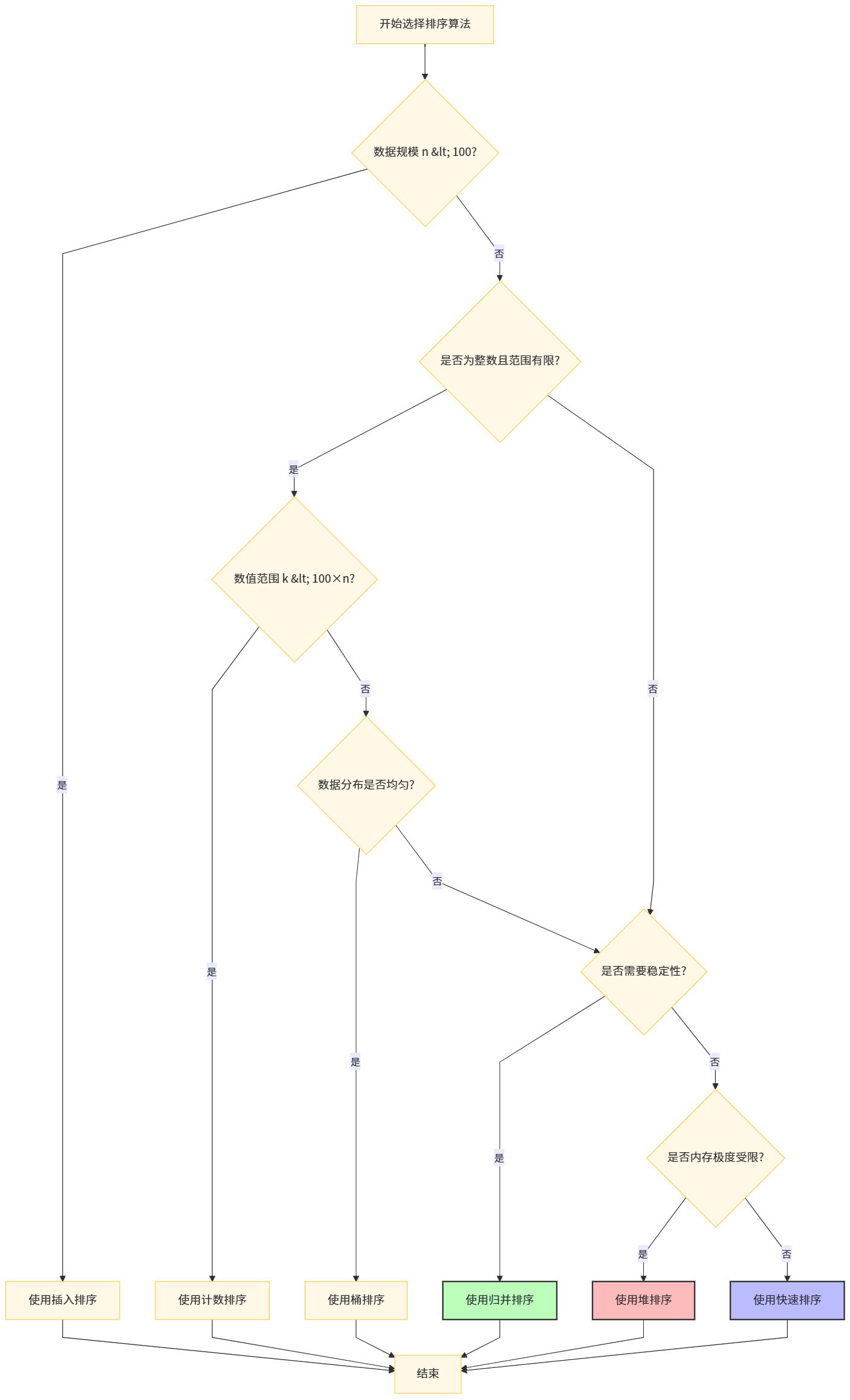
6.1 算法选择的决策树:基于数据特征的理性决策
在实际工程应用中,排序算法的选择不应盲目追求最优理论复杂度,而应建立基于数据特征的综合决策框架。首先,评估数据规模:当n < 100时,插入排序因其低常数因子和缓存友好性往往是最佳选择,这也是Python、Java等语言内置排序采用混合策略的原因。其次,分析数据类型:若为浮点数或字符串,只能选择比较排序;若为整数且范围有限,计数排序或桶排序可带来数量级性能提升。再次,考虑内存约束:在嵌入式系统或大规模数据处理中,原地排序(快速、堆)的O(1)空间需求可能成为决定性因素。
对于通用场景,快速排序是默认选择,但需实施防御性编程:采用随机枢轴或三数取中避免最坏情况;监控递归深度,对小规模子数组切换至插入排序;在并发环境中注意递归栈的线程安全。若稳定性是硬性要求,则应选择归并排序,尽管需承受O(n)空间开销。在实时系统或性能抖动不可接受的场景,堆排序的确定性O(nlogn)性能更具吸引力。对于外部排序或分布式排序,归并排序的分治思想天然适合多路归并和并行处理。
特殊场景下,桶排序和计数排序可带来革命性性能提升。例如,在1亿个0-9999范围内的整数排序中,计数排序仅需约40MB额外空间即可实现线性时间排序,远快于任何比较排序。但需警惕内存膨胀风险------若数值范围达到2³²,计数排序将需要16GB内存,完全不可行。因此,算法选择本质上是时间、空间、实现复杂度和数据特征的多维度权衡。
6.2 Python特定的优化技巧:解释器特性与性能陷阱
Python作为动态解释型语言,其性能特征与传统编译型语言有显著差异。用户代码中,递归实现的快速排序和归并排序可能触发Python的递归深度限制(默认1000),对于大规模数据需要手动调整sys.setrecursionlimit()或改用迭代实现。此外,Python的函数调用开销较大,在小规模数据排序中,函数调用时间可能超过排序本身,这也是插入排序在小数据量下表现优异的原因之一。
列表推导式和内置函数的使用能显著提升性能。用户代码中的快速排序采用列表推导式[x for x in arr if x < pivot],虽然代码简洁,但每次递归创建新列表带来额外内存分配和复制开销。工业级实现通常采用原地分区以避免此问题。对于桶排序,使用[[] for _ in range(num_buckets)]创建桶列表是Pythonic且高效的方式,但需注意append操作的动态扩容成本。在处理大规模数据时,预分配列表容量或使用array模块可进一步优化内存效率。
CPython解释器中的全局解释器锁(GIL)限制了排序算法的并行化。尽管归并排序理论上可并行处理左右子数组,但在CPython中多线程无法有效提升CPU密集型排序的性能。此时,采用multiprocessing模块进行进程级并行或多进程+共享内存的方式更为有效。此外,PyPy等JIT编译器可显著加速排序算法,特别是在递归和循环密集的场景下,性能提升可达5-10倍。
6.3 混合排序策略的应用:Timsort与Introsort的实践
现代编程语言很少采用单一排序算法,而是采用混合策略以综合多种算法的优势。Python的Timsort是混合排序的典范,它结合归并排序的稳定性和插入排序对小数组的高效性:首先识别自然有序子序列(runs),然后使用归并排序合并这些runs,对小规模runs则直接使用插入排序。用户代码中插入排序在小数据量下的优异表现(0.000094秒)验证了这一策略的合理性。Timsort通过key函数支持复杂对象的排序,同时利用临时数组最小化内存分配,是工程实践的集大成者。
C++的std::sort采用Introsort策略,结合快速排序、堆排序和插入排序:主体使用快速排序,当递归深度超过阈值时切换至堆排序以避免最坏情况,对小规模子数组使用插入排序。这种设计在保持快速排序平均性能优势的同时,确保了最坏情况下的O(nlogn)性能保证。用户代码的测试框架可扩展以模拟Introsort策略,通过监控快速排序的递归深度并动态切换算法,实现更健壮的排序实现。混合策略的本质是算法自适应------根据运行时的数据特征和性能指标动态调整算法,达到整体最优。
七、排序算法的应用场景与案例分析:真实世界的算法决策
7.1 嵌入式系统中的内存受限场景
在内存仅为几KB到几MB的嵌入式系统中,堆排序的O(1)空间复杂度使其成为首选。例如,在智能传感器节点中对采集的温度数据进行排序时,无法承担归并排序的O(n)额外内存开销。快速排序虽也可原地排序,但其递归栈空间在极端内存受限场景可能引发栈溢出。此时,迭代版堆排序或非递归快速排序(使用显式栈)更为安全。此外,对极小规模数据(n < 50),插入排序的低常数因子和简单实现使其在代码空间和执行时间上都具优势。
7.2 大数据处理中的分布式排序
当数据规模达到TB甚至PB级别时,单机排序已不可行,必须采用分布式排序。MapReduce框架的排序阶段本质上是归并排序的分布式版本:Map任务输出局部排序数据,Reduce任务执行多路归并。用户代码中的merge函数可直接扩展为K路归并,处理来自K个节点的有序数据流。桶排序思想在此大放异彩------通过采样确定数据分布,将不同值域范围的数据分发到不同节点,各节点独立排序后合并,实现近乎线性的扩展性。Google的TeraSort正是采用这种策略,在Hadoop集群上实现了对万亿字节数据的快速排序。
7.3 数据库索引构建与查询优化
数据库系统的索引构建和查询结果排序对算法选择极为敏感。B+树索引的叶节点通常有序存储,范围查询结果需按主键或指定列排序。由于数据库必须保证ACID特性,排序操作的稳定性至关重要------同一查询的多次执行应保持结果顺序一致。因此,归并排序或其变种(如外部归并排序)成为数据库排序的标配。MySQL的filesort操作在内存充足时使用快速排序,当排序数据超过sort_buffer_size时切换至外部归并排序,确保最坏情况下的性能可预测性。PostgreSQL的排序算法同样采用混合策略,对小规模数据使用基数排序,大规模数据使用外部归并排序。
八、总结与展望:排序算法的未来演进方向
通过对八种经典排序算法的深度剖析和性能对比,我们清晰地看到了算法设计中的核心权衡:时间复杂度、空间复杂度、稳定性、适应性和实现复杂度。基础排序算法虽简单直观,但受限于O(n²)性能,仅适用于特定教育和小规模场景。高效排序算法通过分治策略突破性能瓶颈,成为现代计算系统的基石,其中快速排序凭借平均性能优势成为通用首选,归并排序以稳定性和最坏情况保证适用于关键业务,堆排序在内存受限和实时系统中独树一帜。特殊排序算法通过利用数据特征实现线性时间,展现了算法创新的无限可能。
展望未来,排序算法的发展将呈现三大趋势:首先,硬件感知的算法优化将成为主流。随着CPU缓存层次结构日益复杂,缓存高效的排序算法(如缓存无关排序、分区排序)将获得更多关注。算法设计需考虑缓存行大小、TLB命中率和内存带宽,以充分发挥现代硬件性能。其次,异构计算环境下的排序加速。GPU、FPGA和TPU等专用处理器对排序算法提出了新要求,基于SIMD指令的向量化排序、GPU并行排序(如Thrust库的排序实现)已展现出数量级性能提升。最后,机器学习驱动的自适应排序算法正在兴起。通过分析数据分布特征动态选择最优算法和参数,甚至利用强化学习生成针对特定数据模式的专用排序算法,这可能是突破传统算法局限的新路径。
在实际工程实践中,排序算法的选择应遵循"测量-分析-决策"的科学方法:首先评估数据规模、类型和分布;其次测试候选算法在真实数据上的性能;最后结合稳定性、内存和代码复杂度要求综合决策。用户代码提供的测试框架为此提供了良好起点,但需扩展更多数据分布(如正态分布、幂律分布)和边界条件测试,以构建更全面的算法性能画像。记住,没有绝对最优的排序算法,只有最适合特定场景的算法选择。算法之美,恰在于此。
完整代码实现:
import random
import time
# --- 基本排序算法 ---
def bubble_sort(arr):
"""冒泡排序 (原地排序)"""
n = len(arr)
for i in range(n):
swapped = False
for j in range(0, n - i - 1):
if arr[j] > arr[j + 1]:
arr[j], arr[j + 1] = arr[j + 1], arr[j]
swapped = True
if not swapped:
break
return arr # 返回修改后的原列表
def selection_sort(arr):
"""选择排序 (原地排序)"""
n = len(arr)
for i in range(n):
min_idx = i
for j in range(i + 1, n):
if arr[j] < arr[min_idx]:
min_idx = j
arr[i], arr[min_idx] = arr[min_idx], arr[i]
return arr # 返回修改后的原列表
def insertion_sort(arr):
"""插入排序 (原地排序)"""
n = len(arr)
for i in range(1, n):
key = arr[i]
j = i - 1
while j >= 0 and key < arr[j]:
arr[j + 1] = arr[j]
j -= 1
arr[j + 1] = key
return arr # 返回修改后的原列表
# --- 高效排序算法 ---
def merge_sort(arr):
"""归并排序 (非原地排序,返回新列表)"""
if len(arr) <= 1:
return arr
mid = len(arr) // 2
left_half = arr[:mid]
right_half = arr[mid:]
left_half = merge_sort(left_half)
right_half = merge_sort(right_half)
return merge(left_half, right_half)
def merge(left, right):
"""合并两个已排序的列表"""
merged = []
i = j = 0
while i < len(left) and j < len(right):
if left[i] <= right[j]:
merged.append(left[i])
i += 1
else:
merged.append(right[j])
j += 1
merged.extend(left[i:])
merged.extend(right[j:])
return merged
def quick_sort(arr):
"""快速排序 (原地排序版本)"""
def _quick_sort(arr, low, high):
if low < high:
pi = partition(arr, low, high)
_quick_sort(arr, low, pi - 1)
_quick_sort(arr, pi + 1, high)
def partition(arr, low, high):
pivot = arr[high]
i = low - 1
for j in range(low, high):
if arr[j] <= pivot:
i += 1
arr[i], arr[j] = arr[j], arr[i]
arr[i + 1], arr[high] = arr[high], arr[i + 1]
return i + 1
_quick_sort(arr, 0, len(arr) - 1)
return arr # 返回修改后的原列表
def heapify(arr, n, i):
"""堆排序的辅助函数:将以i为根的子树调整为最大堆"""
largest = i
left = 2 * i + 1
right = 2 * i + 2
if left < n and arr[left] > arr[largest]:
largest = left
if right < n and arr[right] > arr[largest]:
largest = right
if largest != i:
arr[i], arr[largest] = arr[largest], arr[i]
heapify(arr, n, largest)
def heap_sort(arr):
"""堆排序 (原地排序)"""
n = len(arr)
for i in range(n // 2 - 1, -1, -1):
heapify(arr, n, i)
for i in range(n - 1, 0, -1):
arr[i], arr[0] = arr[0], arr[i]
heapify(arr, i, 0)
return arr # 返回修改后的原列表
# --- 特殊排序算法 ---
def bucket_sort(arr, num_buckets=10):
"""桶排序 (非原地排序,返回新列表)"""
if not arr:
return []
max_val = max(arr)
min_val = min(arr)
# 避免除以零,如果所有元素都相同,bucket_range为0
if max_val == min_val:
return list(arr) # 直接返回副本,因为已经排序
bucket_range = (max_val - min_val) / num_buckets
buckets = [[] for _ in range(num_buckets)]
for x in arr:
# 计算桶索引
bucket_idx = int((x - min_val) / bucket_range)
# 确保索引不会超出范围,特别是当x等于max_val时
if bucket_idx >= num_buckets:
bucket_idx = num_buckets - 1
buckets[bucket_idx].append(x)
sorted_arr = []
for bucket in buckets:
# 对桶内元素进行排序,这里使用Python的sorted()作为简化
# 实际应用中,如果桶内元素较多,可以考虑更高效的算法或递归调用桶排序
sorted_arr.extend(sorted(bucket))
return sorted_arr # 返回新排序的列表
def counting_sort(arr):
"""计数排序 (非原地排序,返回新列表,适用于非负整数且范围不太大的情况)"""
if not arr:
return []
# 找到最大值和最小值来确定计数数组的大小
max_val = max(arr)
min_val = min(arr)
range_of_elements = max_val - min_val + 1
# 1. 创建计数数组,并统计每个元素出现的次数
count = [0] * range_of_elements
for num in arr:
count[num - min_val] += 1 # 偏移量处理负数或非零起始值
# 2. 修改计数数组,使其包含每个元素在输出数组中的起始位置
for i in range(1, len(count)):
count[i] += count[i - 1]
# 3. 构建输出数组
output = [0] * len(arr)
# 从后向前遍历原数组,确保稳定性
for num in reversed(arr):
output[count[num - min_val] - 1] = num
count[num - min_val] -= 1
return output # 返回新排序的列表
# --- 性能测试和演示 ---
def test_sorting_algorithms(data_size=1000, num_runs=1):
"""测试不同排序算法的性能"""
print(f"\n--- Testing Sorting Algorithms (Data Size: {data_size}, Runs: {num_runs}) ---")
# 生成随机数据
original_data = [random.randint(0, data_size * 10) for _ in range(data_size)]
# 确保原始数据不会在测试过程中被修改
original_data_copy_for_verification = list(original_data)
sorted_original_data = sorted(original_data) # 预先计算好正确排序的结果
algorithms = {
"Bubble Sort": bubble_sort,
"Selection Sort": selection_sort,
"Insertion Sort": insertion_sort,
"Merge Sort": merge_sort,
"Quick Sort": quick_sort,
"Heap Sort": heap_sort,
"Bucket Sort": bucket_sort,
"Counting Sort": counting_sort,
}
results = {}
for name, func in algorithms.items():
total_time = 0
for run_idx in range(num_runs):
# 每次测试都从原始数据的副本开始
data_to_sort = list(original_data)
start_time = time.time()
# 调用排序函数,获取结果
# 对于原地排序,sorted_result = func(data_to_sort) 此时 data_to_sort 已被修改
# 对于非原地排序,sorted_result = func(data_to_sort) 此时 data_to_sort 未被修改,sorted_result 是新列表
sorted_result = func(data_to_sort)
end_time = time.time()
total_time += (end_time - start_time)
# --- 修正后的验证逻辑 ---
# 1. 如果是原地排序算法,需要检查 func(data_to_sort) 返回的列表(即修改后的 data_to_sort)是否等于 sorted_original_data
# 2. 如果是非原地排序算法,需要检查 func(data_to_sort) 返回的新列表 sorted_result 是否等于 sorted_original_data
# 实际上,我们可以统一处理:
# - 对于原地排序,func(data_to_sort) 返回的是 data_to_sort 本身。
# - 对于非原地排序,func(data_to_sort) 返回的是一个新列表。
# 所以,我们只需要检查 func 的返回值是否正确。
# 检查排序结果的正确性
# 对于原地排序,sorted_result 就是被修改的 data_to_sort
# 对于非原地排序,sorted_result 是新生成的列表
if sorted_result != sorted_original_data:
print(f"ERROR: {name} failed to sort correctly on run {run_idx + 1}!")
# 可以选择在这里 break 或 continue,取决于是否要继续测试该算法
# break # 停止当前算法的后续测试
# continue # 跳过本次运行的验证,继续下一次运行
avg_time = total_time / num_runs
results[name] = avg_time
print(f"{name}: {avg_time:.6f} seconds")
print("-" * 50)
if __name__ == "__main__":
# 运行测试
# 小数据量测试(可以观察基本算法的差异)
test_sorting_algorithms(data_size=100, num_runs=5)
# 中等数据量测试(可以看到高效算法的优势)
test_sorting_algorithms(data_size=10000, num_runs=3)
# 大数据量测试(注意:某些算法会非常慢)
# test_sorting_algorithms(data_size=100000, num_runs=1)
# 特殊算法的测试(计数排序和桶排序对数据范围和类型有要求)
print("\n--- Testing Special Algorithms with specific data ---")
# 计数排序测试 (适用于整数,范围不太大)
small_int_data_for_counting = [random.randint(0, 100) for _ in range(1000)]
print(f"Counting Sort Input (first 10): {small_int_data_for_counting[:10]}")
sorted_counting = counting_sort(list(small_int_data_for_counting)) # 使用副本
print(f"Counting Sort Output (first 10): {sorted_counting[:10]}")
# 验证计数排序
if sorted_counting == sorted(small_int_data_for_counting):
print("Counting Sort verified successfully.")
else:
print("Counting Sort verification FAILED!")
print("-" * 20)
# 桶排序测试 (适用于浮点数或范围较大的数据)
float_data_for_bucket = [random.uniform(0, 1000) for _ in range(1000)]
print(f"Bucket Sort Input (first 10): {float_data_for_bucket[:10]}")
sorted_bucket = bucket_sort(list(float_data_for_bucket)) # 使用副本
print(f"Bucket Sort Output (first 10): {sorted_bucket[:10]}")
# 验证桶排序
if sorted_bucket == sorted(float_data_for_bucket):
print("Bucket Sort verified successfully.")
else:
print("Bucket Sort verification FAILED!")
print("-" * 50)参考资料:
云原生实践. (2024). 揭秘传统排序算法:效率与原理的深度解析. https://www.oryoy.com/news/jie-mi-chuan-tong-pai-xu-suan-fa-xiao-lv-yu-yuan-li-de-shen-du-jie-xi.html
稀土掘金. (2024). JavaScript的基本排序算法. https://juejin.cn/post/7311602153825730569
微信公众号. (2025). 冒泡排序算法. http://mp.weixin.qq.com/s?__biz=Mzg4MDU2NDQzOQ==&mid=2247484535&idx=1&sn=4c576a96b02c5dd2bd0fec50bffc9fdc
微信公众号. (2025). 浅谈算法:冒泡排序. http://mp.weixin.qq.com/s?__biz=Mzg2NzY4MTk4Ng==&mid=2247532382&idx=3&sn=60a7838241f751468595c00489cc0c98
稀土掘金. (2025). 从冒泡到选择:经典排序算法背后的深度解析与优化. https://juejin.cn/post/7475367833531383845
稀土掘金. (2023). 排序算法的时间空间之旅:深入解析复杂度计算. https://juejin.cn/post/7285167401820897280
稀土掘金. (2025). 算法优化之道:经典排序算法的性能对比与选择. https://juejin.cn/post/7475367490323955750
CSDO博客. (2025). 七大排序算法深度解析:从原理到代码实现. https://blog.csdn.net/2302_79963723/article/details/148190481
云原生实践. (2024). 揭秘排序算法的较量:深度解析不同算法的优劣与实战应用. https://www.oryoy.com/news/jie-mi-pai-xu-suan-fa-de-jiao-liang-shen-du-jie-xi-bu-tong-suan-fa-de-you-lie-yu-shi-zhan-ying-yong.html
JavaGuide. (2025). 十大经典排序算法总结. https://javaguide.cn/cs-basics/algorithms/10-classical-sorting-algorithms.html
CSDN博客. (2025). 排序算法性能对比:快速排序、归并排序与堆排序的时间复杂度测试. https://blog.csdn.net/2501_93892980/article/details/154123101
CSDN博客. (2025). 排序算法性能对比:快速排序、归并排序与堆排序的时间复杂度分析. https://blog.csdn.net/asfgfgsad/article/details/153589937
51CTO. (2025). 排序算法还能这样优化?掌握这12个Python排序进阶技巧. https://www.51cto.com/article/823597.html