【leetcode】排序数组:快速排序、堆排序、归并排序
1、题目

2、题解
2.1 快速排序
随机快排的写法有很多种,但是针对极端case,比如中间有很多重复的数字的case,有些写法会超时。
下面这种写法,两边下标的值如果相等的话,i和j可以同时向内收缩,可以很好地处理这种极端case,值得学习和理解。
java
伪代码步骤
1、选第一个下标的值为partition
2、i = 第一个下标+1
3、j = 最后一个下标
4、while true 循环
4.1 i<=最后一个下标 && i下标的值<partition:i++
4.2 j>=第一个下标+1 && j下标的值>partition:j--
4.3 如果i>=j:跳出循环
4.4 交换下标i和下标j位置的值,同时i++, j--
5、交换第一个下标和j位置的值
6、继续快排
class Solution {
private static final Random random = new Random();
public int[] sortArray(int[] nums) {
quickSort(nums, 0, nums.length-1);
return nums;
}
private void quickSort(int[] nums, int start, int end) {
if (start >= end) {
return;
}
int randomIdx = random.nextInt(start, end+1);
swap(nums, start, randomIdx);
// 选第一个元素为partition
int partition = nums[start];
int i = start+1;
int j = end;
while (true) {
// 下标i的左侧一定小于partition
while (i<=end && nums[i]<partition) {
i++;
}
// 下标j的右侧一定大于partition
while (j>=start+1 && nums[j]>partition) {
j--;
}
if (i >= j) {
break;
}
// 此时下标j一定小于等于partiton,下标i一定大于等于partition。
// 两边同时向内收缩,可以加快运行时间,避免部分极端case超时(比如中间有大量重复的数字的case)
swap(nums, i, j);
i++;
j--;
}
swap(nums, start, j);
quickSort(nums, start, j-1);
quickSort(nums, j+1, end);
}
private void swap(int[] nums, int left, int right) {
int tmp = nums[right];
nums[right] = nums[left];
nums[left] = tmp;
}
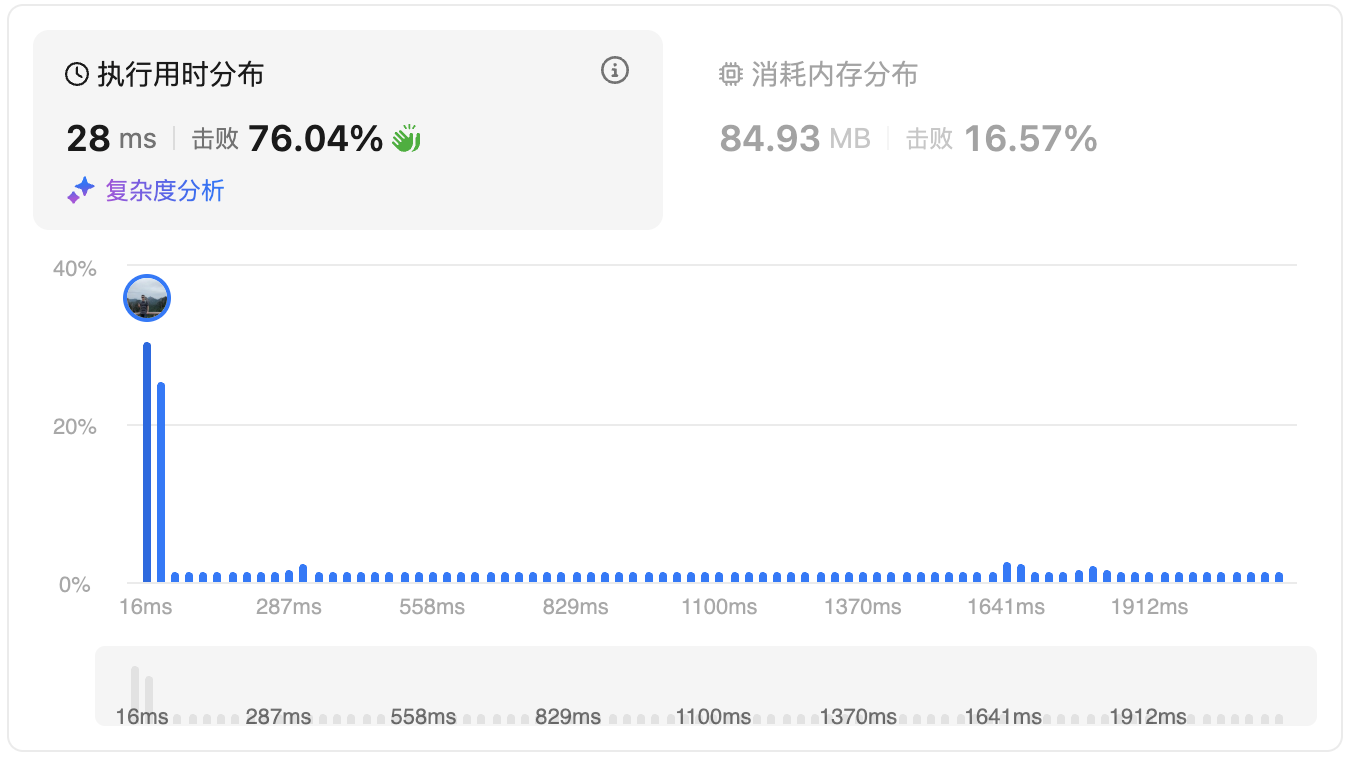
}提交结果:
2.2 堆排序
堆排序:
1、从后向前遍历元素,构建最大堆:当前位置(i)的左子节点(2i+1)或者右子节点(2 i+2)的值比当前位置的值大,则将当前位置与子节点位置的值交换,然后对子节点继续做heapify操作。即如果当前位置比左子节点和右子节点都大,则不需要调整。
2、从后先前遍历元素:先交换第一个位置(heapify操作后肯定是最大值)和最后一个位置的值,然后对第一个位置做heapify操作,操作完成后继续遍历。
java
class Solution {
public int[] sortArray(int[] nums) {
int len = nums.length;
// 1. 构建最大堆(从最后一个非叶子节点开始)
for (int i = len/2-1; i >= 0; --i) {
heapify(nums, len, i);
}
// 2. 逐个从堆顶取出元素,放到数组末尾
for (int i = len - 1; i > 0; i--) {
// 将当前堆顶元素(最大值)与数组末尾元素交换
swap(nums, 0, i);
// 调整剩余元素,使其保持最大堆性质
heapify(nums, i, 0);
}
return nums;
}
/**
* 调整堆,使其满足最大堆性质
* @param arr 待调整数组
* @param n 堆的大小(需要调整的元素个数)
* @param i 当前要调整的节点索引
*/
private static void heapify(int[] arr, int n, int i) {
int largest = i; // 初始化最大元素为当前节点
int left = 2 * i + 1; // 左子节点索引
int right = 2 * i + 2; // 右子节点索引
// 如果左子节点存在且大于当前最大节点
if (left < n && arr[left] > arr[largest]) {
largest = left;
}
// 如果右子节点存在且大于当前最大节点
if (right < n && arr[right] > arr[largest]) {
largest = right;
}
// 如果最大元素不是当前节点,需要交换并递归调整
if (largest != i) {
swap(arr, i, largest);
// 递归调整受影响的子树
heapify(arr, n, largest);
}
}
private static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
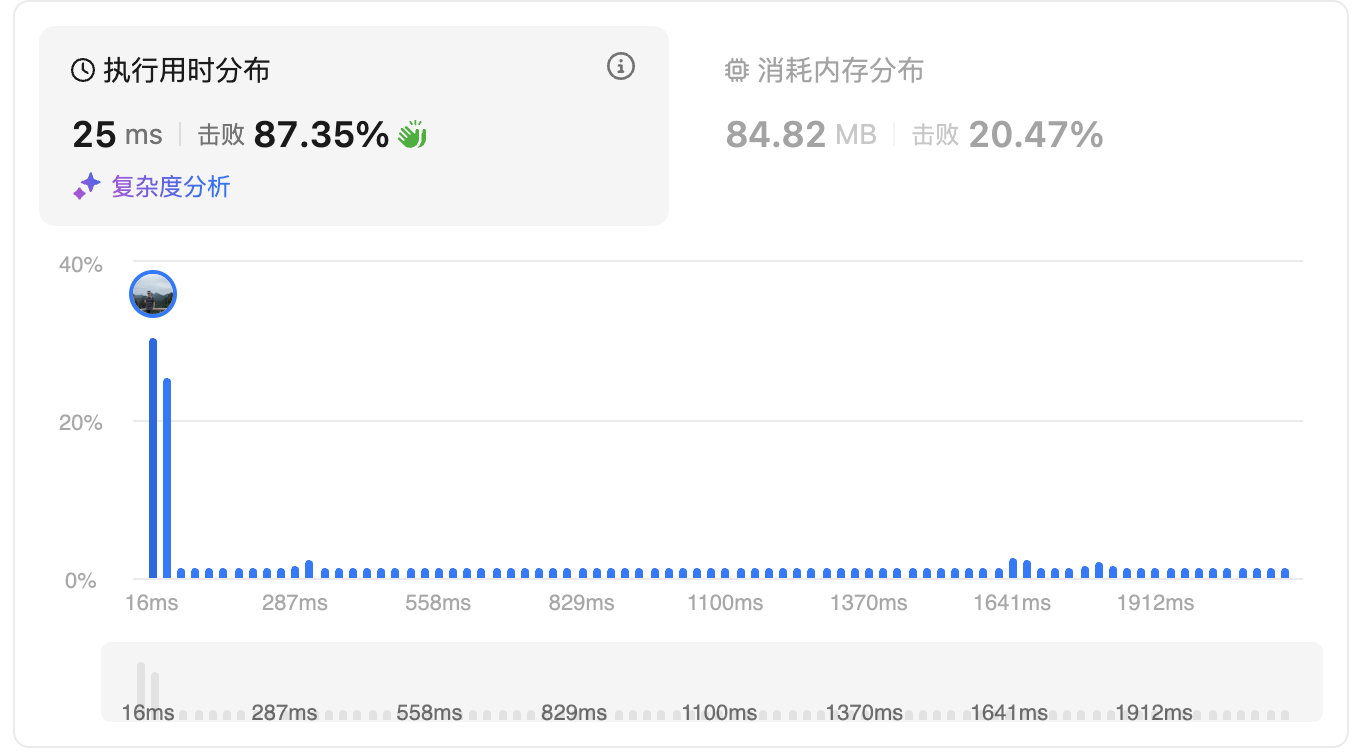
}提交结果:
2.3 归并排序
归并排序
1、开始下标大于等于末尾下标时,直接范围
1、找到开始下标和末尾下标的中点,将数组一分为2,继续递归进行排序
2、左半部分和右半部分有序后,新建一个相同长度的新数组,利用2个指针,依次将较小值赋值给新数组。最后将整理有序后的新数组再赋值回原数组。
java
class Solution {
public int[] sortArray(int[] nums) {
mergeSort(nums, 0, nums.length-1);
return nums;
}
private void mergeSort(int[] nums, int start, int end) {
if (start>=end) {
return;
}
int mid = (start+end) / 2;
mergeSort(nums, start, mid);
mergeSort(nums, mid+1, end);
int[] numsCopy = new int[end-start+1];
int idx = 0;
int left = start;
int right = mid+1;
while (left<=mid && right<=end) {
if (nums[left]<=nums[right]) {
numsCopy[idx++] = nums[left++];
} else {
numsCopy[idx++] = nums[right++];
}
}
while (left<=mid) {
numsCopy[idx++] = nums[left++];
}
while (right<=end) {
numsCopy[idx++] = nums[right++];
}
for (int i=start; i<=end; i++) {
nums[i] = numsCopy[i-start];
}
}
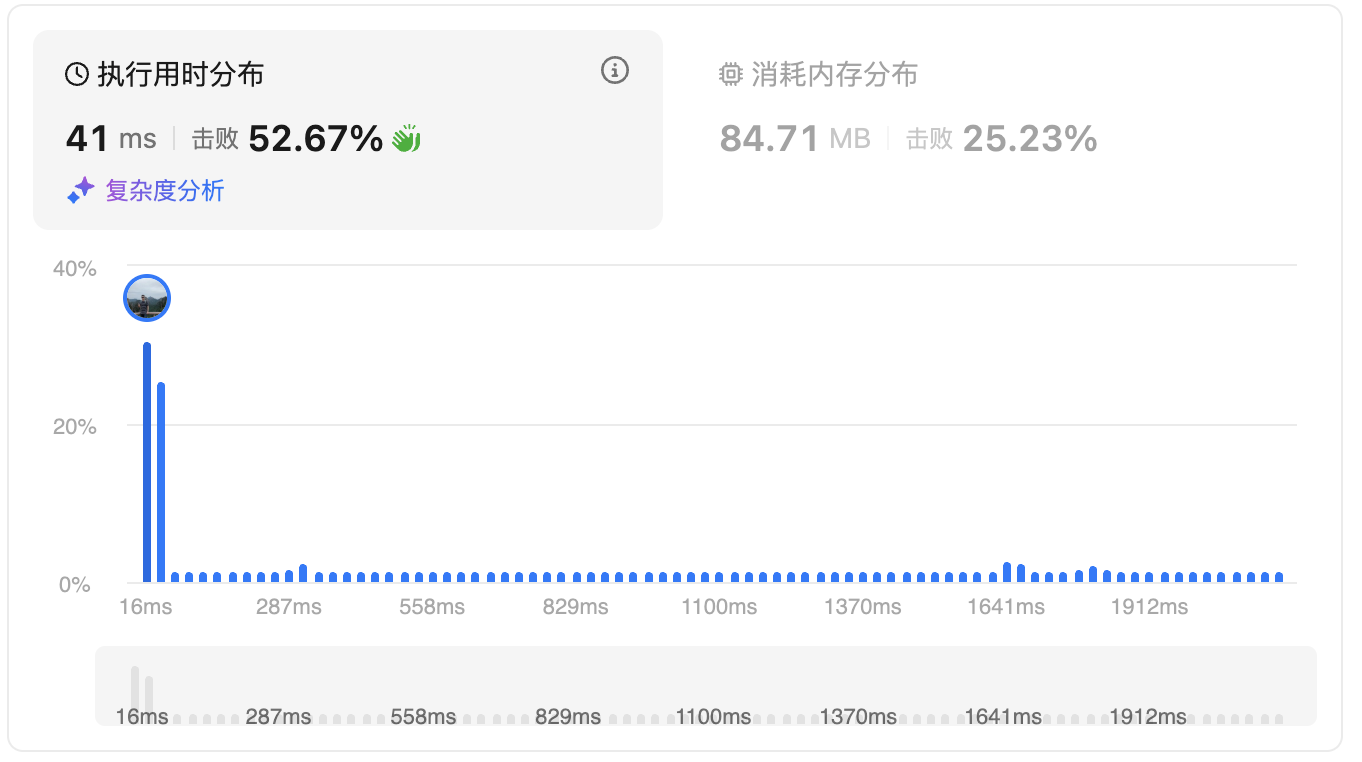
}提交结果: