深入解析MoE架构：大模型高效训练的核心技术

弓.长.2025-12-26 11:09

文章目录

深入解析MoE架构：大模型高效训练的核心技术

引言：大模型训练的效率困境

在人工智能快速发展的今天，大型语言模型的参数规模已从数亿增长到数万亿。2023年，GPT-4的参数数量据估计达到1.8万亿，而谷歌的PaLM模型更是达到了惊人的5400亿参数。这种规模的增长带来了前所未有的性能提升，但同时也带来了巨大的计算挑战。

传统的密集模型架构面临着一个基本矛盾：模型规模与计算效率之间的权衡。当我们将模型参数增加10倍时，训练所需的计算资源通常会增加数十倍，推理延迟也会显著增加。这种指数级的增长使得大模型的训练和部署成本变得极其昂贵。

正是为了解决这一核心矛盾，混合专家（Mixture of Experts，MoE）架构应运而生。本文将深入探讨MoE架构的技术原理、实现方式、应用场景以及未来发展方向，为您揭示这一支撑现代大模型高效训练的核心技术。

一、MoE架构的基本概念与历史演进

1.1 什么是混合专家（MoE）架构？

混合专家模型是一种稀疏激活 的神经网络架构，其核心思想是将一个大型网络分解为多个"专家"子网络，但每次前向传播只激活其中的一小部分专家。这种设计允许模型在参数量巨大的同时，保持相对较低的计算成本。

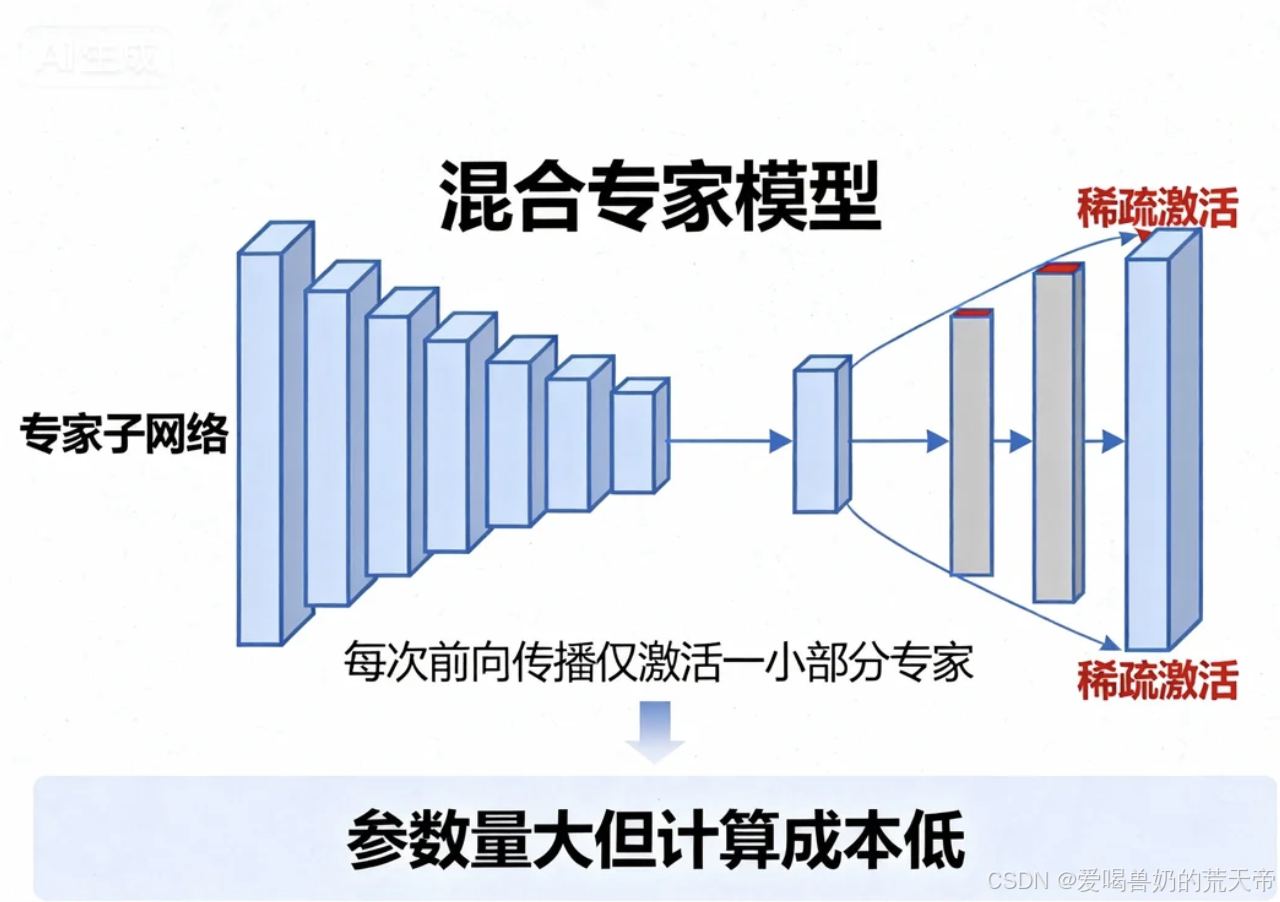
通俗理解：想象一个大型医院有100位各领域的专家医生，但每位病人只需要根据病情选择2-3位最相关的专家进行会诊。MoE就是这种"按需激活"的思想在神经网络中的体现。

1.2 MoE的历史发展脉络

MoE并非全新概念，其发展经历了几个关键阶段：

  • 1991年：MoE概念首次由Jacobs等人提出，最初用于解决分类任务
  • 2017年：Google Brain团队将MoE应用于大规模语言模型，推出Sparsely-Gated MoE
  • 2020年：GShard（Google）将MoE扩展到分布式训练，实现6000亿参数模型
  • 2021年：Switch Transformer（Google）简化MoE架构，实现万亿参数模型
  • 2022-2024年：MoE成为大模型标配，GPT-4、Mixtral-8x7B、DeepSeek等均采用此架构

二、MoE架构的深入技术解析

2.1 核心组件与工作流程

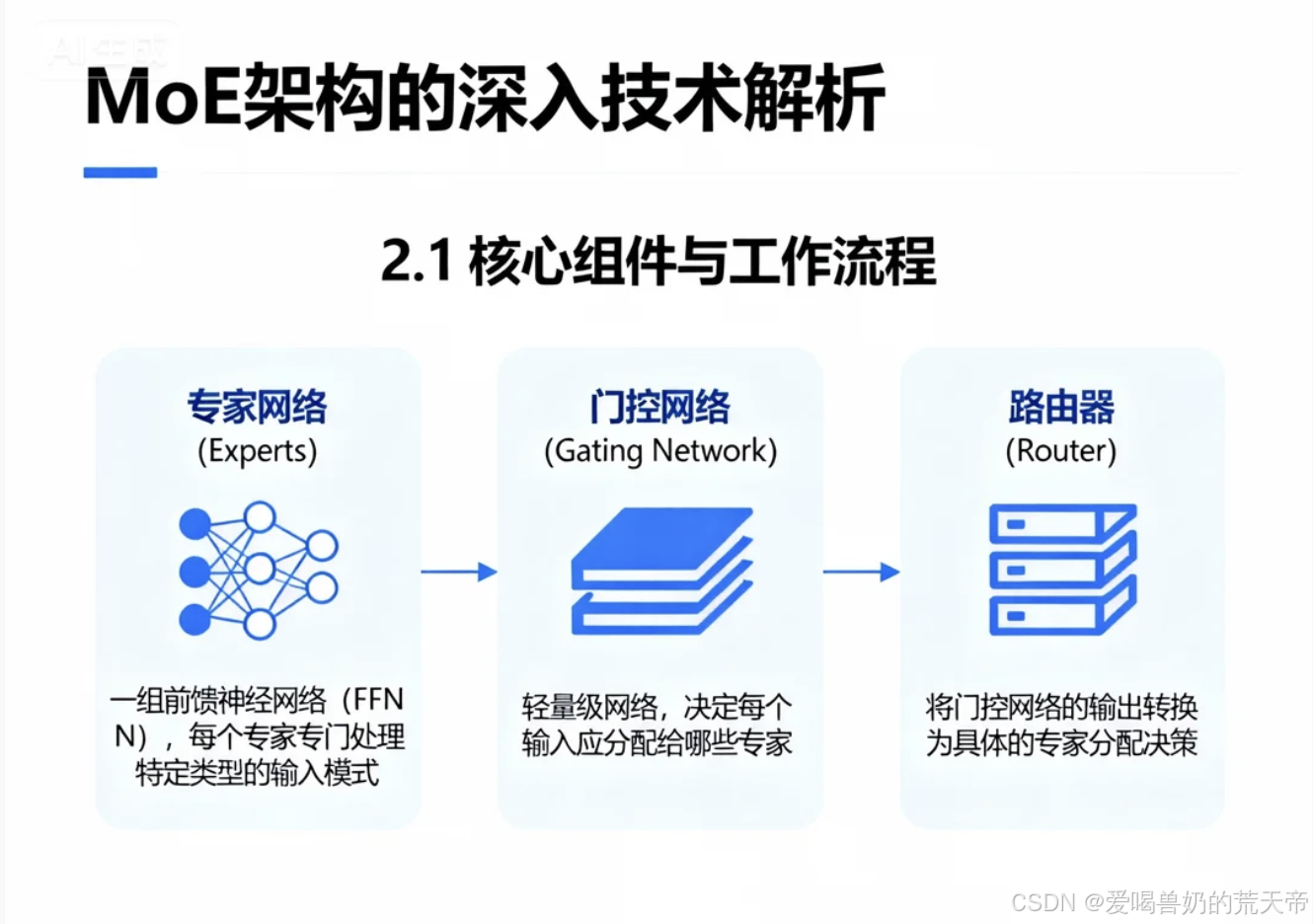
一个标准的MoE层包含三个核心组件：

  1. 专家网络（Experts）：一组前馈神经网络（FFN），每个专家专门处理特定类型的输入模式
  2. 门控网络（Gating Network）：轻量级网络，决定每个输入应分配给哪些专家
  3. 路由器（Router）：将门控网络的输出转换为具体的专家分配决策
python 复制代码 
import torch
import torch.nn as nn
import torch.nn.functional as F

class Expert(nn.Module):
    """单个专家网络，通常是一个前馈神经网络"""
    def __init__(self, input_dim, hidden_dim, output_dim):
        super().__init__()
        self.fc1 = nn.Linear(input_dim, hidden_dim)
        self.fc2 = nn.Linear(hidden_dim, output_dim)
        self.dropout = nn.Dropout(0.1)
        
    def forward(self, x):
        x = self.fc1(x)
        x = F.gelu(x)  # 使用GELU激活函数
        x = self.dropout(x)
        x = self.fc2(x)
        return x


class SparseMoELayer(nn.Module):
    """稀疏MoE层实现"""
    def __init__(self, input_dim, output_dim, num_experts=8, capacity_factor=1.0, top_k=2):
        super().__init__()
        self.input_dim = input_dim
        self.output_dim = output_dim
        self.num_experts = num_experts
        self.capacity_factor = capacity_factor
        self.top_k = top_k  # 每个输入激活的专家数量
        
        # 创建专家池
        self.experts = nn.ModuleList([
            Expert(input_dim, 4 * input_dim, output_dim) 
            for _ in range(num_experts)
        ])
        
        # 门控网络
        self.gate = nn.Linear(input_dim, num_experts)
        
    def forward(self, x):
        """
        前向传播过程
        x: [batch_size, seq_len, input_dim]
        返回: [batch_size, seq_len, output_dim]
        """
        batch_size, seq_len, _ = x.shape
        x_flat = x.reshape(-1, self.input_dim)  # 展平处理
        
        # 计算门控分数
        gate_logits = self.gate(x_flat)  # [batch_size*seq_len, num_experts]
        
        # 选择top_k专家
        top_k_vals, top_k_indices = torch.topk(
            gate_logits, 
            k=self.top_k, 
            dim=-1
        )
        
        # 计算门控权重（softmax over selected experts）
        top_k_weights = F.softmax(top_k_vals, dim=-1)
        
        # 初始化输出
        final_output = torch.zeros_like(x_flat)
        
        # 稀疏计算：只激活被选中的专家
        for expert_id in range(self.num_experts):
            # 找出需要当前专家处理的样本
            expert_mask = (top_k_indices == expert_id).any(dim=-1)
            
            if expert_mask.any():
                # 获取需要当前专家处理的输入
                expert_input = x_flat[expert_mask]
                
                # 计算专家输出
                expert_output = self.experts[expert_id](expert_input)
                
                # 获取对应的门控权重
                # 对于每个样本，找到当前专家在top_k中的位置
                sample_indices = torch.where(expert_mask)[0]
                weights_for_expert = torch.zeros(len(sample_indices), device=x.device)
                
                for i, sample_idx in enumerate(sample_indices):
                    # 找到该样本中当前专家的位置
                    expert_pos = (top_k_indices[sample_idx] == expert_id).nonzero(as_tuple=True)[0]
                    if len(expert_pos) > 0:
                        weights_for_expert[i] = top_k_weights[sample_idx, expert_pos[0]]
                
                # 加权求和
                final_output[expert_mask] += expert_output * weights_for_expert.unsqueeze(1)
        
        # 恢复原始形状
        return final_output.reshape(batch_size, seq_len, self.output_dim)

2.2 负载均衡机制：MoE的关键挑战与解决方案

负载不均衡是MoE架构面临的核心挑战之一。如果没有适当的控制机制，可能会出现"赢者通吃"现象------少数专家处理大部分输入，而多数专家很少被激活。

负载均衡的三种主要策略：

python 复制代码 
class LoadBalancingMoE(SparseMoELayer):
    """带有负载均衡的MoE层"""
    def __init__(self, input_dim, output_dim, num_experts=8, 
                 top_k=2, balance_loss_weight=0.01):
        super().__init__(input_dim, output_dim, num_experts, top_k)
        self.balance_loss_weight = balance_loss_weight
        
    def compute_load_balancing_loss(self, gate_logits, top_k_indices):
        """
        计算负载均衡损失
        gate_logits: [batch_size*seq_len, num_experts]
        top_k_indices: [batch_size*seq_len, top_k]
        """
        batch_size_seq_len = gate_logits.shape[0]
        
        # 计算每个专家的选择概率（使用softmax）
        probs = F.softmax(gate_logits, dim=-1)  # [batch_size*seq_len, num_experts]
        
        # 计算每个专家的被选次数
        expert_mask = torch.zeros(
            (batch_size_seq_len, self.num_experts),
            device=gate_logits.device
        )
        
        # 创建one-hot编码的专家选择矩阵
        for k in range(self.top_k):
            expert_mask.scatter_(
                1, 
                top_k_indices[:, k:k+1], 
                1
            )
        
        # 计算负载均衡损失
        # 公式: L_balance = sum_i(sum_j P_ij * E_ij) / (N * E * sum_i P_i * E_i)
        P = probs.mean(dim=0)  # 平均选择概率 [num_experts]
        E = expert_mask.float().mean(dim=0)  # 实际选择频率 [num_experts]
        
        load_balance_loss = (P * E).sum() * self.num_experts
        
        return load_balance_loss
    
    def forward(self, x, return_balance_loss=False):
        # 标准前向传播
        batch_size, seq_len, _ = x.shape
        x_flat = x.reshape(-1, self.input_dim)
        
        gate_logits = self.gate(x_flat)
        top_k_vals, top_k_indices = torch.topk(gate_logits, k=self.top_k, dim=-1)
        top_k_weights = F.softmax(top_k_vals, dim=-1)
        
        # 计算负载均衡损失
        balance_loss = self.compute_load_balancing_loss(gate_logits, top_k_indices)
        
        # 稀疏计算（简化版）
        final_output = torch.zeros_like(x_flat)
        
        # 为简化示例，这里使用循环处理每个专家
        for expert_id in range(self.num_experts):
            expert_mask = (top_k_indices == expert_id).any(dim=-1)
            if expert_mask.any():
                expert_input = x_flat[expert_mask]
                expert_output = self.experts[expert_id](expert_input)
                
                # 获取对应权重
                sample_indices = torch.where(expert_mask)[0]
                weights = torch.zeros(len(sample_indices), device=x.device)
                
                for i, idx in enumerate(sample_indices):
                    expert_pos = (top_k_indices[idx] == expert_id).nonzero(as_tuple=True)[0]
                    if len(expert_pos) > 0:
                        weights[i] = top_k_weights[idx, expert_pos[0]]
                
                final_output[expert_mask] += expert_output * weights.unsqueeze(1)
        
        output = final_output.reshape(batch_size, seq_len, self.output_dim)
        
        if return_balance_loss:
            return output, balance_loss * self.balance_loss_weight
        
        return output

2.3 容量因子与溢出处理

在实际部署中，MoE层需要处理专家容量限制的问题。每个专家只能处理有限数量的token，超出部分需要特殊处理。

python 复制代码 
class MoEWithCapacity(SparseMoELayer):
    """带有容量控制的MoE层"""
    def __init__(self, input_dim, output_dim, num_experts=8, 
                 top_k=2, capacity_factor=1.2):
        super().__init__(input_dim, output_dim, num_experts, top_k)
        self.capacity_factor = capacity_factor
        
    def forward(self, x):
        batch_size, seq_len, input_dim = x.shape
        num_tokens = batch_size * seq_len
        
        # 计算每个专家的容量
        expert_capacity = int(self.capacity_factor * num_tokens / self.num_experts)
        expert_capacity = max(expert_capacity, 4)  # 确保最小容量
        
        # 展平输入
        x_flat = x.reshape(-1, input_dim)
        
        # 门控计算
        gate_logits = self.gate(x_flat)
        top_k_vals, top_k_indices = torch.topk(gate_logits, k=self.top_k, dim=-1)
        top_k_weights = F.softmax(top_k_vals, dim=-1)
        
        # 创建调度矩阵
        final_output = torch.zeros_like(x_flat)
        
        # 处理每个专家
        for expert_id in range(self.num_experts):
            # 找到需要该专家的所有token
            token_indices = torch.where((top_k_indices == expert_id).any(dim=1))[0]
            
            if len(token_indices) == 0:
                continue
                
            # 如果超过容量，只处理前capacity个token
            if len(token_indices) > expert_capacity:
                # 根据门控分数排序，选择分数最高的capacity个token
                expert_gates = gate_logits[token_indices, expert_id]
                _, sorted_indices = torch.topk(expert_gates, k=expert_capacity)
                selected_tokens = token_indices[sorted_indices]
                
                # 标记溢出的token（可选：用其他专家处理或丢弃）
                overflow_tokens = token_indices[~torch.isin(token_indices, selected_tokens)]
                # 这里简单丢弃溢出token，实际应用中可能需要更复杂的处理
            else:
                selected_tokens = token_indices
            
            if len(selected_tokens) > 0:
                # 处理选中的token
                expert_input = x_flat[selected_tokens]
                expert_output = self.experts[expert_id](expert_input)
                
                # 应用权重
                for i, token_idx in enumerate(selected_tokens):
                    # 找到该token中当前专家的位置
                    pos = (top_k_indices[token_idx] == expert_id).nonzero(as_tuple=True)[0]
                    if len(pos) > 0:
                        weight = top_k_weights[token_idx, pos[0]]
                        final_output[token_idx] += expert_output[i] * weight
        
        return final_output.reshape(batch_size, seq_len, self.output_dim)

三、MoE在现代大模型中的应用实践

3.1 GPT-4的MoE实现特点

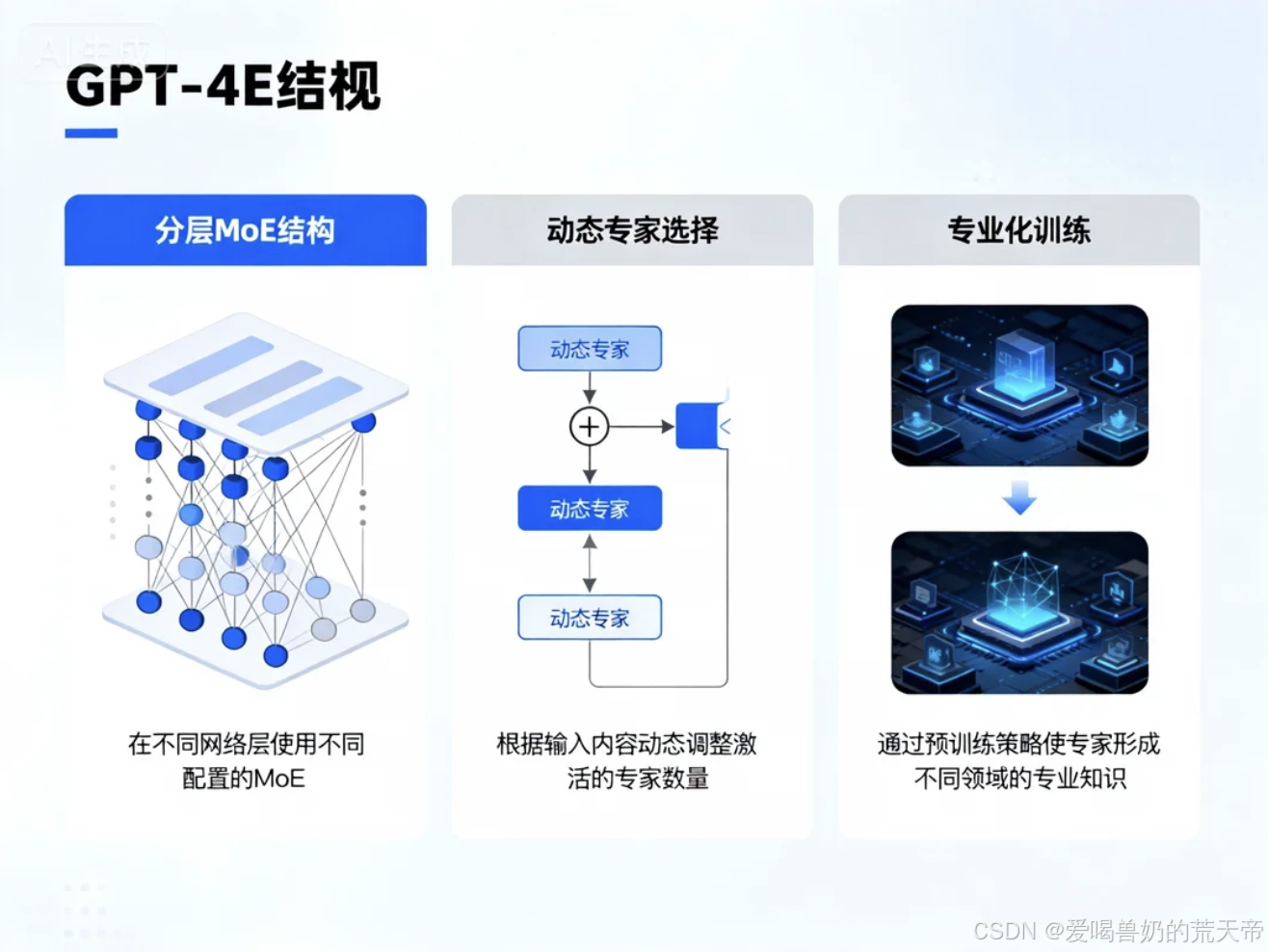
根据OpenAI公开的技术报告和相关信息，GPT-4的MoE实现具有以下特点：

  1. 分层MoE结构：在不同网络层使用不同配置的MoE
  2. 动态专家选择：根据输入内容动态调整激活的专家数量
  3. 专业化训练：通过预训练策略使专家形成不同领域的专业知识
python 复制代码 
class GPT4StyleMoE(nn.Module):
    """模拟GPT-4风格的MoE实现"""
    def __init__(self, config):
        super().__init__()
        self.config = config
        self.num_layers = config.num_layers
        
        # 创建不同配置的MoE层
        self.moe_layers = nn.ModuleList()
        for layer_idx in range(self.num_layers):
            # 在不同层使用不同数量的专家
            if layer_idx < config.num_layers // 3:
                num_experts = 4  # 底层使用较少专家
            elif layer_idx < 2 * config.num_layers // 3:
                num_experts = 8  # 中层
            else:
                num_experts = 16  # 高层使用更多专家
                
            moe_layer = LoadBalancingMoE(
                input_dim=config.hidden_size,
                output_dim=config.hidden_size,
                num_experts=num_experts,
                top_k=config.moe_top_k,
                balance_loss_weight=config.balance_loss_weight
            )
            self.moe_layers.append(moe_layer)
            
    def forward(self, hidden_states):
        """前向传播"""
        moe_losses = []
        
        for i, moe_layer in enumerate(self.moe_layers):
            # 残差连接
            residual = hidden_states
            
            # 通过MoE层
            if self.training:
                hidden_states, balance_loss = moe_layer(
                    hidden_states, 
                    return_balance_loss=True
                )
                moe_losses.append(balance_loss)
            else:
                hidden_states = moe_layer(hidden_states)
            
            # 层归一化和残差连接
            hidden_states = F.layer_norm(
                hidden_states + residual,
                normalized_shape=(self.config.hidden_size,)
            )
        
        # 计算总的MoE损失
        total_moe_loss = torch.stack(moe_losses).mean() if moe_losses else None
        
        return hidden_states, total_moe_loss

3.2 DeepSeek的MoE优化策略

DeepSeek在MoE实现上进行了多项创新优化：

  1. 专家共享策略：在不同层之间共享部分专家参数
  2. 细粒度路由：在序列级别而非token级别进行专家选择
  3. 训练稳定性优化：特殊的初始化方法和梯度裁剪策略
python 复制代码 
class DeepSeekMoE(nn.Module):
    """DeepSeek风格的MoE实现"""
    def __init__(self, config):
        super().__init__()
        self.config = config
        
        # 共享专家池：所有层共享同一组专家
        self.shared_experts = nn.ModuleList([
            Expert(
                config.hidden_size,
                config.expert_hidden_size,
                config.hidden_size
            ) for _ in range(config.num_shared_experts)
        ])
        
        # 每层特定的门控网络
        self.layer_gates = nn.ModuleList([
            nn.Linear(config.hidden_size, config.num_shared_experts)
            for _ in range(config.num_layers)
        ])
        
        # 局部专家（每层独有的专家）
        self.local_experts = nn.ModuleList([
            nn.ModuleList([
                Expert(
                    config.hidden_size,
                    config.expert_hidden_size,
                    config.hidden_size
                ) for _ in range(config.num_local_experts)
            ]) for _ in range(config.num_layers)
        ])
        
        self.local_gates = nn.ModuleList([
            nn.Linear(config.hidden_size, config.num_local_experts)
            for _ in range(config.num_layers)
        ])
    
    def forward(self, hidden_states, layer_idx):
        """
        前向传播
        layer_idx: 当前层索引
        """
        batch_size, seq_len, hidden_dim = hidden_states.shape
        
        # 展平处理
        x_flat = hidden_states.reshape(-1, hidden_dim)
        
        # 共享专家计算
        shared_gate_logits = self.layer_gates[layer_idx](x_flat)
        shared_probs = F.softmax(shared_gate_logits, dim=-1)
        
        # 局部专家计算
        local_gate_logits = self.local_gates[layer_idx](x_flat)
        local_probs = F.softmax(local_gate_logits, dim=-1)
        
        # 合并专家输出
        output = torch.zeros_like(x_flat)
        
        # 处理共享专家
        top_k_shared = min(2, self.config.num_shared_experts)
        shared_top_k_vals, shared_top_k_indices = torch.topk(
            shared_probs, k=top_k_shared, dim=-1
        )
        shared_top_k_weights = F.softmax(shared_top_k_vals, dim=-1)
        
        for i in range(top_k_shared):
            expert_id = shared_top_k_indices[:, i]
            expert_weight = shared_top_k_weights[:, i]
            
            # 为每个样本选择对应的专家
            for batch_idx in range(x_flat.shape[0]):
                current_expert_id = expert_id[batch_idx].item()
                current_weight = expert_weight[batch_idx]
                
                expert_output = self.shared_experts[current_expert_id](
                    x_flat[batch_idx:batch_idx+1]
                )
                output[batch_idx] += expert_output.squeeze(0) * current_weight
        
        # 处理局部专家（类似方式）
        top_k_local = min(1, self.config.num_local_experts)
        local_top_k_vals, local_top_k_indices = torch.topk(
            local_probs, k=top_k_local, dim=-1
        )
        local_top_k_weights = F.softmax(local_top_k_vals, dim=-1)
        
        for i in range(top_k_local):
            expert_id = local_top_k_indices[:, i]
            expert_weight = local_top_k_weights[:, i]
            
            for batch_idx in range(x_flat.shape[0]):
                current_expert_id = expert_id[batch_idx].item()
                current_weight = expert_weight[batch_idx]
                
                expert_output = self.local_experts[layer_idx][current_expert_id](
                    x_flat[batch_idx:batch_idx+1]
                )
                output[batch_idx] += expert_output.squeeze(0) * current_weight
        
        return output.reshape(batch_size, seq_len, hidden_dim)

四、MoE的训练策略与优化技巧

4.1 两阶段训练策略

MoE模型通常采用两阶段训练策略：

python 复制代码 
class MoETrainingScheduler:
    """MoE训练调度器"""
    def __init__(self, total_steps, warmup_steps=1000):
        self.total_steps = total_steps
        self.warmup_steps = warmup_steps
        self.current_step = 0
        
    def get_training_phase(self):
        """获取当前训练阶段"""
        if self.current_step < self.warmup_steps:
            return "warmup"  # 热身阶段
        elif self.current_step < self.total_steps * 0.3:
            return "stage1"  # 第一阶段：基础能力训练
        else:
            return "stage2"  # 第二阶段：专家专业化训练
    
    def get_training_config(self, phase):
        """根据阶段返回训练配置"""
        configs = {
            "warmup": {
                "learning_rate": 1e-5,
                "balance_loss_weight": 0.0,  # 热身阶段不应用负载均衡损失
                "dropout_rate": 0.0,
                "gradient_clip": 1.0
            },
            "stage1": {
                "learning_rate": 3e-4,
                "balance_loss_weight": 0.01,
                "dropout_rate": 0.1,
                "gradient_clip": 0.5
            },
            "stage2": {
                "learning_rate": 1e-4,
                "balance_loss_weight": 0.02,  # 增加负载均衡约束
                "dropout_rate": 0.2,
                "gradient_clip": 0.2
            }
        }
        return configs.get(phase, configs["stage2"])
    
    def step(self):
        self.current_step += 1

4.2 专家专业化引导

为了促使不同专家形成专业化能力，可以采用以下策略：

python 复制代码 
class ExpertSpecializationTrainer:
    """专家专业化训练器"""
    def __init__(self, num_experts, specialization_dim=128):
        self.num_experts = num_experts
        self.specialization_dim = specialization_dim
        
        # 为每个专家创建一个专业化向量
        self.expert_specializations = nn.Parameter(
            torch.randn(num_experts, specialization_dim)
        )
        
        # 专业化目标：鼓励专家处理特定类型的输入
        self.specialization_loss_weight = 0.1
    
    def compute_specialization_loss(self, expert_outputs, expert_ids, input_features):
        """
        计算专业化损失
        expert_outputs: 专家输出列表
        expert_ids: 使用的专家ID
        input_features: 输入特征
        """
        loss = 0.0
        
        for expert_id in range(self.num_experts):
            # 找出该专家处理的样本
            mask = (expert_ids == expert_id)
            if mask.any():
                # 获取该专家处理的输入特征
                expert_inputs = input_features[mask]
                
                # 计算输入特征与专家专业化向量的相似度
                # 我们希望专家处理与其专业化方向相似的输入
                similarity = F.cosine_similarity(
                    expert_inputs[:, :self.specialization_dim],
                    self.expert_specializations[expert_id].unsqueeze(0),
                    dim=-1
                )
                
                # 专业化损失：鼓励相似度高
                loss += (1 - similarity.mean())
        
        return loss * self.specialization_loss_weight / self.num_experts

五、MoE的部署优化与推理加速

5.1 动态批处理与专家调度

在实际部署中，MoE模型的推理优化至关重要：

python 复制代码 
class MoEInferenceOptimizer:
    """MoE推理优化器"""
    def __init__(self, model, max_batch_size=32, use_cuda_graph=False):
        self.model = model
        self.max_batch_size = max_batch_size
        self.use_cuda_graph = use_cuda_graph
        
        # 缓存专家输出（针对重复计算）
        self.expert_cache = {}
        
    def optimize_inference(self, inputs):
        """
        优化推理过程
        inputs: 输入张量列表
        """
        # 动态批处理
        batched_inputs = self.dynamic_batching(inputs)
        
        # 专家调度优化
        optimized_outputs = []
        
        for batch in batched_inputs:
            # 预计算门控决策
            gate_decisions = self.precompute_gates(batch)
            
            # 优化专家调度
            expert_schedule = self.schedule_experts(gate_decisions)
            
            # 执行推理
            if self.use_cuda_graph and len(batch) == self.max_batch_size:
                output = self.cuda_graph_inference(batch, expert_schedule)
            else:
                output = self.standard_inference(batch, expert_schedule)
            
            optimized_outputs.append(output)
        
        return self.unbatch_outputs(optimized_outputs)
    
    def schedule_experts(self, gate_decisions):
        """优化专家调度，减少计算重叠"""
        # 按专家ID分组输入
        expert_groups = {}
        
        for token_idx, (expert_ids, weights) in enumerate(gate_decisions):
            for expert_id, weight in zip(expert_ids, weights):
                if expert_id not in expert_groups:
                    expert_groups[expert_id] = []
                expert_groups[expert_id].append((token_idx, weight))
        
        # 排序专家以减少内存跳转
        schedule = []
        for expert_id in sorted(expert_groups.keys()):
            schedule.append((expert_id, expert_groups[expert_id]))
        
        return schedule

5.2 量化与压缩策略

python 复制代码 
class MoEQuantizer:
    """MoE模型量化器"""
    def __init__(self, model, quantization_bits=8):
        self.model = model
        self.quantization_bits = quantization_bits
        
    def quantize_experts(self):
        """量化专家权重"""
        for name, module in self.model.named_modules():
            if isinstance(module, Expert):
                self.quantize_module(module)
    
    def quantize_module(self, module):
        """量化单个模块"""
        # 权重量化
        if hasattr(module, 'weight'):
            weight = module.weight.data
            quantized_weight = self.quantize_tensor(weight)
            module.weight.data = quantized_weight
        
        # 激活量化（动态范围）
        module.activation_precision = self.quantization_bits
    
    def quantize_tensor(self, tensor):
        """量化张量"""
        if self.quantization_bits == 8:
            # 8-bit量化
            scale = tensor.abs().max() / 127.0
            quantized = torch.clamp(torch.round(tensor / scale), -128, 127)
            return quantized * scale
        elif self.quantization_bits == 4:
            # 4-bit量化（更激进）
            # 这里使用简单的分块量化
            tensor_flat = tensor.flatten()
            num_blocks = (tensor_flat.shape[0] + 31) // 32
            
            quantized_blocks = []
            for i in range(num_blocks):
                block = tensor_flat[i*32:(i+1)*32]
                block_min, block_max = block.min(), block.max()
                scale = (block_max - block_min) / 15.0
                
                quantized_block = torch.clamp(
                    torch.round((block - block_min) / scale),
                    0, 15
                )
                quantized_blocks.append(quantized_block * scale + block_min)
            
            quantized = torch.cat(quantized_blocks)[:tensor_flat.shape[0]]
            return quantized.reshape(tensor.shape)
        
        return tensor

六、MoE的未来发展方向与挑战

6.1 技术挑战与解决方案

挑战 描述 当前解决方案 未来方向
负载不均衡 少数专家处理大部分输入 负载均衡损失函数 动态专家容量
通信开销 分布式训练中的专家通信 专家分组、分层MoE 更智能的路由策略
训练不稳定 MoE特有的梯度问题 梯度裁剪、特殊初始化 改进的优化算法
内存占用 专家参数存储 专家共享、参数复用 更高效的内存管理

6.2 未来研究方向

  1. 自适应MoE：根据输入复杂度动态调整专家数量
  2. 跨模态MoE：处理文本、图像、音频的多模态专家
  3. 联邦学习中的MoE：隐私保护下的分布式专家训练
  4. 神经架构搜索优化：自动发现最优MoE结构

七、实践指南：构建自己的MoE模型

7.1 快速开始示例

python 复制代码 
import torch
from torch import nn
import torch.nn.functional as F

class SimpleMoEModel(nn.Module):
    """简单的MoE模型示例"""
    def __init__(self, vocab_size=50000, hidden_size=768, 
                 num_experts=8, num_layers=12):
        super().__init__()
        
        # 词嵌入层
        self.embedding = nn.Embedding(vocab_size, hidden_size)
        
        # MoE层
        self.moe_layers = nn.ModuleList([
            SparseMoELayer(
                input_dim=hidden_size,
                output_dim=hidden_size,
                num_experts=num_experts,
                top_k=2
            ) for _ in range(num_layers)
        ])
        
        # 输出层
        self.output_layer = nn.Linear(hidden_size, vocab_size)
        
        # 层归一化
        self.layer_norm = nn.LayerNorm(hidden_size)
    
    def forward(self, input_ids):
        # 嵌入层
        x = self.embedding(input_ids)
        
        # 通过MoE层
        for moe_layer in self.moe_layers:
            residual = x
            x = moe_layer(x)
            x = self.layer_norm(x + residual)
        
        # 输出层
        logits = self.output_layer(x)
        
        return logits

# 使用示例
model = SimpleMoEModel()
input_ids = torch.randint(0, 50000, (4, 128))  # batch_size=4, seq_len=128
logits = model(input_ids)
print(f"输出形状: {logits.shape}")  # 应该是 [4, 128, 50000]

7.2 性能调优建议

  1. 专家数量选择：从小规模开始（4-8个专家），逐步增加
  2. 容量因子设置：开始时设为1.2-1.5，根据溢出率调整
  3. 负载均衡权重：从0.01开始，观察专家利用率
  4. 批处理策略：使用动态批处理优化推理速度

结论

MoE架构作为大模型高效训练的核心技术，已经在GPT-4、DeepSeek等先进模型中证明了其价值。通过稀疏激活机制，MoE在保持模型容量的同时大幅降低了计算成本，为实现更大规模的模型提供了可行的技术路径。

然而，MoE技术仍处于快速发展阶段，面临负载均衡、训练稳定性、推理优化等诸多挑战。随着研究的深入和工程实践的积累，我们有理由相信MoE将在未来的人工智能发展中发挥更加重要的作用。

对于开发者和研究者来说，理解MoE的原理和实现细节，掌握其优化技巧，将有助于构建更高效、更强大的AI系统。本文提供的代码示例和实践建议，希望能为您在MoE领域的探索提供有价值的参考。

相关推荐
微爱帮监所写信寄信2 小时前
微爱帮监狱寄信写信小程序工单系统技术方案：智能投诉处理与问题解决平台
人工智能·网络协议·安全·小程序·内容审核·监狱寄信
胡伯来了2 小时前
22 Transformers - 训练计算机视觉模型
人工智能·计算机视觉·transformer·transformers
Lun3866buzha2 小时前
心血管造影图像目标检测_YOLO11-CSFCN模型实现与优化_1
人工智能·目标检测·目标跟踪
谈思汽车2 小时前
车企如何拿到 ISO/PAS 8800 汽车AI安全流程认证！
人工智能·安全·ai·汽车·智能汽车
AndrewHZ2 小时前
【图像处理基石】什么是神经渲染？
图像处理·人工智能·神经网络·算法·cnn·计算机图形学·神经渲染
yy_xzz2 小时前
003 卷积神经网络（CNN）-- 原理到实践
人工智能·神经网络·cnn
雪花desu2 小时前
深入 LangChain LCEL 的 10 个核心特性
数据库·人工智能·深度学习·langchain
byzh_rc2 小时前
[模式识别-从入门到入土] 组合分类器
人工智能·算法·机器学习·支持向量机·概率论
zhongerzixunshi2 小时前
以技术创新为翼 筑就发展新高度
大数据·人工智能·物联网
热门推荐
01GitHub 镜像站点02从快手“12·22”直播攻击事件看：一次教科书式的业务层饱和攻击033D 圣诞树网页代码04UV安装并设置国内源05Linux下V2Ray安装配置指南06Gemini3 生成的基于手势控制3D粒子圣诞树07在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）08解决 WSL Ubuntu 中 /etc/resolv.conf 自动重置问题09开源分享 | 超浪漫 3D 圣诞树立体动画（附零基础使用教程）10GLM-4.7 vs MiniMax-M2.1：代码工程理解