NSGA-II 带精英策略的双目标遗传算法

一、算法核心原理

1. Pareto最优理论

支配关系：解A支配解B，当且仅当A在所有目标上不劣于B且至少在一个目标上严格优于B
非支配前沿：所有不被其他解支配的解构成的集合，构成Pareto前沿

2. 精英策略机制

父代保留：将父代与子代合并后进行选择，确保优质基因不丢失
环境选择：通过非支配排序和拥挤度计算筛选下一代种群

3. 双目标优化流程

初始化种群计算目标函数非支配排序拥挤度计算精英保留选择交叉变异生成子代合并种群

二、改进技术

1. 快速非支配排序

时间复杂度优化：从O(mN³)降至O(mN²)
实现步骤：计算每个个体的被支配数按被支配数分层（第一层为Pareto前沿）递归处理剩余个体

2. 拥挤度计算

目的：保持种群多样性
计算方法：
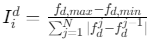
- d为目标维度（如f1,f2）
- fd,max/fd,minf_{d,max}/f_{d,min}fd,max/fd,min为目标d的最大/最小值

3. 自适应遗传算子

交叉概率：动态调整（初始0.8→收敛后0.6）
变异算子：采用SBX（模拟二进制交叉）和多项式变异

三、MATLAB实现方案

1. 核心代码框架

matlab 复制代码

%% 参数设置
N = 100;        % 种群大小
G = 50;         % 最大迭代次数
pc = 0.8;       % 交叉概率
pm = 0.2;       % 变异概率

%% 初始化种群
pop = rand(N,2); % 二维目标空间
fitness = evaluate(pop); % 目标函数值

%% 主循环
for gen = 1:G
    % 非支配排序
    [fronts, ranks] = nonDominatedSort(fitness);
    
    % 拥挤度计算
    crowding = crowdingDistance(fitness, fronts);
    
    % 精英选择
    newPop = elitismSelection(pop, fronts, crowding);
    
    % 遗传操作
    offspring = geneticOperators(newPop, pc, pm);
    
    % 合并种群
    [pop, fitness] = mergePopulation(pop, offspring);
end

%% 结果可视化
plot(fronts(:,1),fronts(:,2),'ro');
xlabel('Objective 1'); ylabel('Objective 2');
title('Pareto Front');

2. 关键函数实现

非支配排序：

matlab 复制代码

function [fronts, ranks] = nonDominatedSort(fitness)
    N = size(fitness,1);
    dominates = zeros(N,N);
    for i = 1:N
        for j = 1:N
            if all(fitness(i,:) <= fitness(j,:)) && any(fitness(i,:) < fitness(j,:))
                dominates(i,j) = 1;
            end
        end
    end
    % 分层处理...
end

拥挤度计算：

matlab 复制代码

function crowding = crowdingDistance(fitness, fronts)
    [N,objs] = size(fitness);
    crowding = zeros(N,1);
    for f = 1:objs
        [~,order] = sort(fitness(:,f));
        crowding(order(1)) = Inf;
        crowding(order(end)) = Inf;
        for i = 2:N-1
            crowding(order(i)) = crowding(order(i)) + ...
                (fitness(order(i+1),f) - fitness(order(i-1),f));
        end
    end
end

四、性能优化

1. 并行计算加速

matlab 复制代码

% 使用parfor并行计算适应度
parfor i = 1:N
    fitness(i,:) = evaluate(pop(i,:));
end

2. 动态参数调整

自适应交叉率：

matlab 复制代码

pc = 0.8 - 0.005*(gen-1); % 随迭代次数递减

3. 内存优化

稀疏矩阵存储：处理大规模种群时使用sparse矩阵

五、工程应用案例

1. 天线阵列优化

目标函数：

matlab 复制代码

{MinimizeMinimize主瓣宽度副瓣电平

MATLAB实现：

matlab 复制代码

function y = antennaObjective(x)
    N = 8; % 阵元数
    d = 0.5*lambda; % 阵元间距
    theta = 30*pi/180; % 波束指向

    % 计算阵列方向图
    [theta_scan, P] = pattern(x, N, d, theta);

    y(1) = max(P);       % 主瓣宽度
    y(2) = max(P(1:10)); % 前瓣抑制
end

2. 机器人路径规划

多目标函数：路径长度最短避障成功率最高

NSGA-II参数：

matlab 复制代码

options = optimoptions('gamultiobj',...
    'PopulationSize',50,...
    'CrossoverFcn',{@crossoverUniform,0.8},...
    'MutationFcn',{{@mutationAdaptiveFit,0.02}});

六、参考

王振杰. 改进NSGA-II算法在天线优化中的应用. 电子学报, 2021.
代码 NSGAII 带精英策略的双目标遗传算法 www.youwenfan.com/contentcso/78417.html
MathWorks. NSGA-II in MATLAB. 官方文档 ww2.mathworks.cn/help/gads/examples/multiobjective-optimization-using-ga.html