基本信息
来自中山大学,2025.10.27提交在arxiv上的论文,模型的名字和某个暗物质探测器相同(

论文地址:[2510.23273] A Novel Framework for Multi-Modal Protein Representation Learning
代码地址:https://anonymous.4open.science/r/DAMPE-ACD8
数据类型:用序列+结构+PPI,预测GO标签
数据集:与DPFunc论文使用的同一个数据集,从CAFA中筛选的59000+个蛋白质
模型结构
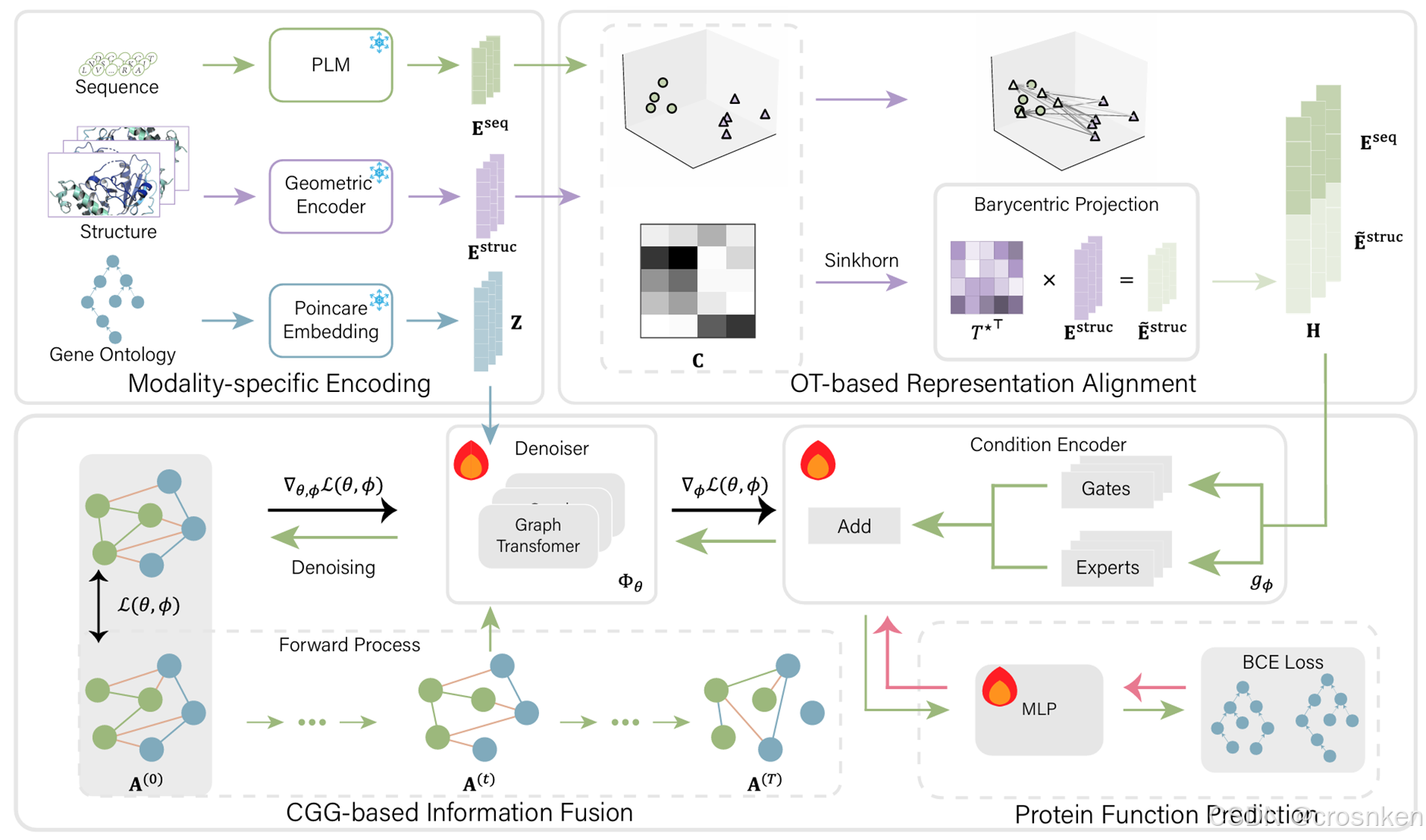
模型大体结构非常清晰,初始嵌入、特征对齐、异构图去噪、分类。
模型有很多比较新颖的点(个人观点)
1、Poincare嵌入(庞加莱嵌入,双曲几何嵌入)
这个东西一般是用于知识图谱的数据表征,这里它用来做GO的初始嵌入,也非常合适
 (图片来自网络)
(图片来自网络)
具体的数学原理比较复杂,我们只需要知道,越general的标签越靠近球的中心,越具体的标签越靠近球的边缘就可以了。除此之外,同层级的标签也会相互排斥,保证同级概念的差异性。
具体数学推导可以见这篇博客[论文笔记]Poincaré Embeddings & Hierarchical Represent - 知乎
没想到2019年就已经提出了,这篇文章的作者认为这个用途并不大,但其实用在这种具有层次结构的标签分类任务中还是挺合适的(
2、最优传输理论
最优传输问题是求解两个分布之间的最小距离
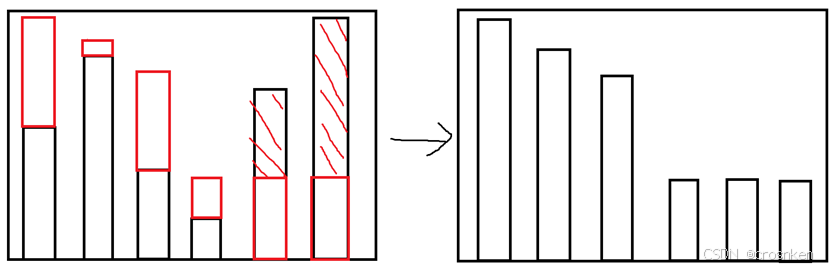
比如贪心的经典例题:均分纸牌,就是将一个离散的任意分布,以最小的代价转移为一个均匀离散分布。
再复杂一点,我们的目标分布可以不是均匀的,例如下图。它依旧有贪心算法能解决,推土机算法。不过它要求移动距离(单位代价)必须是两坐标的绝对值距离。
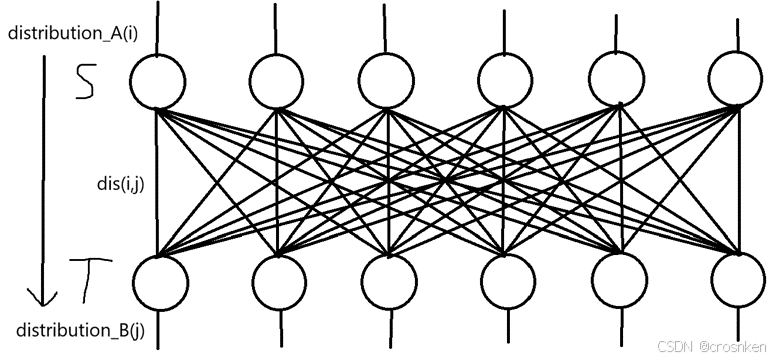
再复杂一点,我们重新定义距离,任意两点的距离表示为dis(i,j),我们可以构建以下的最小费用流模型来解决:
更加复杂的,还有连续分布的情况,不过也有通用的计算公式
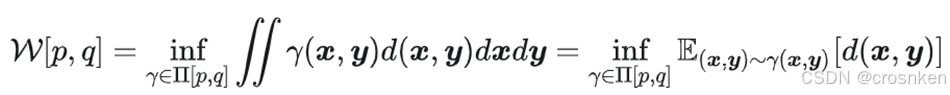
也可以采用的迭代算法来求解离散最优传输问题,Sinkhorn迭代

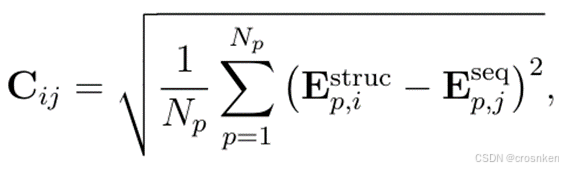
(这部分的数学理论非常多,我也没有研究太深,也有可能有些地方讲错了,还请大佬们指出)
在论文中,最优传输理论的运用就是,将结构的嵌入向量对齐到序列的嵌入向量上
利用Sinkhorn求解出的最优传输方案矩阵T*(过去是训练一个MLP映射)
用最小的代价,保持映射后的结构嵌入向量上各个位置的值与序列嵌入向量中的分布一致
3、异构图去噪
在蛋白质功能预测领域,利用异构图的论文已经非常多了,其实算不上新颖。
一旦要使用异构图,就必须考虑数据泄露的问题,测试集里面的蛋白质与GO信息很容易在训练中通过PPI网络和GO标注网络泄露出来。
不过这个模型的数据泄露的风险不高。异构图构建时清理了测试集蛋白质的Protein-GO标注边。
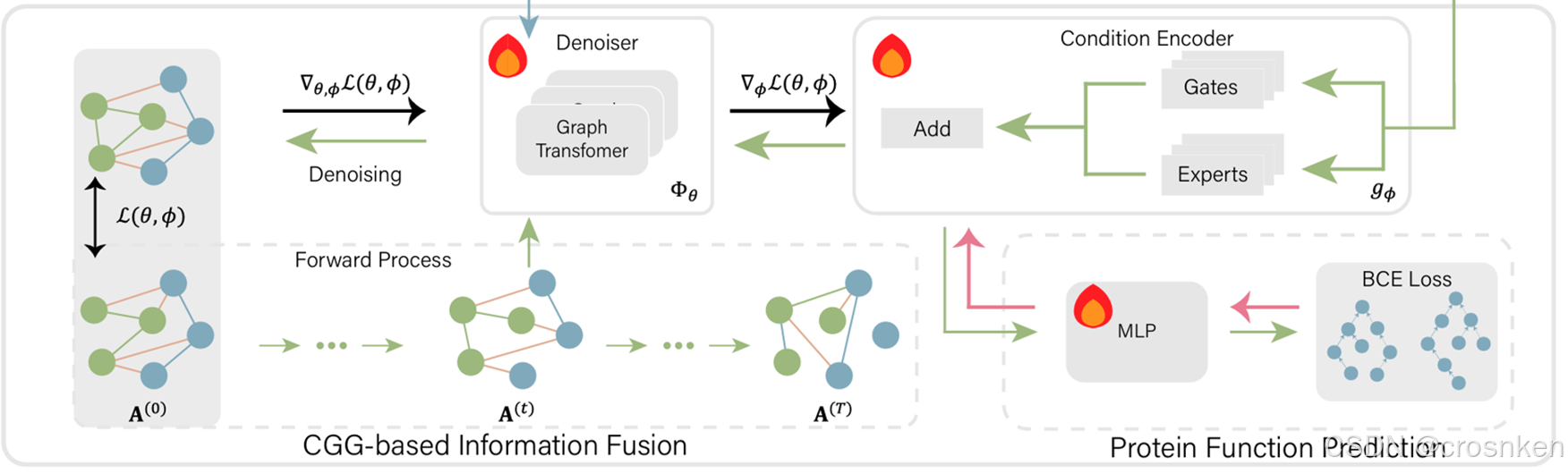
每个蛋白质取k跳内的子图,作为它的ego-graph,对ego-graph进行加噪与还原。
使用的是DiGress模型,通过一系列操作对异构图引入噪声(Forward Process),通过graph-transformer还原图中节点的类型,使用交叉熵损失训练。
虽然描述非常复杂,什么马尔可夫过程,条件图生成之类的,但其实就是加了一个对ego-graph去噪的学习任务。
4、其他
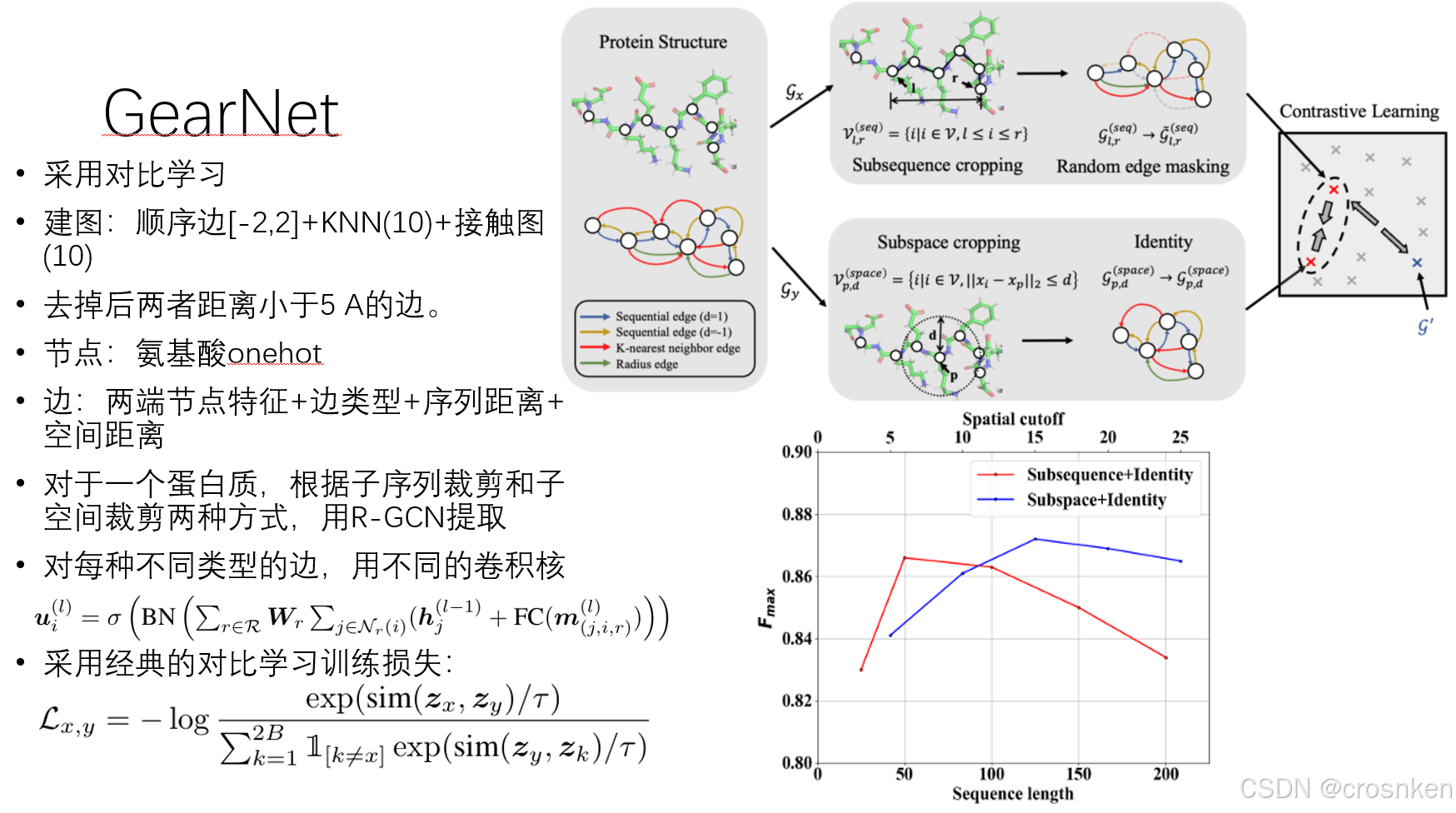
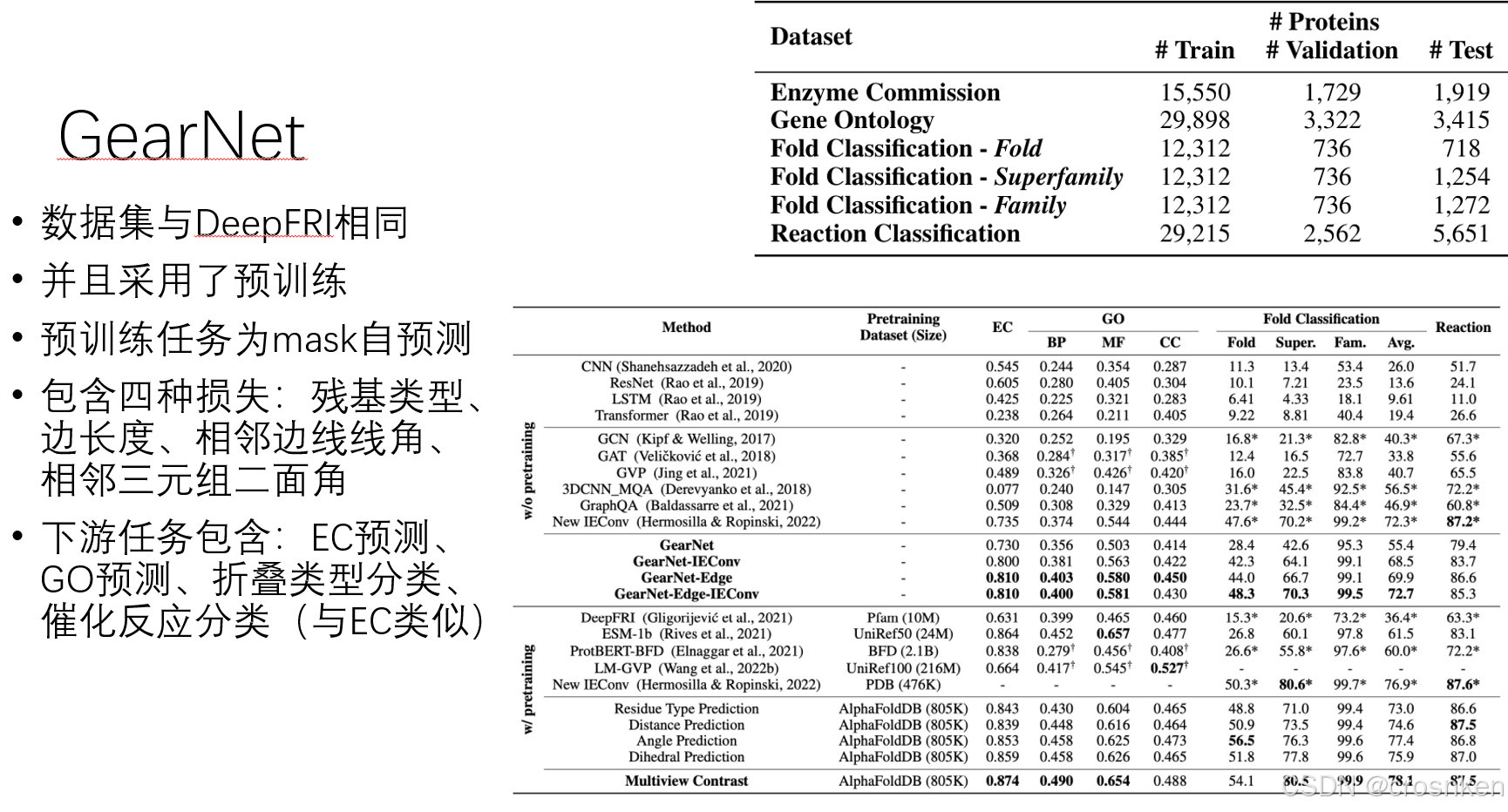
文中还提到了GearNet,不过它已经是比较老的结构模型了,和GVP差不多是一个时期的。
所以不打算展开讲了。放两张PPT
实验结果
对比实验
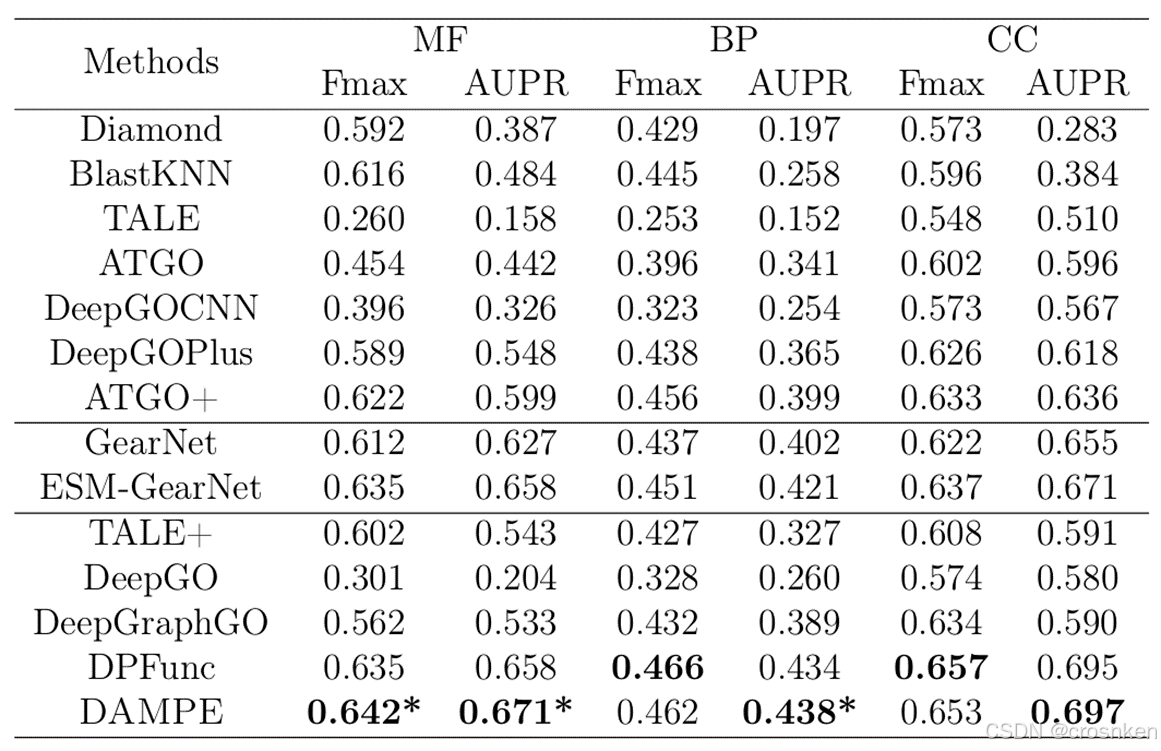
可以说是完完全全瞄着DPFunc出手的一篇文章,但DPFunc的论文指标其实是虚低的,实际跑起来会更高。
消融实验
先对特征对齐部分进行了消融实验
四种方法:直接拼接,对比学习(以同个蛋白质的seq和struct嵌入为正样本对,不同蛋白质间的嵌入为负样本对),交叉注意力,串行连接(类似DPFunc,将ESM2的输出作为GearNet的初始节点特征)
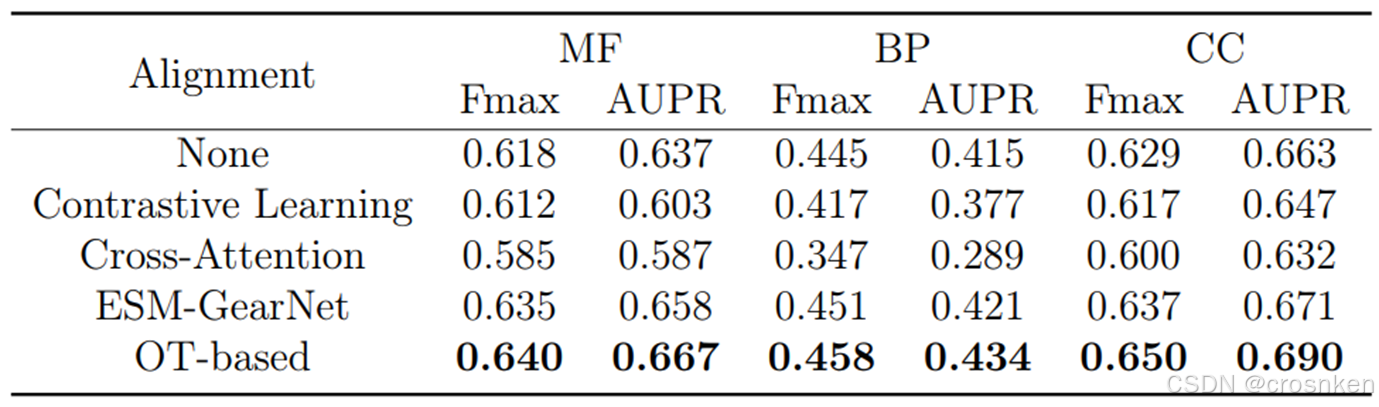
比较可惜的地方在于,没有做把OT换成可训练的MLP的实验。
然后对信息融合部分做了消融实验
三种方法:用GAT和SAGE融合PPI信息(把MoE换成GNN,在PPI图上卷积),不使用CGG方法,直接使用MoE。
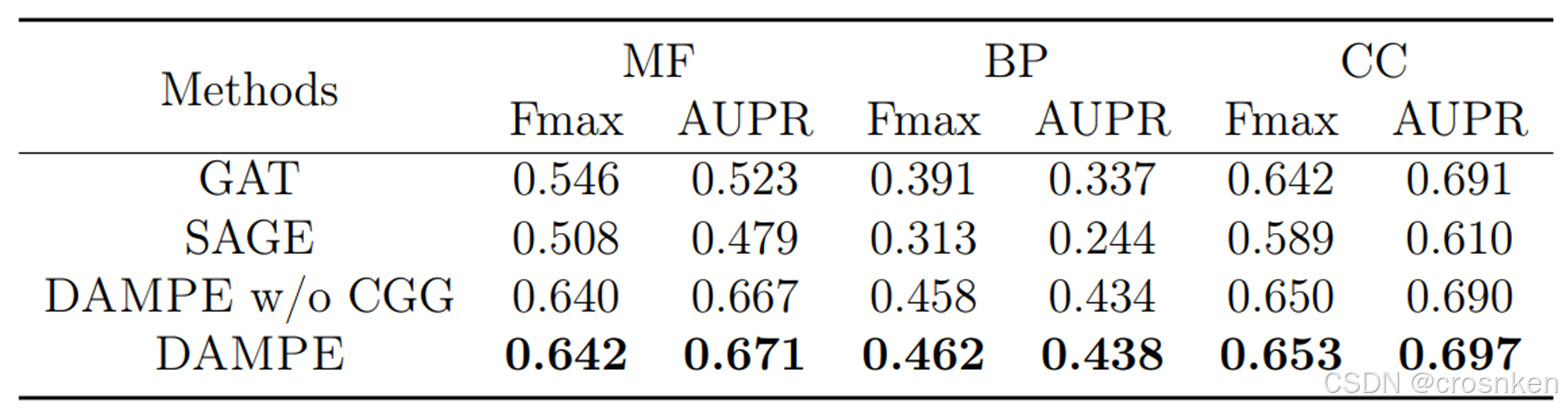
感觉用GraphTransformer做的CGG对结果的提升并不大,耗费大量运算资源,最终只提升0.004。
多任务训练可能还是对蛋白质功能预测任务存在一定的影响。如果能改进一下信息融合的过程,可能会有更好的结果。
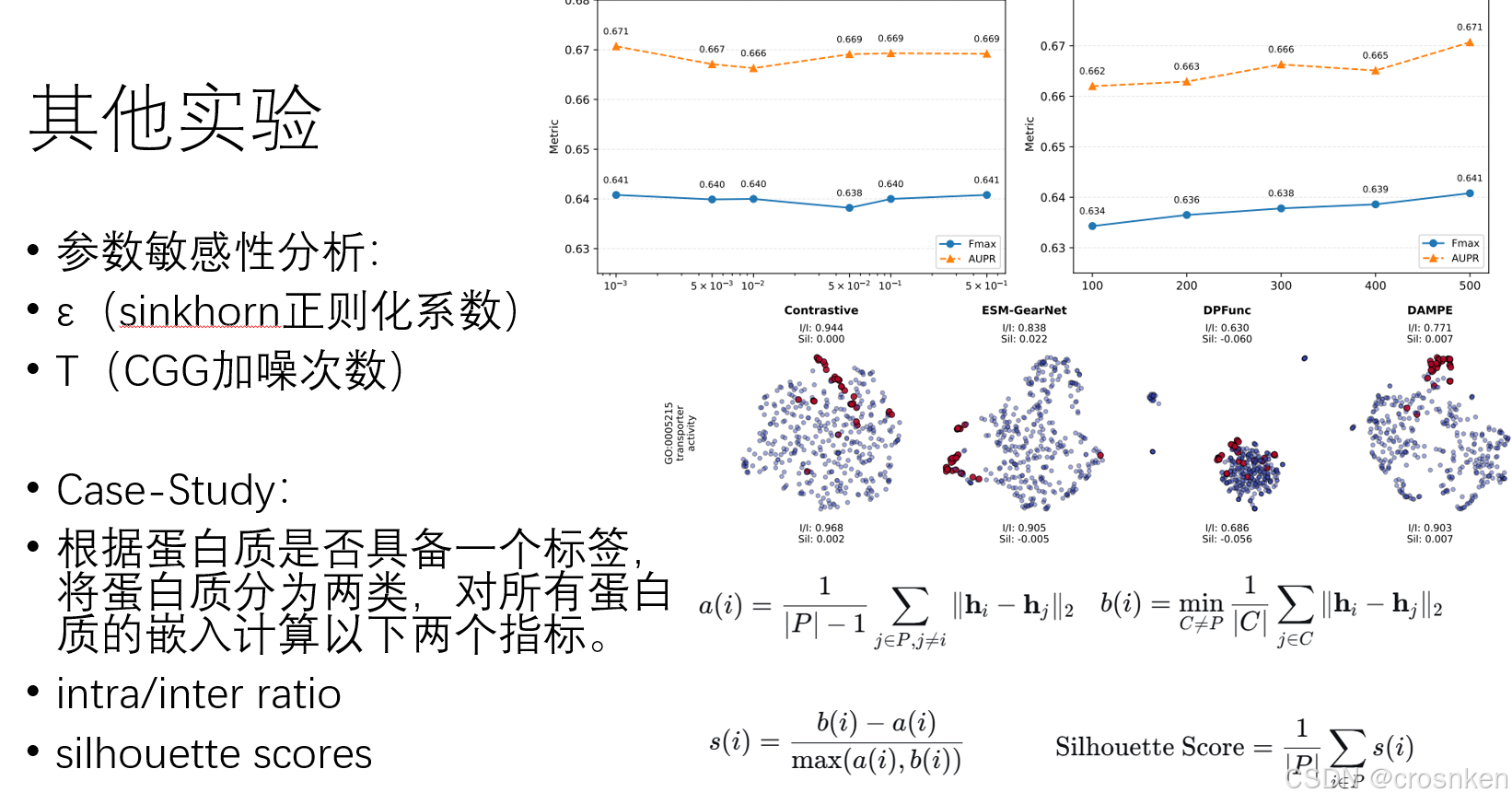
其他实验
还做了参数敏感性分析和具体案例分析的实验,不过不打算展开讲了。
放张PPT。
后记
这篇论文数学偏向更多一些,很多东西都与数学理论相关,读的时候可能需要了解很多数学背景。
论文全长30多页,内容非常多,如果有想要了解的细节,可以去看看论文原文。