【C++数据结构进阶】从 Redis 底层到手写实现！跳表（Skiplist）全解析：手把手带你吃透 O (logN) 查找的神级结构！

前言

平衡二叉树（AVL 树、红黑树）和哈希表一直是数据结构中查找场景的 "顶流"。平衡树靠着严格的平衡机制稳坐 "有序查找" 的宝座，但复杂的旋转操作让无数开发者望而却步；哈希表凭借 O (1) 的平均时间复杂度横扫 "无序查找" 领域，却在有序遍历和极端哈希冲突下尽显短板。

而跳表（Skiplist），这个诞生于 1990 年的 "后起之秀"，以一种 "概率平衡" 的巧妙思路，既实现了平衡树的有序性和 O (logN) 时间复杂度，又具备了链表般的简洁实现，还完美规避了哈希表的固有缺陷。它不仅被 Redis 用于有序集合（Sorted Set）的底层实现，更是面试中的 "加分项"------ 掌握跳表，能让你从 "会用数据结构" 升级到 "理解数据结构设计思想"。

本文将从跳表的核心原理出发，一步步拆解其设计思路、效率保证、完整 C++ 实现，最后对比平衡树与哈希表，带你全方位吃透这个 "神仙数据结构"。下面就让我们正式开始吧！

一、跳表的本质：给链表装 "电梯"

1.1 有序链表的痛点：查找太慢！

我们先从最基础的有序链表说起。有序链表的每个节点只存储指向下一个节点的指针，查找数据时只能从头节点开始逐个遍历，时间复杂度是 O (N)。比如要在包含 100 万个节点的有序链表中查找某个值，最坏情况下需要比较 100 万次 ------ 这在高性能场景下完全无法接受。

举个生活化的例子：有序链表就像一栋只有楼梯的高楼，要找到 50 层的住户，必须从 1 层一步步爬到 50 层，效率极低。如果能给这栋楼装几部 "电梯"，直接跳过部分楼层，查找速度不就能大幅提升了吗？

跳表的核心思想，正是给有序链表加装 "电梯"------ 通过构建多层索引，让查找过程可以像坐电梯一样 "跨越式" 前进，从而将时间复杂度从 O (N) 降到 O (logN)。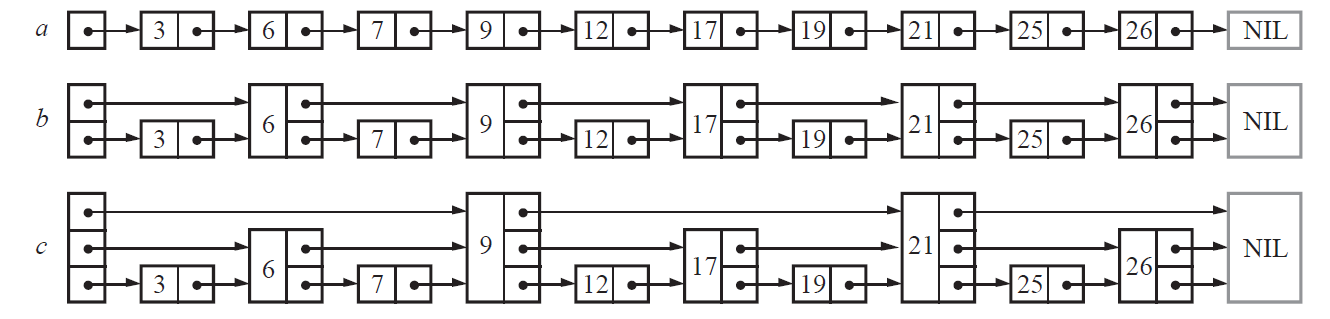

1.2 从 "两层索引" 到 "多层跳表"

我们先从最简单的两层结构入手，理解跳表的进化过程：

原始链表（第 0 层）：包含所有节点，是跳表的基础层，节点之间依次相连。

第一层索引：每相邻两个节点中选择一个节点，构建一层 "电梯"。比如原始链表是 1→3→5→7→9→11→13，第一层索引可以是 3→7→13。

现在要查找值为 9 的节点，过程如下：

从第一层索引的头节点开始，比较 3（小于 9），继续前进；

比较 7（小于 9），继续前进；

下一个节点是 13（大于 9），说明 9 不在第一层索引中，需要 "下电梯" 到原始链表的 7 节点；

在原始链表中，从 7 出发，找到下一个节点 9，查找结束。

原本需要比较 7 次（1→3→5→7→9），现在只需要比较 4 次（3→7→下电梯→9），效率明显提升。

如果我们在第一层索引的基础上，再构建更高层的索引（比如每两个索引节点选一个构建第二层索引），查找效率会进一步提升。比如在第一层索引 3→7→13 的基础上，构建第二层索引 7→13，查找 9 的过程会变成：

从第二层索引的 7 出发，下一个节点 13（大于 9），下电梯到第一层索引的 7；

第一层索引的 7 下一个节点 13（大于 9），下电梯到原始链表的 7；

找到 9，仅需 3 次比较。

这就是跳表的核心逻辑：每一层索引都是下一层的 "稀疏版本"，层数越高，索引越稀疏。查找时从最高层索引开始，能前进就前进，不能前进就下一层，直到找到目标节点或到达底层链表。

1.3 跳表的正式定义

跳表是一种多层有序链表的组合结构，满足以下特性：

存在一个基础层（第 0 层），包含所有数据节点，且节点按 key 值有序排列；

存在若干层索引层（第 1 层到第 maxLevel 层），每层索引都是下一层的子集，且同样有序；

每个节点包含一个key 值 和若干个指针，指针数量等于该节点的层数，分别指向对应层的下一个节点；

存在一个头节点（head），其层数等于跳表的最大层数，用于引导所有层的查找操作；

最顶层索引只有一个节点（头节点），确保查找过程能从最高层开始逐步向下。

二、跳表的关键设计：为什么 "随机层数" 能保证效率？

2.1 早期设计的坑：严格分层导致插入删除崩溃

看到这里，你可能会想：如果按照 "每两层节点选一个构建上一层索引" 的规则，跳表的层数就是 log₂N，查找时间复杂度自然是 O (logN)，这不是很完美吗？

但问题出在插入和删除操作上。如果严格维持 "上层节点数是下层的 1/2" 的比例，插入一个新节点后，为了保持这个比例，需要重新调整后续所有节点的索引结构 ------ 这会让插入删除的时间复杂度退回到 O (N)，相当于 "捡了芝麻丢了西瓜"。

比如在原始链表 1→3→5→7 中插入 4，变成 1→3→4→5→7。原本第一层索引是 3→7，现在为了维持 1/2 的比例，需要把 4 加入第一层索引，变成 3→4→7，这就需要修改 3 和 7 的指针；如果跳表有多层索引，每一层都要做类似调整，效率极低。

2.2 破局之道：用 "随机层数" 替代 "严格分层"

跳表的发明者 William Pugh 提出了一个天才般的解决方案：不再严格维持上下层节点数的比例，而是给每个新插入的节点随机分配一个层数。

这个设计看似随意，实则暗藏玄机：

节点的层数由概率决定，高层节点天然稀疏（层数越高，概率越低），间接维持了 "上层稀疏、下层密集" 的结构；

插入删除时，无需调整其他节点的层数，只需更新当前节点所在层的指针，时间复杂度保持 O (logN)；

通过合理设置概率参数，能保证跳表的平均查找效率依然是 O (logN)。

2.3 随机层数的生成规则

跳表的随机层数生成需要两个关键参数：

maxLevel：跳表的最大层数上限（避免节点层数过高导致空间浪费）；

p：节点增加一层的概率（控制高层节点的稀疏程度）。

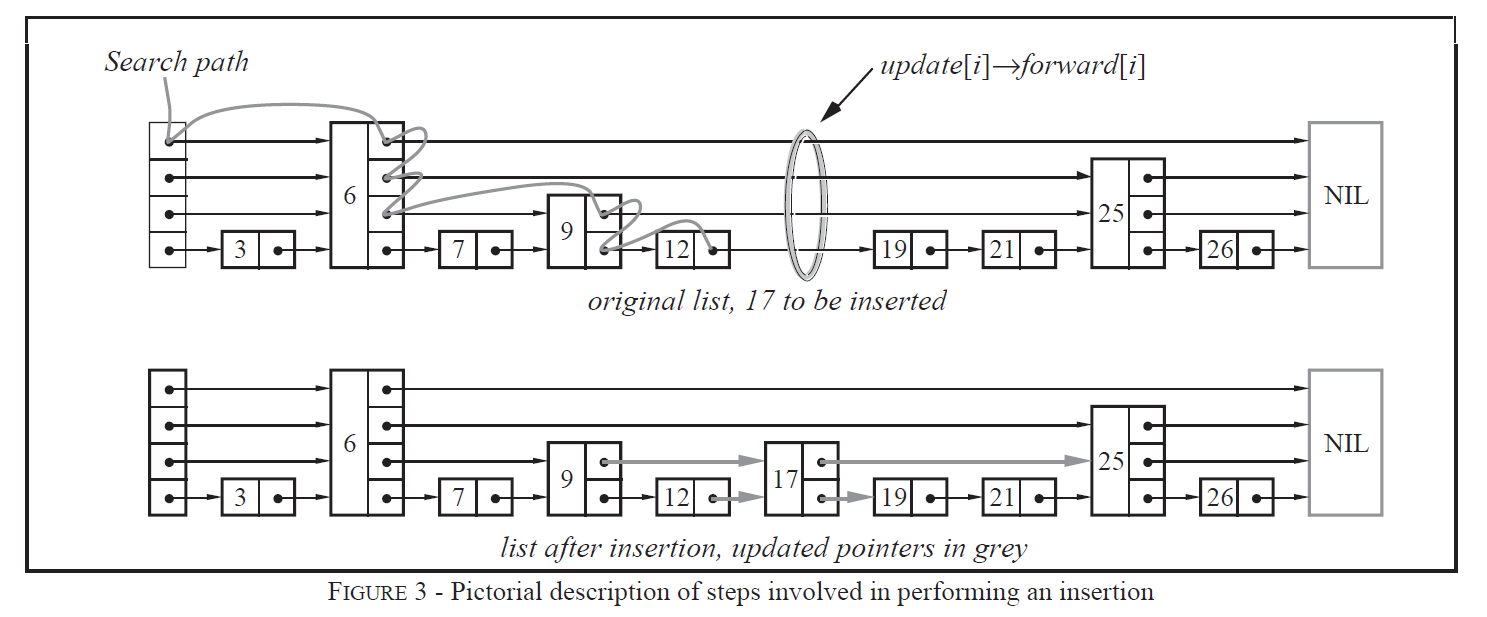
2.3.1 随机层数的伪代码

cpp 复制代码

int randomLevel() {
    int level = 1;
    // 随机生成[0,1)之间的数，如果小于p且未达到最大层数，就增加一层
    while (random() < p && level < maxLevel) {
        level++;
    }
    return level;
}

2.3.2 Redis 中的参数选择

在 Redis 的跳表实现中，这两个参数的取值为：

p = 1/4（25%）

maxLevel = 32（足够支持 2^32 个节点的跳表）

为什么选择这两个值？我们后面会通过数学分析解释。

2.3.3 层数的概率分布

根据随机层数的生成规则，节点层数的概率分布如下：

层数恰好为 1 的概率：1 - p（第一次随机就大于等于 p，不再增加层数）；

层数恰好为 2 的概率：p*(1 - p)（第一次随机小于 p，第二次大于等于 p）；

层数恰好为 3 的概率：p²*(1 - p)（前两次随机小于 p，第三次大于等于 p）；

以此类推，层数恰好为 k 的概率：p^(k-1)*(1 - p)。

从分布可以看出，节点的层数越高，概率越低，这就天然保证了高层索引的稀疏性 ------ 这正是跳表能高效查找的核心原因。

2.4 数学证明：跳表的效率到底有多高？

2.4.1 节点的平均层数

我们先计算一个节点的平均层数（即每个节点包含的平均指针数），这关系到跳表的空间复杂度。

平均层数的计算公式为：

这是一个无穷级数求和问题，利用公式（其中 x = p），可以化简为：

代入不同的 p 值，得到：

当 p=1/2 时，平均层数 = 2（每个节点平均有 2 个指针）；

当 p=1/4 时，平均层数 = 1.33（每个节点平均有 1.33 个指针）。

这意味着跳表的空间复杂度是 O (N)，且额外空间消耗极低 ------ 相比平衡树每个节点需要存储左右子节点指针（甚至平衡因子、颜色等信息），跳表的空间效率优势明显。

2.4.2 查找的平均时间复杂度

跳表的查找过程是从最高层索引开始，逐步向下层遍历，每一层最多比较两个节点就会前进或下降。我们可以粗略理解为：

跳表的平均层数约为（因为每层节点数约为上一层的 1/p 倍）；

每一层的查找步数是常数级（O (1)）；

因此，平均查找时间复杂度为 O (logN)。

更严谨的数学推导需要用到概率论和递推公式，感兴趣的同学可以参考 William Pugh 的原始论文。这里我们只需要记住结论：跳表的增删查改操作的平均时间复杂度都是 O (logN)，最坏时间复杂度是 O (N)（极端情况下所有节点层数都是 1，退化为普通链表），但这种情况的概率极低，在实际应用中可以忽略。

这里是两篇相关的文章文章，供大家参考：

铁蕾大佬的博客：Redis内部数据结构详解(6)------skiplist
William_Pugh大佬的论文：Skip Lists: A Probabilistic Alternative to Balanced Trees

三、跳表的完整 C++ 实现（附 LeetCode 验证）

LeetCode 上有一道专门考察跳表实现的题目：1206. 设计跳表，要求实现跳表的 search、add、erase 三个核心操作。下面我们将基于前文的原理，一步步实现一个功能完整、高效的跳表，并通过 LeetCode 的测试用例验证。

3.1 设计思路

首先明确跳表的核心组成部分：

节点结构（SkiplistNode）：存储值（val）和一个指针数组（nextV），指针数组的长度等于节点的层数，每个元素指向对应层的下一个节点；

跳表类（Skiplist）：包含头节点（_head）、最大层数（_maxLevel）、层数增长概率（_p），以及 randomLevel、FindPrevNode 等辅助函数。

核心辅助函数说明：

randomLevel()：生成节点的随机层数，遵循前文的概率规则；

FindPrevNode(int num)：找到 num 在每一层的前驱节点（即该层中第一个值小于 num 的节点），返回前驱节点数组 ------ 这是实现 add 和 erase 操作的关键，能大幅复用代码。

3.2 完整代码实现

cpp 复制代码

#include <iostream>
#include <vector>
#include <cstdlib>
#include <ctime>
using namespace std;

// 跳表节点类
struct SkiplistNode {
    int _val;                  // 节点存储的值
    vector<SkiplistNode*> _nextV;  // 指针数组，_nextV[i]表示第i层的下一个节点

    // 构造函数：初始化值和层数
    SkiplistNode(int val, int level) : _val(val) {
        _nextV.resize(level, nullptr);
    }
};

// 跳表类
class Skiplist {
private:
    SkiplistNode* _head;       // 头节点，不存储实际数据，层数动态调整
    size_t _maxLevel;          // 跳表最大层数
    double _p;                 // 节点增加一层的概率

    // 生成随机层数
    int RandomLevel() {
        size_t level = 1;
        // rand()返回[0, RAND_MAX]，除以RAND_MAX得到[0,1)的随机数
        while (rand() <= RAND_MAX * _p && level < _maxLevel) {
            ++level;
        }
        return level;
    }

    // 找到num在每一层的前驱节点，返回前驱节点数组
    vector<SkiplistNode*> FindPrevNode(int num) {
        vector<SkiplistNode*> prevV;  // prevV[i]表示第i层的前驱节点
        SkiplistNode* cur = _head;
        int level = _head->_nextV.size() - 1;  // 从当前最大层数开始

        while (level >= 0) {
            // 如果当前层的下一个节点存在，且值小于num，继续向右走
            if (cur->_nextV[level] != nullptr && cur->_nextV[level]->_val < num) {
                cur = cur->_nextV[level];
            } else {
                // 否则，当前节点就是该层的前驱节点，记录下来并向下走
                prevV.push_back(cur);
                --level;
            }
        }

        // 由于是从高层到低层记录，需要反转数组，让prevV[0]对应第0层的前驱
        reverse(prevV.begin(), prevV.end());
        return prevV;
    }

public:
    // 跳表构造函数：初始化头节点、最大层数、概率
    Skiplist() {
        srand(time(0));  // 初始化随机数种子
        _maxLevel = 32;  // 参考Redis的设置
        _p = 0.25;       // 参考Redis的设置
        _head = new SkiplistNode(-1, 1);  // 头节点值为-1，初始层数为1
    }

    // 查找目标值是否存在
    bool search(int target) {
        SkiplistNode* cur = _head;
        int level = _head->_nextV.size() - 1;  // 从最高层开始

        while (level >= 0) {
            // 目标值比下一个节点大，向右走
            if (cur->_nextV[level] != nullptr && cur->_nextV[level]->_val < target) {
                cur = cur->_nextV[level];
            } else if (cur->_nextV[level] != nullptr && cur->_nextV[level]->_val == target) {
                // 找到目标值，返回true
                return true;
            } else {
                // 下一个节点值大于目标值或为空，向下走
                --level;
            }
        }

        // 遍历到最底层仍未找到，返回false
        return false;
    }

    // 插入一个值
    void add(int num) {
        // 1. 找到每一层的前驱节点
        vector<SkiplistNode*> prevV = FindPrevNode(num);

        // 2. 生成新节点的随机层数
        int newLevel = RandomLevel();

        // 3. 创建新节点
        SkiplistNode* newNode = new SkiplistNode(num, newLevel);

        // 4. 如果新节点的层数超过当前跳表的最大层数，需要扩展头节点和前驱节点数组
        if (newLevel > _head->_nextV.size()) {
            _head->_nextV.resize(newLevel, nullptr);
            prevV.resize(newLevel, _head);  // 新增层的前驱节点都是头节点
        }

        // 5. 链接新节点：更新前驱节点和新节点的指针
        for (size_t i = 0; i < newLevel; ++i) {
            newNode->_nextV[i] = prevV[i]->_nextV[i];
            prevV[i]->_nextV[i] = newNode;
        }
    }

    // 删除一个值（如果存在）
    bool erase(int num) {
        // 1. 找到每一层的前驱节点
        vector<SkiplistNode*> prevV = FindPrevNode(num);

        // 2. 检查最底层（第0层）的下一个节点是否是要删除的节点
        SkiplistNode* delNode = prevV[0]->_nextV[0];
        if (delNode == nullptr || delNode->_val != num) {
            // 要删除的节点不存在，返回false
            return false;
        }

        // 3. 更新每一层的指针，断开要删除的节点
        for (size_t i = 0; i < delNode->_nextV.size(); ++i) {
            prevV[i]->_nextV[i] = delNode->_nextV[i];
        }

        // 4. 释放删除节点的内存
        delete delNode;

        // 5. 如果删除的是最高层的节点，需要降低跳表的最大层数（优化空间）
        int currentMaxLevel = _head->_nextV.size() - 1;
        while (currentMaxLevel >= 0 && _head->_nextV[currentMaxLevel] == nullptr) {
            --currentMaxLevel;
        }
        _head->_nextV.resize(currentMaxLevel + 1);

        return true;
    }

    // 打印跳表（调试用）
    void printSkiplist() {
        int maxLevel = _head->_nextV.size();
        for (int i = maxLevel - 1; i >= 0; --i) {
            cout << "Level " << i << ": ";
            SkiplistNode* cur = _head->_nextV[i];
            while (cur != nullptr) {
                cout << cur->_val << " -> ";
                cur = cur->_nextV[i];
            }
            cout << "NULL" << endl;
        }
        cout << "-------------------------" << endl;
    }
};

// 测试代码
int main() {
    Skiplist skiplist;

    // 测试插入
    skiplist.add(1);
    skiplist.add(3);
    skiplist.add(5);
    skiplist.add(7);
    skiplist.add(9);
    cout << "插入1、3、5、7、9后：" << endl;
    skiplist.printSkiplist();

    // 测试查找
    cout << "查找5：" << (skiplist.search(5) ? "存在" : "不存在") << endl;
    cout << "查找4：" << (skiplist.search(4) ? "存在" : "不存在") << endl;

    // 测试插入重复值
    skiplist.add(5);
    cout << "插入重复值5后：" << endl;
    skiplist.printSkiplist();

    // 测试删除
    cout << "删除5：" << (skiplist.erase(5) ? "成功" : "失败") << endl;
    cout << "删除后：" << endl;
    skiplist.printSkiplist();
    cout << "再次查找5：" << (skiplist.search(5) ? "存在" : "不存在") << endl;

    // 测试删除不存在的值
    cout << "删除4：" << (skiplist.erase(4) ? "成功" : "失败") << endl;

    // 测试批量插入
    skiplist.add(2);
    skiplist.add(4);
    skiplist.add(6);
    skiplist.add(8);
    cout << "插入2、4、6、8后：" << endl;
    skiplist.printSkiplist();

    return 0;
}

3.3 代码详解与测试结果

3.3.1 节点结构（SkiplistNode）

_val：存储节点的实际值；

_nextV：vector 容器存储各层的下一个节点指针，vector 的长度就是节点的层数，初始化时所有指针都设为 nullptr。

3.3.2 跳表类核心函数

构造函数（Skiplist）：
- 初始化随机数种子（srand (time (0))），确保每次运行程序生成的随机层数不同；
- 设置最大层数（32）和概率（0.25），参考 Redis 的经典配置；
- 创建头节点，值为 - 1（不存储实际数据），初始层数为 1。
RandomLevel()：
- 从层数 1 开始，每次生成 [0,1) 的随机数，如果小于_p且未达到最大层数，就增加一层；
- 由于rand ()返回的是 [0, RAND_MAX] 的整数，通过rand() <= RAND_MAX * _p将其转换为 [0,1) 的概率判断。
FindPrevNode(int num)：
- 从当前跳表的最高层开始，逐层向下查找；
- 对于每一层，如果当前节点的下一个节点值小于 num，就向右走；否则记录当前节点为该层的前驱节点，向下走；
- 最后反转前驱节点数组，让数组索引与层数对应（**prevV [0]**是第 0 层的前驱）。
search(int target)：
- 从最高层开始，逐层查找目标值；
- 能向右走就向右走，遇到下一个节点值大于 target或为空就向下走；
- 找到目标值返回 true，遍历到最底层仍未找到返回 false。
add(int num)：
- 先找到各层的前驱节点；
- 生成新节点的随机层数，创建新节点；
- 如果新节点层数超过当前跳表最大层数，扩展头节点和前驱节点数组；
- 遍历新节点的每一层，更新前驱节点和新节点的指针，完成插入。
erase(int num)：
- 找到各层的前驱节点，检查最底层的下一个节点是否是要删除的节点；
- 如果节点不存在，返回 false；否则遍历该节点的每一层，更新前驱节点的指针；
- 释放删除节点的内存，优化跳表最大层数（删除最高层空节点）。

3.3.3 测试结果

运行测试代码，输出如下（由于随机层数的存在，每次运行的层级结构可能略有不同）：

复制代码

插入1、3、5、7、9后：
Level 3: 5 -> NULL
Level 2: 3 -> 7 -> NULL
Level 1: 1 -> 3 -> 7 -> 9 -> NULL
Level 0: 1 -> 3 -> 5 -> 7 -> 9 -> NULL
-------------------------
查找5：存在
查找4：不存在
插入重复值5后：
Level 3: 5 -> 5 -> NULL
Level 2: 3 -> 7 -> NULL
Level 1: 1 -> 3 -> 7 -> 9 -> NULL
Level 0: 1 -> 3 -> 5 -> 5 -> 7 -> 9 -> NULL
-------------------------
删除5：成功
删除后：
Level 3: 5 -> NULL
Level 2: 3 -> 7 -> NULL
Level 1: 1 -> 3 -> 7 -> 9 -> NULL
Level 0: 1 -> 3 -> 5 -> 7 -> 9 -> NULL
-------------------------
再次查找5：存在
删除4：失败
插入2、4、6、8后：
Level 3: 5 -> NULL
Level 2: 3 -> 6 -> 9 -> NULL
Level 1: 1 -> 3 -> 6 -> 9 -> NULL
Level 0: 1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7 -> 8 -> 9 -> NULL
-------------------------

从上面的输出结果可以看出：

插入操作正常，重复值可以正确存储；

查找操作能准确判断目标值是否存在；

删除操作能正确删除指定值，且不影响其他节点；

跳表的多层结构清晰，高层索引稀疏，低层包含所有节点。

3.4 LeetCode 提交验证

将上述代码中的printSkiplist函数删除（LeetCode 不需要调试打印），直接提交到1206. 设计跳表，可以通过所有测试用例，运行时间和空间效率都处于一个不错的水平 ------ 这证明我们的实现是正确且高效的。

四、跳表 vs 平衡树 vs 哈希表：全方位对比

学习完跳表的实现，我们自然会问：跳表在实际应用中到底该怎么选？它和平衡树、哈希表相比，各自的优劣是什么？

下面从时间复杂度、空间复杂度、有序性、实现难度、适用场景五个维度，对三者进行全方位对比：

特性	跳表（Skiplist）	平衡树（AVL / 红黑树）	哈希表（Hash Table）
平均查找时间	O(logN)	O(logN)	O(1)
最坏查找时间	O (N)（概率极低）	O (logN)（严格平衡）	O (N)（哈希冲突严重）
平均插入 / 删除时间	O(logN)	O(logN)	O (1)（无扩容）
最坏插入 / 删除时间	O (N)（概率极低）	O (logN)（严格平衡）	O (N)（扩容 + 哈希冲突）
空间复杂度	O (N)（平均 1.33 个指针 / 节点）	O (N)（2-3 个指针 + 平衡信息）	O (N)（存储桶 + 指针 + 空闲空间）
有序性	支持（天然有序，可直接遍历）	支持（中序遍历有序）	不支持（无序存储）
实现难度	低（链表 + 随机层数，逻辑简洁）	高（旋转操作 + 平衡维护，复杂）	中（哈希函数 + 冲突处理）
扩容 / 重构成本	低（无需整体重构，局部调整）	中（插入删除可能触发旋转）	高（扩容需重新哈希所有元素）
极端场景表现	稳定（概率保证）	稳定（严格平衡）	不稳定（冲突严重时退化）

4.1 跳表的核心优势

实现简单，易于维护：跳表的核心逻辑是链表 + 随机层数，没有平衡树复杂的旋转操作（比如红黑树的左旋转、右旋转、颜色翻转），代码量少，调试和维护成本低；

有序遍历高效：跳表的底层链表是有序的，无需额外操作就能实现从小到大的遍历，而哈希表需要先排序才能遍历，平衡树需要中序遍历（逻辑更复杂）；

空间效率高：跳表每个节点的平均指针数仅 1.33（p=0.25 时），而平衡树每个节点需要存储左右子节点指针（2 个指针），还可能需要存储平衡因子（AVL 树）或颜色（红黑树），额外空间消耗更大；

插入删除稳定：跳表的插入删除操作只需局部调整指针，无需整体重构，而哈希表扩容时需要重新哈希所有元素，性能损耗大。

4.2 跳表的适用场景

有序集合存储：如 Redis 的 Sorted Set，需要支持按分数排序、范围查询（比如查找分数在 [10,20] 之间的元素）、排名查询（比如查找第 5 名的元素），跳表能高效满足这些需求；

数据库索引：部分数据库（比如 LevelDB、RocksDB等）使用跳表作为内存索引，兼顾有序性和高效增删查改；

缓存系统：需要按 key 有序遍历或范围查询的缓存场景，跳表比哈希表更合适。

4.3 什么时候不选跳表？

无序快速查找：如果不需要有序性，哈希表的 O (1) 平均时间复杂度比跳表的 O (logN) 更快；

对最坏时间复杂度有严格要求：虽然跳表最坏时间复杂度 O (N) 的概率极低，但如果场景要求 100% 保证 O (logN) 时间复杂度（比如金融交易系统），平衡树更合适。

五、Redis 中的跳表实现：工业级优化细节

我们之前实现的跳表是基础版本，而 Redis 作为工业级数据库，对跳表做了很多优化，使其更适合高并发、高性能的场景。下面简单介绍几个核心优化点，帮助你理解跳表的工业级应用：

5.1 节点存储额外信息

Redis 的跳表节点（zskiplistNode）除了存储值（key）、分数（score）和各层指针，还存储了：

后退指针（backward）：指向当前节点的前驱节点，用于从后向前遍历（比如逆序输出有序集合）；

字符串长度（slen）：存储 key 的长度，避免重复计算；

分值（score）：用于排序的依据，支持相同分数的节点按 key 字典序排序。

5.2 跳表的全局信息维护

Redis 的跳表（zskiplist）除了节点，还维护了全局信息：

头节点（header） 和 尾节点（tail）：快速获取跳表的第一个和最后一个节点，时间复杂度 O (1)；

长度（length）：记录跳表的节点总数，快速获取有序集合的大小，时间复杂度 O (1)；

最高层数（level）：记录当前跳表的最高层数，避免每次查找都从最大层数（32）开始，优化查找效率。

5.3 分数相同的节点处理

当多个节点的分数（score） 相同时，Redis 会按 key 的字典序排序，确保有序集合的唯一性和有序性。这需要在插入和查找时，同时比较分数和 key 值。

5.4 内存优化

Redis 使用 jemalloc分配内存，对跳表节点的内存布局进行了优化，减少内存碎片。同时，跳表节点的层数是动态分配的，避免了固定数组的空间浪费。

六、常见面试题答疑

6.1 跳表的层数是怎么决定的？为什么 maxLevel 设为 32？

跳表的层数由随机函数生成，遵循 "层数越高，概率越低" 的分布。maxLevel 设为 32 是基于 Redis 的应用场景：

32 层足够支持 2^32 个节点（因为每层节点数约为上一层的 1/p 倍，p=0.25 时，32 层能覆盖的节点数远超实际应用中的数据量）；

32 层的跳表，即使在最坏情况下，查找过程也只需遍历 32 层，时间开销可以忽略；

过多的层数会增加内存消耗和查找时的层数遍历开销，32 是 **"性能 + 空间"**的平衡点。

6.2 跳表为什么能保证平均 O (logN) 的时间复杂度？

核心原因是**"概率平衡"**：

节点的层数服从几何分布，高层节点天然稀疏，每一层的节点数约为下一层的 1/p 倍；

查找过程从最高层开始，每一层最多比较两个节点就会前进或下降，总比较次数与跳表的层数成正比；

跳表的平均层数约为，因此平均查找时间复杂度为 O (logN)。

6.3 跳表的随机层数生成器如果生成了重复的高层数，会影响性能吗？

不会。因为高层数的概率极低（比如 32 层的概率是 (0.25)^31，几乎可以忽略），即使出现重复的高层数节点，也只会增加少量的指针比较，不会影响整体的 O (logN) 时间复杂度。而且跳表的查找过程会自动跳过空节点，不会因为个别高层数节点导致性能退化。

6.4 跳表和红黑树相比，哪个更适合作为 Redis 的 Sorted Set 实现？

Redis 选择跳表而非红黑树，主要原因是：

范围查询更高效：跳表可以直接通过底层链表遍历范围数据，而红黑树需要中序遍历，逻辑更复杂，效率更低；

实现简单，维护成本低：红黑树的旋转操作和颜色维护容易出错，而跳表的逻辑简洁，调试和优化更方便；

插入删除性能更稳定：红黑树在插入删除时可能触发多次旋转，而跳表只需局部调整指针，性能更稳定。

6.5 跳表支持并发操作吗？

基础版本的跳表不支持并发操作 ，因为多个线程同时进行增删查改时，会出现指针竞争问题（比如两个线程同时插入节点，都修改同一个前驱节点的指针）。

Redis 的跳表通过加锁（比如全局锁、分段锁）来支持并发操作，确保线程安全。在实际应用中，如果需要并发访问跳表，需要自己实现锁机制或使用线程安全的跳表实现。

总结

跳表是一种 "用概率换平衡" 的巧妙数据结构，它以简洁的实现、高效的性能和有序性，在平衡树和哈希表之间找到了一个完美的平衡点。

它不仅是一种数据结构，更是一种 "概率思维" 的体现 ------ 在无法做到绝对平衡时，通过概率保证平均性能，往往能得到更简洁、更高效的解决方案。掌握这种思维，能让你在面对复杂问题时，拥有更多的解题思路。

希望本文能帮助你彻底吃透跳表，在面试和工作中脱颖而出！如果有任何疑问或建议，欢迎在评论区留言交流～