算法【c++】二叉树搜索树转换成排序双向链表

专栏前言：
在学习算法的时候，我刷一些算法题可以从大语言模型得到答案，但记不住，所以出这个专栏来完成自己对算法题目的感悟。也希望大家能有所收获。

主要简介：

个人主页：爱装代码的小瓶子
 算法专栏：你的算法难题小助手
 cpp编程语言详解
 操作系统详解--Linux

本文目录

描述
思路：
代码如下：

二叉搜索树与双向链表_牛客题霸_牛客网

描述

输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的双向链表。如下图所示

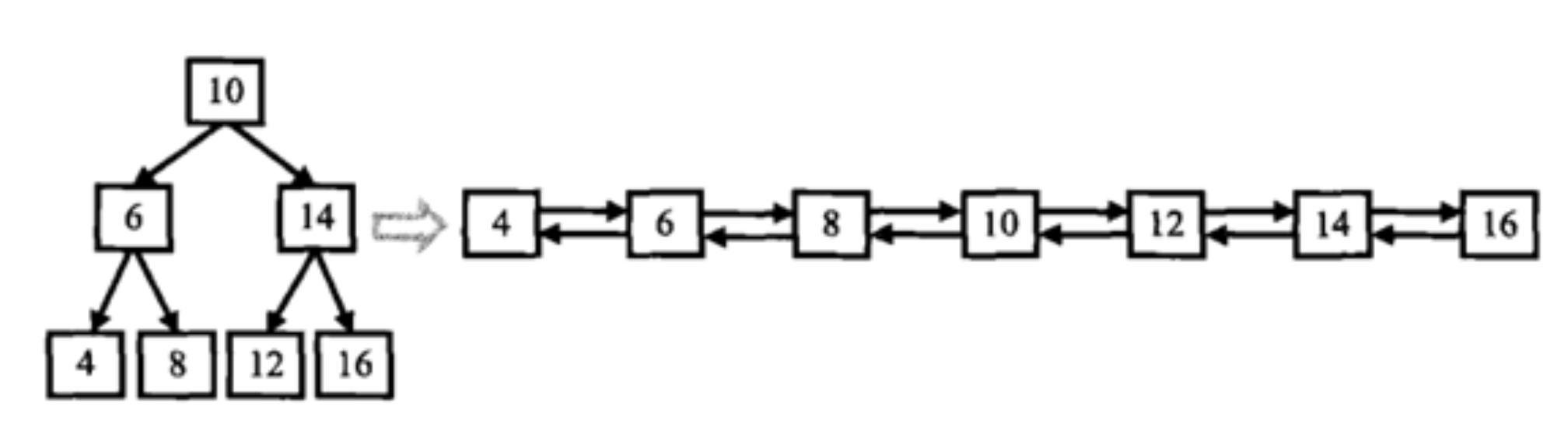
数据范围：输入二叉树的节点数 0≤n≤10000≤n≤1000，二叉树中每个节点的值 0≤val≤10000≤val≤1000

要求：空间复杂度O(1)O(1)（即在原树上操作），时间复杂度 O(n)O(n)

注意:

1.要求不能创建任何新的结点，只能调整树中结点指针的指向。当转化完成以后，树中节点的左指针需要指向前驱，树中节点的右指针需要指向后继

2.返回链表中的第一个节点的指针

3.函数返回的TreeNode，有左右指针，其实可以看成一个双向链表的数据结构

4.你不用输出双向链表，程序会根据你的返回值自动打印输出

双向链表的其中一个头节点。

思路：

这个题目指的是把二叉树转换成为双向链表，还要求不能开辟节点。那么就要在树上做文章了。

我们来看是以怎么样的规则来转换成为链表的，从小到大，而前符合二叉搜索树的中序遍历，那么我们只要在中序遍历的时候来完成链表的转换就可以了。（树中节点的左指针需要指向前驱，树中节点的右指针需要指向后继）

这是要求，那么还需要定义一个prev来记录（目前节点）cur的上一个节点。

cpp 复制代码

TreeNode* prev;//定义先前的节点，这里就记录了上一个节点.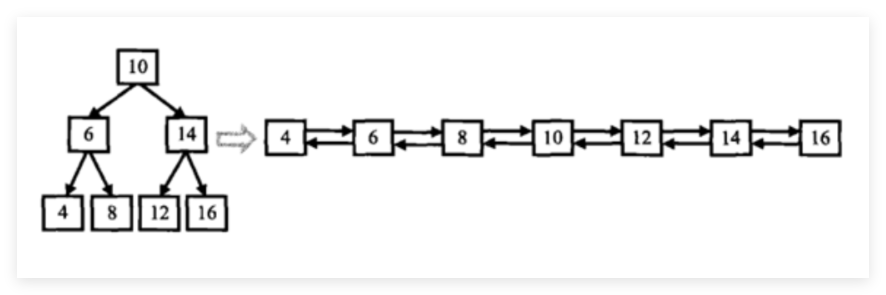

第一个节点是什么？答案是根节点的最左边（这就是最小的），我们应该怎么找的,用while吗，那应该怎么调整呢？实在太麻烦了，其实可以用递归，我在这个题目的理解就是先递出去，在回来的路上处理：

第一步：确定递归回归的条件，在这里节点为空就回来。配合下面几步大有作用。
第二步：先遍历左子树，由于第一个条件才开始放回，他会找到最小的（即我们需要的第一个节点，称为head）找到了应该做什么：left直接连接prev ，如果prev不为空，prev->left = cur.
第三步：这是cur的已经连接了前面，但是右边如果有节点，就需要往右走。（这里cur 相当于左中右的中）如果没有由于第一步的设置，他会往上递归，此时cur变成了需要指向的方向，prev还记录了前一个，通过如此递归便可以完成对整个树的遍历。

代码如下：

cpp 复制代码

class Solution {
public:
    TreeNode* prev;//定义先前的节点，这里就记录了上一个节点.
    void Inorder(TreeNode* cur){
        if(cur == nullptr) return;
        Inorder(cur->left);
        //当你到这一步了，其实已经是最左边的节点了:
        cur->left = prev;
        if(prev){
            prev->right = cur;
        }
        prev = cur;
        //此时cur的左边其实没数的，如果右边有数就玩下走，左中右，cur相当于中间
        //此时可以向上递归
        Inorder(cur->right);        
    }

    TreeNode* Convert(TreeNode* pRootOfTree) {
        if(pRootOfTree == nullptr) return nullptr;
        Inorder(pRootOfTree);
        auto head = pRootOfTree;
        while(head->left){
            head =  head->left;
        }
        return head;
    }
};

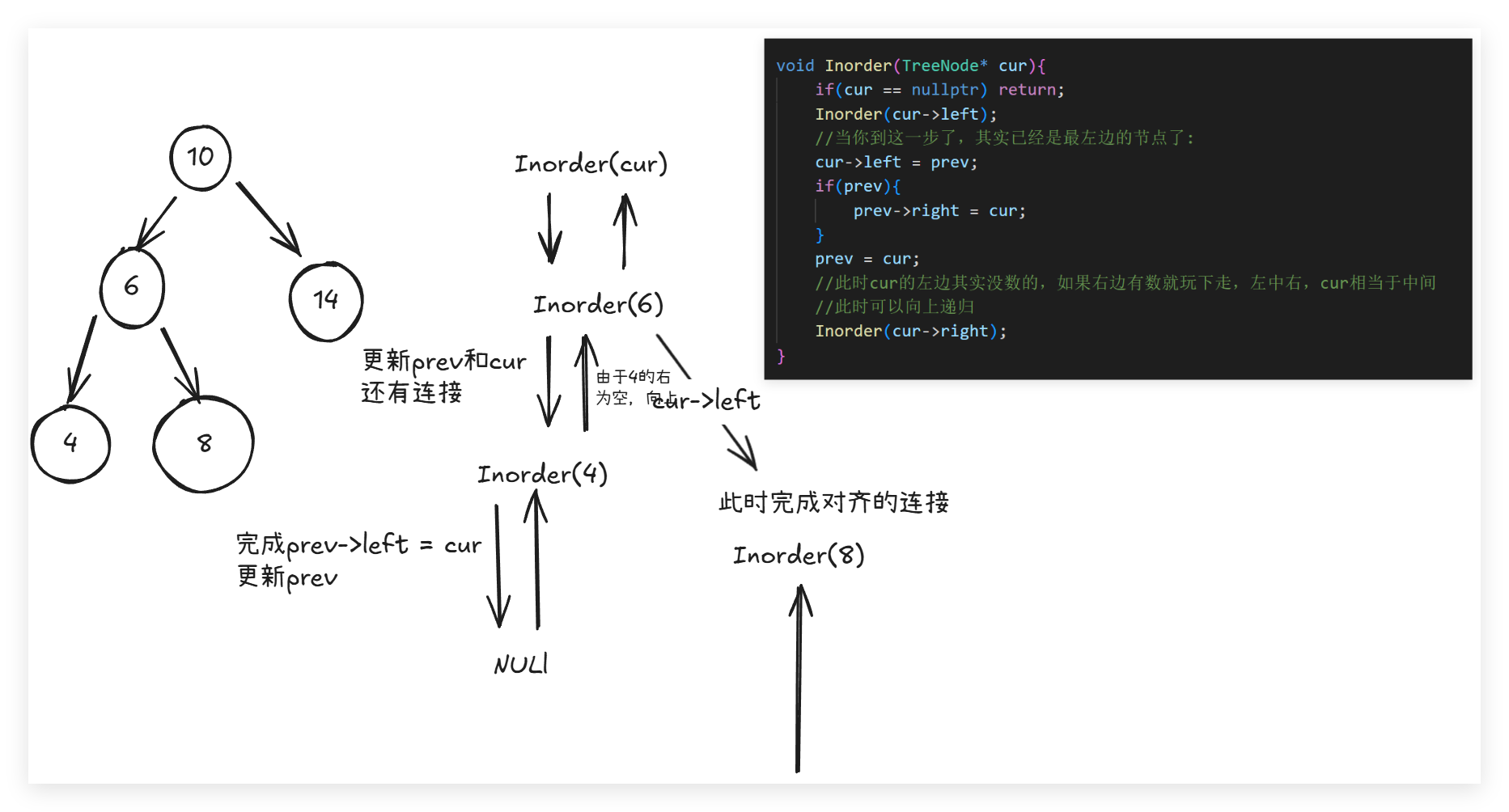
在这里就是在递归的时候进行处理，这种感觉就像水流一样，直至底部开始放回，在返回或者进行的时候对里面的链表进行处理。