LeetCode 840.矩阵中的幻方：模拟（+小小位运算）

【LetMeFly】840.矩阵中的幻方：模拟（+小小位运算）

力扣题目链接：https://leetcode.cn/problems/magic-squares-in-grid/

3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵，其中每行，每列以及两条对角线上的各数之和都相等。

给定一个由整数组成的row x col 的 grid，其中有多少个 3 × 3 的 "幻方" 子矩阵？

注意：虽然幻方只能包含 1 到 9 的数字，但 grid 可以包含最多15的数字。

示例 1：

复制代码

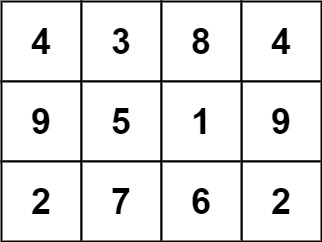
输入: grid = [[4,3,8,4],[9,5,1,9],[2,7,6,2]
输出: 1
解释: 
下面的子矩阵是一个 3 x 3 的幻方：

而这一个不是：

总的来说，在本示例所给定的矩阵中只有一个 3 x 3 的幻方子矩阵。

示例 2:

复制代码

输入: grid = [[8]]
输出: 0

提示:

row == grid.length
col == grid[i].length
1 <= row, col <= 10
0 <= grid[i][j] <= 15

解题方法：模拟

主函数中枚举每个3x3矩阵的右下角下表，写一个辅助函数计算右下角坐标为(i, j)的矩阵是否是幻方。

这个函数怎么写呢？

对于是否由1-9组成，可以使用位运算，将所有数与初始值为0的mask按位或，如出现3则 m a s k ∣ = 1 < < 3 mask |= 1 << 3 mask∣=1<<3，最终看 m a s k mask mask是否为 1 < < 10 − 2 1<<10-2 1<<10−2。

我们还可以使用两个大小为3的数组分别记录每一行和每一列的和，看他们是否相等、以及是否和主对角线和副对角线的和相等。

时间复杂度 O ( c o l × r o w ) O(col\times row) O(col×row)
空间复杂度 O ( 1 ) O(1) O(1)

AC代码

C++

cpp 复制代码

/*
 * @LastEditTime: 2025-12-30 13:25:00
 */
class Solution {
private:
    inline bool is(vector<vector<int>>& grid, int i, int j) {
        int mask = 0;
        int rowCnt[3] = {0}, colCnt[3] = {0};
        for (int di = 0; di < 3; di++) {
            for (int dj = 0; dj < 3; dj++) {
                int v = grid[i - di][j - dj];
                mask |= 1 << v;
                rowCnt[di] += v;
                colCnt[dj] += v;
            }
        }
        if (mask != (1 << 10) - 2) {  // (1<<10)-1：1111111111（10个1）而mask没有或上1<<0所以再-1
            return false;
        }

        int cnt = rowCnt[0];
        for (int d = 0; d < 3; d++) {
            if (rowCnt[d] != cnt || colCnt[d] != cnt) {
                return false;
            }
        }
        if (grid[i][j] + grid[i - 1][j - 1] + grid[i - 2][j - 2] != cnt) {
            return false;
        }
        if (grid[i - 2][j] + grid[i - 1][j - 1] + grid[i][j - 2] != cnt) {
            return false;
        }
        return true;
    }
public:
    int numMagicSquaresInside(vector<vector<int>>& grid) {
        int ans = 0;
        int n = grid.size(), m = grid[0].size();
        for (int i = 2; i < n; i++) {
            for (int j = 2; j < m; j++) {
                ans += is(grid, i, j);
            }
        }
        return ans;
    }
};

Python

python 复制代码

'''
LastEditTime: 2025-12-30 13:38:58
'''
from typing import List

class Solution:
    def ok(self, grid: List[List[int]], i: int, j: int) -> bool:
        mask = 0
        colCnt = [0] * 3
        rowCnt = [0] * 3
        for di in range(3):
            for dj in range(3):
                v = grid[i - di][j - dj]
                mask |= 1 << v
                rowCnt[di] += v
                colCnt[dj] += v
        if mask != (1 << 10) - 2:
            return False
        cnt = grid[i][j] + grid[i - 1][j - 1] + grid[i - 2][j - 2]
        if grid[i - 2][j] + grid[i - 1][j - 1] + grid[i][j - 2] != cnt:
            return False
        if any(c != cnt for c in colCnt):
            return False
        if any(r != cnt for r in rowCnt):
            return False
        return True
    
    def numMagicSquaresInside(self, grid: List[List[int]]) -> int:
        return sum(self.ok(grid, i, j) for j in range(2, len(grid[0])) for i in range(2, len(grid)))

同步发文于CSDN和我的个人博客，原创不易，转载经作者同意后请附上原文链接哦~

千篇源码题解已开源