一般来说,数据对的质量很大程度上决定了模型的效果。但干净的数据获得总是很困难的,所以有一些聪明人想出来了一些不需要干净数据的奇思妙想。这里就简单学习一下。
Noise2Noise
Learning image restoration without clean data.ICML 2018,来自英伟达实验室NVlabs
https://github.com/NVlabs/noise2noise
生活中的测量,最常用的就是多次测量求平均值。这背后实际上是最小化测量值y与真实值z之间的损失函数:
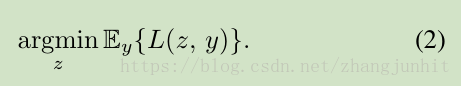
当损失函数L是均方误差时,估计的z就是算术平均值,当损失函数L是绝对误差时,估计的z就是测量值的中位数(median of the observations)。这也可以解释L2损失会考虑更多可能性,把所有点往均值的方向拉,而L1损失可以允许有离群点的出现。
深度学习网络其实也是一样的道理,只不过建模比算术平均复杂一点,使用的是关于的函数f,计算每一对input-target pairs中x经过f映射后与y的误差:
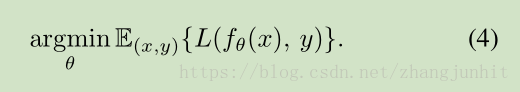
虽然训练数据是一一对应的,但其实暗合的是多对一的关系。以超分辨率任务为例,多个HR经过退化都可能退化到同一个LR,所以在搜索空间中,LR可以有多个候选项。如果是L2损失,那么网络就倾向于选择多个候选项的平均值作为输出。
进一步,如果把target使用zero-mean noise干扰,那么网络的更新情况和以target做ground truth的情况是一样的。因为此时的x和y是同一信号的不同次观测,相对于同一信号叠加了独立同分布的两次噪声,所以f的映射:
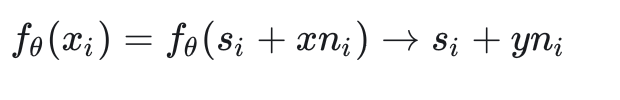
而实际上使用L2 loss时f不会也无法学习到特定的噪声采样,所以只能是估计期望,而这正是我们想要的:

所以只要我们拥有独立同分布的同一内容的数据,就无需显式地定义 p(带噪图像|干净图像) 或 p(干净图像)。
那么需要多少个场景,每个场景需要多少个noisy img呢,论文中做了实验,
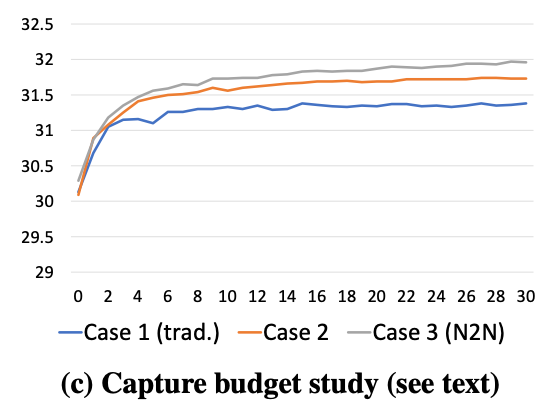
case1是传统的监督学习,场景N=100,每个clean img需要19个noisy imga叠加,叠加后与剩下的那个noisy img构成训练对,所以一共需要2000个noisy img。同样是100个场景,每个场景的noisy img可以有20*19种组合,组合后送入N2N学习,这就是Case2,可以看到效果有提升。仍然保持2000个"capture unit" (CU),拆成1000个场景,每个场景2个noisy imga,这就是case3,可以看到效果在case2的基础上还有提升。
对于高斯噪声,Poisson和Bernoulli都取得了很好的效果。但是对于Random-valued impulse noise,每个像素以一定概率变成随机一种颜色,此时L1和L2得到的结果都偏灰,所以文章提出了L0 loss:
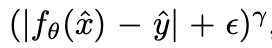
指数部分在训练阶段会线性从2退化到0.
在Monte Carlo Rendering,噪声更加复杂。因为长尾分布,L2不可用,因为HDR的存在,让去噪网络输出Tone mapping之后的结果也有的问题,所以先是引入了类似于relative MSE的
:
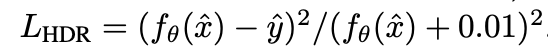
并且对input做tone mapping,而输出仍然维持线性的效果会更好:

假设图像是independent的,并且是零均值zero-mean的。取同一场景的不同图像作为训练网络的input和target。
Under the assumption that noise in each image is independent and has a zero-mean distribution, Noise2Noise [30] takes different images of a scene that act as input and target images for training a network, respectively.
Neighbor2Neighbor
人大和大连理工,CVPR2021https://github.com/TaoHuang2018/Neighbor2Neighbor
虽然N2N使得没有干净图像的训练成为可能,但是要获取同一场景的两次不同观测还是很困难的,比如医学图像,器官是会蠕动的,并且两次观测的光照也会有不同。
所以这篇论文把两次观测的限制进一步放宽:
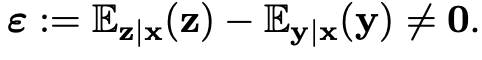
z和y是关于x的两次观测。因为不等于0,所以此时如果仍然使用L2最小化y与z,无法取得和监督训练一样的效果,此时下面两个优化结果是不同的:
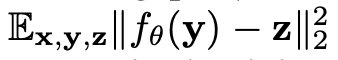
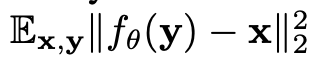
如果还是用noise2noise的方式,就会导致过于平滑。但只要足够小,也可以认为近似相等。
所以需要考虑两个patch之间的差异。网络对g1的输出和g2的差异同时包含了内容的差异和噪声的差异,所以进一步对y过网络后再采样得到的结果做差,减去这部分差异。下面式子描述的是带噪声的patch的差异减去干净图像内容之间的差异:
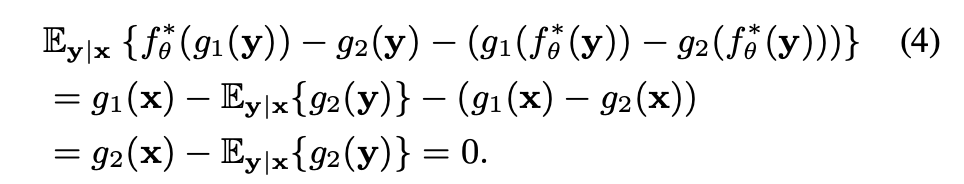
g1和g2是两次观测,如果偏差等于0,那就会退化成noise2noise;如果不等于0,那么按照上面的推导,f是理想去噪时,可以得到上式等于0. 所以neighbor2neighbor可以看作是noise2noise的泛化,同时 可以也考虑了采样带来的差异,而整个公式4等于0约束了f是理想去噪。
从同一个噪声图中随机subsampling得到input-traget。
random neighbor sub-samplers
其实就是在2x2的区域内,随机挑选一个点分别作为g1和g2的结果:
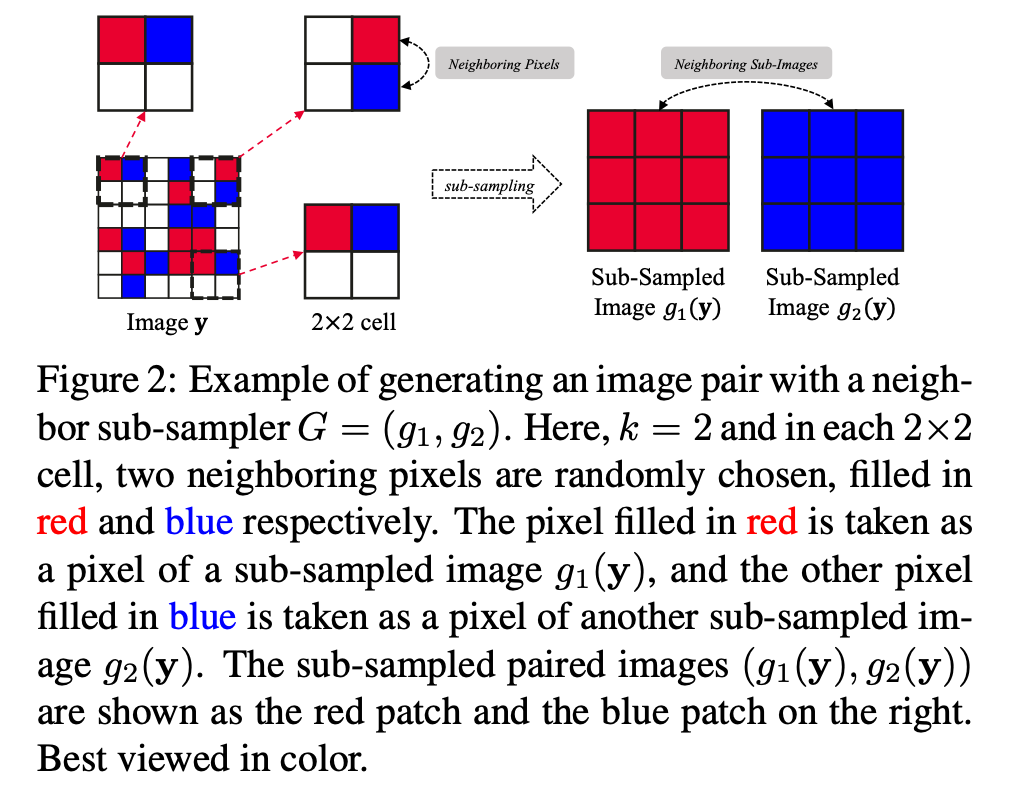
但就是这样简单的操作就满足了两个重要假设:相似性和独立性。
loss
loss分为两部分,第一部分和noise2noise是一样的。网络对g1的输出去拟合g2. 第二部分是约束,就是上面讨论的再减去两个patch的图像真实内容的差异。
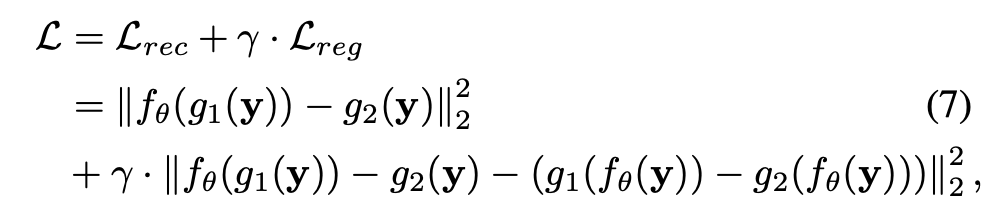
正则项的权重因子取0时,降噪结果会损失细节,过于平滑,而太大时会有很多的噪声残留:

所以γ = 2 for synthetic experiments, and γ = 1for real-world experiments
论文也对比了采样策略的影响:
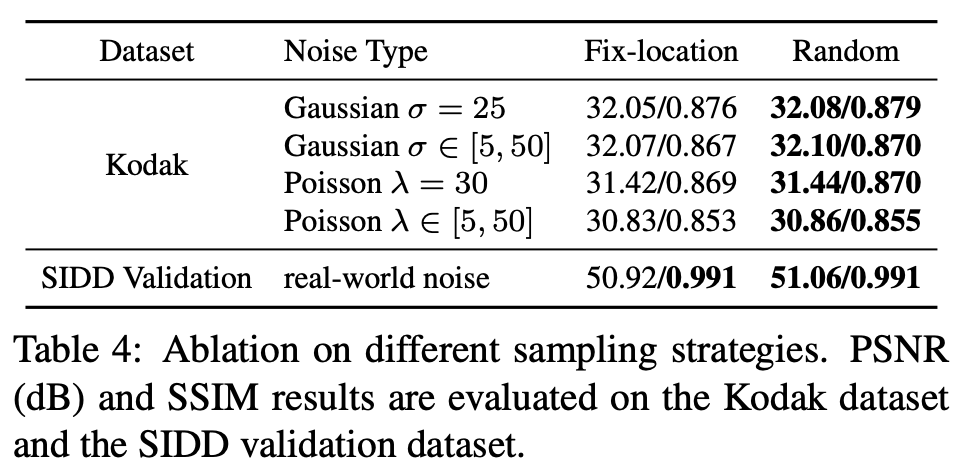
fix-location是所有cell共用相同的随机结果,而论文所提出的方法随机性更强,最终表现也更好。
ZS-N2N
Zero-Shot Noise2Noise,来自CVPR2023,慕尼黑工业大学TUM。基于N2N和Nbr2Nbr,更换了采样策略:通过计算对角线像素的均值构建input-target
Zero-Shot Noise2Noise [35] is another self-supervised learning approach that generates input-target pairs by applying a filter that computes the mean of diag-
onal pixels.
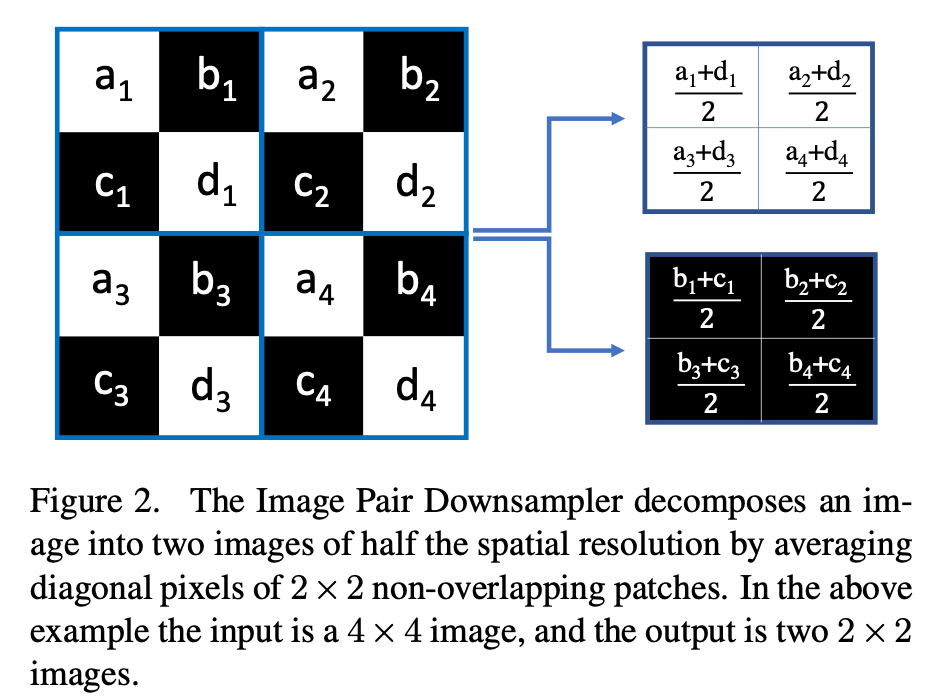
实现上,可以构造stride=2的卷积得到对角线/反对对角线的平均值:
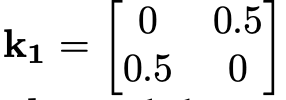
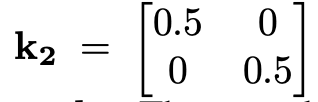
对应代码:
def pair_downsampler(img):
# img has shape B C H W
c = img.shape[1]
filter1 = torch.FloatTensor([[[[0, 0.5], [0.5, 0]]]]).to(img.device) # 形状 [1,1,2,2]
filter1 = filter1.repeat(c, 1, 1, 1)
filter2 = torch.FloatTensor([[[[0.5, 0], [0, 0.5]]]]).to(img.device) # 形状 [1,1,2,2]
filter2 = filter2.repeat(c, 1, 1, 1)
output1 = torch.nn.functional.conv2d(img, filter1, stride=2, groups=c)
output2 = torch.nn.functional.conv2d(img, filter2, stride=2, groups=c) # groups=c:深度卷积模式,每个输入通道独立与对应滤波器卷积
return output1, output2看到这里只是对NB2NB做了采样策略的优化。其实除了采样策略,还有loss的设计和网络的极致简化。它使用的网络让人惊讶,网络只有两个layer,参数量只有20k(一般小的模型是1M)。Self2Self and DIP在内的很多算法使用的还是u-net,参数量很大。ZS-N2N就跳出了U-net的框架,虽然只有两层,但相比于Noise2Fast,ZS-N2N在下采样时没有dropping pixel,所以没有丢失信息。在泛化性,降噪质量,计算量之间取得了很好的平衡。
至于loss,既然是自监督,输入输出端都是带噪声的,那么自然而然可以想到双向一致性计算loss,级交换输入和输出,求均值。同时把网络的拟合目标改为噪声而不是另外一张噪声图。这样重建loss:
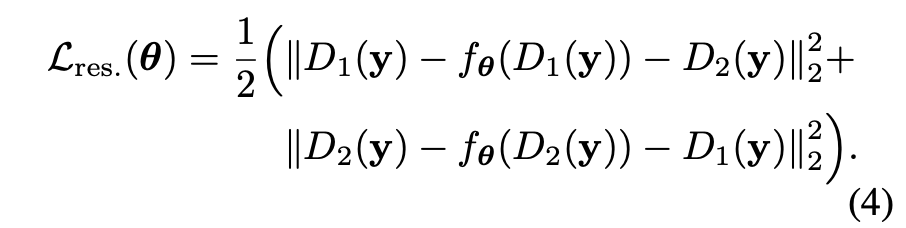
noisy1, noisy2 = pair_downsampler(self.noisy_img)
pred1 = noisy1 - self.cur_model(noisy1)
pred2 = noisy2 - self.cur_model(noisy2)
loss_res = 1 / 2 * (mse(noisy1, pred2) + mse(noisy2, pred1))因为有下采样的策略,网络没有看到全局信息,所以还有一个正则项:去噪后再采样结果和采样后去噪点结果要保持一致性,所以得到:
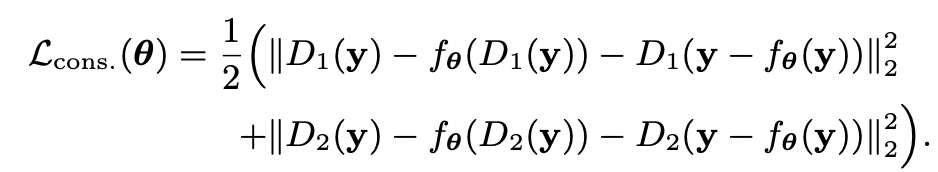
noisy_denoised = self.noisy_img - self.cur_model(self.noisy_img)
denoised1, denoised2 = pair_downsampler(noisy_denoised)
loss_cons = 1 / 2 * (mse(pred1, denoised1) + mse(pred2, denoised2))test-time adaptation (TTA)
Noise2Self
对噪声图像进行固定间隔的掩码,被保留的像素作为输入,被mask掉的作为traget。
Noise2Self [6] is another self-supervised learning method that masks the noisy image at regular intervals, using the remaining pixels as an input image and masked pixels as a target image.
noise2void
来自CVPR2019https://zhuanlan.zhihu.com/p/1895564651913261638
https://github.com/juglab/n2v?tab=readme-ov-file
neighbor2neighbor的思想和noise2noise一样,还是构造两个内容尽可能接近但噪声独立同分布的patch,N2V的做法是直接通过邻域像素去学习中心点。N2V这么做的出发点是认为CNN是noisy img向clean img的映射,但从单个的像素角度来看,其实是把感受野的区域映射到中心的clean pixel。RF表示感受野,那么对单个像素对估计可以写成:
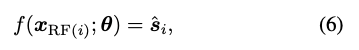
每个像素位置都由信号和噪声构成:
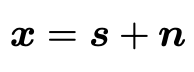
相邻像素位置的信号之间是相关的:
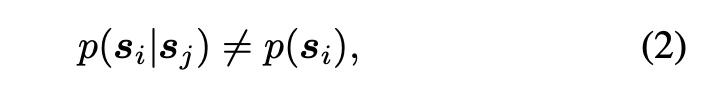
而在给定信号之后,噪声之间可以看作是独立的:
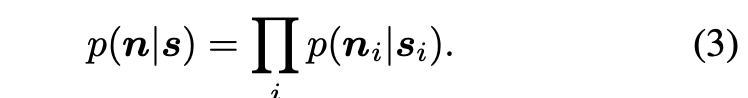
所以N2V的优化目标就是由周围像素去拟合中心像素,相当于噪声和信号项分别去拟合中心值,这样最终得到的也会是干净的中心像素。
但如果仍然像传统的监督学习一样,直接把输入和target都换成同一个带噪声的图,那么就会学到恒等映射。为了避免恒等映射,故意把感受野的中心点去除,这就是盲点(blind-spot)网络:
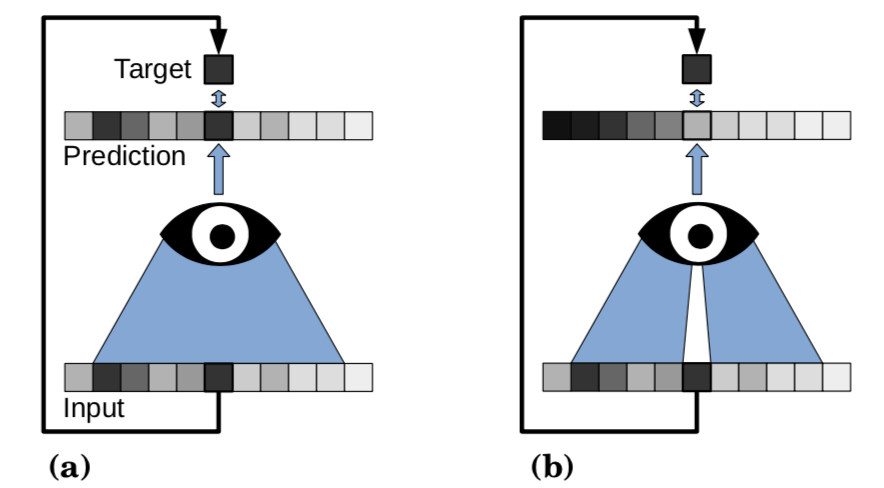
具体实现上,首先是切成64x64大小的patch,再使用stratified sampling采样得到N个点,同时使用mask记录这些点的位置。对这些点再随机使用它们的邻域的点替换,拟合目标就是依据于mask只拟合替换前的值。
Noise2Void通过随机遮蔽(masking)图像中的部分像素,并训练模型预测这些被遮蔽像素的真实值,从而实现自监督学习。掩模比例直接影响:
- 训练效率:比例过高会导致有效信息减少,模型难以收敛;比例过低则可能无法充分学习噪声分布。
- 去噪效果:适当比例能平衡噪声去除与细节保留,避免过度平滑或伪影。
随机改变点的比例(即掩模比例)通常设置为5%至10%,这一范围在图像去噪任务中表现稳定且效果较好。
因为N2V主动舍弃了中心像素的信息,所以当信号不是那么规则时(比如有一个孤立的点,或者全局都分布很不规则),容易预测出错:
 如果噪声分布不满足均值等于0(如有固定模式噪声),那么噪声也会残留:
如果噪声分布不满足均值等于0(如有固定模式噪声),那么噪声也会残留:

Self2Self
集成学习,很慢,丢失细节。
1.https://zhuanlan.zhihu.com/p/683401621