逻辑回归-泰坦尼克号

逻辑回归

一、逻辑回归概念

逻辑回归是深度学习中最基础的分类算法之一，虽然名字里有 "回归"，但它本质上解决的是二分类问题（比如判断 "是垃圾邮件" 或 "不是"、"图像是猫" 或 "不是"）。

它的核心思想可以概括为：

先用线性函数对输入数据进行加权求和，得到一个 "分数"；
再通过一个函数将这个分数转换为 0 到 1 之间的概率值，代表属于某一类的可能性；
最后根据概率值设定阈值（通常是 0.5），决定分类结果。

1.1 Sigmoid

Sigmoid函数表达式为：

f(x)=11+e−xf(x) = \frac{1}{1 + e^{-x}}f(x)=1+e−x1

Sigmoid函数的取值范围为(0, 1)，适用于二分类问题。Sigmoid函数将输入映射到一个"概率"范围，使得较小的输入靠近 0，较大的输入接近 1。

得到概率后，设定阈值（如0.5）：

若 σ(z)≥0.5\sigma(z) \geq 0.5σ(z)≥0.5，预测为正类（标签 y=1y=1y=1）；
若 σ(z)<0.5\sigma(z) < 0.5σ(z)<0.5，预测为负类（标签 y=0y=0y=0）。

1.2损失函数-交叉熵损失（Cross-Entropy Loss）

所以我们不妨将线性回归模型带入到Sigmoid函数中来看，这样就有了一个新的二分类预测模型

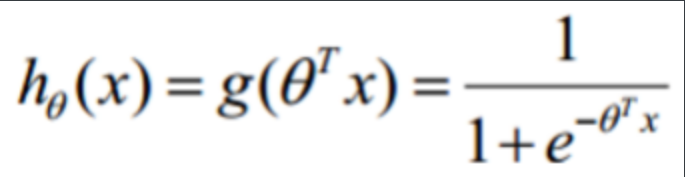
g(z)的取值是0到1之间，我们可以把它的值看成是概率，即

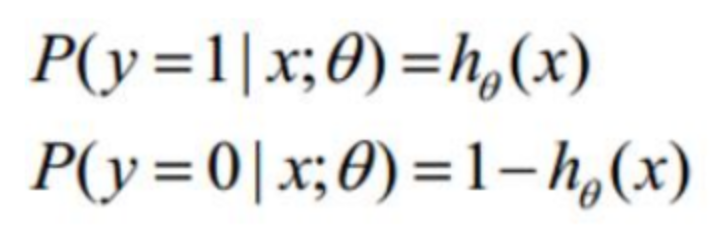
整合：

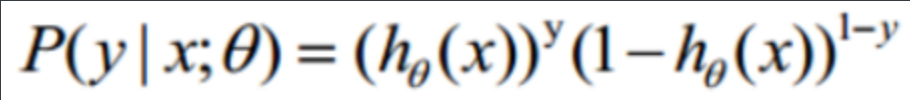
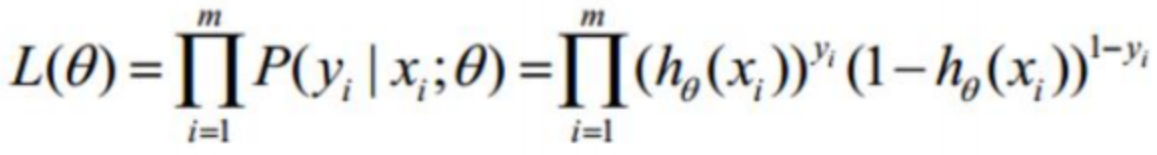
这个公式就叫似然函数，用它的值来表示θ所构建的这个模型与数据真实模型的相似程度

因为乘法并不便于我们后期的计算，所以我们想个办法将它变成加法，于是两边同时取对数通过对数变换可以完美解决这两个问题，核心数学原理是：
log(a⋅b⋅c)=log(a)+log(b)+log(c)log(a⋅b⋅c)=log(a)+log(b)+log(c)log(a⋅b⋅c)=log(a)+log(b)+log(c)

对上述似然函数两边取自然对数：log⁡L(θ∣x1,x2,...,xN)=log⁡(∏i=1NP(xi∣θ))=∑i=1Nlog⁡P(xi∣θ)\log L(\theta | x_1, x_2, \dots, x_N) = \log \left( \prod_{i=1}^N P(x_i | \theta) \right) = \sum_{i=1}^N \log P(x_i | \theta)logL(θ∣x1,x2,...,xN)=log(∏i=1NP(xi∣θ))=∑i=1NlogP(xi∣θ)

这样，我们将似然的连乘 转换为对数似然的累加，简化了计算。

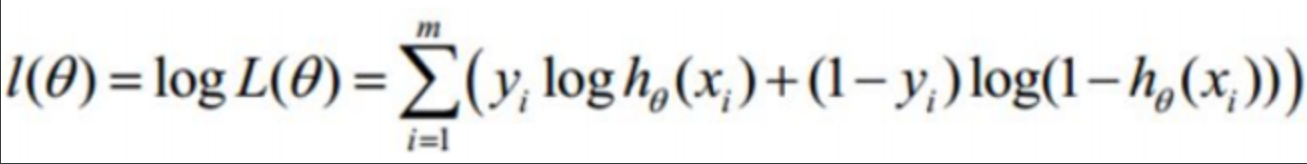
这个公式就叫对数似然函数

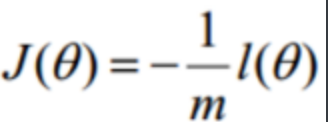
逻辑回归使用交叉熵损失来衡量预测概率与真实标签的差异。对于单个样本，真实标签 yyy（0或1），预测概率 y^=σ(z)\hat{y} = \sigma(z)y^=σ(z)，损失函数为：

L(y^,y)=−[ylog⁡y^+(1−y)log⁡(1−y^)]L(\hat{y}, y) = -[y \log\hat{y} + (1-y)\log(1-\hat{y})]L(y^,y)=−[ylogy^+(1−y)log(1−y^)]

二、泰坦尼克号数据清理

我们首先, 加载泰坦尼克号的训练数据集:

python 复制代码

import pandas as pd

train_data = pd.read_csv(r'./titanic/train.csv')
train_data

运行结果:

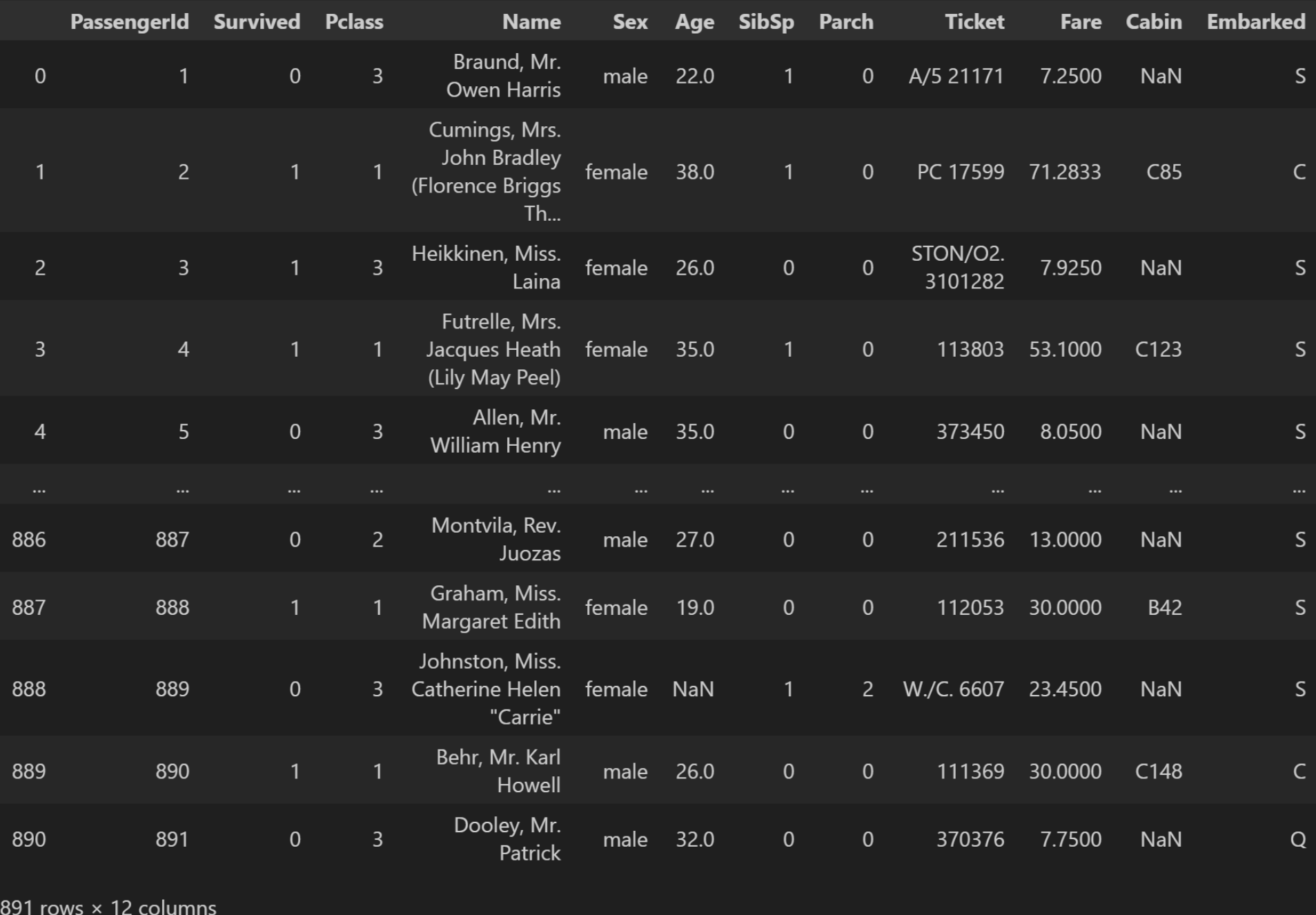
同时也把测试数据集加载进来:

python 复制代码

test_data = pd.read_csv(r'./titanic/test.csv')
test_data

结果:

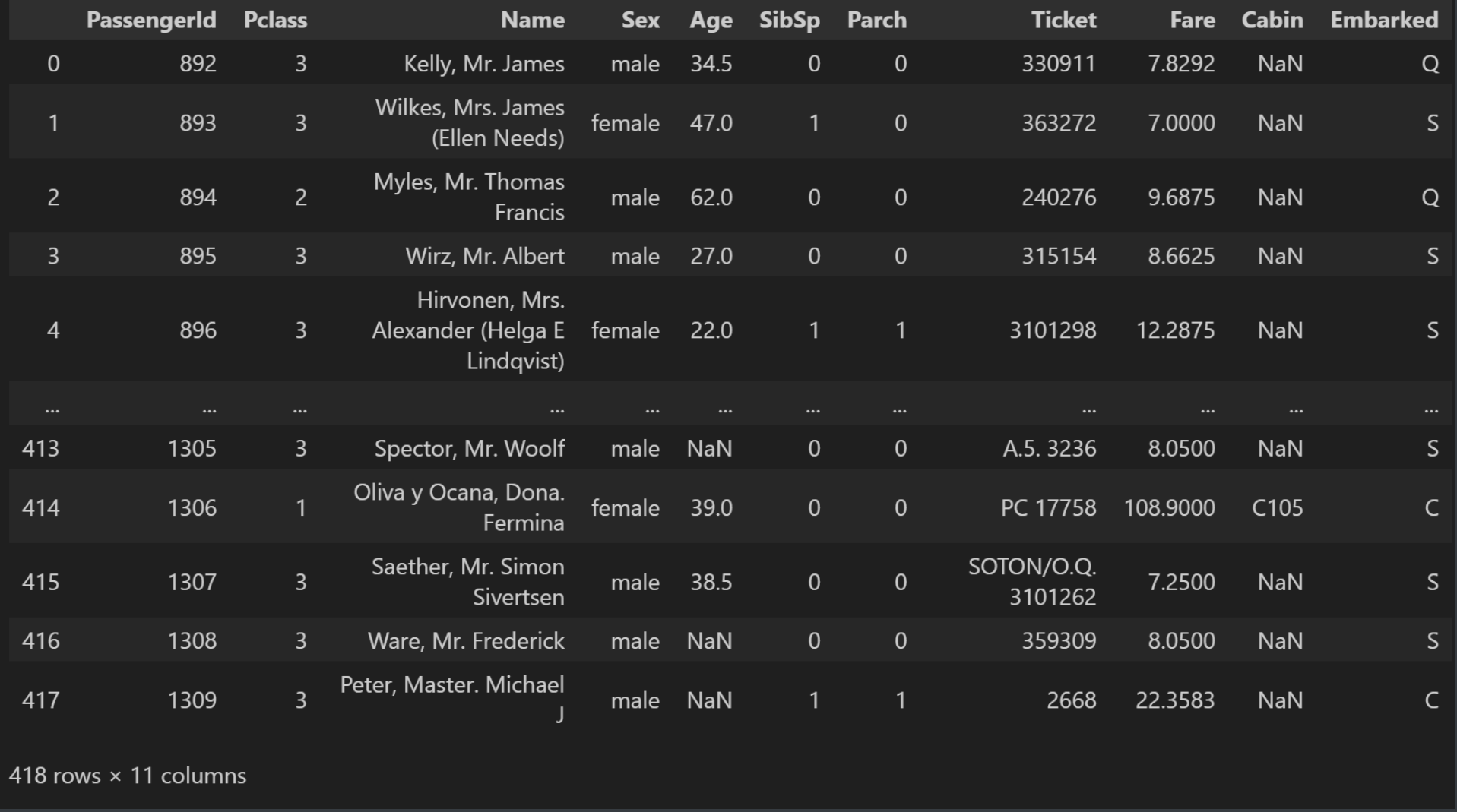
我们把训练集和测试集合并起来, 合并的时候不需要排序:

python 复制代码

full_data = pd.concat([train_data, test_data], sort=False)
full_data

合并之后的数据:

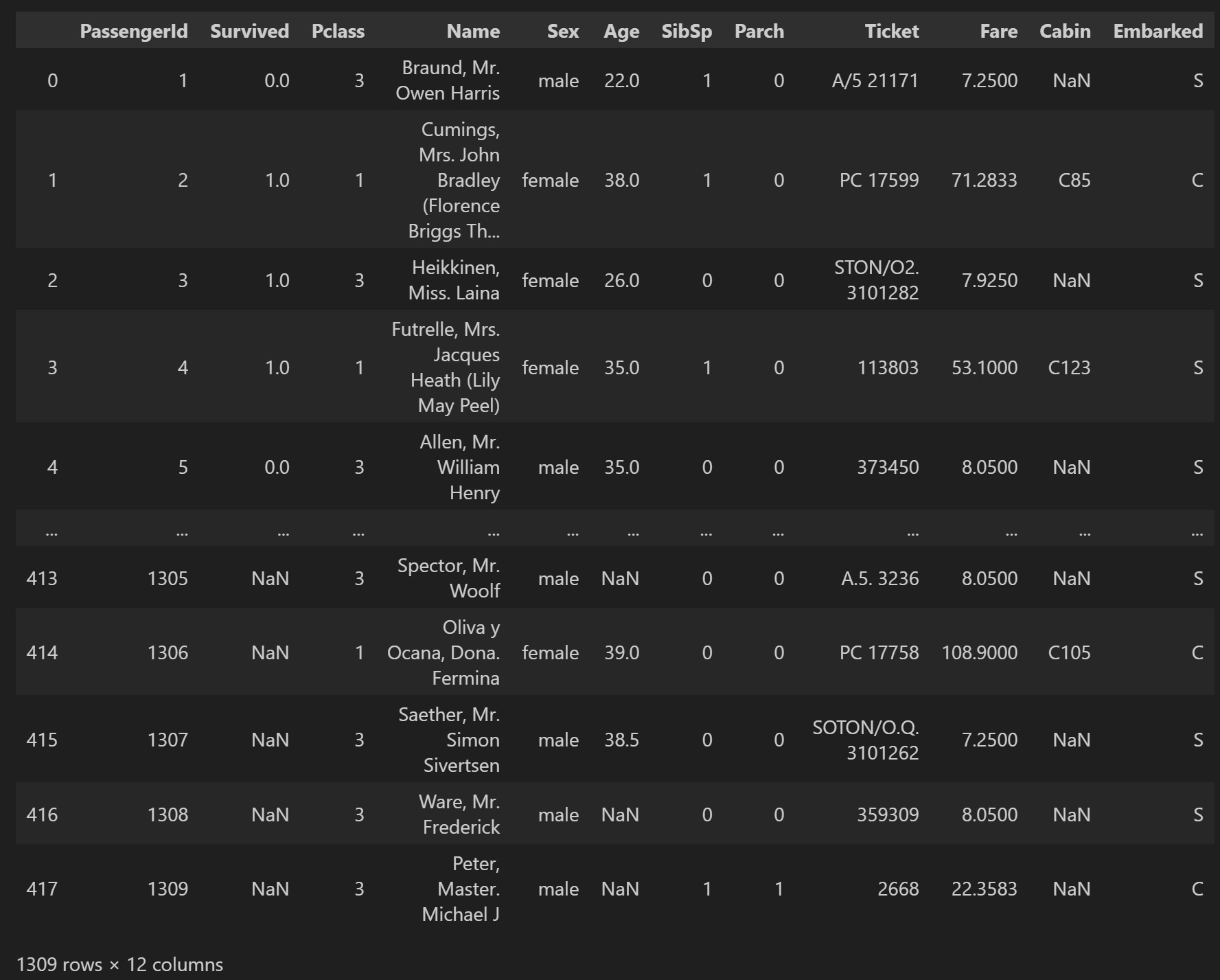
查看合并后的数据基本信息:

python 复制代码

full_data.info()

结果:

text 复制代码

<class 'pandas.core.frame.DataFrame'>
Index: 1309 entries, 0 to 417
Data columns (total 12 columns):
 #   Column       Non-Null Count  Dtype  
---  ------       --------------  -----  
 0   PassengerId  1309 non-null   int64  
 1   Survived     891 non-null    float64
 2   Pclass       1309 non-null   int64  
 3   Name         1309 non-null   object 
 4   Sex          1309 non-null   object 
 5   Age          1046 non-null   float64
 6   SibSp        1309 non-null   int64  
 7   Parch        1309 non-null   int64  
 8   Ticket       1309 non-null   object 
 9   Fare         1308 non-null   float64
 10  Cabin        295 non-null    object 
 11  Embarked     1307 non-null   object 
dtypes: float64(3), int64(4), object(5)
memory usage: 132.9+ KB

我们把那些数值类型的属性全部提取出来:

python 复制代码

# 记录数值类型的列
numeric_cols = ns
numeric_colsfull_data.select_dtypes(include=['number']).columns

结果:

text 复制代码

Index(['PassengerId', 'Survived', 'Pclass', 'Age', 'SibSp', 'Parch', 'Fare'], dtype='object')

在这些数值类型的属性中, 我们把生存的属性当作标签, 把其它属性当作特征:

python 复制代码

# 标签
label_cols = ['Survived']
# 特征
numeric_cols = ['Pclass', 'Age', 'SibSp', 'Parch', 'Fare']

我们对数值类型的那5个属性, 进行均值填充处理:

python 复制代码

for col in numeric_cols:
    full_data[col] = full_data[col].fillna(full_data[col].mean())

接下来我们对数值类型的那5个属性数据部分进行标准化处理:

python 复制代码

from sklearn.preprocessing import StandardScaler

X_strandard = StandardScaler()

# 单独给原来的数值列进行标准化
X_strandard_data = pd.DataFrame(X_strandard.fit_transform(
    full_data[numeric_cols]),
                                columns=numeric_cols)
X_strandard_data

标准化后的运行结果:

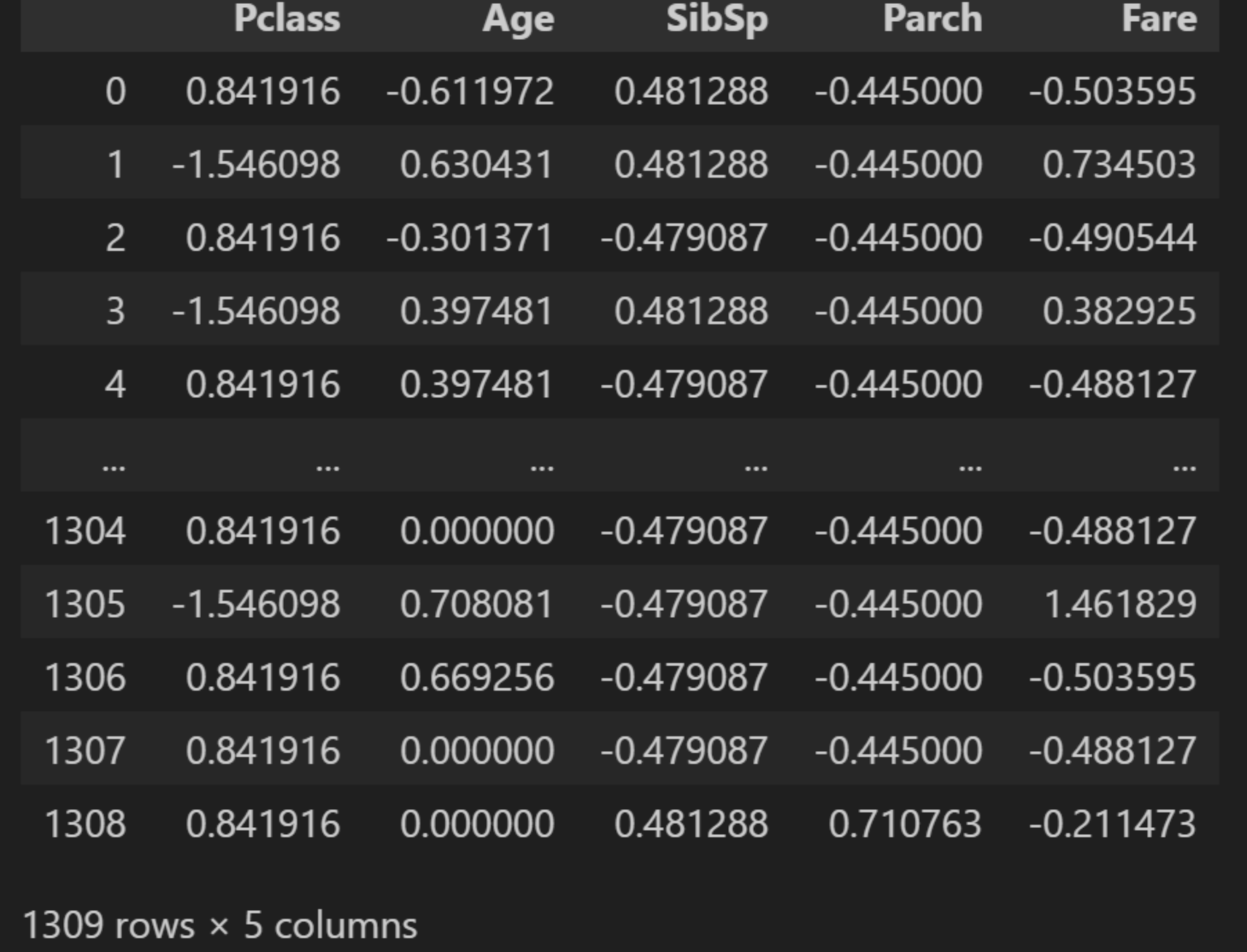
接下来我们对人名取出姓氏:

python 复制代码

full_data['Title'] = full_data['Name'].str.extract(r'([A-Za-z]+)\.',
                                                   expand=False)  # Mr.
full_data

结果:

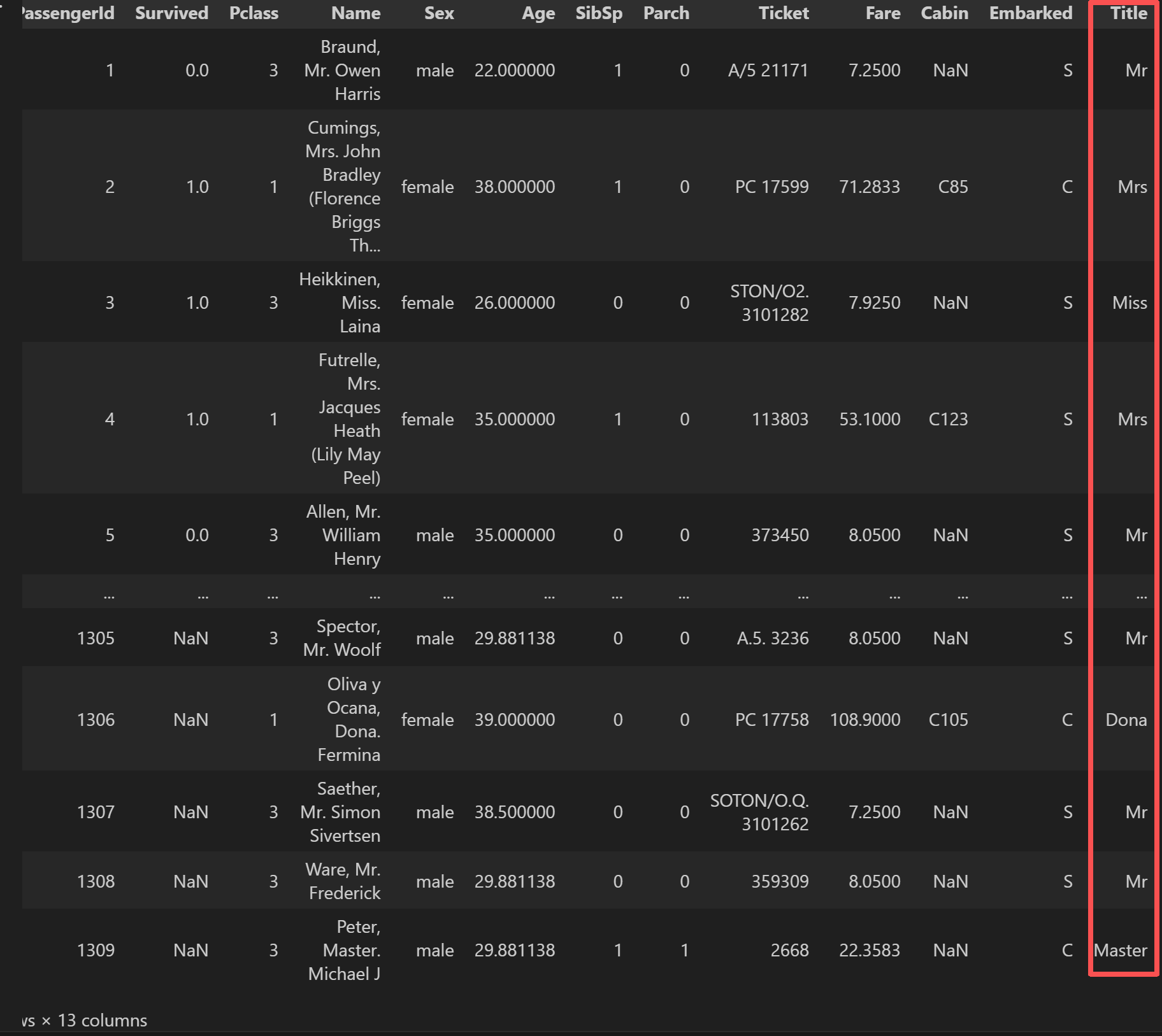
我们把剩下那些没有选的属性也都展示出来:

python 复制代码

other_cols = full_data.columns.difference(numeric_cols)
other_cols

结果:

text 复制代码

Index(['Cabin', 'Embarked', 'Name', 'PassengerId', 'Sex', 'Survived', 'Ticket',
       'Title'],
      dtype='object')

我们在这里面取期中三个属性:

python 复制代码

other_cols = ['Sex', 'Embarked', 'Title']

我们一样对取出来的这三个属性, 进行填充, 以众数的方法填充:

python 复制代码

for col in other_cols:
    full_data[col] = full_data[col].fillna(full_data[col].mode()[0])

随后我们对这三个属性进行独热编码:

python 复制代码

other_cols_data = pd.get_dummies(full_data[other_cols], dtype=int)
other_cols_data

结果:

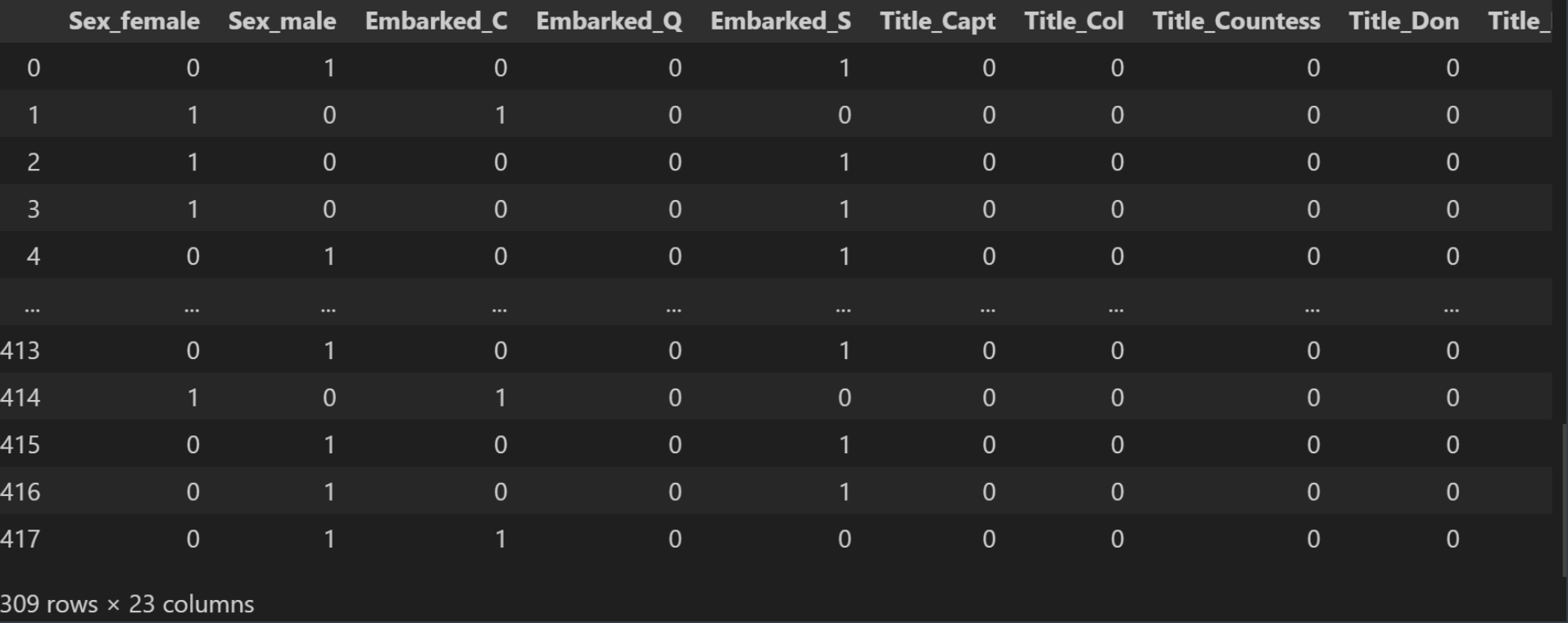
上一篇文章(权重衰减, 文章链接: https://blog.csdn.net/m0_55297736/article/details/156085739?spm=1011.2124.3001.6209)详细讲了讲独热编码的实现原理, 里面有包含底层实现的代码, 那么这边就不再赘述, 我们可以直接使用pandas里面内置的函数, 叫做get_dummies, 这个函数就是用来做独热编码用的。

获取标签列里面的数据:

python 复制代码

# 标签列
Y_strandard_data = pd.DataFrame(full_data[label_cols], columns=label_cols)
Y_strandard_data

结果:

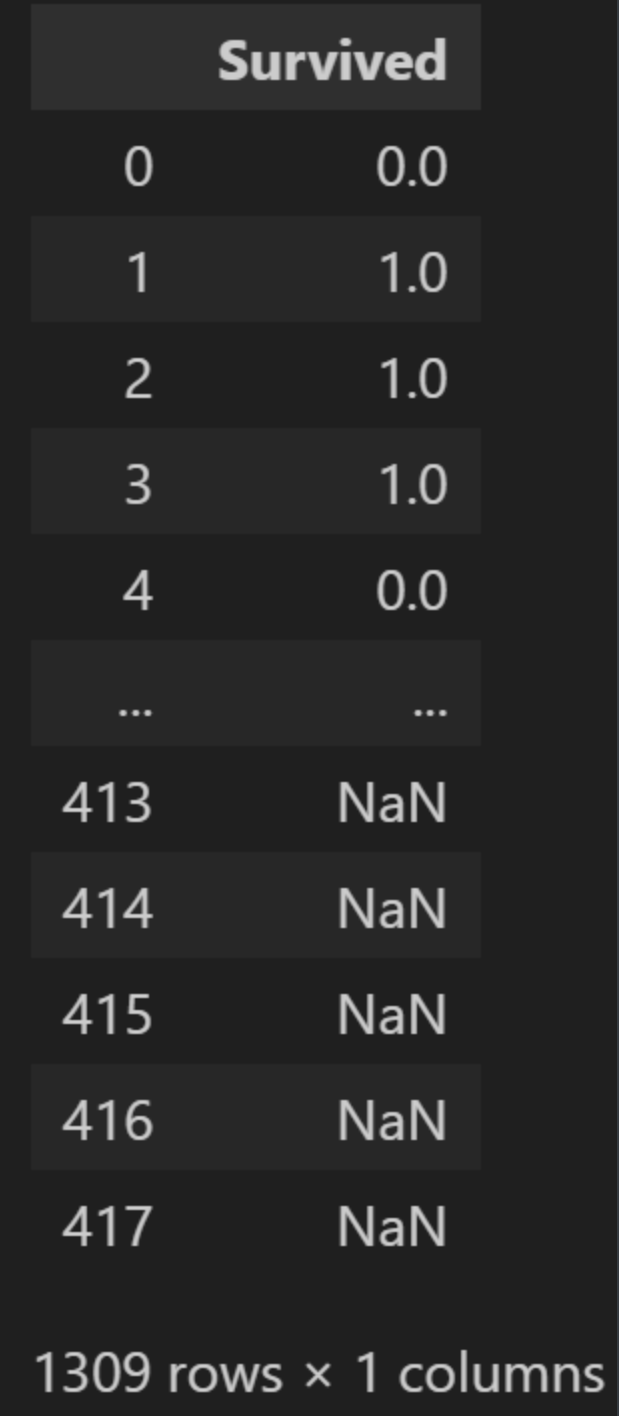
我们接下来将标准化过后的特征跟独热编码的数据还有标准化过后的标签进行合并:

python 复制代码

X_strandard_data = X_strandard_data.reset_index(drop=True)
other_cols_data = other_cols_data.reset_index(drop=True)
Y_strandard_data = Y_strandard_data.reset_index(drop=True)

# 合并 标准化的数值列和独热编码列和标签列
merged_data = pd.concat([X_strandard_data, other_cols_data, Y_strandard_data],
                        axis=1)
merged_data

结果:

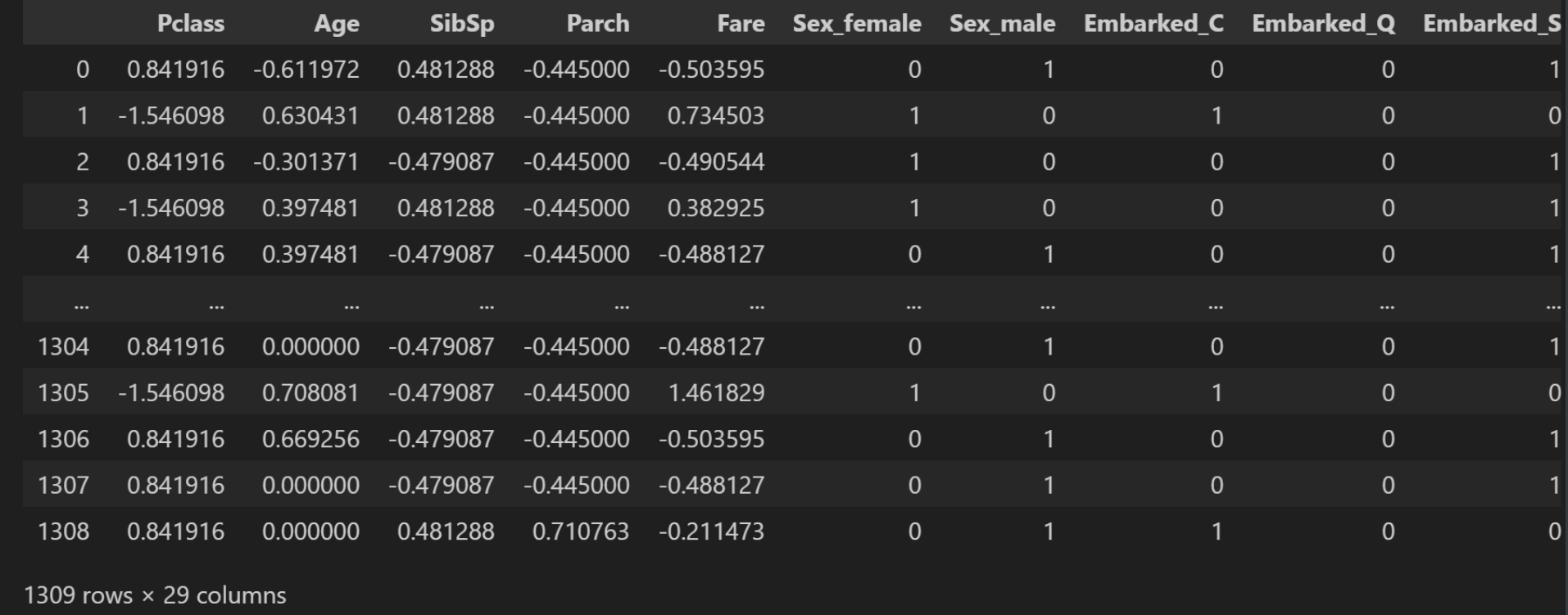
我们可以看到里面有29列数据。

最后我们将数据保存到csv文件里面去:

python 复制代码

merged_data.to_csv('data.csv', index=False)

三、构建模型并预测结果

首先, 我们还是一样, 得先"固定随机性"，目的是让实验可复现:

python 复制代码

import numpy as np
import torch


def seed_everything(seed=42):
    np.random.seed(seed)
    torch.manual_seed(seed)
    torch.cuda.manual_seed(seed)
    torch.cuda.manual_seed_all(seed)
    torch.backends.cudnn.deterministic = True
    torch.backends.cudnn.benchmark = False


seed_everything()

我们导入刚才已经准备好的数据:

python 复制代码

import pandas as pd

data = pd.read_csv('data.csv')
data

结果:

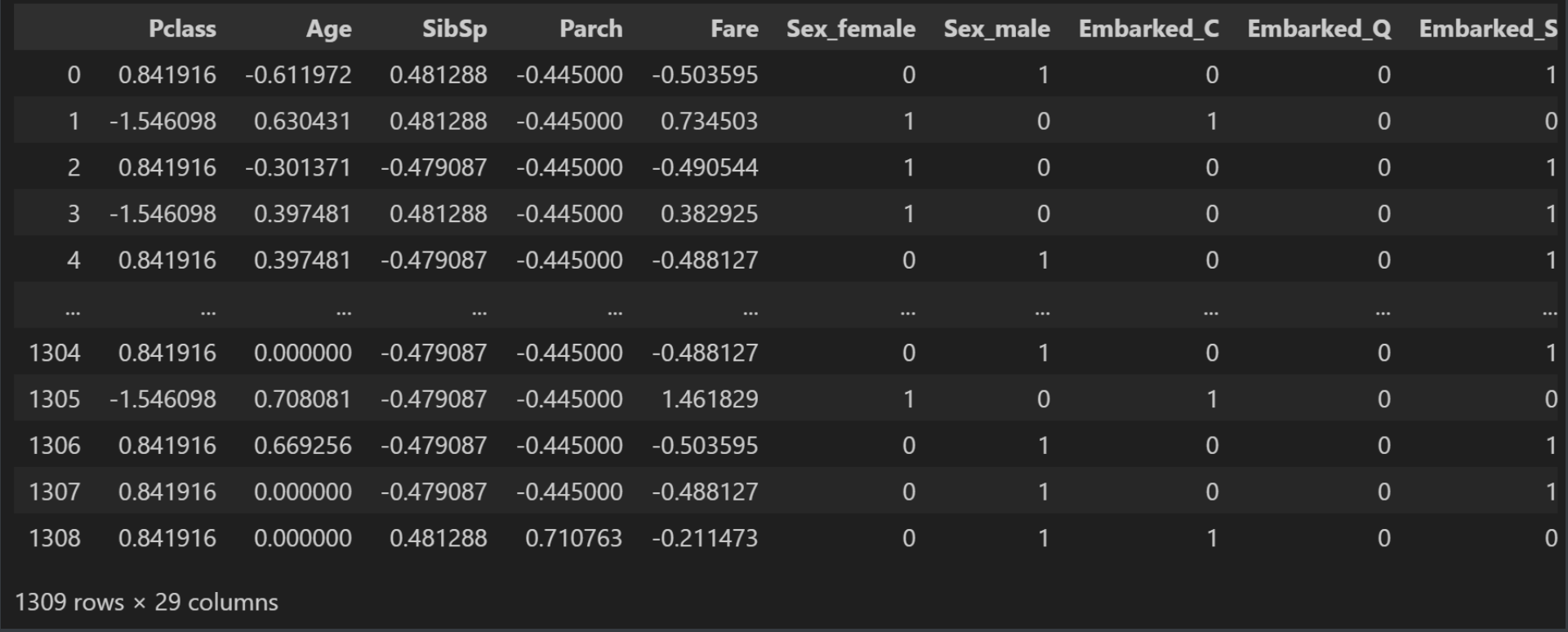
我们看一下训练集数据:

python 复制代码

train_data = data[:891]
train_data

训练集数据:

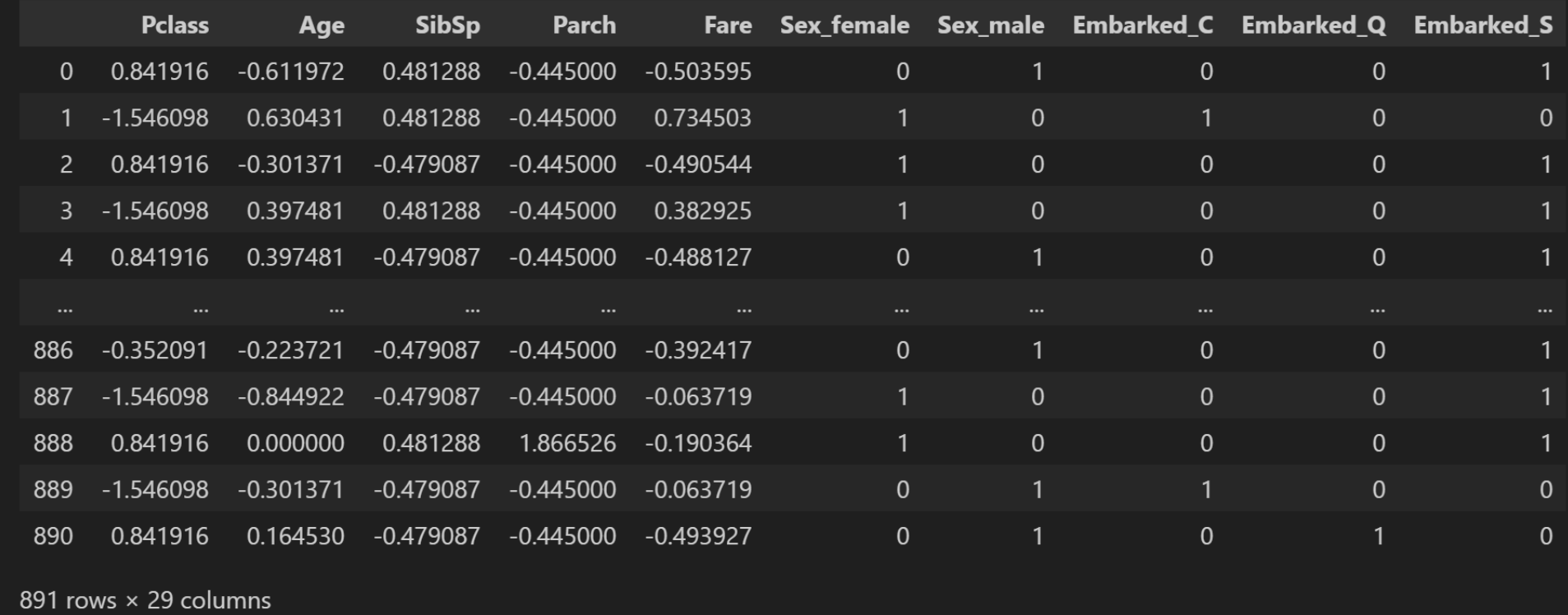
获取特征和标签:

python 复制代码

# 特征和标签
X_strandard_data = train_data.drop('Survived',
                                   axis=1)  # 对dataframe做删除-dataframe
Y_strandard_data = train_data['Survived']  # 去dataframe的一列-series
X_strandard_data

我们需要用GPU跑模型, 实在没有GPU就使用CPU:

python 复制代码

import torch

device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
device

运行结果:

text 复制代码

device(type='cuda')

特征和标签的形状:

python 复制代码

X_tensor = torch.tensor(X_strandard_data.values).to(device)
y_tensor = torch.tensor(Y_strandard_data.values).view(-1, 1).to(device)
X_tensor.shape, y_tensor.shape

结果:

text 复制代码

(torch.Size([891, 28]), torch.Size([891, 1]))

接下来我们构建泰坦尼克号模型:

python 复制代码

from torch import nn


class TitanicModel(nn.Module):

    def __init__(self, input_size) -> None:
        super().__init__()
        self.linear1 = nn.Linear(input_size, 64)
        self.linear2 = nn.Linear(64, 32)
        self.linear3 = nn.Linear(32, 16)
        self.linear4 = nn.Linear(16, 8)
        self.output = nn.Linear(8, 1)
        self.relu = nn.ReLU()
        self.droupt = nn.Dropout(0.2)  # p=0.2 丢弃20%的神经元信息

    def forward(self, x):
        x = self.relu(self.linear1(x))
        x = self.droupt(x)

        x = self.relu(self.linear2(x))
        x = self.droupt(x)

        x = self.relu(self.linear3(x))
        x = self.droupt(x)

        x = self.relu(self.linear4(x))
        return self.output(x)  # 注意，输出层不需要激活函数

然后我们利用k折交叉验证法, 需要导入KFold:

python 复制代码

from sklearn.model_selection import KFold

k_folds = 5 # 分为5块
kfold = KFold(n_splits=k_folds, shuffle=True) # shuffle值为True意为着完全打乱

接下来我们存储每个折的数据:

python 复制代码

# 存储每个折的结果
fold_results = []
# 记录最好的准确度
best_accuracy = 0.0
# 模型保存地址(目录)
model_dir = 'models'

我们对泰坦尼克号模型进行K折交叉验证训练:

python 复制代码

from torch.utils.data import Subset, DataLoader, TensorDataset
from torch import optim

batch_size = 32
for fold, (train_ds, val_ids) in enumerate(kfold.split(train_data)):
    print(f'Fold {fold+1}/{k_folds}')  # Fold 1/5
    # print(fold, train_ds, val_ids)
    # 构建训练、验证子集
    train_subset = Subset(TensorDataset(X_tensor, y_tensor),
                          train_ds)  # 通过采样得到的样本id，从TensorDataset中获取样本 构成训练子集
    val_subset = Subset(TensorDataset(X_tensor, y_tensor), val_ids)
    # 构建数据加载器
    train_loader = DataLoader(train_subset,
                              batch_size=batch_size,
                              shuffle=True)
    val_loader = DataLoader(val_subset, batch_size=batch_size)
    # 泰坦尼克号模型构建
    model = TitanicModel(X_tensor.shape[1]).to(device)
    criterion = nn.BCEWithLogitsLoss() # 利用交叉熵损失函数
    optimizer = optim.Adam(model.parameters(), lr=0.001, weight_decay=1e-4) # Adam优化器

    # 模型训练
    num_epochs = 1000

    train_losses = []
    test_losses = []

    patience = 100
    best_val_loss = float('inf')
    
    fold_best_model_path = './models/best_housing_model_fold_{}.pth'.format(fold+1)

    for epoch in range(num_epochs):
        model.train()
        epoch_loss = 0 # 每个epoch的损失 每个批次的总损失
        for bacth_X, batch_y in train_loader:
            # 对每个批次进行训练
            y_pred = model(bacth_X)
            loss = criterion(y_pred, batch_y)
            epoch_loss += loss.item()  # 累计损失
            optimizer.zero_grad()
            loss.backward()
            optimizer.step()
        avg_train_loss = epoch_loss / len(train_loader)
        train_losses.append(avg_train_loss)

        # 模型评估
        model.eval()
        with torch.no_grad():
            val_loss = 0
            all_preds = []
            all_labels = []

            for batch_X, batch_y in val_loader:
                y_pred = model(batch_X) # 连续值， 概率分数值
                loss = criterion(y_pred, batch_y)
                val_loss += loss.item()

                preds = (torch.sigmoid(y_pred) >= 0.5).int()  # 二分类阈值0.5
                all_preds.extend(preds.cpu().numpy())
                all_labels.extend(batch_y.cpu().numpy())
            
            avg_val_loss = val_loss / len(val_loader)
            test_losses.append(avg_val_loss)

        accuracy = np.mean(np.array(all_preds) == np.array(all_labels))
        print(f'Fold {fold+1}, Epoch {epoch+1}, Accuracy: {accuracy:.4f}')

        if (epoch+1) % 10 == 0:
            print(
                f'Epoch [{epoch+1}/{num_epochs}], Train Loss: {avg_train_loss:.4f}, Val Loss: {avg_val_loss:.4f}'
            )

        if val_loss < best_val_loss:
            best_val_loss = val_loss
            print(f'best model found at epoch {epoch+1}, Train Loss: {avg_train_loss:.4f}, Val Loss: {avg_val_loss:.4f}')
            torch.save(model.state_dict(), fold_best_model_path)
            best_accuracy = accuracy
            patience = 0
        else:
            patience += 1
            if patience >= 100:
                print("Early stopping triggered")
                break
    fold_results.append({
        'fold': fold + 1,
        'best_val_loss': best_val_loss,
        'best_model_path': fold_best_model_path,
        'train_losses': train_losses,
        'test_losses': test_losses,
        'best_accuracy': best_accuracy
    })

运行结果:

text 复制代码

Fold 1/5
Fold 1, Epoch 1, Accuracy: 0.5866
best model found at epoch 1, Train Loss: 0.6782, Val Loss: 0.6761
Fold 1, Epoch 2, Accuracy: 0.5866
best model found at epoch 2, Train Loss: 0.6635, Val Loss: 0.6419
Fold 1, Epoch 3, Accuracy: 0.7263
best model found at epoch 3, Train Loss: 0.6016, Val Loss: 0.5648
Fold 1, Epoch 4, Accuracy: 0.7933
best model found at epoch 4, Train Loss: 0.5491, Val Loss: 0.5045
Fold 1, Epoch 5, Accuracy: 0.7989
best model found at epoch 5, Train Loss: 0.5011, Val Loss: 0.4698
Fold 1, Epoch 6, Accuracy: 0.8045
best model found at epoch 6, Train Loss: 0.4896, Val Loss: 0.4390
Fold 1, Epoch 7, Accuracy: 0.8101
best model found at epoch 7, Train Loss: 0.4769, Val Loss: 0.4270
Fold 1, Epoch 8, Accuracy: 0.8101
best model found at epoch 8, Train Loss: 0.4555, Val Loss: 0.4154
Fold 1, Epoch 9, Accuracy: 0.8101
best model found at epoch 9, Train Loss: 0.4492, Val Loss: 0.4128
Fold 1, Epoch 10, Accuracy: 0.7989
Epoch [10/1000], Train Loss: 0.4451, Val Loss: 0.4137
Fold 1, Epoch 11, Accuracy: 0.8045
best model found at epoch 11, Train Loss: 0.4205, Val Loss: 0.4095
Fold 1, Epoch 12, Accuracy: 0.8101
Fold 1, Epoch 13, Accuracy: 0.8101
...
Fold 5, Epoch 123, Accuracy: 0.8090
Fold 5, Epoch 124, Accuracy: 0.8146
Fold 5, Epoch 125, Accuracy: 0.8258
Early stopping triggered

我们可以看到每个折训练到后面准确度基本上都稳在80及以上, 由于输出内容不能写太长, 所以很多都省略了。

我们可以看一看平均的准确率和每个折的准确率:

python 复制代码

print("=" * 5, 'K折交叉验证', "=" * 5)
avg_accuracy = np.mean([result['best_accuracy'] for result in fold_results])
print(f"平均准确率: {avg_accuracy:.4f}")
print(f"每个折的准确率")
for result in fold_results:
    print(f"折 {result['fold']}: 准确率: {result['best_accuracy']:.4f}")

运行结果:

text 复制代码

===== K折交叉验证 =====
平均准确率: 0.8306
每个折的准确率
折 1: 准确率: 0.8045
折 2: 准确率: 0.8146
折 3: 准确率: 0.8876
折 4: 准确率: 0.8090
折 5: 准确率: 0.8371

我们可以很清晰的看出每个折的准确率是多少和平均的准确率是多少。

好了, 关于这篇逻辑回归的内容就到此结束了。那关于线性回归的内容, 也就到此结束了, 接下来的文章, 会讲解关于逻辑回归的内容。

以上就是逻辑回归的所有内容了, 如果有哪里不懂的地方,可以把问题打在评论区, 欢迎大家在评论区交流!!!

如果我有写错的地方, 望大家指正, 也可以联系我, 让我们一起努力, 继续不断的进步.

学习是个漫长的过程, 需要我们不断的去学习并掌握消化知识点, 有不懂或概念模糊不理解的情况下,一定要赶紧的解决问题, 否则问题只会越来越多, 漏洞也就越老越大.

人生路漫漫, 白鹭常相伴!!!

逻辑回归-泰坦尼克号

逻辑回归

目录

1.逻辑回归概念

1.1Sigmoid

1.2损失函数-交叉熵损失（Cross-Entropy Loss）

2.泰坦尼克号数据清理

3.构建模型并预测结果

一、逻辑回归概念

1.1 Sigmoid

1.2损失函数-交叉熵损失（Cross-Entropy Loss）

二、泰坦尼克号数据清理

三、构建模型并预测结果