Monostatic Sensing With OFDM Under Phase Noise: From Mitigation to Exploitation

摘要------本文研究了在存在由振荡器不完美引起的相位噪声（PN）的情况下，基于正交频分复用（OFDM）的雷达通信一体化（JRC）系统的单站雷达感知问题。我们首先针对自由运行振荡器（free-running oscillators，FRO）和锁相环（phase-locked loops，PLL），对雷达接收机中跨越多个 OFDM 符号的相位噪声进行了严格的统计特性描述。基于与时延相关的相位噪声协方差矩阵，我们推导了确定性时延-多普勒参数和随机相位噪声的混合最大似然（ML）/最大后验（MAP）估计器，该问题最终转化为一个极具挑战性的高维非线性优化问题（resulting in a challenging high-dimensional nonlinear optimization problem）。

为了规避相位噪声的非线性，我们随后开发了一种迭代小角度近似（iterated small angle approximation，ISAA）算法，该算法在每次迭代中通过将相位噪声作为时延-多普勒的函数进行闭式更新，从而逐步优化时延-多普勒及相位噪声的估计值。此外，现有的方法通常将相位噪声视为必须消除的纯粹损伤，而我们与其不同，提出利用相位噪声来解决距离模糊问题。具体而言，我们通过构建一个参数化 Toeplitz-块 Toeplitz 协方差矩阵重构问题，利用了相位噪声与时延相关的统计特性（即距离相关效应）。

仿真结果表明，在各种工作条件下，无论是针对 FRO 还是 PLL，ISAA 算法都能快速收敛至混合克拉美罗界（CRB），并且相较于现有的最先进基准算法具有显著的性能增益。同时结果也证实，相位噪声的不利影响可以转化为感知的优势。

索引词------OFDM，雷达通信一体化，相位噪声，利用，迭代小角度近似。

文章目录

• • [I. INTRODUCTION](#I. INTRODUCTION)
  • [II. SYSTEM MODEL AND PROBLEM FORMULATION](#II. SYSTEM MODEL AND PROBLEM FORMULATION)
  • • [A. Transmit Signal Model](#A. Transmit Signal Model)
    • [B. Receive Signal Model](#B. Receive Signal Model)
    • [C. Fast-Time/Slow-Time Representation With Phase Noise](#C. Fast-Time/Slow-Time Representation With Phase Noise)
    • [D. 特例：理想振荡器](#D. 特例：理想振荡器)
    • [E. 相位噪声下 OFDM 雷达的问题陈述](#E. 相位噪声下 OFDM 雷达的问题陈述)
  • [III. PHASE NOISE STATISTICS](#III. PHASE NOISE STATISTICS)
  • • • [A. Statistics of Differential Phase Noise Process](#A. Statistics of Differential Phase Noise Process)
      • [B. 不同振荡器类型的 PN 方差](#B. 不同振荡器类型的 PN 方差)
    • [C. 与时延相关的 PN 协方差矩阵](#C. 与时延相关的 PN 协方差矩阵)
  • [IV. PROPOSED ALGORITHM FOR DELAY-DOPPLER ESTIMATION UNDER PHASE NOISE](#IV. PROPOSED ALGORITHM FOR DELAY-DOPPLER ESTIMATION UNDER PHASE NOISE)
  • • [A. 混合 ML/MAP 估计器](#A. 混合 ML/MAP 估计器)

I. INTRODUCTION

随着下一代无线系统有望在高频段运行，即毫米波 (mmWave) 频段 [11]，硬件损伤 (HWIs)，例如相位噪声 (PN) [16]、功率放大器非线性 (PAN) 和互耦 (MC)，可能成为 OFDM DFRC 系统在雷达和通信两方面性能的主要瓶颈 [17], [18]。特别是，由振荡器不完美引起的 PN 的严重程度 1 ^1 1 会随着工作频率的升高而增加 [19], [21]。由于其快速时变的特性，PN 需要在子载波级（频域）或样本级（时域）进行动态补偿和缓解处理，从而给 OFDM 通信的信道估计和数据检测带来了巨大挑战 [19], [22], [23], [24]。为了解决 OFDM 的 PN 补偿问题，已有各种频域 [21], [25], [26], [27], [28] 和时域 [16], [29], [30] 的估计方法被提出。

1 ^1 1 作为一种时变损伤，PN 对 DFRC 系统构成的文题比由振荡器非理想性引起的静态损伤（如载波频率偏移 (CFO) 和 I/Q 不平衡 [19]）严重得多。例如，CFO 对单站感知系统没有影响，因为发送和接收使用的是同一个振荡器 [20]。

尽管关于 OFDM 通信 中 PN 估计的文献浩如烟海（Despite the vast literature on），但很少有人致力于（very little effort has been devoted to）研究 PN 对 OFDM 雷达 性能的影响（例如 [31], [32]），更不用说开发算法来估计和补偿雷达感知中的 PN 了。

• 在文献 [31] 和 [32] 中，研究了 PN 对 OFDM 雷达距离-速度剖面的影响，结果表明 PN 会导致本底噪声的增加，并在速度轴上产生脊状干扰（ridge along the velocity axis）。

为了支持迈向 6G 网络的新用例，新兴的毫米波感知应用 [33], [34], [35], [36] 对距离和速度精度提出了严格的要求 [37]，这使得必须考虑 PN 的影响。从雷达接收处理的角度来看，现有的 OFDM 雷达算法（例如 [12], [14], [38], [39], [40], [41]）假设振荡器是理想的，因此无法在 PN 影响下，尤其是 PN 方差较大时提供令人满意的性能。

简而言之（In a nutshell），目前尚未有系统的研究来解决带有振荡器 PN 的 OFDM DFRC 系统中的雷达感知问题，也未能推导出联合估计时延、多普勒和 PN 的算法。

作为雷达和通信之间的一个关键区别，所谓的 距离相关效应 （range correlation effect）[42], [43], [44], [45] 构成了单站雷达感知中 PN 与通信设置中 PN 相比的一个本质特性。由于发射机和接收机的 PN 过程是独立的，通信系统中的 PN 统计特性不依赖于未知的信道参数（例如 [16], [19], [46], [47]）。

相反，在共用振荡器的雷达收发机中，对来自目标的反射信号进行下变频会导致一个差分（自参考/自相关）PN 过程 [48], [49]，该过程对应于原始 PN 过程与其经过目标往返时延后的时移版本之间的差值。这种相关效应使得雷达接收机中 PN 的统计特性具有距离依赖性，导致较远目标的 PN 方差更高 [43]，这给雷达感知既带来了挑战也带来了机遇。

• 主要的挑战在于时延和 PN 是耦合的，使得难以解耦相应的估计任务（而在 OFDM 通信的联合信道/PN 估计中通常是这样做的，例如 [29], [50]）。

• 另一方面，主要机遇来自于利用这种距离依赖的 PN 统计特性来增强距离估计性能的可能性。虽然 PN 利用 （PN exploitation）可能提供可观的性能增益，但据作者所知，无论是在标准雷达文献（即调频连续波 (FMCW)、多输入多输出 (MIMO) 或脉冲雷达）中，还是在 OFDM DFRC 研究中，这一主题仍然令人惊讶地未被探索（this topic remains surprisingly unexplored）。

鉴于现有的文献（In light of the existing literature），关于存在 PN 时 OFDM DFRC 系统的感知功能，出现了几个基本问题：

• 对于不同类型的振荡器，即自由运行振荡器 (FROs) 和锁相环 (PLLs) [25], [48]，OFDM 雷达接收机中 PN 的统计特性是什么？
• 我们如何开发强大的算法来联合估计时延、多普勒和 PN，以 缓解 PN 对感知性能的影响？FRO 和 PLL 如何影响时延和多普勒估计的性能？
• 考虑到距离相关效应，是否可能 利用 PN 来提高测距性能，使其超越使用无 PN 理想振荡器所能达到的性能？

为了试图回答这些问题（In an attempt to answer these questions），本文研究了在面临振荡器 PN 时 OFDM DFRC 系统中的雷达时延-多普勒估计问题。

• 我们首先推导了针对 FRO 和 PLL 的 OFDM 雷达观测中 PN 的统计特性。
• 然后，我们提出了一种基于混合最大似然 (ML)/MAP 估计器代价函数中 PN 迭代小角度近似的新型算法，用于联合估计时延、多普勒和 PN，该算法能够快速收敛到相应的理论界限。
• 此外，我们开发了一种 PN 利用方法，可以有效地利用距离依赖的 PN 统计特性来解决距离模糊问题。

本文的主要贡献总结如下：

• PN 下 OFDM 雷达感知的问题公式化：我们在文献中首次研究了振荡器 PN 影响下 OFDM DFRC 系统中的单站雷达感知问题。为了提供严格的问题公式化，我们推导了 OFDM 雷达接收机中 PN 的显式统计特性描述。我们考虑了两种常用的振荡器模型，即 FRO 和 PLL。推导揭示了前者的 PN 协方差矩阵具有块对角结构，而后者具有更一般的 Toeplitz-块 Toeplitz 结构。

• 通过迭代小角度近似算法实现的混合 ML/MAP 估计器：我们推导了包含多个符号的 OFDM 帧上的确定性时延-多普勒参数和随机 PN 的混合 ML/MAP 估计器。反向散射信号中 PN 的协方差矩阵取决于未知的时延。为了处理由此产生的代价函数的高度非线性，我们提出了一种新颖的迭代小角度近似 (ISAA) 方法，该方法在每次迭代中调用当前 PN 估计值周围的小 PN 近似，逐步优化时延-多普勒-PN 的估计并最小化残余 PN 的影响。所提出的方法实现了作为时延-多普勒函数的 PN 的闭式更新，并通过交替迭代显著提高了 PN 跟踪精度。

• 利用 PN 解决距离模糊：基于 PN 通过其距离依赖的统计特性携带了有价值的时延信息这一关键见解，我们开发了一种解决距离模糊的算法，该算法利用了所提出的 ISAA 方法输出的 PN 估计值的统计特性。这种 PN 利用方法通过利用 Toeplitz-块 Toeplitz 结构，将距离估计公式化为一个参数化协方差矩阵重构问题，并能够通过 PN 协方差在距离上不存在模糊性这一事实（与由 OFDM 子载波间隔决定的基本上限相反 [12], [39], [51]）产生无模糊的距离估计。

• 仿真分析 ：在各种工作条件下进行的大量仿真表明，所提出的 ISAA 算法仅需几次迭代即可快速收敛到相应的关于时延-多普勒-PN 估计的混合克拉美罗界 (CRBs) [52], [53]，并且性能显著优于基准 FFT 方法 [12], [39], [40]。在更高的信噪比 (SNR)、更大的 3 dB 振荡器带宽、更小的环路带宽（针对 PLL）以及更远的目标距离下，精度增益更为明显。此外，我们发现 PLL 对多普勒估计比 FRO 更有利，这是因为 PLL 存在慢时间 PN 相关性。此外，在特定的 SNR 水平之上，PN 利用算法显示出能够正确识别距离模糊目标的真实距离，并且实现了比使用无 PN 观测值的 FFT 方法高得多的测距精度，从而将 PN 转化为感知的优势 2 ^2 2。

符号说明： Π X = X ( X H X ) − 1 X H \mathbf{\Pi}{\mathbf{X}} = \mathbf{X}(\mathbf{X}^H \mathbf{X})^{-1}\mathbf{X}^H ΠX=X(XHX)−1XH 表示向 X \mathbf{X} X 的列空间的正交投影，而 Π X ⊥ = I − Π X \mathbf{\Pi}{\mathbf{X}}^{\perp} = \mathbf{I} - \mathbf{\Pi}{\mathbf{X}} ΠX⊥=I−ΠX。 ⊙ \odot ⊙ 和 ⊗ \otimes ⊗ 分别表示阿达玛 (Hadamard) 积和克罗内克 (Kronecker) 积。 d i a g ( x ) \mathrm{diag}(\mathbf{x}) diag(x) 输出一个以向量 x \mathbf{x} x 的元素为对角线的对角矩阵， d i a g ( X ) \mathrm{diag}(\mathbf{X}) diag(X) 表示一个以方阵 X \mathbf{X} X 的对角元素为对角线的对角矩阵， v e c ( ⋅ ) \mathrm{vec}(\cdot) vec(⋅) 表示矩阵向量化算子， r e s h a p e N , M ( ⋅ ) \mathrm{reshape}{N, M}(\cdot) reshapeN,M(⋅) 将一个向量重塑为一个 N × M N \times M N×M 的矩阵。

II. SYSTEM MODEL AND PROBLEM FORMULATION

考虑一个由 DFRC 收发机和一个通信接收机 (RX) 组成的 OFDM JRC 系统，如图 1 所示。DFRC 收发机在单个硬件平台上配备了雷达通信发射机 (TX)（即传统的 OFDM TX）和雷达 RX，它向通信 RX 发送数据符号，同时利用后向散射信号执行单站雷达感知，以完成各种雷达任务（例如，目标检测、估计、跟踪和分类）[2], [8], [12]。

为了实现全双工操作且不对雷达 RX 造成自干扰，我们假设 DFRC 收发处的 TX/RX 天线具有足够的隔离度和去耦 [6], [12], [39], [54], [55], [56]。在通信 RX 处，常规的 OFDM 接收操作（例如，信道估计、频率同步、数据检测 [24]）照常执行，不受感知功能的任何约束。

此外，DFRC 收发机的振荡器（在联合设计的硬件平台上由 TX 和雷达 RX 共享）被假设为非理想的，并且由于不完美而受到 PN 的损伤 [19], [21], [25], [46], [57]。

在本节中，我们推导了存在 PN 时的 OFDM 发射和雷达接收信号模型，并建立了由此产生的 OFDM 雷达感知问题。我们注意到，本文将重点关注 PN 下的雷达感知，而假设通信 RX 通过成熟的方法（例如 [16], [22], [30], [58]）来补偿 PN。

A. Transmit Signal Model

我们考虑一个包含 M M M 个符号和 N N N 个子载波的 OFDM 通信帧。一个符号的总持续时间由 T s y m = T c p + T T_{\mathrm{sym}} = T_{\mathrm{cp}} + T Tsym=Tcp+T 给出，其中 T c p T_{\mathrm{cp}} Tcp 和 T T T 分别表示循环前缀 (CP) 和基本符号持续时间 [12]。此外， Δ f = 1 / T \Delta f = 1/T Δf=1/T 是子载波间隔，导致总带宽为 N Δ f = B N\Delta f = B NΔf=B。复基带 OFDM 发射信号可以表示为 [13]

s ( t ) = ∑ m = 0 M − 1 s m ( t ) , (1) s(t) = \sum_{m=0}^{M-1} s_m(t), \tag{1} s(t)=m=0∑M−1sm(t),(1)

其中

s m ( t ) = 1 N ∑ n = 0 N − 1 x n , m e j 2 π n Δ f t r e c t ( t − m T s y m T s y m ) (2) s_m(t) = \frac{1}{\sqrt{N}} \sum_{n=0}^{N-1} x_{n,m} e^{j2\pi n \Delta f t} \mathrm{rect}\left( \frac{t - m T_{\mathrm{sym}}}{T_{\mathrm{sym}}} \right) \tag{2} sm(t)=N 1n=0∑N−1xn,mej2πnΔftrect(Tsymt−mTsym)(2)

是第 m m m 个符号的 OFDM 信号， x n , m x_{n,m} xn,m 表示第 m m m 个符号的第 n n n 个子载波上的复数据符号， r e c t ( t ) \mathrm{rect}(t) rect(t) 是一个矩形脉冲，当 t ∈ [ 0 , 1 ] t \in [0, 1] t∈[0,1] 时取值为 1 1 1，否则为 0 0 0。在振荡器存在 PN 的情况下，这块 M M M 个符号在 t ∈ [ 0 , M T s y m ] t \in [0, MT_{\mathrm{sym}}] t∈[0,MTsym] 期间的上变频发射信号（the upconverted transmit signal）可以写为 [49]

s ~ ( t ) = ℜ { s ( t ) e j [ 2 π f c t + ϕ ( t ) ] } , (3) \widetilde{s}(t) = \Re \left\{ s(t) e^{j[2\pi f_c t + \phi(t)]} \right\}, \tag{3} s (t)=ℜ{s(t)ej[2πfct+ϕ(t)]},(3)

其中 f c f_c fc 是（is）载波频率， ϕ ( t ) \phi(t) ϕ(t) 表示（denotes）振荡器中的 PN 过程。

B. Receive Signal Model

在雷达感知中，我们假设远场存在一个点目标，其具有往返时延 τ = 2 R / c \tau = 2R/c τ=2R/c，归一化多普勒频移 ν = 2 v / c \nu = 2v/c ν=2v/c 以及复信道增益 α \alpha α（包含路径损耗和雷达散射截面效应）。在此， R , v R, v R,v 和 c c c 分别表示距离、径向速度和传播速度。给定 (3) 中的发射信号模型，雷达接收机处的通带后向散射信号可以表示为

y ~ ( t ) = ℜ { α s ( t − τ ( t ) ) e j [ 2 π f c ( t − τ ( t ) ) + ϕ ( t − τ ( t ) ) ] } , (4) \widetilde{y}(t) = \Re\left\{\alpha s(t - \tau(t))e^{j[2\pi f_c(t-\tau(t))+\phi(t-\tau(t))]}\right\}, \tag{4} y (t)=ℜ{αs(t−τ(t))ej[2πfc(t−τ(t))+ϕ(t−τ(t))]},(4)

其中 τ ( t ) = τ − ν t \tau(t) = \tau - \nu t τ(t)=τ−νt 是由多普勒频移引起的时变时延。通过有噪声的振荡器对 (4) 中的通带信号进行下变频后（对应于乘以 e − j ( 2 π f c t + ϕ ( t ) ) e^{-j(2\pi f_c t + \phi(t))} e−j(2πfct+ϕ(t)) [59]），等效复基带信号可以写为 [44]

y ( t ) = α s ( t − τ ( t ) ) e j [ 2 π f c ( t − τ ( t ) ) + ϕ ( t − τ ( t ) ) ] e − j [ 2 π f c t + ϕ ( t ) ] = α s ( t − τ ( t ) ) e − j 2 π f c τ e j 2 π f c ν t e j [ ϕ ( t − τ ( t ) ) − ϕ ( t ) ] . (5) \begin{aligned} y(t) &= \alpha s(t - \tau(t))e^{j[2\pi f_c(t-\tau(t))+\phi(t-\tau(t))]}e^{-j[2\pi f_c t+\phi(t)]} \\ &= \alpha s(t - \tau(t))e^{-j2\pi f_c \tau} e^{j2\pi f_c \nu t} e^{j[\phi(t-\tau(t))-\phi(t)]}. \end{aligned} \tag{5} y(t)=αs(t−τ(t))ej[2πfc(t−τ(t))+ϕ(t−τ(t))]e−j[2πfct+ϕ(t)]=αs(t−τ(t))e−j2πfcτej2πfcνtej[ϕ(t−τ(t))−ϕ(t)].(5)

• ( t − τ ( t ) ) (t - \tau(t)) (t−τ(t)) (核心变量：往返时延)：
  • 这是公式中最关键的变量。雷达在时刻 t t t 接收到的信号，并不是时刻 t t t 发出的，而是时刻 t − τ ( t ) t - \tau(t) t−τ(t) 发出的。
  • τ ( t ) \tau(t) τ(t) 是时变时延。因为目标在运动（有多普勒速度），所以信号飞行的距离在变化，导致时延 τ \tau τ 也是时间 t t t 的函数。
• e j [ ...   ] e^{j[\dots]} ej[...] (载波与相位项)：这里面包含了三个频率/相位成分的延迟版本：

  1. 2 π f c ( t − τ ( t ) ) 2\pi f_c (t - \tau(t)) 2πfc(t−τ(t))：这是载波相位。

     • 发射时载波是 e j 2 π f c t e^{j2\pi f_c t} ej2πfct。
     • 接收时，我们收到的是 τ ( t ) \tau(t) τ(t) 时刻之前的载波状态，
     • 所以 t t t 变成了 t − τ ( t ) t-\tau(t) t−τ(t)。正是这一项展开后产生了多普勒频移（ e − j 2 π f c τ ( t ) = e − j 2 π f c ( τ − ν t ) = Const ⋅ e j 2 π f c ν t e^{-j2\pi f_c \tau(t)} = e^{-j2\pi f_c (\tau - \nu t)} = \text{Const} \cdot e^{j2\pi f_c \nu t} e−j2πfcτ(t)=e−j2πfc(τ−νt)=Const⋅ej2πfcνt）。

  2. ϕ ( t − τ ( t ) ) \phi(t - \tau(t)) ϕ(t−τ(t)) (相位噪声)：

     • 这是本论文的研究重点。相位噪声 ϕ ( t ) \phi(t) ϕ(t) 是振荡器自带的随机抖动。
     • 关键点：雷达在时刻 t t t "听到"的相位噪声，不是接收机当前时刻 t t t 的振荡器噪声，而是发射机在过去时刻 t − τ ( t ) t-\tau(t) t−τ(t) 发射信号那一瞬间附带在信号上的噪声。

主要关注车载 JRC 场景，我们假设归一化多普勒频移满足 ∣ ν ∣ ≪ 1 / N |\nu| \ll 1/N ∣ν∣≪1/N [14], [20], [38]，其中对于典型的车载 OFDM JRC 系统， ∣ ν ∣ ≪ 10 − 6 |\nu| \ll 10^{-6} ∣ν∣≪10−6（对应于速度 ∣ v ∣ ≪ 540 |v| \ll 540 ∣v∣≪540 km/h），而 N N N 的数量级为 10 3 10^3 103。这允许我们将 (5) 中的相位噪声项近似为 ϕ ( t − τ ( t ) ) ≈ ϕ ( t − τ ) \phi(t - \tau(t)) \approx \phi(t - \tau) ϕ(t−τ(t))≈ϕ(t−τ)。此外，时间-带宽积 B M T s y m BMT_{\mathrm{sym}} BMTsym 足够小，可以（连同 ∣ ν ∣ ≪ 1 / N |\nu| \ll 1/N ∣ν∣≪1/N 一起）证明窄带近似 s ( t − τ ( t ) ) ≈ s ( t − τ ) s(t - \tau(t)) \approx s(t - \tau) s(t−τ(t))≈s(t−τ) [51] 的合理性。在此设置下，(5) 中的接收信号变为

y ( t ) = α s ( t − τ ) e − j 2 π f c τ e j 2 π f c ν t w ( t , τ ) , (6) y(t) = \alpha s(t - \tau)e^{-j2\pi f_c \tau} e^{j2\pi f_c \nu t} w(t, \tau), \tag{6} y(t)=αs(t−τ)e−j2πfcτej2πfcνtw(t,τ),(6)

其中乘性相位噪声过程表示为

w ( t , τ ) ≜ e j [ ϕ ( t − τ ) − ϕ ( t ) ] . (7) w(t, \tau) \triangleq e^{j[\phi(t-\tau)-\phi(t)]}. \tag{7} w(t,τ)≜ej[ϕ(t−τ)−ϕ(t)].(7)

(7) 中相位噪声过程 ϕ ( t − τ ) − ϕ ( t ) \phi(t - \tau) - \phi(t) ϕ(t−τ)−ϕ(t) 的统计特性将在第三节中推导。

C. Fast-Time/Slow-Time Representation With Phase Noise

对于第 m m m 个符号，我们移除 CP 并在 t = m T s y m + T c p + ℓ T / N t = m T_{\mathrm{sym}} + T_{\mathrm{cp}} + \ell T / N t=mTsym+Tcp+ℓT/N（其中 ℓ = 0 , ... , N − 1 \ell = 0, \ldots, N-1 ℓ=0,...,N−1）处对 (6) 中的 y ( t ) y(t) y(t) 进行采样。采用标准的 OFDM 雷达假设 T c p ≥ τ T_{\mathrm{cp}} \geq \tau Tcp≥τ [1], [38], [39]（CP 持续时间设置为长于最远目标的往返时延）和 f c T ν ≪ 1 f_c T \nu \ll 1 fcTν≪1 [15], [60], [61], [62]（多普勒频移 f c ν f_c \nu fcν 与子载波间隔 Δ f \Delta f Δf 相比很小），并忽略常数相位项，第 m m m 个符号的接收信号可以写为 [14], [20]

y ℓ , m = α e j 2 π f c m T s y m ν w ℓ , m ( τ ) × 1 N ∑ n = 0 N − 1 x n , m e j 2 π n ℓ N e − j 2 π n Δ f τ , (8) y_{\ell, m} = \alpha e^{j 2 \pi f_c m T_{\mathrm{sym}} \nu} w_{\ell, m}(\tau) \times \frac{1}{\sqrt{N}} \sum_{n=0}^{N-1} x_{n, m} e^{j 2 \pi n \frac{\ell}{N}} e^{-j 2 \pi n \Delta f \tau}, \tag{8} yℓ,m=αej2πfcmTsymνwℓ,m(τ)×N 1n=0∑N−1xn,mej2πnNℓe−j2πnΔfτ,(8)

其中 w ℓ , m ( τ ) w_{\ell, m}(\tau) wℓ,m(τ) 是 (6) 中 PN 项 w ( t , τ ) w(t, \tau) w(t,τ) 在 t = m T s y m + T c p + ℓ T / N t = m T_{\mathrm{sym}} + T_{\mathrm{cp}} + \ell T / N t=mTsym+Tcp+ℓT/N 处的采样版本。令

b ( τ ) ≜ [ 1 , e − j 2 π Δ f τ , ... , e − j 2 π ( N − 1 ) Δ f τ ] T , (9) \mathbf{b}(\tau) \triangleq \left[ 1, e^{-j 2 \pi \Delta f \tau}, \ldots, e^{-j 2 \pi(N-1) \Delta f \tau} \right]^T, \tag{9} b(τ)≜[1,e−j2πΔfτ,...,e−j2π(N−1)Δfτ]T,(9) c ( ν ) ≜ [ 1 , e − j 2 π f c T s y m ν , ... , e − j 2 π f c ( M − 1 ) T s y m ν ] T , (10) \mathbf{c}(\nu) \triangleq \left[ 1, e^{-j 2 \pi f_c T_{\mathrm{sym}} \nu}, \ldots, e^{-j 2 \pi f_c(M-1) T_{\mathrm{sym}} \nu} \right]^T, \tag{10} c(ν)≜[1,e−j2πfcTsymν,...,e−j2πfc(M−1)Tsymν]T,(10)

分别表示频域和时间（慢时间）导向矢量。

对 (8) 中的观测值在快时间 ℓ \ell ℓ 和慢时间 m m m 上进行聚合，并考虑到加性传感器噪声的存在，可以得到存在 PN 时的快时间/慢时间观测矩阵为 [20]

Y = α W ⊙ F N H ( X ⊙ b ( τ ) c H ( ν ) ) + Z , (11) \mathbf{Y} = \alpha \mathbf{W} \odot \mathbf{F}_N^H \left( \mathbf{X} \odot \mathbf{b}(\tau) \mathbf{c}^H(\nu) \right) + \mathbf{Z}, \tag{11} Y=αW⊙FNH(X⊙b(τ)cH(ν))+Z,(11)

其中

• W ∈ C N × M \mathbf{W} \in \mathbb{C}^{N \times M} W∈CN×M（其元素为 [ W ] ℓ , m ≜ w ℓ , m ( τ ) [\mathbf{W}]{\ell, m} \triangleq w{\ell, m}(\tau) [W]ℓ,m≜wℓ,m(τ)）是由 (7) 中 PN 过程的快时间/慢时间样本组成的 乘性 PN 矩阵 3 ^3 3，
• F N ∈ C N × N \mathbf{F}_N \in \mathbb{C}^{N \times N} FN∈CN×N 是酉 DFT 矩阵，其元素为 [ F N ] ℓ , n = 1 N e − j 2 π n ℓ N [\mathbf{F}N]{\ell, n} = \frac{1}{\sqrt{N}} e^{-j 2 \pi n \frac{\ell}{N}} [FN]ℓ,n=N 1e−j2πnNℓ，
• X ∈ C N × M \mathbf{X} \in \mathbb{C}^{N \times M} X∈CN×M 包含复数据符号，其元素为 [ X ] n , m ≜ x n , m [\mathbf{X}]{n, m} \triangleq x{n, m} [X]n,m≜xn,m，
• Y ∈ C N × M \mathbf{Y} \in \mathbb{C}^{N \times M} Y∈CN×M 的元素为 [ Y ] ℓ , m ≜ y ℓ , m [\mathbf{Y}]{\ell, m} \triangleq y{\ell, m} [Y]ℓ,m≜yℓ,m，
• 而 Z ∈ C N × M \mathbf{Z} \in \mathbb{C}^{N \times M} Z∈CN×M 是加性高斯白噪声 (AWGN)，满足 v e c ( Z ) ∼ C N ( 0 , 2 σ 2 I ) \mathrm{vec}(\mathbf{Z}) \sim \mathcal{CN}(\mathbf{0}, 2 \sigma^2 \mathbf{I}) vec(Z)∼CN(0,2σ2I)。

正如从 (11) 中观察到的那样，PN 分量 W \mathbf{W} W 在 OFDM 雷达中引入了载波间干扰 (ICI) [14], [20], [51]（类似于其在 OFDM 通信中的影响 [16], [19], [21], [25]），并且可能会严重降低时延-多普勒估计的性能。

从公式 (8) 到 (11) 的矩阵化推导

1. 定义矩阵与向量

根据索引 ( n , m ) (n, m) (n,m) 和 ( ℓ , m ) (\ell, m) (ℓ,m) 定义以下矩阵元素：

• 数据矩阵 X ∈ C N × M \mathbf{X} \in \mathbb{C}^{N \times M} X∈CN×M： [ X ] n , m = x n , m [\mathbf{X}]{n,m} = x{n,m} [X]n,m=xn,m
• 时延导向矢量 b ( τ ) \mathbf{b}(\tau) b(τ)： [ b ( τ ) ] n = e − j 2 π n Δ f τ [\mathbf{b}(\tau)]_n = e^{-j 2 \pi n \Delta f \tau} [b(τ)]n=e−j2πnΔfτ
• 多普勒导向矢量 c ( ν ) \mathbf{c}(\nu) c(ν)： [ c ( ν ) ] m = e − j 2 π f c m T s y m ν [\mathbf{c}(\nu)]m = e^{-j 2 \pi f_c m T{\mathrm{sym}} \nu} [c(ν)]m=e−j2πfcmTsymν (注意 c H \mathbf{c}^H cH 引入共轭)
• 相位噪声矩阵 W \mathbf{W} W： [ W ] ℓ , m = w ℓ , m ( τ ) [\mathbf{W}]{\ell, m} = w{\ell, m}(\tau) [W]ℓ,m=wℓ,m(τ)

2. 频域信号重构 (Hadamard 积)

分析公式 (8) 中的频域核心项，其由数据、时延相移和多普勒相移组成：
Term n , m = x n , m ⋅ e − j 2 π n Δ f τ ⏟ [ b ] n ⋅ e j 2 π f c m T s y m ν ⏟ [ c H ] m \text{Term}{n,m} = x{n,m} \cdot \underbrace{e^{-j 2 \pi n \Delta f \tau}}{[\mathbf{b}]n} \cdot \underbrace{e^{j 2 \pi f_c m T{\mathrm{sym}} \nu}}{[\mathbf{c}^H]_m} Termn,m=xn,m⋅[b]n e−j2πnΔfτ⋅[cH]m ej2πfcmTsymν

这对应于数据矩阵 X \mathbf{X} X 与时延-多普勒秩-1矩阵的点乘：
A = X ⊙ ( b ( τ ) c H ( ν ) ) \mathbf{A} = \mathbf{X} \odot \left( \mathbf{b}(\tau) \mathbf{c}^H(\nu) \right) A=X⊙(b(τ)cH(ν))

3. 时域变换 (IDFT)

公式 (8) 中对 n n n 的求和 1 N ∑ n = 0 N − 1 ( ...   ) e j 2 π n ℓ N \frac{1}{\sqrt{N}} \sum_{n=0}^{N-1} (\dots) e^{j 2 \pi n \frac{\ell}{N}} N 1∑n=0N−1(...)ej2πnNℓ 等效于对矩阵 A \mathbf{A} A 的每一列执行 IDFT 操作。这在矩阵代数中表示为左乘 IDFT 矩阵 F N H \mathbf{F}_N^H FNH。 F N \mathbf{F}_N FN 是标准 DFT 矩阵，其元素为 [ F N ] ℓ , n = 1 N e − j 2 π n ℓ N [\mathbf{F}N]{\ell, n} = \frac{1}{\sqrt{N}} e^{-j 2 \pi n \frac{\ell}{N}} [FN]ℓ,n=N 1e−j2πnNℓ，则其共轭转置 [ F N H ] ℓ , n [\mathbf{F}N^H]{\ell, n} [FNH]ℓ,n 的元素为 1 N e j 2 π n ℓ N \frac{1}{\sqrt{N}} e^{j 2 \pi n \frac{\ell}{N}} N 1ej2πnNℓ：
G = F N H A = F N H ( X ⊙ b ( τ ) c H ( ν ) ) \mathbf{G} = \mathbf{F}_N^H \mathbf{A} = \mathbf{F}_N^H \left( \mathbf{X} \odot \mathbf{b}(\tau) \mathbf{c}^H(\nu) \right) G=FNHA=FNH(X⊙b(τ)cH(ν))

4. 时域加权与噪声 (最终组合)

公式 (8) 的外部项为幅度 α \alpha α 和时变相位噪声 w ℓ , m w_{\ell, m} wℓ,m，这对应于在时域矩阵上进行点乘 (Hadamard 积)。考虑到加性噪声矩阵 Z \mathbf{Z} Z，接收信号矩阵为：
Y = α W ⊙ G + Z \mathbf{Y} = \alpha \mathbf{W} \odot \mathbf{G} + \mathbf{Z} Y=αW⊙G+Z

将步骤 3 中的 G \mathbf{G} G 代入，即得到最终的紧凑矩阵形式公式 (11)：
Y = α W ⊙ F N H ( X ⊙ b ( τ ) c H ( ν ) ) + Z (11) \mathbf{Y} = \alpha \mathbf{W} \odot \mathbf{F}_N^H \left( \mathbf{X} \odot \mathbf{b}(\tau) \mathbf{c}^H(\nu) \right) + \mathbf{Z} \tag{11} Y=αW⊙FNH(X⊙b(τ)cH(ν))+Z(11)

D. 特例：理想振荡器

为了将 (11) 中推导出的信号模型与文献中常用的模型联系起来，我们研究了理想振荡器的特例，其中不存在 PN 过程，即 ϕ ( t ) = 0 , ∀ t \phi(t) = 0, \forall t ϕ(t)=0,∀t，这得出 w ( t , τ ) = 1 , ∀ t , τ w(t, \tau) = 1, \forall t, \tau w(t,τ)=1,∀t,τ，并且 W \mathbf{W} W 变为全 1 矩阵，即 W = 1 N × M \mathbf{W} = \mathbf{1}_{N \times M} W=1N×M。在这种情况下，(11) 恢复为无 PN 模型

Y P N − f r e e = α F N H ( X ⊙ b ( τ ) c H ( ν ) ) + Z . (12) \mathbf{Y}^{\mathrm{PN-free}} = \alpha \mathbf{F}_N^H \left( \mathbf{X} \odot \mathbf{b}(\tau)\mathbf{c}^H(\nu) \right) + \mathbf{Z}. \tag{12} YPN−free=αFNH(X⊙b(τ)cH(ν))+Z.(12)

遵循 OFDM 雷达接收机的传统处理链 [12], [39], [40]（Following the traditional processing chain for OFDM radar receivers），我们对 (12) 中 Y P N − f r e e \mathbf{Y}^{\mathrm{PN-free}} YPN−free 的列进行 DFT，以便从快时间/慢时间域切换到频率/慢时间域，并获得标准的 OFDM 雷达观测值（obtain the standard OFDM

radar observations） [12], [15], [39], [40], [60], [61]：

Y ~ = F N Y P N − f r e e = α X ⊙ b ( τ ) c H ( ν ) + F N Z , (13) \widetilde{\mathbf{Y}} = \mathbf{F}_N \mathbf{Y}^{\mathrm{PN-free}} = \alpha \mathbf{X} \odot \mathbf{b}(\tau)\mathbf{c}^H(\nu) + \mathbf{F}_N \mathbf{Z}, \tag{13} Y =FNYPN−free=αX⊙b(τ)cH(ν)+FNZ,(13)

其中 v e c ( F N Z ) ∼ C N ( 0 , 2 σ 2 I ) \mathrm{vec}(\mathbf{F}_N \mathbf{Z}) \sim \mathcal{CN}(\mathbf{0}, 2\sigma^2\mathbf{I}) vec(FNZ)∼CN(0,2σ2I)。显然，(13) 不涉及任何 ICI 效应，因此适合采用传统的时延-多普勒估计算法（在去除 X \mathbf{X} X 的影响后），例如时间和频率域上的二维 DFT [12], [39], [40] 和超分辨率方法 [60], [61]。

E. 相位噪声下 OFDM 雷达的问题陈述

给定发射数据符号 X \mathbf{X} X 和 (11) 中的快时间/慢时间观测值 Y \mathbf{Y} Y，存在 PN 时的 OFDM 雷达感知感兴趣的问题是估计目标参数 α , τ \alpha, \tau α,τ 和 ν \nu ν，这本质上涉及估计 PN 矩阵 W \mathbf{W} W 并补偿其对 Y \mathbf{Y} Y 的影响。为了解决这个问题，我们首先在第三节中推导 PN 过程的统计特性，然后在第四节中利用这些特性提出一种联合估计时延、多普勒和 PN 的新算法。在第五节中，我们将进一步利用 PN 作为对雷达感知有益的因素。

III. PHASE NOISE STATISTICS

本节提供（provides）了 (7) 中 PN 过程 ϕ ( t − τ ) − ϕ ( t ) \phi(t - \tau) - \phi(t) ϕ(t−τ)−ϕ(t) 的统计特性描述，给出了（gives expressions of）不同类型振荡器的 PN 方差表达式，并推导了（derives） PN 协方差矩阵的结构。

A. Statistics of Differential Phase Noise Process

令 ϕ ( t ) \phi(t) ϕ(t) 为均值为零、方差为 σ ϕ 2 ( t ) \sigma_{\phi}^2(t) σϕ2(t) 的高斯随机过程 [30], [49]，即

ϕ ( t ) ∼ N ( 0 , σ ϕ 2 ( t ) ) , (14) \phi(t) \sim \mathcal{N}(0, \sigma_{\phi}^2(t)), \tag{14} ϕ(t)∼N(0,σϕ2(t)),(14)

其中 σ ϕ 2 ( t ) \sigma_{\phi}^2(t) σϕ2(t) 的形式取决于振荡器的类型。我们将 差分 PN (differential PN，DPN) 过程 [63]（也称为 自参考 PN 、增量 PN 过程 [48] 或 PN 变化 [49]）定义为

ξ ( t , τ ) ≜ ϕ ( t ) − ϕ ( t − τ ) . (15) \xi(t, \tau) \triangleq \phi(t) - \phi(t - \tau). \tag{15} ξ(t,τ)≜ϕ(t)−ϕ(t−τ).(15)

由于 DPN 过程是平稳的，其统计特性仅取决于增量值（目标时延） τ \tau τ [48, Sec. IV]。因此，DPN 过程的统计特性可以描述为 [49]

ξ ( t , τ ) ∼ N ( 0 , σ ξ 2 ( τ ) ) , (16) \xi(t, \tau) \sim \mathcal{N}(0, \sigma_{\xi}^2(\tau)), \tag{16} ξ(t,τ)∼N(0,σξ2(τ)),(16)

其中 σ ξ 2 ( τ ) \sigma_{\xi}^2(\tau) σξ2(τ) 是 ξ ( t , τ ) \xi(t, \tau) ξ(t,τ) 与时延相关的方差。以下引理提供了 ξ ( t , τ ) \xi(t, \tau) ξ(t,τ) 的二阶统计量。

引理 1 ：(15) 中 DPN 过程 ξ ( t , τ ) \xi(t, \tau) ξ(t,τ) 的相关函数由下式给出
R ξ ξ ( Δ t , τ ) = R ξ ξ ( t 1 , t 2 , τ ) ≜ E [ ξ ( t 1 , τ ) ξ ( t 2 , τ ) ] = σ ξ 2 ( τ + Δ t ) + σ ξ 2 ( τ − Δ t ) 2 − σ ξ 2 ( Δ t ) , (17) \begin{aligned} R_{\xi\xi}(\Delta t, \tau) &= R_{\xi\xi}(t_1, t_2, \tau) \triangleq \mathbb{E}\left[ \xi(t_1, \tau)\xi(t_2, \tau) \right] \\ &= \frac{\sigma_{\xi}^2(\tau + \Delta t) + \sigma_{\xi}^2(\tau - \Delta t)}{2} - \sigma_{\xi}^2(\Delta t), \end{aligned} \tag{17} Rξξ(Δt,τ)=Rξξ(t1,t2,τ)≜E[ξ(t1,τ)ξ(t2,τ)]=2σξ2(τ+Δt)+σξ2(τ−Δt)−σξ2(Δt),(17)

其中 Δ t ≜ t 1 − t 2 \Delta t \triangleq t_1 - t_2 Δt≜t1−t2 是时间差。

证明：请参阅补充材料中的 S-I 节。

B. 不同振荡器类型的 PN 方差

引理 1 允许我们根据与时延相关的方差函数 σ ξ 2 ( τ ) \sigma_{\xi}^2(\tau) σξ2(τ) 来计算 ξ ( t , τ ) \xi(t, \tau) ξ(t,τ) 的相关性。我们现在通过区分振荡器的两种实现形式，即自由运行振荡器 (FRO) 和锁相环 (PLL) 合成器 [25], [48]，来提供 σ ξ 2 ( τ ) \sigma_{\xi}^2(\tau) σξ2(τ) 的表达式。

1. 自由运行振荡器 (FROs) ：对于 FRO，(16) 中 DPN ξ ( t , τ ) \xi(t, \tau) ξ(t,τ) 的方差由下式给出 [48, Sec. V], [49, Sec. V, VI], [25, Sec. III-A]

σ ξ 2 ( τ ) = 4 π f 3   d B ∣ τ ∣ , (18) \sigma_{\xi}^2(\tau) = 4\pi f_{3\,\mathrm{dB}} |\tau|, \tag{18} σξ2(τ)=4πf3dB∣τ∣,(18)

其中 f 3   d B f_{3\,\mathrm{dB}} f3dB 是洛伦兹振荡器（Lorentzian oscillator）频谱的 3 dB 带宽。

2. 锁相环 (PLL) 合成器：对于 PLL 架构，(16) 中与时延相关的方差可以表示为 [48, Sec. VII-A], [49, Sec. III]

σ ξ 2 ( τ ) = 2 f 3   d B f l o o p ( 1 − e − 2 π f l o o p ∣ τ ∣ ) , (19) \sigma_{\xi}^2(\tau) = \frac{2 f_{3\,\mathrm{dB}}}{f_{\mathrm{loop}}} \left( 1 - e^{-2\pi f_{\mathrm{loop}} |\tau|} \right), \tag{19} σξ2(τ)=floop2f3dB(1−e−2πfloop∣τ∣),(19)

其中 f l o o p f_{\mathrm{loop}} floop 表示 PLL 的环路带宽。

我们注意到，随着 f l o o p f_{\mathrm{loop}} floop 的减小，PLL 退化为 FRO，即当 f l o o p → 0 f_{\mathrm{loop}} \to 0 floop→0 时，(19) 收敛至 (18)。利用表达式 (18) 和 (19)，可以通过 (16) 和 (17) 获得针对 FRO 和 PLL 的 ξ ( t , τ ) \xi(t, \tau) ξ(t,τ) 的完整统计特性描述，进而得出 (11) 中 W \mathbf{W} W 内快时间/慢时间 PN 样本的协方差矩阵。作为一个例子，图 2 绘制了针对 PLL 和 FRO 在不同目标时延 τ \tau τ 下 ξ ( t , τ ) \xi(t, \tau) ξ(t,τ) 的协方差。该图阐明了 OFDM 雷达感知中 PN 统计特性的时延依赖性（与 OFDM 通信相反，例如 [19], [46], [47]），并提供了关于基于 PLL 的控制对 PN 相关行为影响的见解。

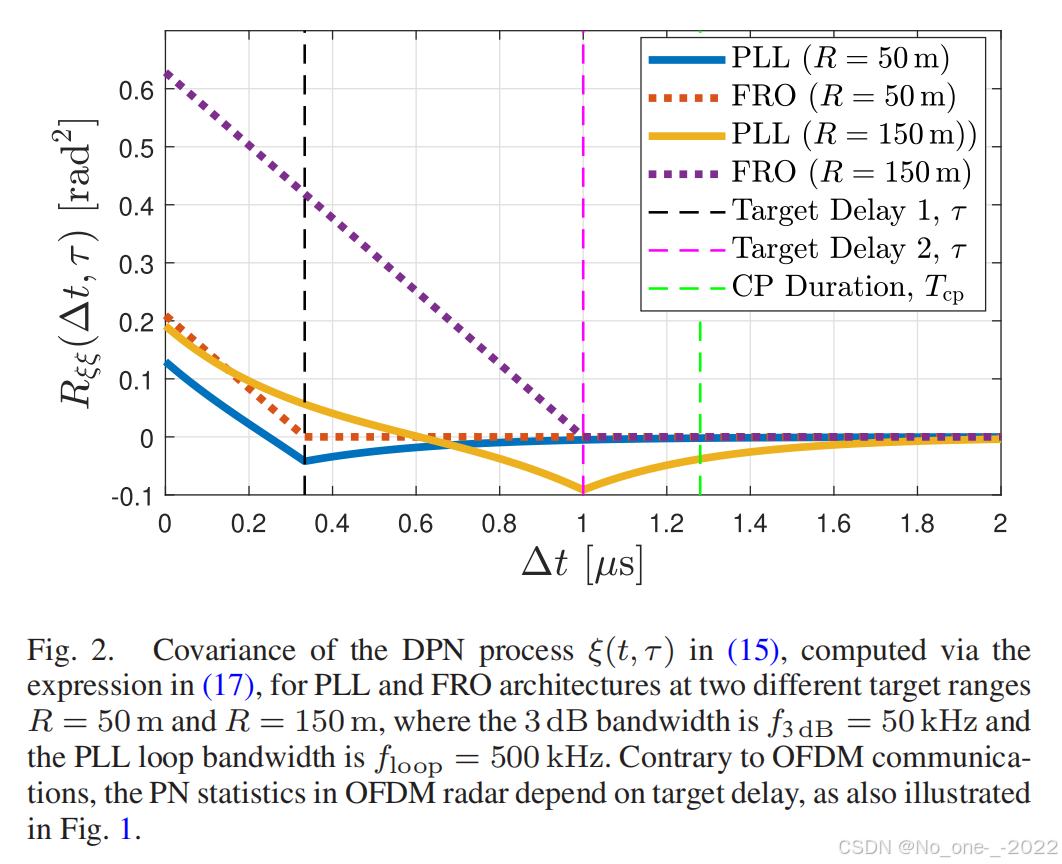
图 2. DPN 过程 ξ ( t , τ ) \xi(t, \tau) ξ(t,τ)（定义见 (15)）的协方差，该协方差是通过 (17) 中的表达式针对 PLL 和 FRO 架构在两个不同的目标距离 R = 50 R = 50 R=50 m 和 R = 150 R = 150 R=150 m 下计算得出的，其中 3 dB 带宽为 f 3   d B = 50 f_{3\,\mathrm{dB}} = 50 f3dB=50 kHz，PLL 环路带宽为 f l o o p = 500 f_{\mathrm{loop}} = 500 floop=500 kHz。与 OFDM 通信相反，OFDM 雷达中的 PN 统计特性取决于目标时延，这一点在图 1 中也进行了说明。

C. 与时延相关的 PN 协方差矩阵

令 w ≜ v e c ( W ) ∈ C N M × 1 \mathbf{w} \triangleq \mathrm{vec}(\mathbf{W}) \in \mathbb{C}^{NM \times 1} w≜vec(W)∈CNM×1 和 ξ ∈ R N M × 1 \boldsymbol{\xi} \in \mathbb{R}^{NM \times 1} ξ∈RNM×1 表示整个 OFDM 帧上 (15) 中 PN 过程的采样版本，即来自 (7) 的 w = e − j ξ \mathbf{w} = e^{-j\boldsymbol{\xi}} w=e−jξ。那么， ξ \boldsymbol{\xi} ξ 的统计特性可以描述为 6 ^6 6

6 ^6 6 按照引理 1 中的论证，通过计算与不同时延下不同目标相关的 PN 向量的互相关，可以将 PN 统计特性的推导直接扩展到多目标情况。

ξ ∼ N ( 0 , R ( τ ) ) , (20) \boldsymbol{\xi} \sim \mathcal{N}(\mathbf{0}, \mathbf{R}(\tau)), \tag{20} ξ∼N(0,R(τ)),(20)

其中 R ( τ ) ∈ R N M × N M \mathbf{R}(\tau) \in \mathbb{R}^{NM \times NM} R(τ)∈RNM×NM 是 ξ \boldsymbol{\xi} ξ 的与时延相关的正定协方差矩阵。利用 (16) 和 (17)， R ( τ ) \mathbf{R}(\tau) R(τ) 的第 ( i 1 , i 2 ) (i_1, i_2) (i1,i2) 个元素可以写为

R ( τ ) \] i 1 , i 2 = R ξ ξ ( Δ t i 1 i 2 , τ ) , (21) \[\\mathbf{R}(\\tau)\]_{i_1, i_2} = R_{\\xi\\xi}(\\Delta t_{i_1 i_2}, \\tau), \\tag{21} \[R(τ)\]i1,i2=Rξξ(Δti1i2,τ),(21) 其中 Δ t i 1 i 2 ≜ ( i 1 − i 2 ) T s + ( m 1 − m 2 ) T c p (22) \\Delta t_{i_1 i_2} \\triangleq (i_1 - i_2)T_s + (m_1 - m_2)T_{\\mathrm{cp}} \\tag{22} Δti1i2≜(i1−i2)Ts+(m1−m2)Tcp(22) 对于 ( i 1 , i 2 ) = ( n 1 + m 1 N , n 2 + m 2 N ) (i_1, i_2) = (n_1 + m_1 N, n_2 + m_2 N) (i1,i2)=(n1+m1N,n2+m2N)，其中 0 ≤ n 1 , n 2 ≤ N − 1 0 \\leq n_1, n_2 \\leq N - 1 0≤n1,n2≤N−1 和 0 ≤ m 1 , m 2 ≤ M − 1 0 \\leq m_1, m_2 \\leq M - 1 0≤m1,m2≤M−1 分别表示快时间和慢时间采样索引，且 T s = T / N T_s = T/N Ts=T/N 为采样间隔。我们从 (22) 注意到，由于 CP 的移除， Δ t i 1 i 2 \\Delta t_{i_1 i_2} Δti1i2 不仅取决于 i 1 − i 2 i_1 - i_2 i1−i2，还取决于属于不同符号的 PN 样本之间的符号（慢时间）索引差。 > 1. 变量定义回顾 > > * i i i (线性索引)：接收机得到的观测向量 Y \\mathbf{Y} Y 或 PN 向量 ξ \\boldsymbol{\\xi} ξ 中的第 i i i 个数据点。这个向量已经去除了 CP。 > * T s T_s Ts：采样间隔 ( T / N T/N T/N)。 T c p T_{\\mathrm{cp}} Tcp：循环前缀的持续时间。 > * 映射关系：任意线性索引 i i i 可以唯一映射到第 m m m 个符号的第 n n n 个采样点： i = m ⋅ N + n , 其中 0 ≤ n \< N i = m \\cdot N + n, \\quad \\text{其中 } 0 \\le n \< N i=m⋅N+n,其中 0≤n\ > 2. 物理时间的计算在物理世界中，振荡器是连续运行的。第 m m m 个符号的第 n n n 个有效数据采样点的绝对物理时间 t p h y s i c a l t_{physical} tphysical 是： t m , n = m ⋅ ( N T s + T c p ) ⏟ 前 m 个完整符号的时间 + T c p ⏟ 当前符号跳过的 CP + n ⋅ T s ⏟ 当前符号内的偏移 t_{m,n} = \\underbrace{m \\cdot (N T_s + T_{\\mathrm{cp}})}_{\\text{前 } m \\text{ 个完整符号的时间}} + \\underbrace{T_{\\mathrm{cp}}}_{\\text{当前符号跳过的 CP}} + \\underbrace{n \\cdot T_s}_{\\text{当前符号内的偏移}} tm,n=前 m 个完整符号的时间 m⋅(NTs+Tcp)+当前符号跳过的 CP Tcp+当前符号内的偏移 n⋅Ts注意：每个完整 OFDM 符号的物理长度是 T s y m = N T s + T c p T_{\\mathrm{sym}} = N T_s + T_{\\mathrm{cp}} Tsym=NTs+Tcp。我们在取第 n n n 个采样点时，已经在当前符号内跳过了 T c p T_{\\mathrm{cp}} Tcp 的时长。 > > 3. 计算时间差 Δ t \\Delta t Δt现在我们要计算两个索引 i 1 ( m 1 , n 1 ) i_1 (m_1, n_1) i1(m1,n1) 和 i 2 ( m 2 , n 2 ) i_2 (m_2, n_2) i2(m2,n2) 之间的物理时间差： Δ t = t m 1 , n 1 − t m 2 , n 2 \\Delta t = t_{m_1, n_1} - t_{m_2, n_2} Δt=tm1,n1−tm2,n2代入上面的物理时间公式： Δ t = \[ m 1 ( N T s + T c p ) + T c p + n 1 T s \] − \[ m 2 ( N T s + T c p ) + T c p + n 2 T s \] = ( m 1 − m 2 ) ( N T s + T c p ) + ( n 1 − n 2 ) T s + ( T c p − T c p ) ⏟ 0 \\begin{aligned} \\Delta t \&= \\left\[ m_1 (N T_s + T_{\\mathrm{cp}}) + T_{\\mathrm{cp}} + n_1 T_s \\right\] - \\left\[ m_2 (N T_s + T_{\\mathrm{cp}}) + T_{\\mathrm{cp}} + n_2 T_s \\right\] \\\\ \&= (m_1 - m_2)(N T_s + T_{\\mathrm{cp}}) + (n_1 - n_2) T_s + \\underbrace{(T_{\\mathrm{cp}} - T_{\\mathrm{cp}})}_{0} \\end{aligned} Δt=\[m1(NTs+Tcp)+Tcp+n1Ts\]−\[m2(NTs+Tcp)+Tcp+n2Ts\]=(m1−m2)(NTs+Tcp)+(n1−n2)Ts+0 (Tcp−Tcp)将 N T s N T_s NTs 和 T c p T_{\\mathrm{cp}} Tcp 的项分开整理： Δ t = ( m 1 − m 2 ) N T s + ( n 1 − n 2 ) T s + ( m 1 − m 2 ) T c p = \[ ( m 1 N + n 1 ) − ( m 2 N + n 2 ) \] ⏟ 这正是线性索引 i 1 − i 2 T s + ( m 1 − m 2 ) T c p \\begin{aligned} \\Delta t \&= (m_1 - m_2) N T_s + (n_1 - n_2) T_s + (m_1 - m_2) T_{\\mathrm{cp}} \\\\ \&= \\underbrace{\[ (m_1 N + n_1) - (m_2 N + n_2) \]}_{\\text{这正是线性索引 } i_1 - i_2} T_s + (m_1 - m_2) T_{\\mathrm{cp}} \\end{aligned} Δt=(m1−m2)NTs+(n1−n2)Ts+(m1−m2)Tcp=这正是线性索引 i1−i2 \[(m1N+n1)−(m2N+n2)\]Ts+(m1−m2)Tcp于是就得到了公式 (22)： Δ t i 1 i 2 = ( i 1 − i 2 ) T s + ( m 1 − m 2 ) T c p \\Delta t_{i_1 i_2} = (i_1 - i_2)T_s + (m_1 - m_2)T_{\\mathrm{cp}} Δti1i2=(i1−i2)Ts+(m1−m2)Tcp > > 4. 直观的物理图景你可以把这个公式看作两部分的叠加： > > * ( i 1 − i 2 ) T s (i_1 - i_2)T_s (i1−i2)Ts：这是假设没有 CP 时，两个采样点之间的时间差。因为 i 1 i_1 i1 和 i 2 i_2 i2 是数据向量中的紧密排列（没有空隙），所以它们直接对应了 T s T_s Ts 的倍数。 > * ( m 1 − m 2 ) T c p (m_1 - m_2)T_{\\mathrm{cp}} (m1−m2)Tcp：这是 **"丢失的时间"补偿项** 。 > * 如果我们比较的是同一个符号内的点（ m 1 = m 2 m_1 = m_2 m1=m2），这一项为 0。因为它们之间没有跨越 CP。 > * 如果我们比较的是相邻符号的点（ m 1 = m 2 + 1 m_1 = m_2 + 1 m1=m2+1），那么除了数据采样点的间隔外，物理振荡器还额外多跑了一段 T c p T_{\\mathrm{cp}} Tcp 的时间（即两个符号中间的那个 CP）。虽然数据里把这段 CP 扔了，但相位噪声在这段时间里依然在积累，所以计算相关性时必须把这段时间加回来。 从 (21) 和 (22) 可以直接看出， R ( τ ) \\mathbf{R}(\\tau) R(τ) 是一个对称的 Toeplitz-块 Toeplitz 矩阵（a symmetric Toeplitz-block Toeplitz matrix） \[64\]，由 M × M M \\times M M×M 个大小为 N × N N \\times N N×N 的块组成： R ( τ ) = \[ R 0 ( τ ) R 1 ( τ ) ⋯ R M − 1 ( τ ) R 1 T ( τ ) ⋱ ⋱ ⋮ ⋮ ⋱ ⋱ R 1 ( τ ) R M − 1 T ( τ ) ⋯ R 1 T ( τ ) R 0 ( τ ) \] , (23) \\mathbf{R}(\\tau) = \\begin{bmatrix} \\mathbf{R}_0(\\tau) \& \\mathbf{R}_1(\\tau) \& \\cdots \& \\mathbf{R}_{M-1}(\\tau) \\\\ \\mathbf{R}_1\^T(\\tau) \& \\ddots \& \\ddots \& \\vdots \\\\ \\vdots \& \\ddots \& \\ddots \& \\mathbf{R}_1(\\tau) \\\\ \\mathbf{R}_{M-1}\^T(\\tau) \& \\cdots \& \\mathbf{R}_1\^T(\\tau) \& \\mathbf{R}_0(\\tau) \\end{bmatrix}, \\tag{23} R(τ)= R0(τ)R1T(τ)⋮RM−1T(τ)R1(τ)⋱⋱⋯⋯⋱⋱R1T(τ)RM−1(τ)⋮R1(τ)R0(τ) ,(23) 其中第 m m m 个 Toeplitz 块 R m ( τ ) ∈ R N × N \\mathbf{R}_m(\\tau) \\in \\mathbb{R}\^{N \\times N} Rm(τ)∈RN×N 由下式给出 \[ R m ( τ ) \] n 1 , n 2 = R ξ ξ ( Δ t n 1 n 2 ( m ) , τ ) (24) \[\\mathbf{R}_m(\\tau)\]_{n_1, n_2} = R_{\\xi\\xi}(\\Delta t_{n_1 n_2}\^{(m)}, \\tau) \\tag{24} \[Rm(τ)\]n1,n2=Rξξ(Δtn1n2(m),τ)(24) 其中 Δ t n 1 n 2 ( m ) ≜ ( n 1 − n 2 ) T s − m T s y m \\Delta t_{n_1 n_2}\^{(m)} \\triangleq (n_1 - n_2)T_s - m T_{\\mathrm{sym}} Δtn1n2(m)≜(n1−n2)Ts−mTsym。虽然 PLL 表现出 (23) 中的通用 Toeplitz-块 Toeplitz 结构，但如下引理指出，FRO 会导致更特殊的协方差结构。 > *引理 2* ：对于 τ ≤ T c p \\tau \\leq T_{\\mathrm{cp}} τ≤Tcp 的 FRO，(23) 中的 PN 协方差矩阵 R ( τ ) \\mathbf{R}(\\tau) R(τ) 是块对角的，即 R ( τ ) = b l k d i a g ( R 0 ( τ ) , ... , R 0 ( τ ) ) . (25) \\mathbf{R}(\\tau) = \\mathrm{blkdiag}(\\mathbf{R}_0(\\tau), \\ldots, \\mathbf{R}_0(\\tau)). \\tag{25} R(τ)=blkdiag(R0(τ),...,R0(τ)).(25) > *证明*：请参阅补充材料中的 S-II 节。 引理 2 的一个直观解释如下（An intuitive interpretation of Lemma 2 can be provided as follows）。由于不同符号中的 PN 样本在时间上至少相隔 T c p T_{\\mathrm{cp}} Tcp，因此当 τ ≤ T c p \\tau \\leq T_{\\mathrm{cp}} τ≤Tcp 时，(15) 中的 PN 过程在不同符号之间变得不相关。 换句话说，对应于 ξ ( t , τ ) \\xi(t, \\tau) ξ(t,τ) 和 ξ ( t + T c p , τ ) \\xi(t + T_{\\mathrm{cp}}, \\tau) ξ(t+Tcp,τ) 的 PN 累积 \[48\] 时间间隔是不重叠的，这导致在没有控制环路的情况下 PN 不相关。图 2 也证实了这一结果，其中 FRO 的相关性在 Δ t ≥ τ \\Delta t \\geq \\tau Δt≥τ 时为零，而 PLL 的相关性在 Δ t ≥ T c p \\Delta t \\geq T_{\\mathrm{cp}} Δt≥Tcp 时可能具有非零值。 *备注 1*：本节提供的 PN 分析也可以应用于经典的单站雷达系统，例如 FMCW 和脉冲雷达。尽管 PN 协方差矩阵的结构可能会根据特定的波形属性而变化，但基本结果（即 PN 统计特性与时延相关）无论对于 OFDM、FMCW 还是脉冲雷达都是相同的。这是由单站雷达设置中 PN 过程的差分（自相关）性质决定的。因此，类似于本文提出的 PN 缓解和利用算法（即第四节中的算法 1 和第五节中的算法 2）也可以应用于 FMCW 和脉冲雷达系统。 ### IV. PROPOSED ALGORITHM FOR DELAY-DOPPLER ESTIMATION UNDER PHASE NOISE #### A. 混合 ML/MAP 估计器 > Y = α W ⊙ F N H ( X ⊙ b ( τ ) c H ( ν ) ) + Z (11) \\mathbf{Y} = \\alpha \\mathbf{W} \\odot \\mathbf{F}_N\^H \\left( \\mathbf{X} \\odot \\mathbf{b}(\\tau) \\mathbf{c}\^H(\\nu) \\right) + \\mathbf{Z} \\tag{11} Y=αW⊙FNH(X⊙b(τ)cH(ν))+Z(11) 为了推导时延、多普勒和 PN 的混合 ML/MAP 估计器，我们首先将 (11) 中的观测值重写为 y = α Ξ q ( τ , ν ) + z , (26) \\mathbf{y} = \\alpha \\mathbf{\\Xi} \\mathbf{q}(\\tau, \\nu) + \\mathbf{z}, \\tag{26} y=αΞq(τ,ν)+z,(26) 其中 y ≜ v e c ( Y ) ∈ C N M × 1 \\mathbf{y} \\triangleq \\mathrm{vec}(\\mathbf{Y}) \\in \\mathbb{C}\^{NM \\times 1} y≜vec(Y)∈CNM×1， z ≜ v e c ( Z ) ∈ C N M × 1 \\mathbf{z} \\triangleq \\mathrm{vec}(\\mathbf{Z}) \\in \\mathbb{C}\^{NM \\times 1} z≜vec(Z)∈CNM×1， Ξ ≜ d i a g ( e − j ξ ) ∈ C N M × N M , (27) \\mathbf{\\Xi} \\triangleq \\mathrm{diag} (e\^{-j\\boldsymbol{\\xi}}) \\in \\mathbb{C}\^{NM \\times NM}, \\tag{27} Ξ≜diag(e−jξ)∈CNM×NM,(27) q ( τ , ν ) ≜ v e c ( F N H \[ X ⊙ b ( τ ) c H ( ν ) \] ) ∈ C N M × 1 . (28) \\mathbf{q}(\\tau, \\nu) \\triangleq \\mathrm{vec} \\left( \\mathbf{F}_N\^H \[\\mathbf{X} \\odot \\mathbf{b}(\\tau)\\mathbf{c}\^H(\\nu)\] \\right) \\in \\mathbb{C}\^{NM \\times 1}. \\tag{28} q(τ,ν)≜vec(FNH\[X⊙b(τ)cH(ν)\])∈CNM×1.(28) 我们此处的目的是从 (26) 中估计未知参数向量 η = \[ τ , ν , α , ξ T \] T \\boldsymbol{\\eta} = \[\\tau, \\nu, \\alpha, \\boldsymbol{\\xi}\^T\]\^T η=\[τ,ν,α,ξT\]T，该向量由随机参数 ( ξ \\boldsymbol{\\xi} ξ) 和确定性参数 ( τ , ν , α \\tau, \\nu, \\alpha τ,ν,α) 组成 7 \^7 7。那么， η \\boldsymbol{\\eta} η 的混合 ML/MAP 估计器可以写为 \[53

7 ^7 7 由于 PN 的时变特性以及目标在时延-多普勒平面内可能的移动，对 η \boldsymbol{\eta} η 的估计需要在每个新的 OFDM 帧中进行。尽管 PN ξ \boldsymbol{\xi} ξ 具有 (20) 中指定的时不变统计特性，但它在每一帧中都有不同的（时变）实现，因此随着 (26) 形式的新观测值到来，需要通过重新执行第四节中提出的方法来进行重新估计。

( τ ^ , ν ^ , α ^ , ξ ^ ) = arg ⁡ max ⁡ τ , ν , α , ξ f y , ξ ( y , ξ ; τ , ν , α ) , (29) (\widehat{\tau}, \widehat{\nu}, \widehat{\alpha}, \widehat{\boldsymbol{\xi}}) = \arg \max_{\tau, \nu, \alpha, \boldsymbol{\xi}} f_{\mathbf{y}, \boldsymbol{\xi}}(\mathbf{y}, \boldsymbol{\xi}; \tau, \nu, \alpha), \tag{29} (τ ,ν ,α ,ξ )=argτ,ν,α,ξmaxfy,ξ(y,ξ;τ,ν,α),(29)

其中 f y , ξ ( y , ξ ; τ , ν , α ) f_{\mathbf{y}, \boldsymbol{\xi}}(\mathbf{y}, \boldsymbol{\xi}; \tau, \nu, \alpha) fy,ξ(y,ξ;τ,ν,α) 是 y \mathbf{y} y 和 ξ \boldsymbol{\xi} ξ 的联合概率密度函数 (PDF)，它是确定性参数 τ , ν \tau, \nu τ,ν 和 α \alpha α 的函数

f y , ξ ( y , ξ ; τ , ν , α ) = f y ∣ ξ ( y ∣ ξ ; τ , ν , α ) f ξ ( ξ ; τ ) , (30) f_{\mathbf{y}, \boldsymbol{\xi}}(\mathbf{y}, \boldsymbol{\xi}; \tau, \nu, \alpha) = f_{\mathbf{y}|\boldsymbol{\xi}}(\mathbf{y}|\boldsymbol{\xi}; \tau, \nu, \alpha) f_{\boldsymbol{\xi}}(\boldsymbol{\xi}; \tau), \tag{30} fy,ξ(y,ξ;τ,ν,α)=fy∣ξ(y∣ξ;τ,ν,α)fξ(ξ;τ),(30)

公式 (30) 的成立基于概率论中的链式法则 (Chain Rule) 以及物理模型中的条件独立性。

1. 联合概率的通用定义

根据贝叶斯定理，对于任意两个随机向量 y \mathbf{y} y 和 ξ \boldsymbol{\xi} ξ，其联合概率密度函数 (Joint PDF) 总是可以分解为"条件概率"乘以"边缘概率"： f A , B ( a , b ) = f A ∣ B ( a ∣ b ) ⋅ f B ( b ) f_{\mathbf{A}, \mathbf{B}}(\mathbf{a}, \mathbf{b}) = f_{\mathbf{A} | \mathbf{B}}(\mathbf{a} | \mathbf{b}) \cdot f_{\mathbf{B}}(\mathbf{b}) fA,B(a,b)=fA∣B(a∣b)⋅fB(b)
f y , ξ ( y , ξ ; Θ ) = f y ∣ ξ ( y ∣ ξ ; Θ ) ⋅ f ξ ( ξ ; Θ ) f_{\mathbf{y}, \boldsymbol{\xi}}(\mathbf{y}, \boldsymbol{\xi}; \Theta) = f_{\mathbf{y}|\boldsymbol{\xi}}(\mathbf{y}|\boldsymbol{\xi}; \Theta) \cdot f_{\boldsymbol{\xi}}(\boldsymbol{\xi}; \Theta) fy,ξ(y,ξ;Θ)=fy∣ξ(y∣ξ;Θ)⋅fξ(ξ;Θ)

其中 Θ = { τ , ν , α } \Theta = \{\tau, \nu, \alpha\} Θ={τ,ν,α} 为全套未知参数。代入后得到未化简形式：
f y , ξ ( y , ξ ; τ , ν , α ) = f y ∣ ξ ( y ∣ ξ ; τ , ν , α ) ⋅ f ξ ( ξ ; τ , ν , α ) f_{\mathbf{y}, \boldsymbol{\xi}}(\mathbf{y}, \boldsymbol{\xi}; \tau, \nu, \alpha) = f_{\mathbf{y}|\boldsymbol{\xi}}(\mathbf{y}|\boldsymbol{\xi}; \tau, \nu, \alpha) \cdot f_{\boldsymbol{\xi}}(\boldsymbol{\xi}; \tau, \nu, \alpha) fy,ξ(y,ξ;τ,ν,α)=fy∣ξ(y∣ξ;τ,ν,α)⋅fξ(ξ;τ,ν,α)

2. 基于物理模型的独立性化简

考察右侧第二项（相位噪声的先验分布）对参数的依赖性：

• 与 α , ν \alpha, \nu α,ν 独立 ：振荡器的物理噪声特性与目标的反射强度 ( α \alpha α) 和运动速度 ( ν \nu ν) 无关。
• 依赖于 τ \tau τ ：根据差分相位噪声模型，噪声的协方差矩阵 R ( τ ) \mathbf{R}(\tau) R(τ) 直接由目标时延 τ \tau τ 决定（距离相关效应）。

因此， ξ \boldsymbol{\xi} ξ 的分布仅由 τ \tau τ 参数化，先验概率项可化简为：
f ξ ( ξ ; τ , ν , α ) ⟶ f ξ ( ξ ; τ ) f_{\boldsymbol{\xi}}(\boldsymbol{\xi}; \tau, \nu, \alpha) \longrightarrow f_{\boldsymbol{\xi}}(\boldsymbol{\xi}; \tau) fξ(ξ;τ,ν,α)⟶fξ(ξ;τ)

3. 最终结果

将步骤 2 的化简结果代回步骤 1，即得公式 (30)：
f y , ξ ( y , ξ ; τ , ν , α ) = f y ∣ ξ ( y ∣ ξ ; τ , ν , α ) f ξ ( ξ ; τ ) (30) f_{\mathbf{y}, \boldsymbol{\xi}}(\mathbf{y}, \boldsymbol{\xi}; \tau, \nu, \alpha) = f_{\mathbf{y}|\boldsymbol{\xi}}(\mathbf{y}|\boldsymbol{\xi}; \tau, \nu, \alpha) f_{\boldsymbol{\xi}}(\boldsymbol{\xi}; \tau) \tag{30} fy,ξ(y,ξ;τ,ν,α)=fy∣ξ(y∣ξ;τ,ν,α)fξ(ξ;τ)(30)

f y ∣ ξ ( y ∣ ξ ; τ , ν , α ) f_{\mathbf{y}|\boldsymbol{\xi}}(\mathbf{y}|\boldsymbol{\xi}; \tau, \nu, \alpha) fy∣ξ(y∣ξ;τ,ν,α) 是给定 ξ \boldsymbol{\xi} ξ 时 y \mathbf{y} y 的条件 PDF，而 f ξ ( ξ ; τ ) f_{\boldsymbol{\xi}}(\boldsymbol{\xi}; \tau) fξ(ξ;τ) 是 ξ \boldsymbol{\xi} ξ 的先验 PDF。由 (20) 和 (26) 可得

f y ∣ ξ ( y ∣ ξ ; τ , ν , α ) = 1 ( 2 π σ 2 ) N M exp ⁡ { − ∥ y − α Ξ q ( τ , ν ) ∥ 2 2 σ 2 } , (31) f_{\mathbf{y}|\boldsymbol{\xi}}(\mathbf{y}|\boldsymbol{\xi}; \tau, \nu, \alpha) = \frac{1}{(2\pi\sigma^2)^{NM}} \exp \left\{ - \frac{\|\mathbf{y} - \alpha \mathbf{\Xi} \mathbf{q}(\tau, \nu)\|^2}{2\sigma^2} \right\}, \tag{31} fy∣ξ(y∣ξ;τ,ν,α)=(2πσ2)NM1exp{−2σ2∥y−αΞq(τ,ν)∥2},(31)

f ξ ( ξ ; τ ) = 1 ( 2 π ) N M det ⁡ ( R ( τ ) ) exp ⁡ { − ξ T R ( τ ) − 1 ξ 2 } . (32) f_{\boldsymbol{\xi}}(\boldsymbol{\xi}; \tau) = \frac{1}{\sqrt{(2\pi)^{NM} \det(\mathbf{R}(\tau))}} \exp \left\{ - \frac{\boldsymbol{\xi}^T \mathbf{R}(\tau)^{-1} \boldsymbol{\xi}}{2} \right\}. \tag{32} fξ(ξ;τ)=(2π)NMdet(R(τ)) 1exp{−2ξTR(τ)−1ξ}.(32)

将 (30)--(32) 代入 (29) 可得

( τ ^ , ν ^ , α ^ , ξ ^ ) = arg ⁡ min ⁡ τ , ν , α , ξ { ∥ y − α Ξ q ( τ , ν ) ∥ 2 2 σ 2 + ξ T R ( τ ) − 1 ξ + log ⁡ det ⁡ R ( τ ) 2 } . (33) \begin{aligned} (\widehat{\tau}, \widehat{\nu}, \widehat{\alpha}, \widehat{\boldsymbol{\xi}}) &= \arg \min_{\tau, \nu, \alpha, \boldsymbol{\xi}} \left\{ \frac{\|\mathbf{y} - \alpha \mathbf{\Xi} \mathbf{q}(\tau, \nu)\|^2}{2\sigma^2} \right. \\ &\left. + \frac{\boldsymbol{\xi}^T \mathbf{R}(\tau)^{-1} \boldsymbol{\xi} + \log \det \mathbf{R}(\tau)}{2} \right\}. \end{aligned} \tag{33} (τ ,ν ,α ,ξ )=argτ,ν,α,ξmin{2σ2∥y−αΞq(τ,ν)∥2+2ξTR(τ)−1ξ+logdetR(τ)}.(33)

对于给定的 τ , ν \tau, \nu τ,ν 和 ξ \boldsymbol{\xi} ξ，(33) 中 α \alpha α 的最优估计由下式给出

α ^ = q H ( τ , ν ) Ξ H y q H ( τ , ν ) Ξ H Ξ q ( τ , ν ) = q H ( τ , ν ) Ξ H y ∥ X ∥ F 2 , (34) \widehat{\alpha} = \frac{\mathbf{q}^H(\tau, \nu)\mathbf{\Xi}^H \mathbf{y}}{\mathbf{q}^H(\tau, \nu)\mathbf{\Xi}^H \mathbf{\Xi} \mathbf{q}(\tau, \nu)} = \frac{\mathbf{q}^H(\tau, \nu)\mathbf{\Xi}^H \mathbf{y}}{\|\mathbf{X}\|_F^2}, \tag{34} α =qH(τ,ν)ΞHΞq(τ,ν)qH(τ,ν)ΞHy=∥X∥F2qH(τ,ν)ΞHy,(34)

其中最后一个等式源自 (9), (10) 和 (28)：

∥ q ( τ , ν ) ∥ 2 = ∥ F N H ( X ⊙ b ( τ ) c H ( ν ) ) ∥ F 2 = ∥ X ⊙ b ( τ ) c H ( ν ) ∥ F 2 = ∥ X ∥ F 2 . (35) \begin{aligned} \|\mathbf{q}(\tau, \nu)\|^2 &= \|\mathbf{F}_N^H (\mathbf{X} \odot \mathbf{b}(\tau)\mathbf{c}^H(\nu))\|_F^2 \\ &= \|\mathbf{X} \odot \mathbf{b}(\tau)\mathbf{c}^H(\nu)\|_F^2 = \|\mathbf{X}\|_F^2. \end{aligned} \tag{35} ∥q(τ,ν)∥2=∥FNH(X⊙b(τ)cH(ν))∥F2=∥X⊙b(τ)cH(ν)∥F2=∥X∥F2.(35)

将 (34) 代入 (33)，混合 ML/MAP 问题变为

( τ ^ , ν ^ , ξ ^ ) = arg ⁡ min ⁡ τ , ν , ξ y H Π Ξ q ( τ , ν ) ⊥ y σ 2 + ξ T R ( τ ) − 1 ξ + log ⁡ det ⁡ R ( τ ) , (36) \begin{aligned} (\widehat{\tau}, \widehat{\nu}, \widehat{\boldsymbol{\xi}}) &= \arg \min_{\tau, \nu, \boldsymbol{\xi}} \frac{\mathbf{y}^H \mathbf{\Pi}_{\mathbf{\Xi}\mathbf{q}(\tau, \nu)}^{\perp} \mathbf{y}}{\sigma^2} + \boldsymbol{\xi}^T \mathbf{R}(\tau)^{-1} \boldsymbol{\xi} \\ &+ \log \det \mathbf{R}(\tau), \end{aligned} \tag{36} (τ ,ν ,ξ )=argτ,ν,ξminσ2yHΠΞq(τ,ν)⊥y+ξTR(τ)−1ξ+logdetR(τ),(36)

其中

Π Ξ q ( τ , ν ) ⊥ = I − Ξ q ( τ , ν ) q H ( τ , ν ) Ξ H ∥ q ( τ , ν ) ∥ 2 = Ξ Ξ H − Ξ q ( τ , ν ) q H ( τ , ν ) Ξ H ∥ q ( τ , ν ) ∥ 2 = Ξ ( I − q ( τ , ν ) q H ( τ , ν ) ∥ q ( τ , ν ) ∥ 2 ) Ξ H = Ξ Π q ( τ , ν ) ⊥ Ξ H , (37) \begin{aligned} \mathbf{\Pi}{\mathbf{\Xi}\mathbf{q}(\tau, \nu)}^{\perp} &= \mathbf{I} - \frac{\mathbf{\Xi}\mathbf{q}(\tau, \nu)\mathbf{q}^H(\tau, \nu)\mathbf{\Xi}^H}{\|\mathbf{q}(\tau, \nu)\|^2} \\ &= \mathbf{\Xi}\mathbf{\Xi}^H - \frac{\mathbf{\Xi}\mathbf{q}(\tau, \nu)\mathbf{q}^H(\tau, \nu)\mathbf{\Xi}^H}{\|\mathbf{q}(\tau, \nu)\|^2} \\ &= \mathbf{\Xi} \left( \mathbf{I} - \frac{\mathbf{q}(\tau, \nu)\mathbf{q}^H(\tau, \nu)}{\|\mathbf{q}(\tau, \nu)\|^2} \right) \mathbf{\Xi}^H \\ &= \mathbf{\Xi} \mathbf{\Pi}{\mathbf{q}(\tau, \nu)}^{\perp} \mathbf{\Xi}^H, \end{aligned} \tag{37} ΠΞq(τ,ν)⊥=I−∥q(τ,ν)∥2Ξq(τ,ν)qH(τ,ν)ΞH=ΞΞH−∥q(τ,ν)∥2Ξq(τ,ν)qH(τ,ν)ΞH=Ξ(I−∥q(τ,ν)∥2q(τ,ν)qH(τ,ν))ΞH=ΞΠq(τ,ν)⊥ΞH,(37)

其中 Ξ Ξ H = I \mathbf{\Xi}\mathbf{\Xi}^H = \mathbf{I} ΞΞH=I 源自 (27)。将 (37) 代入 (36)，我们得到

( τ ^ , ν ^ , ξ ^ ) = arg ⁡ min ⁡ τ , ν , ξ L ( τ , ν , ξ ) , (38) (\widehat{\tau}, \widehat{\nu}, \widehat{\boldsymbol{\xi}}) = \arg \min_{\tau, \nu, \boldsymbol{\xi}} \mathcal{L}(\tau, \nu, \boldsymbol{\xi}), \tag{38} (τ ,ν ,ξ )=argτ,ν,ξminL(τ,ν,ξ),(38)

其中

L ( τ , ν , ξ ) = y H Ξ Π q ( τ , ν ) ⊥ Ξ H y σ 2 + ξ T R ( τ ) − 1 ξ + log ⁡ det ⁡ R ( τ ) . (39) \begin{aligned} \mathcal{L}(\tau, \nu, \boldsymbol{\xi}) &= \frac{\mathbf{y}^H \mathbf{\Xi} \mathbf{\Pi}_{\mathbf{q}(\tau, \nu)}^{\perp} \mathbf{\Xi}^H \mathbf{y}}{\sigma^2} + \boldsymbol{\xi}^T \mathbf{R}(\tau)^{-1} \boldsymbol{\xi} \\ &+ \log \det \mathbf{R}(\tau). \end{aligned} \tag{39} L(τ,ν,ξ)=σ2yHΞΠq(τ,ν)⊥ΞHy+ξTR(τ)−1ξ+logdetR(τ).(39)