多元函数的神经网络与深度学习

多元函数的神经网络与深度学习是一种强大的数学方法，它可以用于解决各种复杂的问题。

1.1 概念

**神经网络：**神经网络是由多个节点(神经元)和连接这些节点的权重组成的。每个节点接收输入，进行计算，并输出结果。神经网络可以分为多层，每层之间通过权重连接。
**激活函数：**激活函数是用于对神经元输出结果进行非线性处理的函数。常见的激活函数有sigmoid、ReLU和tanh等。
**损失函数：**损失函数用于衡量模型预测结果与真实结果之间的差异。常见的损失函数有均方误差(MSE)、交叉熵损失(cross-entropy loss)等。
**梯度下降：**梯度下降是用于优化神经网络中权重参数的算法。通过不断更新权重参数，使损失函数值逐渐减小，从而使模型预测结果更接近真实结果。
**反向传播：**反向传播是用于计算梯度下降算法中梯度的算法。通过从输出层向输入层传播，计算每个权重参数的梯度。
**深度学习：**深度学习是一种使用多层神经网络进行自动学习的方法。通过大量数据的训练，深度学习模型可以自动学习出复杂问题的解决方案。

2.1 神经网络

神经网络是一种模拟人类大脑工作方式的计算模型。它由多个节点(神经元)和连接这些节点的权重组成。每个节点接收输入，进行计算，并输出结果。神经网络可以分为多层，每层之间通过权重连接。

2.1.1 神经元

神经元是神经网络的基本单元，它接收输入信号，进行处理，并输出结果。神经元可以分为两类：

**人工神经元：**人工神经元接收多个输入信号，通过一个激活函数进行处理，并输出一个输出信号。人工神经元可以具有多个输入和多个输出。
**模拟神经元：**模拟神经元模拟了生物神经元的工作方式。它接收多个输入信号，通过一个阈值函数进行处理，并输出一个输出信号。模拟神经元只具有一个输入和一个输出。

2.1.2 权重

权重是神经网络中连接不同节点的线路的强度。权重可以通过训练来调整，以使模型更好地适应数据。权重可以是正数、负数或零。

2.1.3 激活函数

激活函数是用于对神经元输出结果进行非线性处理的函数。常见的激活函数有sigmoid、tanh和ReLU等。激活函数可以帮助神经网络学习更复杂的模式，并避免过拟合。

2.1.4 损失函数

损失函数用于衡量模型预测结果与真实结果之间的差异。常见的损失函数有均方误差(MSE)、交叉熵损失(cross-entropy loss)等。损失函数可以帮助神经网络学习如何最小化预测错误。

2.1.5 梯度下降

梯度下降是用于优化神经网络中权重参数的算法。通过不断更新权重参数，使损失函数值逐渐减小，从而使模型预测结果更接近真实结果。梯度下降算法可以帮助神经网络学习如何最小化预测错误。

2.1.6 反向传播

反向传播是用于计算梯度下降算法中梯度的算法。通过从输出层向输入层传播，计算每个权重参数的梯度。反向传播算法可以帮助神经网络学习如何最小化预测错误。

2.2 深度学习

深度学习是一种使用多层神经网络进行自动学习的方法。通过大量数据的训练，深度学习模型可以自动学习出复杂问题的解决方案。

2.2.1 多层神经网络

多层神经网络是一种具有多个隐藏层的神经网络。每个隐藏层之间通过权重连接，形成一种层次结构。多层神经网络可以处理更复杂的问题，并具有更强的泛化能力。

3.核心算法

3.1 神经网络的前向传播

神经网络的前向传播是指从输入层到输出层的信息传播过程。具体操作步骤如下：

将输入数据输入到输入层。
在每个隐藏层中，对输入数据进行权重乘以和偏置求和，然后通过激活函数进行非线性处理。
重复步骤2，直到输出层。
从输出层获取最终预测结果。

3.2 神经网络的反向传播

神经网络的反向传播是指从输出层到输入层的梯度计算过程。具体操作步骤如下：

在输出层，计算损失函数值。
在每个隐藏层中，计算梯度，并通过链Rule求导，得到每个权重和偏置的梯度。
重复步骤2，直到输入层。
更新权重和偏置，使损失函数值逐渐减小。

3.3 梯度下降算法

梯度下降算法是一种优化神经网络中权重参数的方法。具体操作步骤如下：

初始化权重参数。
计算损失函数值。
使用反向传播计算梯度。
更新权重参数，使损失函数值逐渐减小。
重复步骤2-4，直到收敛。

深度学习与机器学习的区别

深度学习是一种机器学习方法，它使用多层神经网络进行自动学习。机器学习是一种计算机科学的分支，它涉及到算法的开发和应用，以便让计算机从数据中学习出模式。深度学习是机器学习的一个子集，它专注于使用多层神经网络进行自动学习。

深度学习与人工智能的区别

深度学习是一种人工智能技术，它旨在模拟人类大脑的工作方式。人工智能是一种计算机科学的分支，它涉及到创建智能体，以便让计算机进行自主决策和行动。深度学习是人工智能的一个子集，它专注于使用多层神经网络模拟人类大脑的工作方式。

主流的深度学习框架有以下几个：

TensorFlow：开发于Google的开源深度学习框架，支持多种编程语言，如Python、C++和Go。

PyTorch：开发于Facebook的开源深度学习框架，支持动态计算图和张量操作，具有高度灵活性。

Keras：开发于Google的开源深度学习框架，支持Python编程语言，具有简单易用的API。

Caffe：开发于Berkeley的开源深度学习框架，支持多种编程语言，如C++和Python。

Theano：开发于University of Montreal的开源深度学习框架，支持Python编程语言，具有高效的数值计算能力。

4 多层神经网络

4.1 线性函数与多层神经元的关系

核心关系：多层神经元的组合是为了克服单层线性模型的根本局限

线性函数的局限（单层网络）：

无论你怎么组合输入，单层线性模型（没有非线性激活）只能解决线性可分的问题（比如用一条直线/平面将数据分类）。
它无法解决像"异或"这样简单的非线性可分问题。

多层神经元的威力（引入非线性）：

每一层神经元都先进行线性变换，然后施加非线性激活。
这些非线性变换被逐层复合 。这种复合不是简单的线性叠加，而是产生了非线性的函数嵌套。
关键点 ：这种嵌套的非线性结构，使得网络能够拟合任意复杂的非线性函数。

直观类比：用乐高积木搭建复杂形状

线性函数 好比是标准的基础积木块（长方体）。只用基础块，你很难搭建出曲线、弧面等复杂结构。

非线性激活函数 好比是各种特殊形状的积木（弯的、带弧度的、三角形的）。

多层神经元 就是将这些特殊积木一层层组合起来的过程。通过组合，你可以逼近任何你想要的复杂形状（函数）。

4.2 人类大脑神经与神经元

4.3 神经元与矩阵

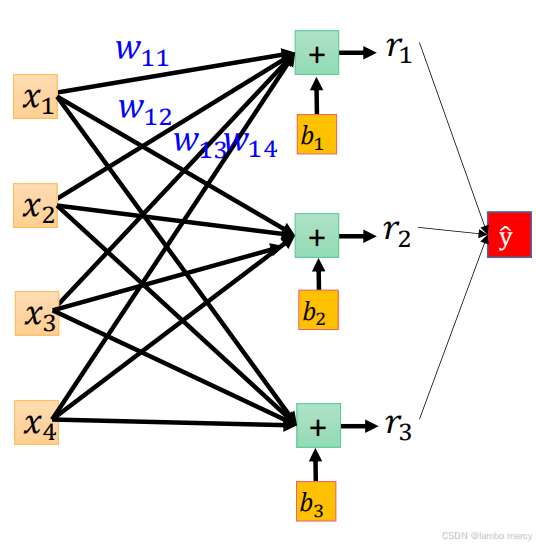
上面是一个神经网络结构示意图，

输入层：包含 4 个输入节点（x1,x2,x3,x4），用于接收原始数据；
隐藏层：包含 3 个节点（r1,r2,r3），每个节点通过权重（w11,w12,...）与输入层全连接，节点内的 "+" 代表加权求和操作，b1,b2,b3为偏置项；
输出层：包含 1 个输出节点（y^），通过权重（c1,c2,c3）与隐藏层全连接，最终输出预测结果，b为输出层偏置。

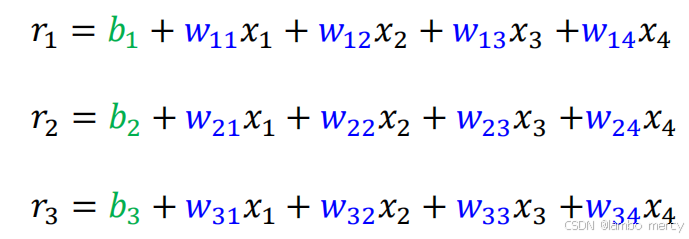
我们可以轻松的算出隐藏层r1,r2,r3的值，有没有觉得很眼熟，这就是矩阵相乘相加嘛

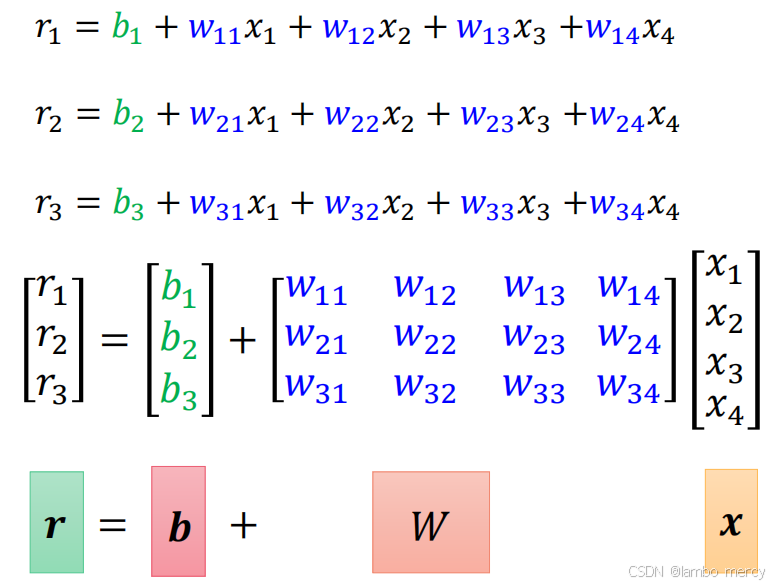
同理，求y也是矩阵相乘

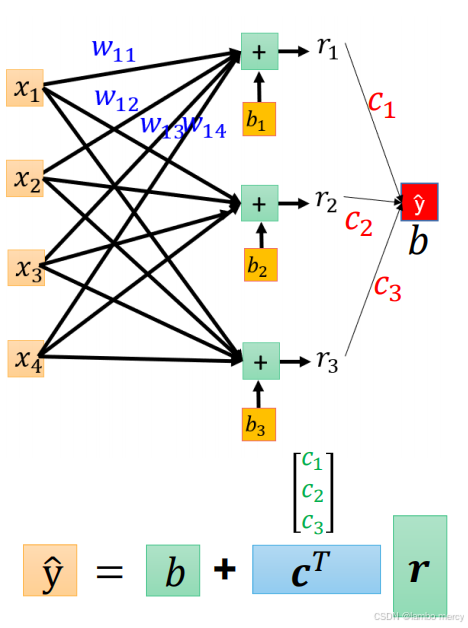
4.4串联的神经元

如何理解下面这句话：
串联的神经元似乎只有传递的作用，那么一根和多根似乎没有区别。

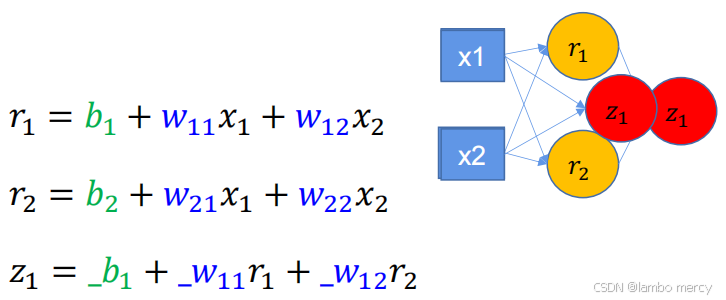
串联的神经元，无论多深都会回归到一层

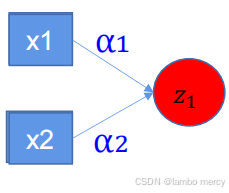
这时候我们就引入了激活函数

4.5 激活函数

生物神经元具有兴奋和抑制两种状态，当接受的刺激高于一定阈值时，则会进入兴奋状态并将神经冲动由轴突传出，反之则没有神经冲动。
什么意思？好比冬天的教室，呆在屋子里的同学不觉得臭，而从外面走进来的老师觉得很臭，这是因为同学长期在一个臭的环境中，他对臭味的阈值拉高了，臭味没有超过阈值，生物神经元就不往后传递，不需要通知大脑这是一个臭的环境，而老师从外面走进来，他的阈值是比较低的，教室里的臭味超过了这个阈值，生物神经元通过传递通知大脑，臭了臭了！

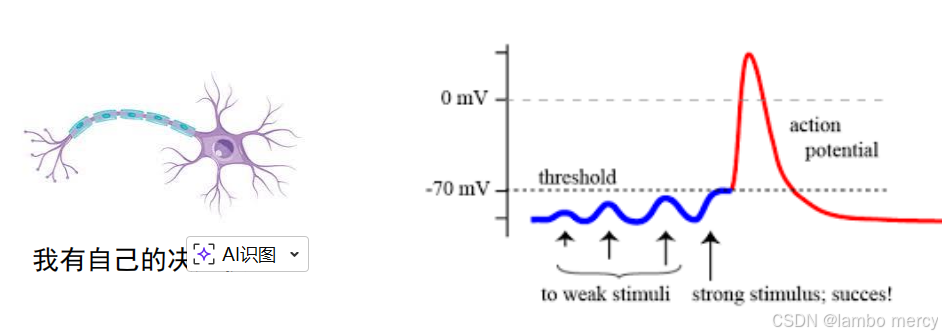
那大脑神经中有刺激阈值，那么计算机中也有所谓的激活函数：大脑神经中的刺激阈值作用在两个生物神经元中间，超过就传递。而计算机中的神经元也是作用在节点和节点之间的，有两种状态分别是抑制状态和激活状态。

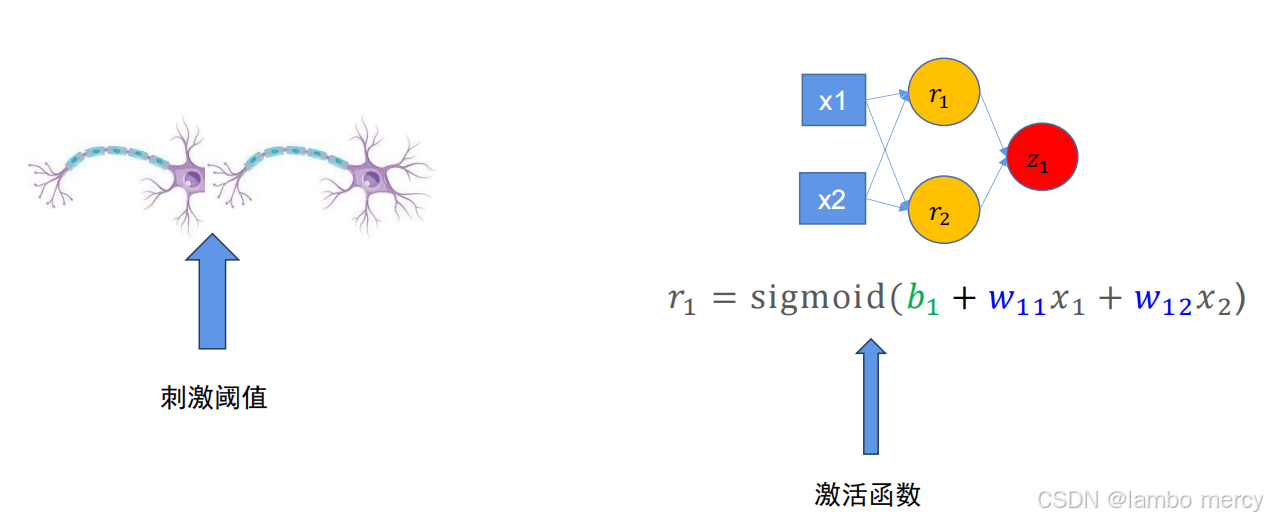
激活函数和非线性因素。

如果没有激活函数，无论网络多么复杂，最后的输出都是输入的线性组合，而纯粹的线性组合并，不能解决更为复杂的问题。

引入激活函数之后，由于激活函数都是非线性的 ，这样就给神经元引入了非线性元素，使得神经网络可以逼近任何非线性函数，这样使得神经网络应用到更多非线性模型中。

4.5.1 sigmoid

Sigmoid 函数也称为 Logistic 函数，是一种常用的激活函数，它将输入值压缩到 (0, 1) 区间内，表达式为

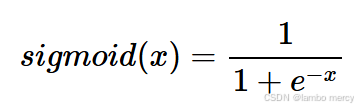
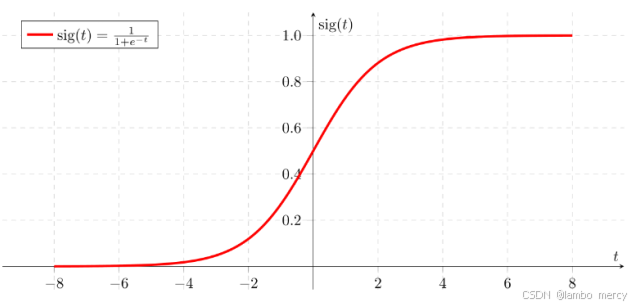
Sigmoid 函数的图像是一条平滑的 S 形曲线，当 x 趋近于负无穷时，函数值趋近于 0；当 x 趋近于正无穷时，函数值趋近于 1。在 x=0 处，函数值是 0.5 。

优点
1、输出范围固定 ：输出值在 (0, 1) 之间，适合用于二分类问题的输出层，可将输出解释为概率。
2、平滑可导 **：**函数处处连续可导，便于使用梯度下降等基于梯度的优化算法进行参数更新。

缺点
1、梯度消失问题 ：在 x 绝对值较大时，函数的梯度趋近于 0，导致在反向传播过程中，梯度很难传递到前面的层，使得网络难以训练，即出现梯度消失现象。
2、非零均值输出 ：输出值恒大于 0，这会导致后一层神经元的输入是非零均值的信号，可能会使梯度更新出现偏移，影响训练效果。
3、计算复杂度较高 **：**涉及指数运算，在计算资源有限或大规模网络中，计算效率相对较低。

4.5.2 ReLU

ReLU（Rectified Linear Unit，修正线性单元）函数是目前神经网络中使用最为广泛的激活函数之一，表达式为

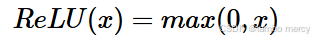
即当x≥0时，函数值为x；当x<0时，函数值为0。

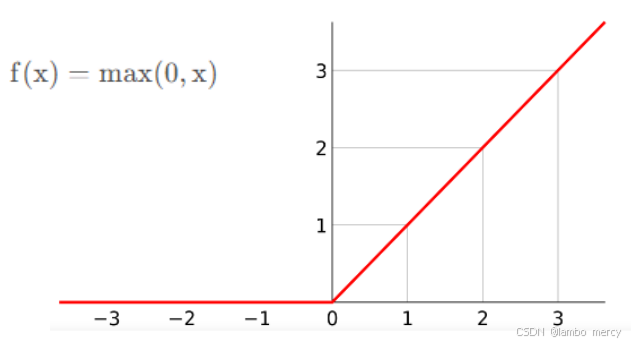
激活函数最重要的特性：能求导！

4.5.3 激活函数的位置

激活函数的位置紧接在线性变换（加权求和）之后。

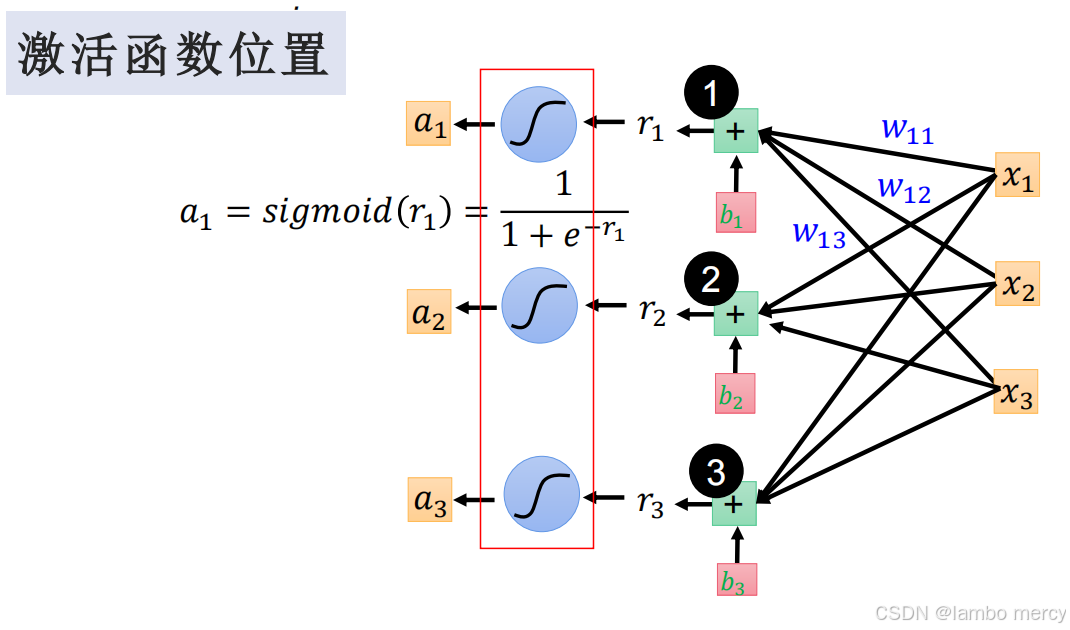
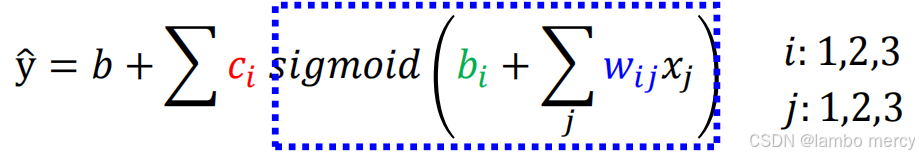
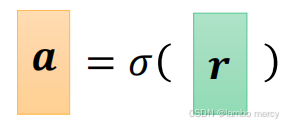
4.5.4 激活函数的效果

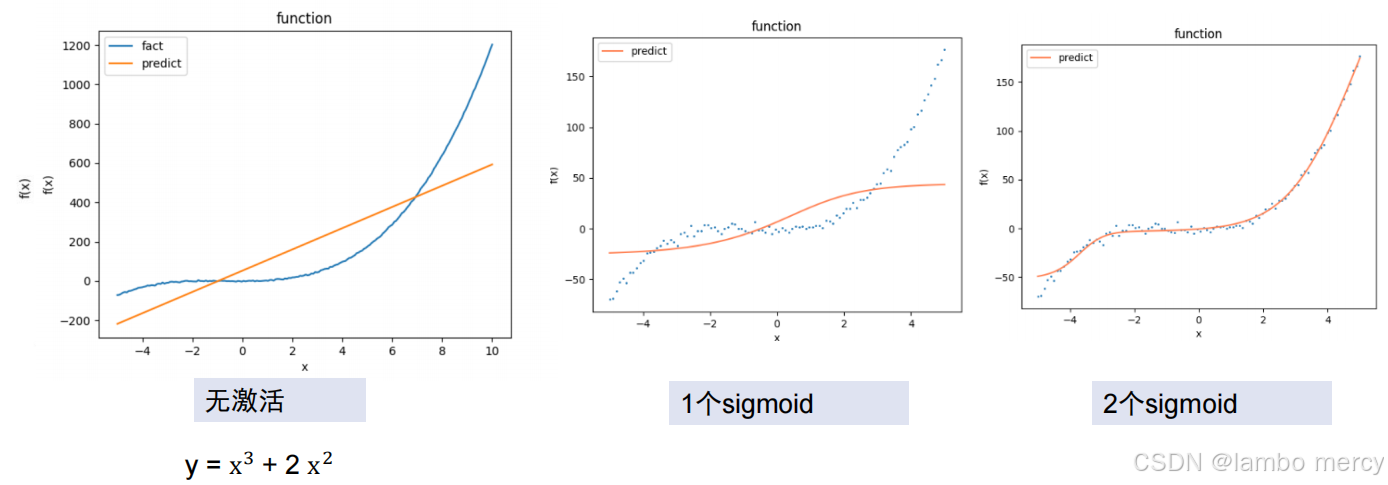
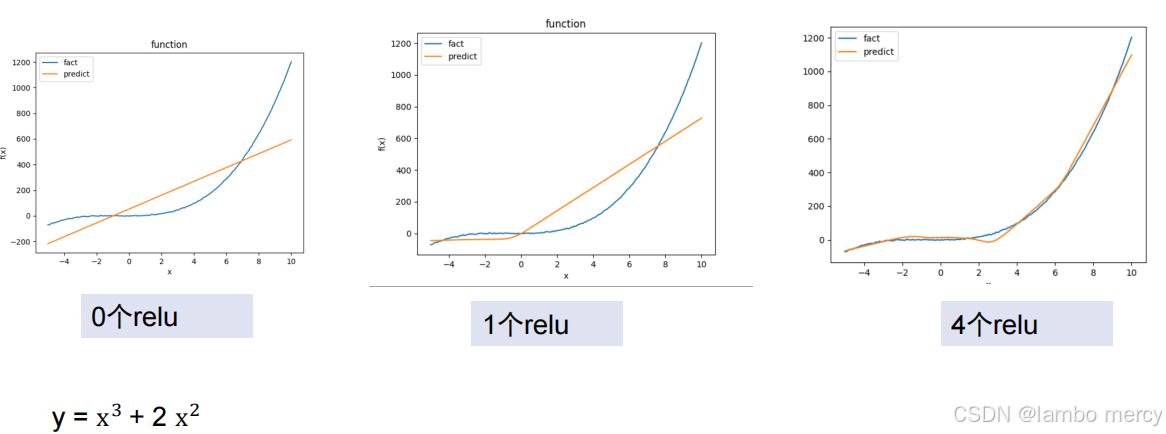
4.6 拟合和激活函数

激活函数是神经网络获得强大非线性拟合能力的"引擎"，没有它，网络无论多深都只能拟合线性关系。

线性模型的局限：无论堆多少层，都是线性变换的复合，结果仍是线性的

激活函数可以在线性变换之间插入非线性扭曲：

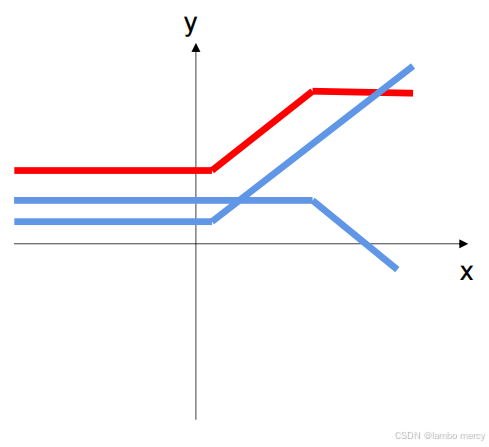
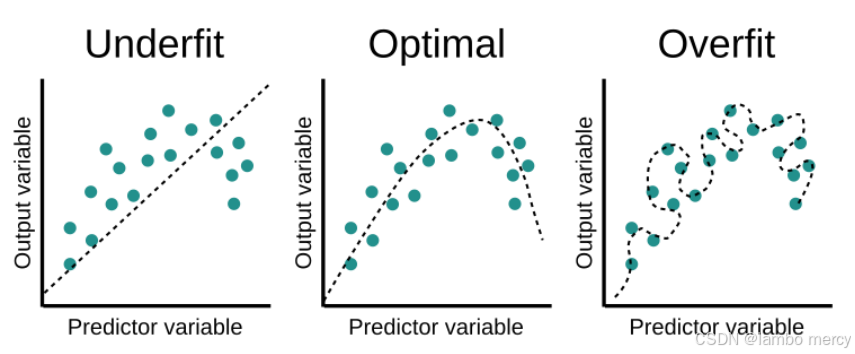
过拟合与欠拟合(左1欠拟合，左3过拟合 )

看图就很好理解

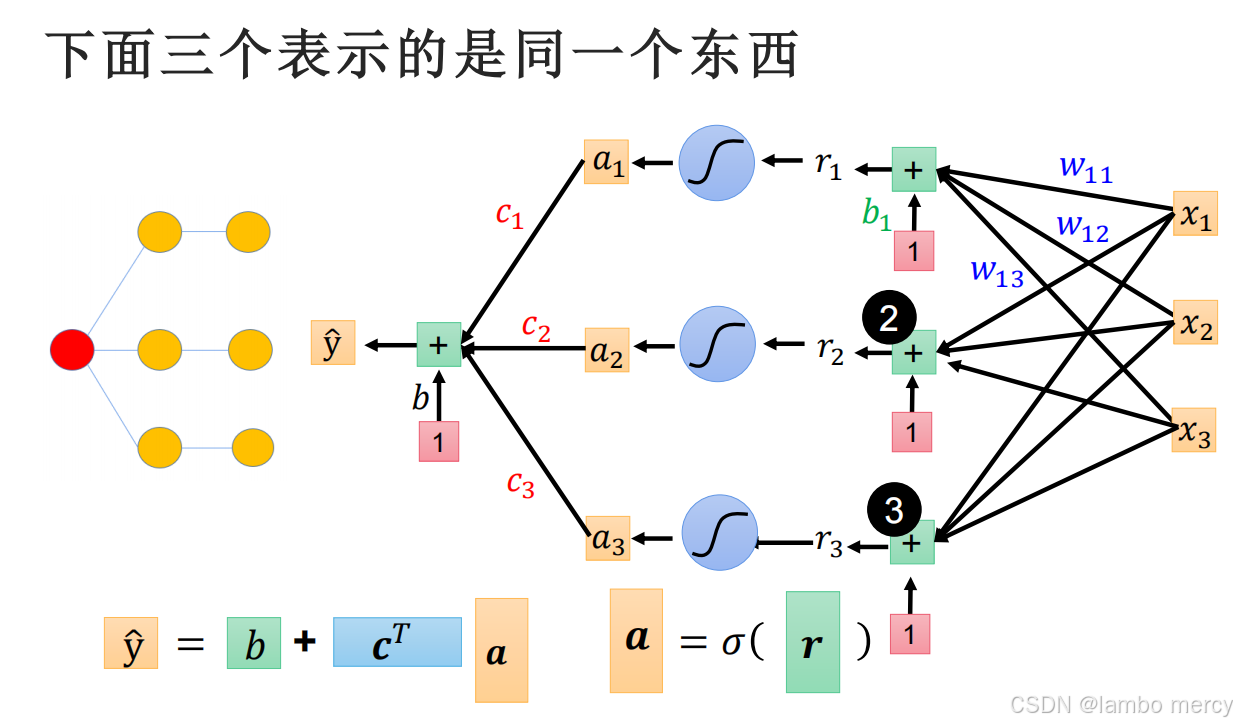
4.7 神经网络的参数

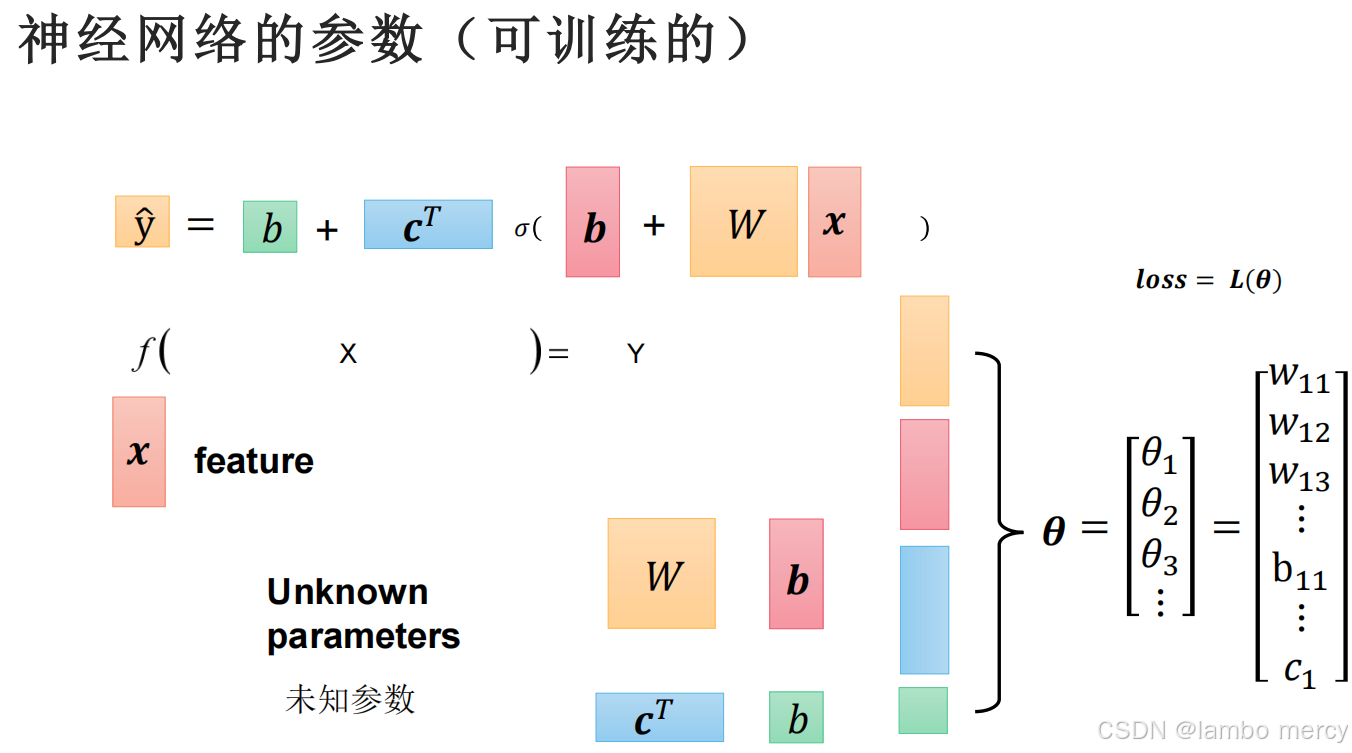
在上面这个例子中，未知参数w有9个，b有3+1个，c有3个

4.8 深度学习的训练过程

其实跟线性的训练过程一样，先前进，后梯度回传，

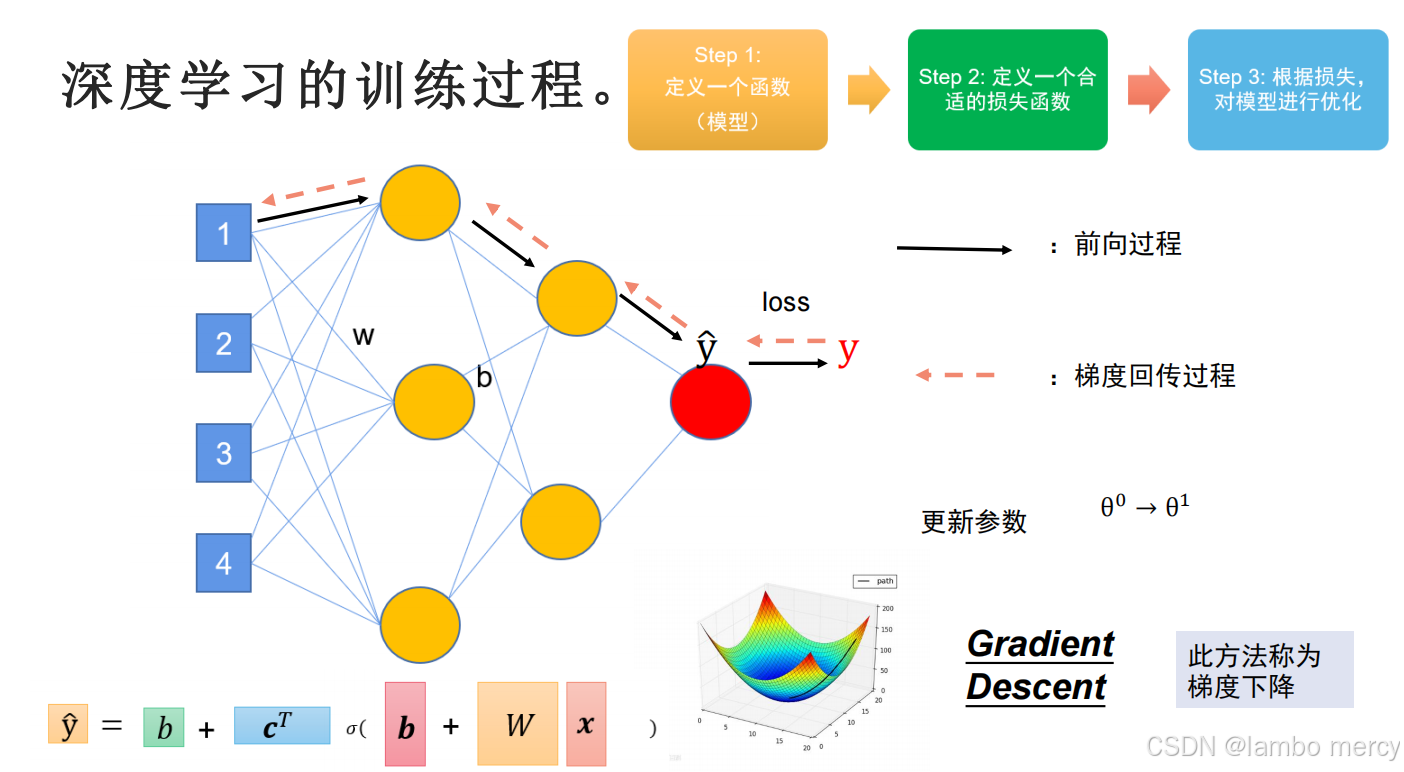
只不过计算量会变得很大：

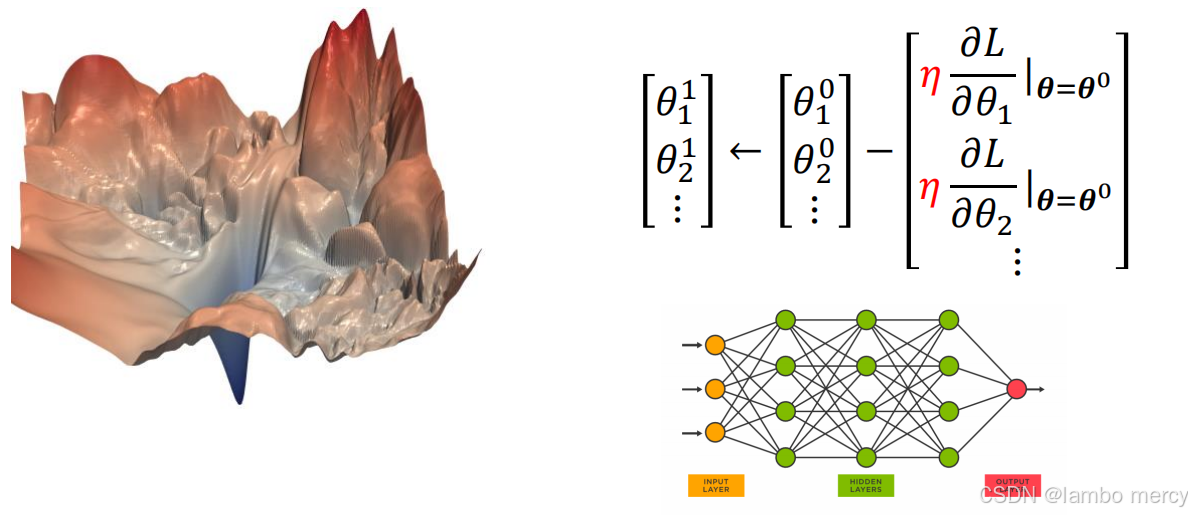
但是没关系，不需要我们去算，只需要丢给黑匣子，让计算机去算就行了

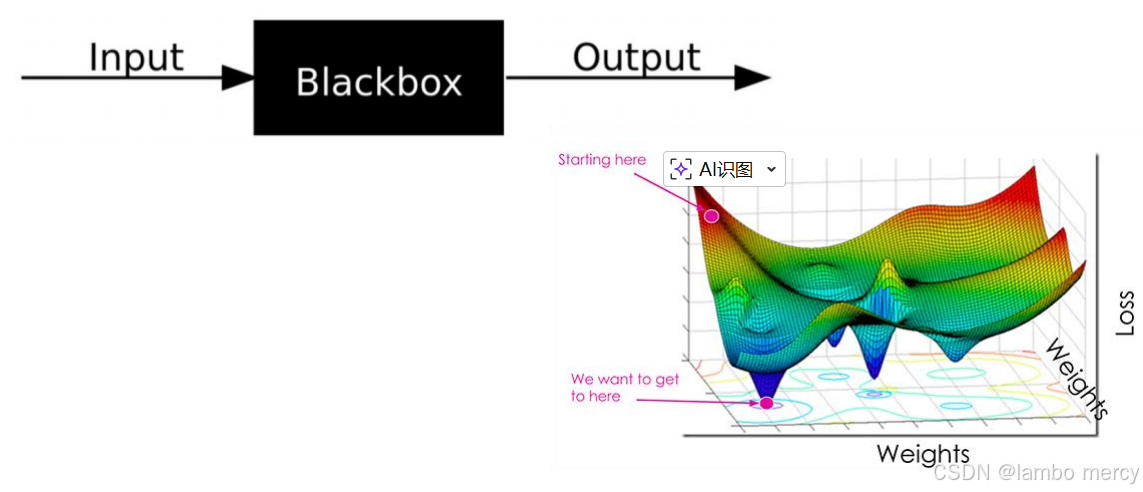
原先深度学习还不叫deep learning,而是叫Neural Network

但是受限于当时的显卡性能不好，出来的结果准确性比较差，在学术界没有得到认可，后来显卡好起来了，大家又开始发论文，想了一个新的名字就叫做deep learning。

我们上面提到的模型也叫做多层感知机。

现在的deep深度到底有多深？

Deep LearningarningDeep LearningDeDeep LearningDeep Learningep Learning

5 神经网络透析

5.1

函数的结构= 模型的架构
个人经验（玄学）
●神经网络，可以完成超级复杂的任务。诸如图片生成，人脸识别等等。
●但回归到一些原始纯粹的简单问题上，它表现得可能没那么好。如：判断一个数字是否为偶数。这些都需要先验知识
神经网络就像一个小婴儿，他会看会识别人脸，但不会完成需要先验知识的任务