数据结构 -- 常见的八大排序算法

不会c嘎嘎2026-01-03 11:37

目录

前言

[1. 插入排序](#1. 插入排序)

[1.1 直接插入排序](#1.1 直接插入排序)

[1.2 希尔排序](#1.2 希尔排序)

[2. 选择排序](#2. 选择排序)

[2.1 选择排序--双向优化版](#2.1 选择排序--双向优化版)

[2.2 堆排序](#2.2 堆排序)

[3. 交换排序](#3. 交换排序)

[3.1 冒泡排序](#3.1 冒泡排序)

[3.2 快速排序 - Hoare 版本](#3.2 快速排序 - Hoare 版本)

[3.2.1核心难点：为什么必须让 Right (右指针) 先走？](#3.2.1核心难点：为什么必须让 Right (右指针) 先走？)

3.2.2优化方案

[3.3 非递归快排](#3.3 非递归快排)

[4. 归并排序](#4. 归并排序)

[4.1 递归版 - 归并排序](#4.1 递归版 - 归并排序)

[4.2 非递归版 - 归并排序](#4.2 非递归版 - 归并排序)

[5. 非交换排序](#5. 非交换排序)

[5.1 计数排序](#5.1 计数排序)

[6. 总结](#6. 总结)

前言

著名的计算机科学家 Niklaus Wirth 曾说过："程序 = 数据结构 + 算法"。如果说数据结构是编程的地基，那么排序算法就是构建高楼大厦的第一块砖。

在日常开发中，我们习惯了直接调用 std::sort 或库函数，却往往忽略了底层的实现逻辑。然而，只有深入理解了从 O(N^2) 到 O(N log N) 的演进过程，掌握了递归与非递归的转换思想，才能在面对复杂场景时游刃有余。

本文将对计算机科学中经典的八大排序算法进行深度总结。不只是简单的代码罗列，更包含核心思想解析、边界条件处理、非递归优化方案以及性能对比。希望通过这篇文章，帮你彻底夯实算法基础。

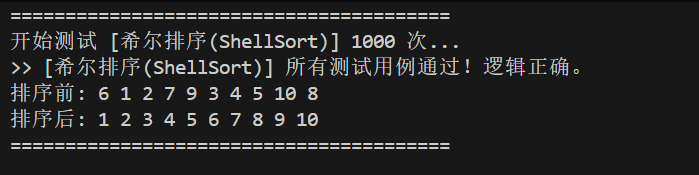
这里为了方便验证以下排序的结果，我写了一个验证函数，通过随机生成的数进行排序，然后再与库中的sort进行比较结果验证是否正确：

cpp 复制代码 
bool SortIsPass(function<void(vector<int>&)> sortFunc, string funcName)
{
    srand((unsigned int)time(NULL));
    const int N = 20;            // 数组大小
    const int TEST_COUNT = 1000; // 测试次数
    bool pass = true;

    cout << "========================================" << endl;
    cout << "开始测试 [" << funcName << "] " << TEST_COUNT << " 次..." << endl;

    for (int k = 0; k < TEST_COUNT; ++k)
    {
        std::vector<int> v(N);
        // 生成随机数
        for (int i = 0; i < N; ++i) v[i] = rand() % 100;
        
        // 备份一份给标准库排序用
        std::vector<int> v_copy = v;

        // 调用传入的排序算法
        sortFunc(v);

        // 调用标准库排序
        std::sort(v_copy.begin(), v_copy.end());

        // 对比结果
        if (v != v_copy) {
            cout << ">> [" << funcName << "] 测试失败！" << endl;
            cout << "原数据(已排序): "; PrintArray(v_copy);
            cout << "结果:       "; PrintArray(v);
            pass = false;
            break;
        }
    }

    if (pass) {
        cout << ">> [" << funcName << "] 所有测试用例通过！逻辑正确。" << endl;
        
        // 简单展示一次效果
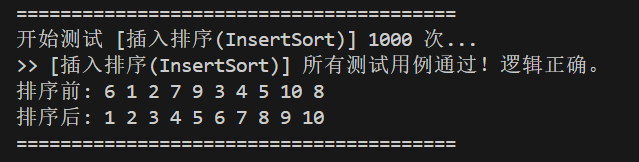
        vector<int> demo = { 6, 1, 2, 7, 9, 3, 4, 5, 10, 8 };
        cout << "排序前: "; PrintArray(demo);
        sortFunc(demo);
        cout << "排序后: "; PrintArray(demo);
    }
    cout << "========================================" << endl << endl;

    return pass;
}

1. 插入排序

1.1 直接插入排序

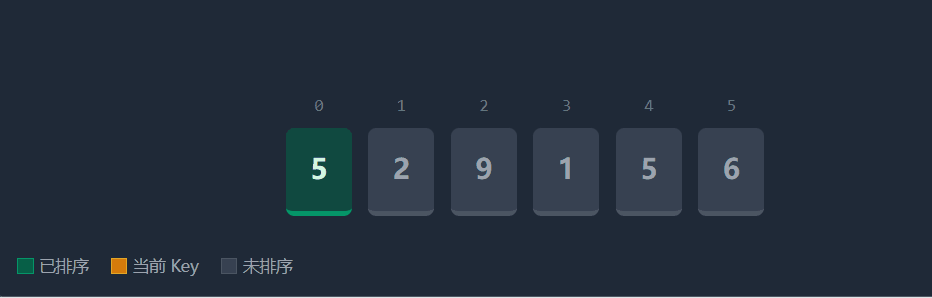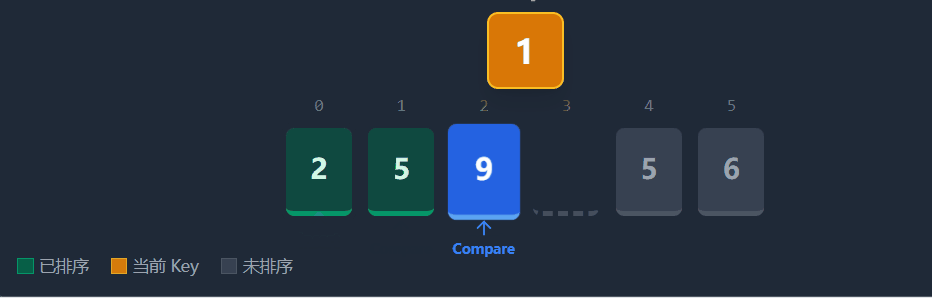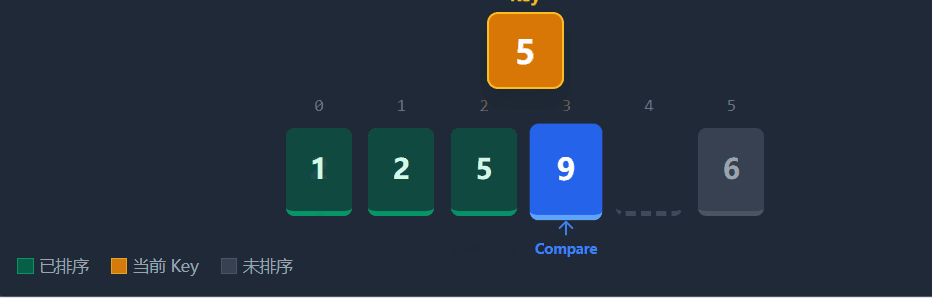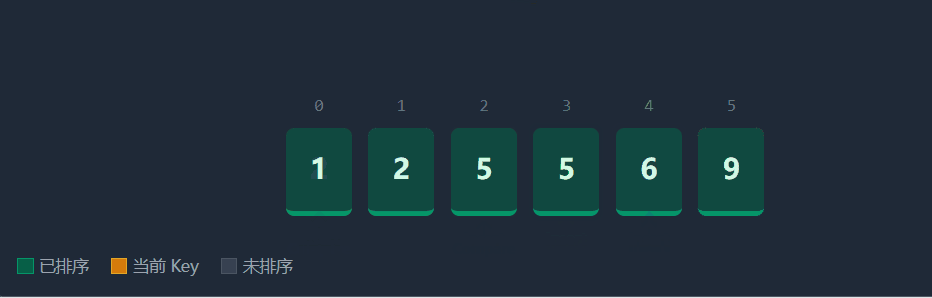
直接插入排序的思想是将待排序的数组分为已排序 和未排序 两部分。初始时，我们视下标 0 的元素为"已排序区间"。随后，我们从下标 1 开始，依次取出数据作为 key，将其与前面已排序的数据从后向前比较，插入到合适的位置。

具体流程（以升序为例）：在每一趟排序中，我们定义一个下标end（指向已排序区间的末尾）和key（待插入元素，即end + 1位置的值）。

1）比较key与nums[end]的大小。

2）如果key小于nums[end]，说明key应该排在nums[end]的前面，我们将nums[end]向后面移动一位（覆盖end + 1），并将end 向前移动一位（end--）。

3）重复步骤1-2，直到找到一个位置，使得nums[end]小于等于key，或者end以及减为-1（说明key比前面所有值都小）。

4）最后，将key放入end + 1的位置。

**时间复杂度：**O(N^2)

演示流程：

具体实现代码 ：

cpp 复制代码 
void InsertSort(vector<int>& nums)
{
    for (int i = 0; i < nums.size() - 1; i++)
    {
        int end = i;
        int key = nums[end + 1];
        while (end >= 0)
        {
            if (key < nums[end]){
                nums[end + 1] = nums[end];
                end--;
            }
            else{
                break;
            }
        }
        // 无论是 break 跳出，还是 end 减到 -1，key 都应该放在 end + 1
        nums[end + 1] = key;
    }
}

测试排序：

1.2 希尔排序

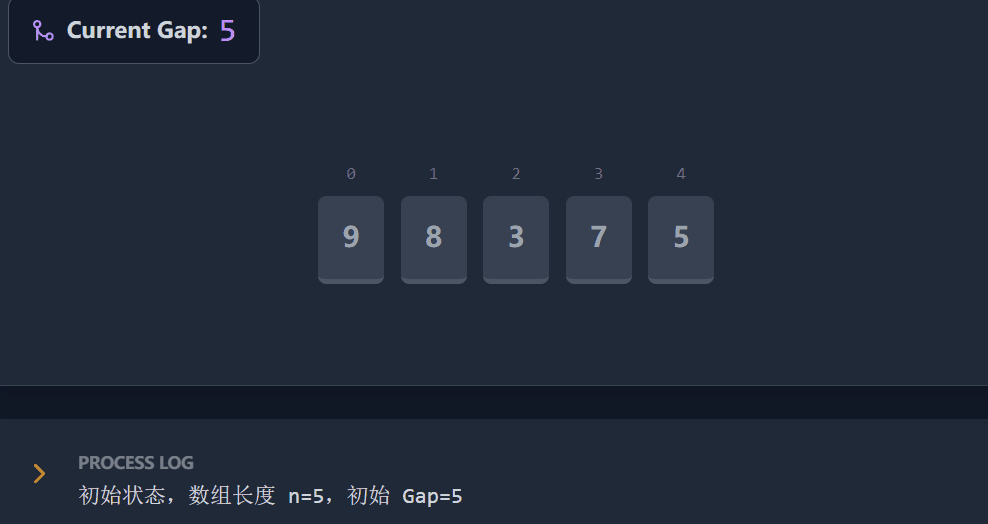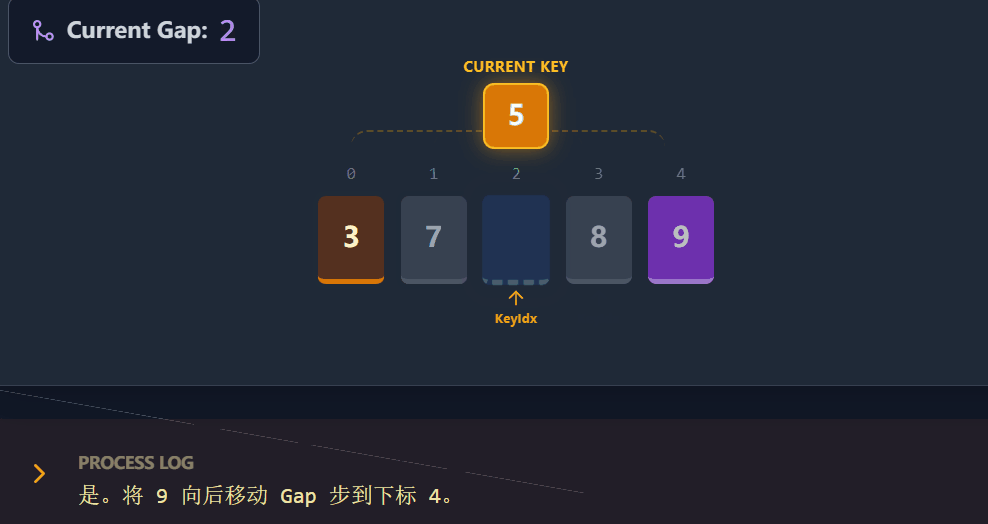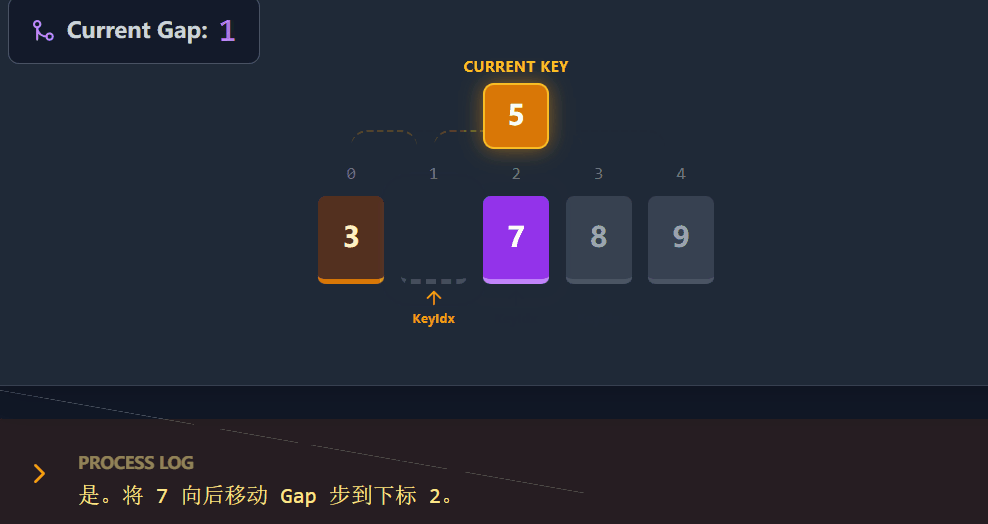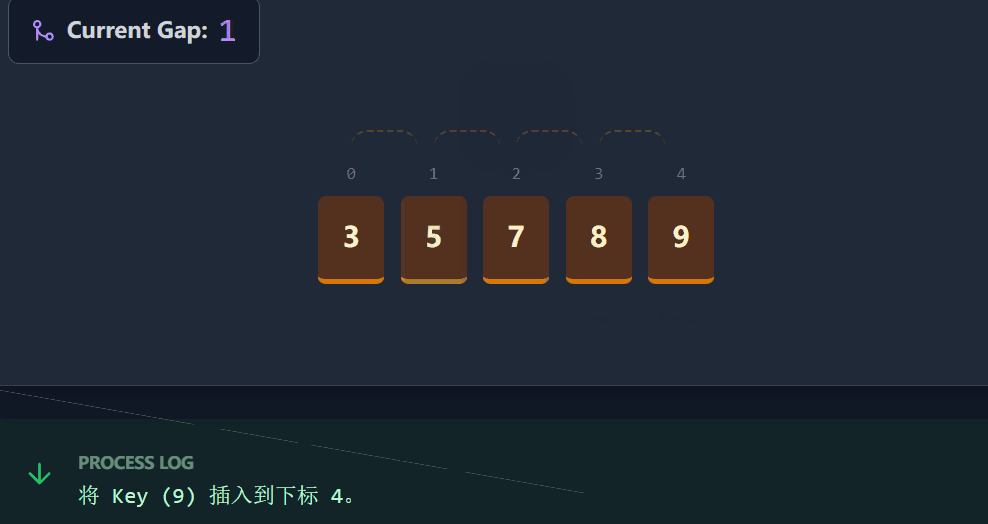
希尔排序是直接插入排序的改良版 （也称为缩小增量排序），直接插入排序在数据"几乎有序"时效率极高，但在数据乱序且最小元素在最后面时，需要移动大量元素。希尔排序旨在通过预排序的，让大的数快速跳到后面，小的数快速跳到前面，使数组接近有序，最后在进行一次直接插入排序。

具体流程（以升序为例）： 希尔排序本质上是分组插入排序 。我们将数组按间隔 gap 分成若干组，每组内部进行直接插入排序。 每一趟排序中，我们定义下标 end（指向当前组已排序部分的末尾），待插入元素 key 位于 end + gap。

  1. 比较key与nums[end]的大小。

  2. 如果key小于nums[end]，说明key应该排在nums[end]的前面（在当前分组内），我们将nums[end]向后面移动gap位（覆盖end + gap），并将end 向前移动gap位（end -= gap）。

  3. 重复步骤 1-2，直到找到一个位置，使得 nums[end] 小于等于 key，或者 end 越界（减为负数）。

  4. 最后，将key放入end + gap的位置。

**时间复杂度：**O(N^2)

演示流程：

代码演进过程：

阶段一：理解分组预排序 假设 gap = 3，我们相当于把数组分成了3组，分别对这3组进行插入排序。

cpp 复制代码 
void ShellSort_Part(vector<int>& arr) {
    int n = arr.size();
    int gap = 3; // 假设 gap 为 3

    // 第一层循环：依次处理每一组（共 gap 组）
    for (int j = 0; j < gap; j++) {
        // 第二层循环：对当前组进行插入排序
        // i 每次增加 gap，相当于跳着访问
        for (int i = j; i < n - gap; i += gap) {
            int end = i;
            int key = arr[end + gap];
            
            while (end >= 0) {
                if (key < arr[end]) {
                    arr[end + gap] = arr[end]; // 移动 gap 位
                    end -= gap;
                } else {
                    break;
                }
            }
            arr[end + gap] = key;
        }
    }
}

阶段二：优化代码逻辑（多组并排） 仔细观察可以发现，我们不需要用三层循环（一组一组排）。我们可以直接从 gap 位置开始遍历数组，交替 对各组进行排序。这不改变算法逻辑，但代码更简洁。 即：for (int i = 0; i < n - gap; i++)。

阶段三：动态调整 gap（最终完整版本） 预排序可以进行多次。gap 越大，数据跳跃越快；gap 越小，数据越接近有序。 通常策略是 gap = n，然后每次 gap = gap / 2（或者 gap = gap / 3 + 1），直到 gap = 1。当 gap = 1 时，就是标准的直接插入排序，此时数组已经非常有序，排序极快。

最终代码：

cpp 复制代码 
void ShellSort(vector<int>& arr) {
    int n = arr.size();
    int gap = n;

    // 1. gap > 1 时是预排序
    // 2. gap == 1 时是直接插入排序，排完即有序
    while (gap > 1) {
        gap /= 2; // 调整 gap，常见为 /2 或者 /3 + 1
        
        // 这一层循环实现了"多组并排"
        // i 从 0 开始，依次处理第 1 组、第 2 组... 的元素
        for (int i = 0; i < n - gap; i++) {
            int end = i;
            int key = arr[end + gap];

            while (end >= 0) {
                if (key < arr[end]) {
                    arr[end + gap] = arr[end];
                    end -= gap;
                } else {
                    break;
                }
            }
            arr[end + gap] = key;
        }
    }
}

测试排序：

2. 选择排序

2.1 选择排序--双向优化版

选择排序是一种简单直观的排序算法。这里我们介绍一种优化方案 ：每一次遍历不再只选一个数，而是同时选出最小值 和最大值，分别放置在序列的头部和尾部。这样可以将排序的迭代次数减少一半。

具体流程（以升序为例）：

  1. 定义 begin 和 end 分别指向待排序区间的头部和尾部。

  2. 遍历 [begin, end] 区间，找到最小值的下标 mini 和最大值的下标 maxi。

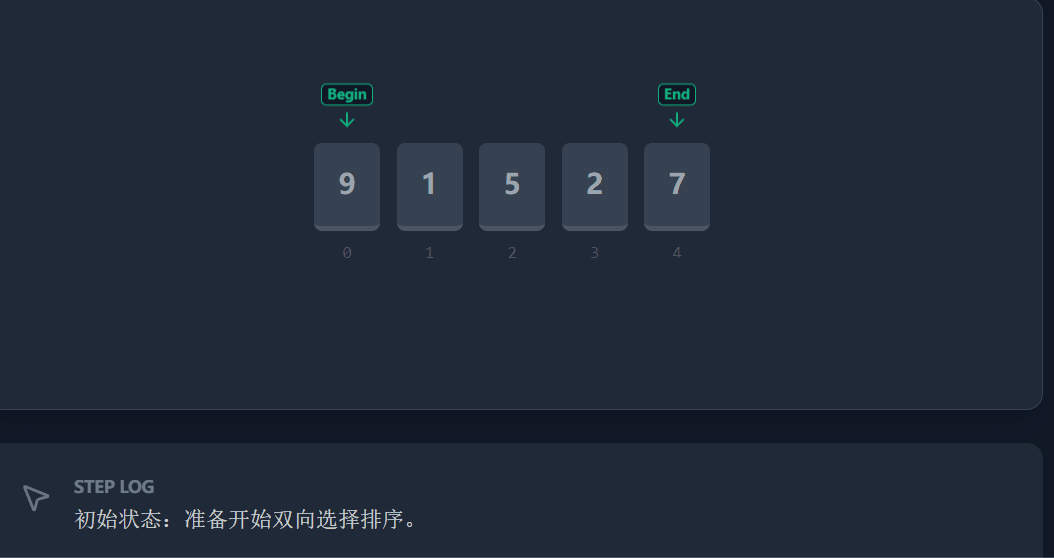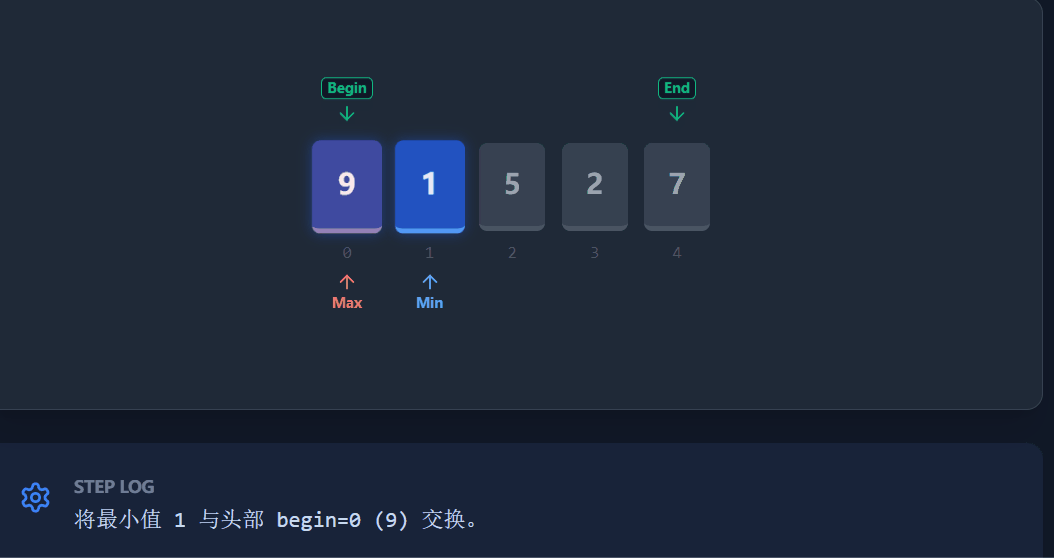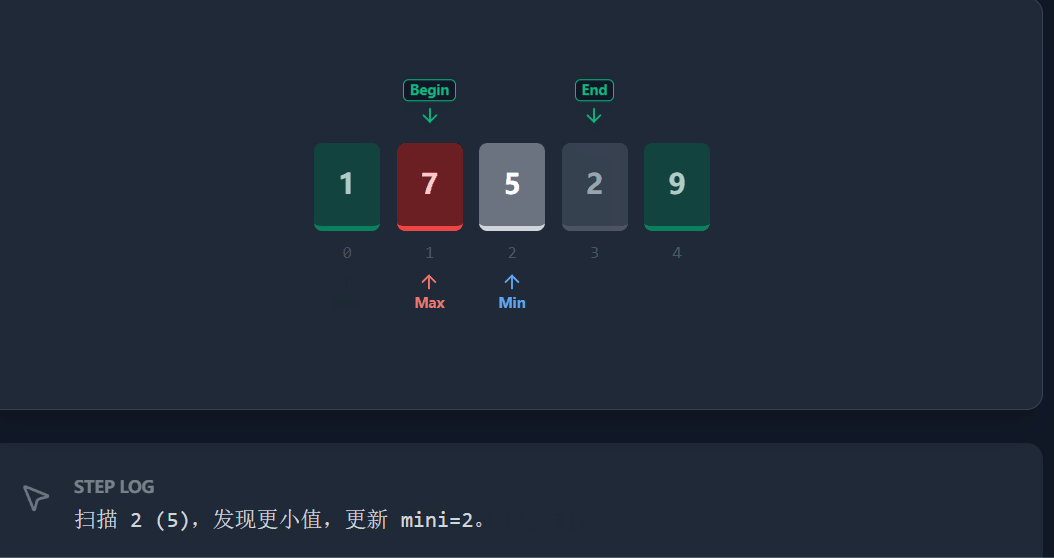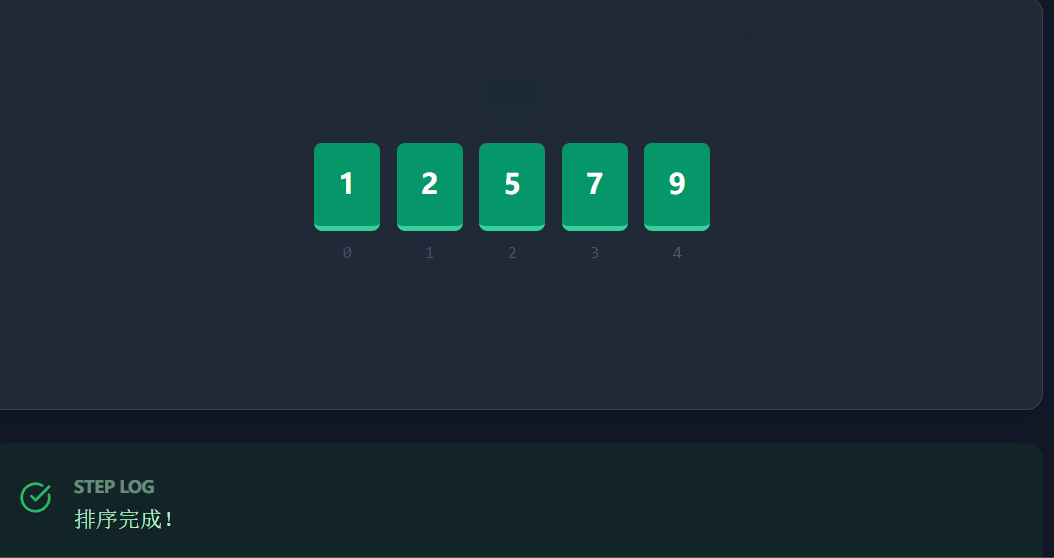
  3. 核心交换步骤：

    1）先将 mini 位置的数值与 begin 位置交换（把最小的放前面）。

    2）关键修正 ：如果此时 maxi 刚好在 begin 位置，说明刚才的交换把最大值移到了 mini 位置。我们需要更新 maxi = mini。

    3）最后将 maxi 位置的数值与 end 位置交换（把最大的放后面）。

  4. 执行 ++begin 和 --end，缩小待排序区间。

  5. 重复上述步骤，直到 begin >= end。

时间复杂度：O(N^2)

演示 流程：

具体代码：

cpp 复制代码 
void SelectSort(vector<int> &arr)
{
    int begin = 0, end = arr.size() - 1;
    while (begin < end)
    {
        int mini = begin, maxi = begin;
        for (int i = begin + 1; i <= end; i++)
        {
            if (arr[i] < arr[mini]){
                mini = i;
            }

            if (arr[maxi] < arr[i]){
                maxi = i;
            }
        }

        std::swap(arr[mini], arr[begin]);
        if (maxi == begin){
            maxi = mini;
        }
        std::swap(arr[maxi], arr[end]);

        ++begin;
        --end;
    }
}

测试排序：

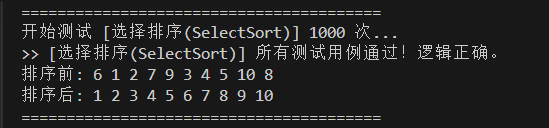
2.2 堆排序

堆排序是利用堆这种数据结构设计的一种排序算法。它通过将数组视为一颗完全二叉树，并利用堆顶是"最值"的性质，通过不断交换和调整完成排序。堆排序是一种原地排序，不需要额外空间。

关键点：

  • 升序排序 ：需要建立大顶堆。因为我们要每次取堆顶（最大值）放到数组最后。

  • 降序排序 ：需要建立小顶堆。

具体流程（以升序为例）：

1）建堆：我们需要将原数组调整为一个大顶堆。为了保证子数组也是堆，我们采用向下调整的方式。从最后一个非叶子节点开始，从后往前遍历到根节点（下标0）。

注意：最后一个非叶子节点的计算公式：(n - 1 - 1) / 2，其中n是数组长度。

2）排序：利用堆顶元素永远是当前堆中的最大值的性质：

  • 定义end指向数组的最后一个位置（n - 1）。

  • 将堆顶元素（arr[0]）与arr[end]交换。此时，最大值就被放到了末尾。

  • 交换后，堆的结构被破坏，需要对堆顶进行向下调整，恢复大顶堆的性质。注意此时调整的范围是0到end - 1（已排好的末尾元素不再参与）。

  • 执行end--，重复上述步骤，直到end<=0。

时间复杂度：O(NlogN)

演示流程：

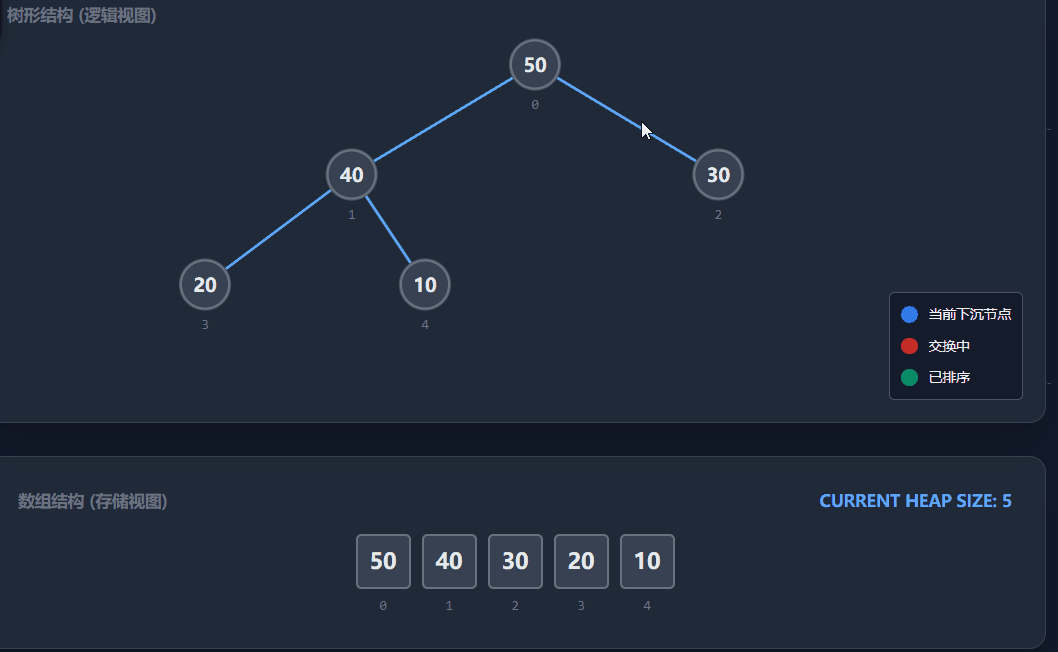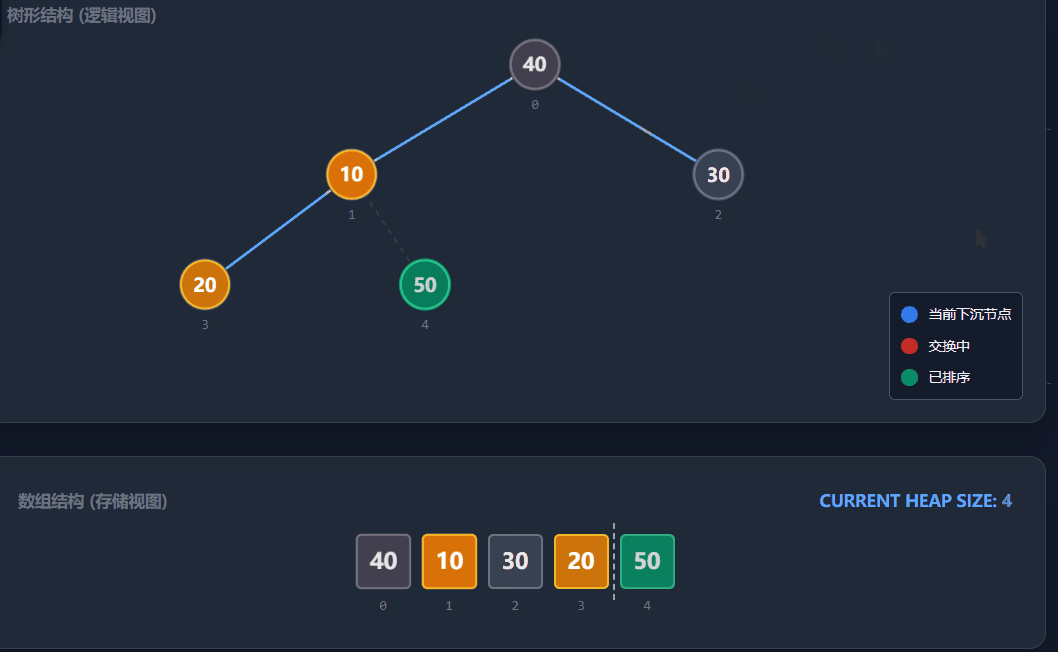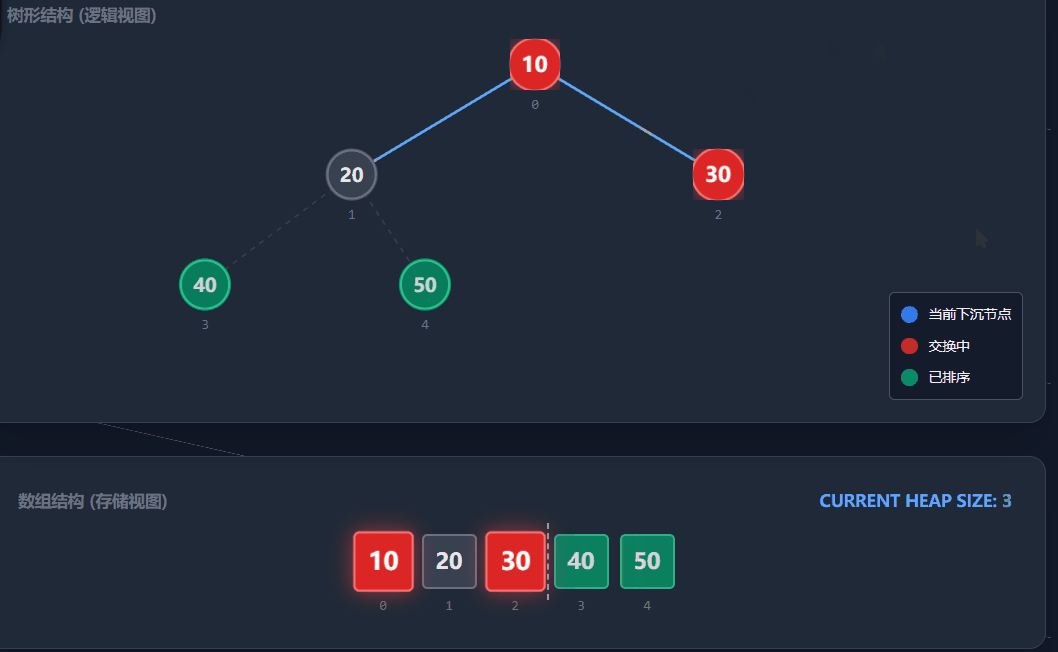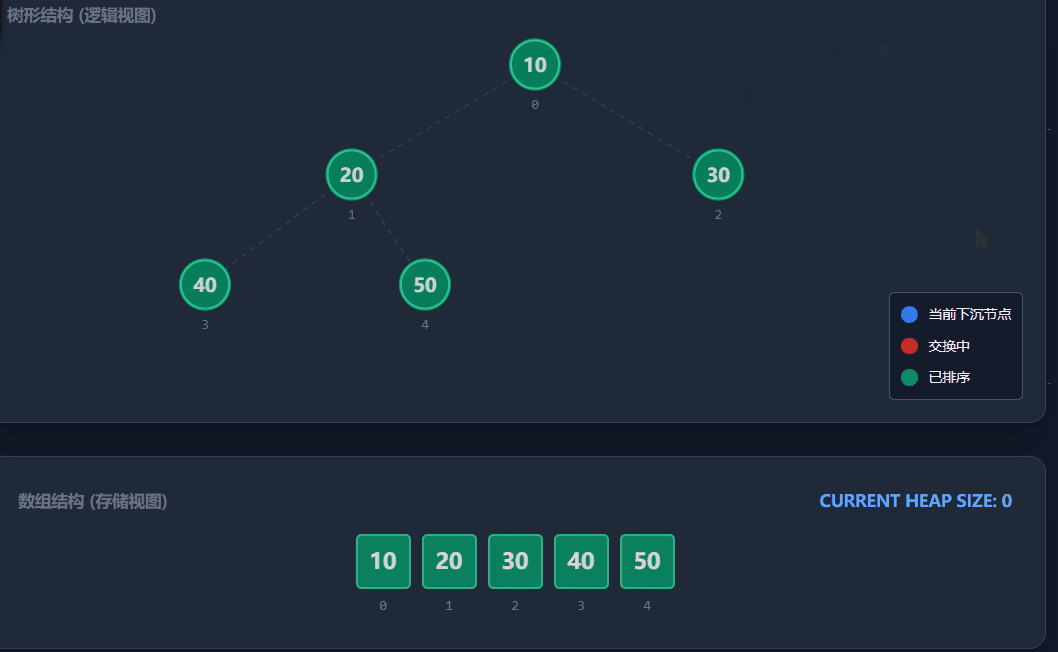
具体实现代码：

cpp 复制代码 
void AdjustDown(int parent, int n, vector<int>& arr)
{
	// 左孩子
	int child = parent * 2 + 1;
	while (child < n)
	{
		// 1. 选出左右孩子中较大的那个
        // child + 1 < n 保证右孩子存在
		if (child + 1 < n && arr[child + 1] > arr[child]) {
			child++;
		}

		if (arr[child] > arr[parent]) {
			std::swap(arr[child], arr[parent]);
			// 继续沿着路径向下调整
			parent = child;
			child = parent * 2 + 1;
		}
        // 如果父亲比孩子大，说明已经符合堆的性质，停止调整
		else
			break;
	}
}

void HeapSort(vector<int>& arr)
{
	int n = arr.size();
	// 1. 建堆
    // 从最后一个非叶子节点开始，依次向前调整
	for (int i = (n - 1 - 1) / 2; i >= 0; i--){
		AdjustDown(i, n, arr);
	}

    // 2. 排序
	int end = n - 1;
	while (end > 0)
	{
		// 将堆顶（最大值）交换到数组末尾
		std::swap(arr[0], arr[end]);
		// 对剩余的堆顶元素进行向下调整，恢复堆性质
        // 注意：此时传入的大小是 end，即排好的部分不再处理
		AjustDown(0, end, arr);
		end--;
	}
}

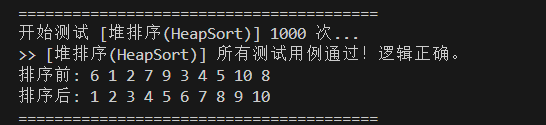
测试排序：

3. 交换排序

3.1 冒泡排序

冒泡排序的核心思想是通过相邻元素的两两比较和交换，像水底的气泡一样，将最大的元素"浮"到数组的顶端（末尾）。

具体流程（以升序为例）：

  1. 外层循环：控制排序的趟数。每一趟排序结束，都会有一个当前最大的数被移动到最终位置（即数组末尾）。

  2. 内层循环：进行两两比较。

    1）遍历区间 [1, n - j)。

    2）比较相邻元素：如果前一个元素 arr[i-1] 大于后一个元素 arr[i]，则交换它们。

    3）随着 j 的增加，尾部有序区越来越长，因此内层循环需要比较的元素越来越少（n - j）。

  3. 进阶优化：

    1）定义一个标志位 flag。

    2）如果在某一趟遍历中没有发生任何交换，说明数组已经有序，无需进行后续的排序，直接跳出循环。

具体代码：

cpp 复制代码 
void bubbleSort(vector<int> &arr)
{
    int n = arr.size();

    // j 表示已经排好序的元素个数（从后往前）
    // 同时也代表当前是第几趟排序
    for (int j = 0; j < n - 1; j++)
    {
        // 标志位：本趟是否发生交换
        bool flag = false;
        // 每一趟将最大的元素"冒泡"到 n-1-j 的位置
        for (int i = 1; i < n - j; i++)
        {
            if (arr[i - 1] > arr[i])
            {
                std::swap(arr[i - 1], arr[i]);
                flag = true;
            }
        }
        // 如果标志位没有被修改，说明此时数据是有序的
        if(!flag){
            break;
        }
    }
}

测试排序：

3.2 快速排序 - Hoare 版本

快速排序是目前应用最广泛的排序算法之一（如 C++ STL 的 std::sort 在某些阶段就使用了快排）。 它的核心思想是分治法：

  1. 选基准：任选一个元素作为基准（Key）。

  2. 划分（Partition）：将小于 Key 的元素放到左边，大于等于 Key 的元素放到右边。此时，Key 就处于了最终有序数组的正确位置。

  3. 递归：将 Key 左边和右边的子区间视作新的数组，重复上述过程，直到区间长度为 0 或 1，此时数组整体有序。

具体流程（Hoare 版本）： 每一趟排序的目的是确定 Key 的最终位置

1）初始化：

  • 选取最左边的元素作为 key，记录其下标 keyi = left。

  • 定义双指针 L (left) 和 R (right)，分别指向区间的头和尾

2）探测与交换：

  • R 先走 ：从右向左找比 key 小的数，找到后停下。

  • L 后走 ：从左向右找比 key 大的数，找到后停下。

  • 交换 arr[L] 和 arr[R]，将小的扔到左边，大的扔到右边。

3）放置基准值：

  • 当 L 和 R 相遇时，循环结束。

  • 关键步骤 ：交换 arr[keyi] 和 arr[L]（相遇点）。此时 key 归位。

4）递归：

  • 以 keyi 为界，递归处理左右子区间 [begin, keyi - 1] 和 [keyi + 1, end]。

3.2.1核心难点：为什么必须让 Right (右指针) 先走？

这是为了保证相遇位置的值一定要小于等于 Key。如果相遇位置的值比 Key 大，交换后 Key 就会跑到右半区（大数区），破坏排序逻辑。 我们看相遇时的三种情况（假设 Key 在最左边）：

  1. R 停住，L 撞上 R ： R 既然停住了，说明 R 指向的值一定小于 Key。L 撞上 R，相遇点也是这个小值。交换后 Key 遇到小值，逻辑正确。

  2. L 停住，R 撞上 L ： 这种情况是不存在的，因为 R 先走。R 只会找小的，如果没找到会一直走到 L 的位置。 注：如果是上一轮交换后 L 停在了一个小值上，R 走过来之前 L 不会动。R 跨过大值继续找小值，或者 R 直接撞上上一轮的 L（此时 L 是交换后的小值），或者 R 走到 Keyi。 更准确的说法是：R 动的时候 L 是不动的。R 既然能走到 L 所在的位置，说明 R 一路上都没找到比 Key 小的，直到撞上了 L。而 L 所在的位置（如果是刚发生过交换）一定是小于 Key 的。

  3. R 一直走到 keyi： 说明右边所有数都比 Key 大，直接自己和自己交换，逻辑也正确。

结论：R 先走，保证了相遇点的数据必然是 <= Key 的。

具体实现代码：

cpp 复制代码 
void qSort(vector<int>& arr, int begin, int end) {
    // 递归结束条件
    if (begin >= end) {
        return;
    }

    int left = begin;
    int right = end;
    int keyi = left; // 选取最左边为 key

    while (left < right) {
        // 1. 右边先走，找小
        // 注意：要加上 left < right 防止越界，且是 >= 才能略过相等的值
        while (left < right && arr[right] >= arr[keyi]) {
            right--;
        }

        // 2. 左边再走，找大
        while (left < right && arr[left] <= arr[keyi]) {
            left++;
        }

        // 3. 交换左右值
        std::swap(arr[left], arr[right]);
    }

    // 4. 相遇后，交换 key 与相遇点
    std::swap(arr[keyi], arr[left]);
    keyi = left; // 更新 keyi 到正确的位置

    // 5. 递归处理左右区间
    qSort(arr, begin, keyi - 1);
    qSort(arr, keyi + 1, end);
}
3.2.2优化方案

优化 1：三数取中法

当数组已经有序（如 1, 2, 3, 4, 5）时，如果每次取最左边做 Key，快排会退化为单支树，时间复杂度由 O(N log N) 变为 O(N^2)。

解决： 取 left、right、mid 三个位置的值，选择中间那个值作为 Key，并交换到 left 位置，这样可以避免最坏情况。

cpp 复制代码 
// 三数取中
int GetMid(vector<int>& a, int left, int right)
{
    int mid = left + (right - left) / 2;
    if (a[left] < a[mid])
    {
        // left < mid < right
        if (a[mid] < a[right])
            return mid;
        //  right < left < mid
        else if (a[left] > a[right])
            return left;
        // left < right < mid
        else
            return right;
    }
    // left > mid
    else
    {
        if (a[mid] > a[right])
            return mid;
        else if (a[right] < a[left])
            return right;
        else
            return left;
    }
}

// 在 qSort 开头调用：
// int midi = GetMid(arr, begin, end);
// std::swap(arr[begin], arr[midi]); // 把中间值换到最左边，后续逻辑不变

优化2：小区间插入排序 快排递归就像一棵二叉树，最后几层的递归调用次数占据了总调用次数的 90% 以上，但处理的数据量却很小。 解决： 当区间数据量较少（例如 count < 10）时，不再递归，直接使用插入排序。插入排序在处理小规模、接近有序的数据时效率极高。

cpp 复制代码 
void qSort(vector<int>& arr, int begin, int end) {
    if (begin >= end) return;

    // 优化：小区间直接使用插入排序
    if (end - begin + 1 < 10) {
        // InsertSort(arr, begin, end); 
        return;
    }

    // ... 剩下的快排逻辑 ...
}

测试排序：

3.3 非递归快排

递归实现的本质是利用系统栈来保存每一层调用的栈帧。非递归快排的核心思想就是手动利用 std::stack 数据结构来模拟这个递归过程。

具体流程：

  1. 将整个数组的区间 [0, n-1] 压入栈中。

  2. 当栈不为空时，弹出栈顶的区间 [begin, end]。

  3. 对该区间进行一次划分排序（此处使用的双指针法，使用Hoare大佬的也可以），得到基准值下标 keyi。

  4. 判断 keyi 的左右子区间是否有效，若有效则将子区间 [begin, keyi-1] 和 [keyi+1, end] 压入栈中，等待后续处理。

具体代码：

cpp 复制代码 
int PartSort(vector<int>& arr, int left, int right) {
    int keyi = left;
    int prev = left, cur = left + 1;
    while (cur <= right) {
        if (arr[cur] < arr[keyi] && ++prev != cur)
            std::swap(arr[prev], arr[cur]);
        cur++;
    }
    std::swap(arr[prev], arr[keyi]);
    return prev; // 返回基准值的最终位置
}

// 非递归主函数
void QuickSortNonR(vector<int>& arr) {
    if (arr.empty()) return;

    stack<pair<int, int>> st;
    // 1. 初始区间入栈
    st.push({0, arr.size() - 1});

    while (!st.empty()) {
        // 2. 取出栈顶区间
        pair<int, int> range = st.top();
        st.pop();
        
        int begin = range.first;
        int end = range.second;

        // 3. 调用划分逻辑获得 keyi
        int keyi = PartSort(arr, begin, end);

        // 4. 将有效的左右子区间入栈
        if (keyi + 1 < end) {
            st.push({keyi + 1, end});
        }
        if (begin < keyi - 1) {
            st.push({begin, keyi - 1});
        }
    }
}

测试排序：

4. 归并排序

4.1 递归版 - 归并排序

归并排序是建立在分治法基础上的经典排序算法。 它的核心思想非常直观：

  1. 分：将数组一分为二，一直分到无法再分为止（即区间只剩一个元素，此时默认有序）。

  2. 治：将两个有序的子区间"归并"成一个更大的有序区间。 通过不断地递归和归并，最终让整个数组变得有序

具体流程（以升序为例）：

  1. 分解区间 ： 计算中间下标 mid = (begin + end) / 2，将当前区间划分为 [begin, mid] 和 [mid + 1, end]。

  2. 递归调用 ： 对左右两个子区间分别调用归并排序。这是一个后序遍历的过程，意味着我们深入到最底层（单个元素）后，才开始向上层层返回并合并。

  3. 合并有序区间（核心） ： 当左右子区间递归返回时，它们已经是两个有序序列了。我们需要借助一个临时数组 tmp：

    • 比较两个子区间的队头元素，将较小的那个放入 tmp 数组。

    • 移动被选中元素的指针，继续比较。

    • 如果某个区间遍历完了，将另一个区间剩余的元素直接拷贝到 tmp 后面。

    • 最后，将 tmp 中排好序的数据拷贝回原数组，完成这一趟归并。

时间复杂度： O(N log N) 空间复杂度： O(N)

具体代码：

cpp 复制代码 
// 归并排序的子函数
void _MergeSort(vector<int>& arr, vector<int>& tmp, int begin, int end) {
    // 递归结束条件：区间只有一个元素或不存在
    if (begin >= end) {
        return;
    }

    // 1. 分解：计算中间位置
    int mid = begin + (end - begin) / 2;

    // 2. 递归：分别对左右区间进行排序
    // [begin, mid] 和 [mid+1, end]
    _MergeSort(arr, tmp, begin, mid);
    _MergeSort(arr, tmp, mid + 1, end);

    // 3. 归并：将两个有序区间合并
    int begin1 = begin, end1 = mid;
    int begin2 = mid + 1, end2 = end;
    
    // tmp 数组的存放下标
    int index = begin;

    // 比较两个区间，选小的放入 tmp
    while (begin1 <= end1 && begin2 <= end2) {
        if (arr[begin1] < arr[begin2]) {
            tmp[index++] = arr[begin1++];
        } else {
            tmp[index++] = arr[begin2++];
        }
    }

    // 处理剩余元素（两个 while 只会执行其中一个）
    while (begin1 <= end1) {
        tmp[index++] = arr[begin1++];
    }
    while (begin2 <= end2) {
        tmp[index++] = arr[begin2++];
    }

    // 4. 拷贝：将排好序的 tmp 数据拷回原数组 arr
    for (int i = begin; i <= end; i++) {
        arr[i] = tmp[i];
    }
}

// 归并排序主函数
void MergeSort(vector<int>& arr) {
    int n = arr.size();
    // 预先开辟空间，避免递归中频繁申请
    vector<int> tmp(n);
    _MergeSort(arr, tmp, 0, n - 1);
}

测试排序：

4.2 非递归版 - 归并排序

归并排序的非递归版是直接通过循环来模拟递归中"归"的过程。我们跳过递归分解的步骤，直接视作数组中的元素已经是通过 gap=1 分组的有序序列，然后不断扩大 gap 进行合并。

具体流程：

  1. 定义步长 gap：控制每次合并的子区间长度，初始化为 1。

  2. 循环归并：

    • 每轮归并，将数组分为若干组，每组包含两个子区间：[begin1, end1] 和 [begin2, end2]。

    • 计算下标：

      • begin1 = i

      • end1 = i + gap - 1

      • begin2 = i + gap

      • end2 = i + 2 * gap - 1

    • 边界修正（核心难点） ： 由于数组长度 n 不一定能被 2 * gap 整除，计算出的下标极易越界，需要分类处理：

      1. 没有第二组区间 (begin2 >= n)：第一组区间已经是之前的排序结果，无需合并，直接跳过。

      2. 第一组区间都不完整 (end1 >= n)：同上，不需要合并。

      3. 第二组区间只有部分 (end2 >= n)：此时需要合并，但需修正 end2 = n - 1。

  3. 拷贝数据 ：将 tmp 中归并好的数据拷贝回原数组。

    • 注意：建议归并完一组就拷贝一组（部分拷贝），这样处理边界问题最简单，避免全量拷贝导致的尾部数据覆盖错误。

    • 举个例子：假设数组 arr = [10, 9, 7]，n = 3。 此时 gap = 1。初始化 tmp = [0, 0, 0] (vector 默认初始化为0)。tmp应该是[10，9，0]，此时再将tmp拷贝回去会将arr污染，这是错误的。

  4. 迭代 ：gap *= 2，直到 gap >= n，排序完成。

具体代码：

cpp 复制代码 
void MergeSortNonR(vector<int>& arr) {
    int n = arr.size();
    vector<int> tmp(n);
    // 控制每个归并区间的元素个数
    int gap = 1;

    while (gap < n) {
        // 每次分组划分两段区间，两两区间进行归并
        // i为第一段区间的开始
        for (int i = 0; i < n; i += gap * 2) {
            int begin1 = i, end1 = begin1 + gap - 1;
            int begin2 = end1 + 1, end2 = begin2 + gap - 1;
            int start = begin1;

            // 只有第一段区间有数据时不需要归并 
            if (end1 >= n || begin2 >= n) {
                break;
            }

            // 第二段区间有元素但是个数小于gap个时需要继续归并
            if (end2 >= n) {
                end2 = n - 1;
            }

            while (begin1 <= end1 && begin2 <= end2) {
                if (arr[begin1] < arr[begin2]) {
                    tmp[start++] = arr[begin1++];
                }
                else {
                    tmp[start++] = arr[begin2++];
                }
            }

            // 继续合并剩下的元素
            while (begin1 <= end1) {
                tmp[start++] = arr[begin1++];
            }

            while (begin2 <= end2) {
                tmp[start++] = arr[begin2++];
            }

            for (int j = 0; j < n; j++) {
            arr[j] = tmp[j];
            }
        }

        gap *= 2;
    }
}

测试排序：

5. 非交换排序

5.1 计数排序

计数排序是一种非比较排序算法。不同于快排或归并通过比较数据大小来排序，计数排序的核心思想是"空间换时间"。

它利用数组下标的自然有序性，统计每个数字出现的次数，然后再把这些数字"铺"回原数组。对于范围比较集中的整数排序，它的速度极快，甚至超过 O(N log N) 的算法。

具体流程（以升序为例）：

  1. 确定范围 ： 遍历数组，找到最大值 maxNum 和最小值 minNum，计算出数据的范围 range = maxNum - minNum + 1。

  2. 统计计数（相对映射） ： 开辟一个大小为 range 的计数数组 count。 为了处理负数和节省空间，我们采用相对映射 ：数值 val 对应的下标是 val - minNum。遍历原数组，将每个数据出现的次数记录在 count 数组中。

  3. 回填排序 ： 遍历 count 数组。如果 count[i] 不为 0，说明原数组中有 count[i] 个大小为 i + minNum 的数据。我们将这些数据依次覆盖回原数组，完成排序。

时间复杂度： O(N + range) 空间复杂度： O(range)

局限性： 只适用于整数，且当数据范围（range）远大于数据个数（N）时，效率会很低且浪费空间。

具体代码：

cpp 复制代码 
void CountSort(vector<int>& arr) {
    // 1. 判空，防止 arr[0] 越界
    if (arr.empty()) return;

    int n = arr.size();
    int minNum = arr[0];
    int maxNum = arr[0];

    // 2. 找出最大值和最小值
    for (int i = 1; i < n; i++) {
        if (arr[i] < minNum) {
            minNum = arr[i];
        }
        if (arr[i] > maxNum) {
            maxNum = arr[i];
        }
    }

    // 3. 开辟计数数组
    int range = maxNum - minNum + 1;
    vector<int> count(range, 0);

    // 4. 统计次数（相对映射）
    for (int e : arr) {
        count[e - minNum]++;
    }

    // 5. 排序回写
    int index = 0;
    for (int i = 0; i < range; i++) {
        // count[i] 表示数值 (i + minNum) 出现的次数
        while (count[i] > 0) {
            arr[index++] = i + minNum;
            count[i]--;
        }
    }
}

6. 总结

经过对以上八种排序算法的学习，我们可以将它们根据时间复杂度 、空间复杂度 以及稳定性进行横向对比。

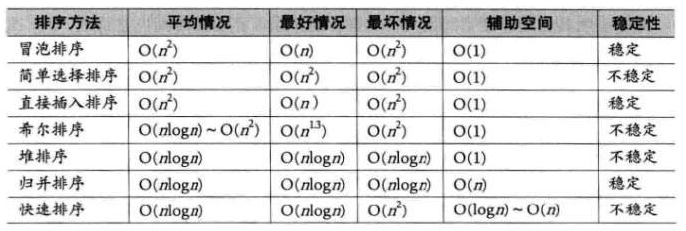
  1. 关于稳定性：

    • 稳定的排序：冒泡、插入、归并、计数。

      特点：通过相邻交换或额外空间辅助，保证了相等元素的相对顺序不被打乱。

    • 不稳定的排序：选择、希尔、堆排、快排。

      原因 ：它们都存在"跳跃式"交换（如快排的 swap、希尔的 gap、堆顶与堆尾交换），很容易打乱相等元素的顺序。

  2. 关于时间复杂度：

    • 第一梯队（慢） ：冒泡、插入、选择。适合数据量极小（如 N < 100）的情况。其中直接插入排序在数据接近有序时表现最好。

    • 第二梯队（快）：快排、归并、堆排、希尔。适合大数据量。

    • 快速排序 ：综合性能最强，是目前基于比较的排序中应用最广的（C++ STL sort 的主力）。

    • 归并排序：效率非常稳定，且是稳定的排序，但缺点是需要 O(N) 的额外空间。

    • 堆排序：空间效率高 O(1)，且最坏情况也能保证 O(N log N)，但不适合数据量太小（建堆有消耗）且缓存命中率不如快排。

  3. 特殊选手：

    计数排序 ：突破了比较排序的下限 0(N log N)，达到了线性时间。但局限性很大，只适用于整数 且范围集中的场景。

相关推荐
REDcker3 小时前
C++ 崩溃堆栈捕获库详解
linux·开发语言·c++·tcp/ip·架构·崩溃·堆栈
WW_千谷山4_sch3 小时前
洛谷P8653:[模板] [蓝桥杯 2017 国 C] 分考场（染色最小色数）
c++·算法·蓝桥杯·深度优先
兵哥工控3 小时前
MFC高精度方波发生器实现
c++·mfc
汉克老师3 小时前
GESP2025年12月认证C++五级真题与解析（判断题1-10）
c++·链表·贪心算法·排序·gesp5级·gesp五级
hk11244 小时前
【NLP/PatternRec】2026年度语义鸿沟分析与模糊模式识别基准索引 (Benchmark Index)
算法·自然语言处理·数据集·知识图谱·模式识别
hetao17338374 小时前
2025-12-31~2026-1-2 hetao1733837 的刷题笔记
c++·笔记·算法
争不过朝夕，又念着往昔4 小时前
C++AI
开发语言·c++·人工智能
敲上瘾4 小时前
C++11线程库指南：线程、锁、原子操作与并发编程实战
开发语言·c++·多线程
yyy(十一月限定版)4 小时前
算法——差分
算法
热门推荐
01GitHub 镜像站点02jdk21下载、安装（Windows、Linux、macOS）03Linux下V2Ray安装配置指南04手把手教你通过Gemini3 pro 学生认证，白用一年，手慢无！052025 最新教程：注册并切换到美区 Apple ID06安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）07Claude Code Skills 实用使用手册08UV安装并设置国内源09KGG转MP3工具|非KGM文件|解密音频10【踩坑笔记】50系显卡适配的 PyTorch 安装