目录
[类型 1:ABA 型(首尾相同)](#类型 1:ABA 型(首尾相同))
[类型 2:ABC 型(三色全不同)](#类型 2:ABC 型(三色全不同))
前言:
这是力扣的一个题目,很经典!就是找不到规律和找到规律,写代码完全不是一个级别!希望这篇可以给大家参考,我刚开始做的时候也想找规律,但是没找到,没有理解到意思!
题目:
你有一个 n x 3 的网格图 grid ,你需要用 红,黄,绿 三种颜色之一给每一个格子上色,且确保相邻格子颜色不同(也就是有相同水平边或者垂直边的格子颜色不同)。
给你网格图的行数 n 。
请你返回给 grid 涂色的方案数。由于答案可能会非常大,请你返回答案对 10^9 + 7 取余的结果。
示例 1:
- 输入:n = 1
- 输出:12
解释:总共有 12 种可行的方法:
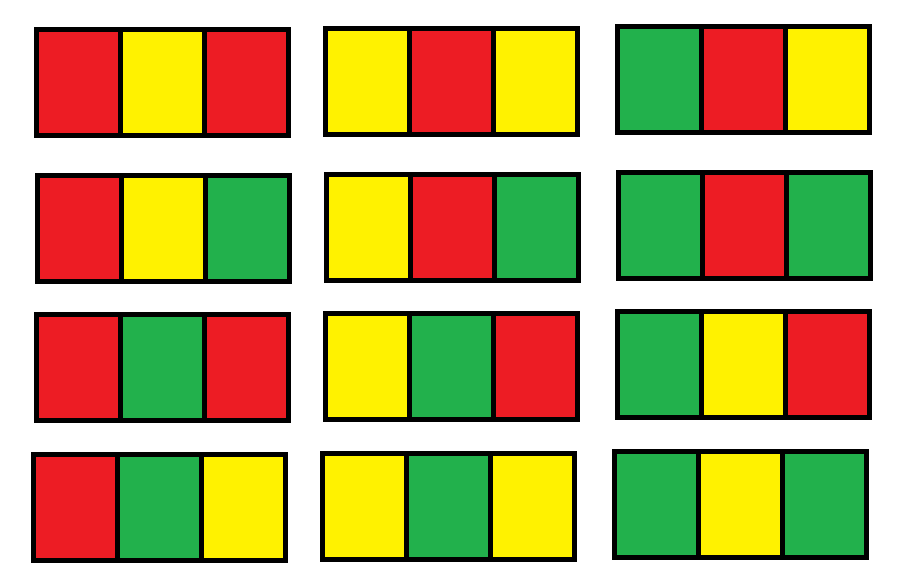
示例 2:
- 输入:n = 2
- 输出:54
示例 3:
- 输入:n = 3
- 输出:246
示例 4:
- 输入:n = 7
- 输出:106494
示例 5:
- 输入:n = 5000
- 输出:30228214
提示:
- n == grid.length
- grid[i].length == 3
- 1 <= n <= 5000
题目分析:
第一个代码,先考虑暴力搜索,枚举每个格子涂哪种颜色。
第二个代码,可以找到规律:
这个涂色问题的答案满足一个递推公式:
f(n) = 5 × f(n-1) - 2 × f(n-2)
其中:
f(1) = 12f(2) = 54f(3) = 5×54 - 2×12 = 270 - 24 = 246f(4) = 5×246 - 2×54 = 1122- ......
为了能让这个公式从 n=2 开始算,我们人为定义 一个 f(0) = 3(它没有实际意义,只是为了公式成立)。
验证一下:
f(2) = 5×f(1) - 2×f(0) = 5×12 - 2×3 = 60 - 6 = 54✅
代码一:
javaclass Solution { private static final int MOD = 1_000_000_007; // 全局 memo,记忆化的内容可以在不同测试数据间共享 private static Map<Integer, Integer> memo = new HashMap<>(); public int numOfWays(int n) { return dfs(n, 0, 0, 0); } // (i, j):当前位置 // preRow:上一行(i+1 行)的颜色 // curRow:当前这一行已填入的颜色 private int dfs(int i, int j, int preRow, int curRow) { if (i == 0) { // 所有格子都已涂色 return 1; // 找到一个合法方案 } if (j == 3) { // i 行已涂色 // 开始对 i-1 行涂色,curRow 变成 preRow return dfs(i - 1, 0, curRow, 0); } // 参数压缩到一个 int 中 int key = (i << 14) | (j << 12) | (preRow << 6) | curRow; if (memo.containsKey(key)) { // 之前计算过 return memo.get(key); } int res = 0; for (int color = 0; color < 3; color++) { // 枚举 (i, j) 的颜色 color if (preRow > 0 && color == (preRow >> (j * 2) & 3) || // 不能和下面相邻格子 (i+1, j) 颜色相同 j > 0 && color == (curRow >> ((j - 1) * 2) & 3)) { // 不能和左侧相邻格子 (i, j-1) 颜色相同 continue; } res = (res + dfs(i, j + 1, preRow, curRow | (color << (j * 2)))) % MOD; } memo.put(key, res); // 记忆化 return res; } }
代码二:
javapublic int numOfWays(int n) { final int MOD = 1_000_000_007; // 大数取模,防止溢出 int[] f = new int[n + 1]; f[0] = 3; // 虚拟值,让公式成立 f[1] = 12; // n=1 的真实答案 for (int i = 2; i <= n; i++) { // 用 long 防止中间计算溢出 f[i] = (int) ((f[i - 1] * 5L - f[i - 2] * 2L) % MOD); } // 因为减法可能导致负数,加 MOD 再取模确保结果 ≥0 return (f[n] + MOD) % MOD; }
代码一分析:
代码一采用DFS+记忆化的方法,从下往上逐格涂色:
-
状态表示:
-
(i, j)表示当前正在涂第 i 行第 j 列 -
preRow表示下一行(i+1行)的颜色状态(用6位二进制表示) -
curRow表示当前行已涂色的状态
-
-
状态转移:
-
每个格子尝试三种颜色
-
需要检查:不能与下方格子颜色相同,不能与左侧格子颜色相同
-
使用位运算高效地存储和检查颜色状态
-
-
记忆化优化:
-
将(i, j, preRow, curRow)压缩为一个整数作为key
-
避免重复计算相同状态
-
代码二分析(公式推导):
关键观察:每行只有两种模式
由于每行只有 3 个格子,且左右不能同色,我们可以枚举所有合法的单行涂色方式。
用三种颜色 A、B、C 表示,合法的行模式只有两类:
类型 1:ABA 型(首尾相同)
例如:红-黄-红、蓝-红-蓝
→ 满足:color[0] == color[2] != color[1]
类型 2:ABC 型(三色全不同)
例如:红-黄-蓝、蓝-绿-红
→ 满足:color[0] != color[1] != color[2] 且 color[0] != color[2]
💡 总共合法单行方案数:
- ABA 型:3 × 2 = 6 种(选首尾颜色 3 种,中间不同 2 种)
- ABC 型:3 × 2 × 1 = 6 种
- 共 12 种 → 所以
f(1) = 12
动态规划状态设计
设:
a[i]= 第i行是 ABA 型 的方案总数b[i]= 第i行是 ABC 型 的方案总数
则总方案数:f[i] = a[i] + b[i]
推导转移关系(关键!)
考虑第 i-1 行和第 i 行的颜色不能上下相同:
| 上一行类型 | 下一行可接的 ABA 数量 | 下一行可接的 ABC 数量 |
|---|---|---|
| ABA | 3 | 2 |
| ABC | 2 | 2 |
这个可以通过枚举验证(略,但标准结论如此)
于是得到递推式:
a[i] = 3 * a[i-1] + 2 * b[i-1] b[i] = 2 * a[i-1] + 2 * b[i-1]
所以总方案数:
f[i] = a[i] + b[i] = (3a + 2b) + (2a + 2b) = 5a + 4b
但我们希望只用 f[i] 表示。注意到:
f[i-1] = a[i-1] + b[i-1]f[i-2] = a[i-2] + b[i-2]
通过代数消元(或矩阵快速幂特征方程),可以推出一个二阶线性递推式:
f[i] = 5 * f[i-1] - 2 * f[i-2]
结语:
网格涂色问题展示了两种不同的解题思路:
-
通用方法(记忆化搜索):适合大多数约束满足问题,通过状态压缩和记忆化优化,可以处理中等规模的问题。
-
特殊方法(数学推导):通过发现问题的内在规律,得到简洁的递推公式,适用于大规模输入。
对于本题,由于n最大可达5000,数学递推方法明显更优。这也提醒我们,在解决算法问题时,不仅要掌握通用的解题技巧,也要注意观察问题特点,寻找更高效的专用解法。
推荐使用代码二的递推方法,它不仅效率高,而且代码简洁,是解决此类问题的优选方案。
希望这对大家有所帮助!一起加油!