杨校老师课堂备赛C++信奥之模拟算法习题专项训练

杨校2026-01-04 20:24

模拟算法针对性训练

杨校老师课堂备赛C++信奥之模拟算法习题专项训练

【习题】

1. 电梯升降

题目描述

某城市最高的建筑只有一部电梯。一份电梯升降任务表由N个正整数组成，这些数字表示电梯按照给定的顺序停留的楼层号。

电梯升一层花费6秒钟，降一层花费4秒钟，并且每次停留花费5秒钟。

对于每一份任务表，你要计算出完成全部升降任务所花费的总时间。一开始，电梯在第0层，并且最终完成任务时电梯不必一定返回到0层。

输入描述

有多组测试样例。每组测试样例包含一个正整数N，接下来是N个正整数。

在输入中，所有的数字都小于100。当N=0时，表示输入结束。

输出描述

对于每一组测试样例，在一行中输出总时间。

样例

输入

1 2

3 2 3 1

0

输出

17

41

2. 数列

题目描述

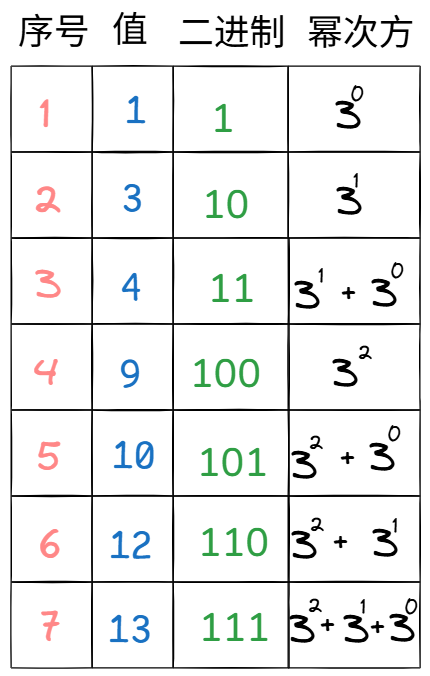
给定一个正整数k(3≤k≤15),把所有k的方幂及所有有限个互不相等的k的方幂之和构成一个递增的序列，例如，当k=3时，这个序列是： 1，3，4，9，10，12，13，... （该序列实际上就是： 3 0 , 3 1 , 3 0 + 3 1 , 3 2 , 3 0 + 3 2 , 3 1 + 3 2 , 3 0 + 3 1 + 3 2 3^0,3^1,3^0+3^1,3^2,3^0+3^2,3^1+3^2,3^0+3^1+3^2 30,31,30+31,32,30+32,31+32,30+31+32...） 请你求出这个序列的第N项的值（用10进制数表示）。 例如，对于k=3，N=100，正确答案应该是981。

输入描述

输入只有1行，为2个正整数，用一个空格隔开： k N（k、N的含义与上述的问题描述一致，且3≤k≤15，10≤N≤1000）。

输出描述

输出为计算结果，是一个正整数。（整数前不要有空格和其他符号）。

样例

输入

3 100

输出

981

3. 扑克洗牌问题

题目描述

给您2n张牌，编号为1,2,3,4,5......n,n+1,......2n，这也是最初牌的顺序。一次洗牌是把序列变为n+1,1,n+2,2,n+3,3......2n,n。可以证明，对于任意自然数n，都可以在经过m次洗牌后重新得到初始的顺序。编程对于小于10000的自然数n（n从键盘输入）的洗牌，求出重新得到初始顺序的洗牌次数m的值，并显示洗牌过程。

输入描述

输入整数n

输出描述

显示洗牌过程，并输出洗牌次数m

样例

输入

5

输出

1 2 3 4 5 6 7 8 9 10

1:6 1 7 2 8 3 9 4 10 5

2:3 6 9 1 4 7 10 2 5 8

3:7 3 10 6 2 9 5 1 8 4

4:9 7 5 3 1 10 8 6 4 2

5:10 9 8 7 6 5 4 3 2 1

6:5 10 4 9 3 8 2 7 1 6

7:8 5 2 10 7 4 1 9 6 3

8:4 8 1 5 9 2 6 10 3 7

9:2 4 6 8 10 1 3 5 7 9

10:1 2 3 4 5 6 7 8 9 10

m=10

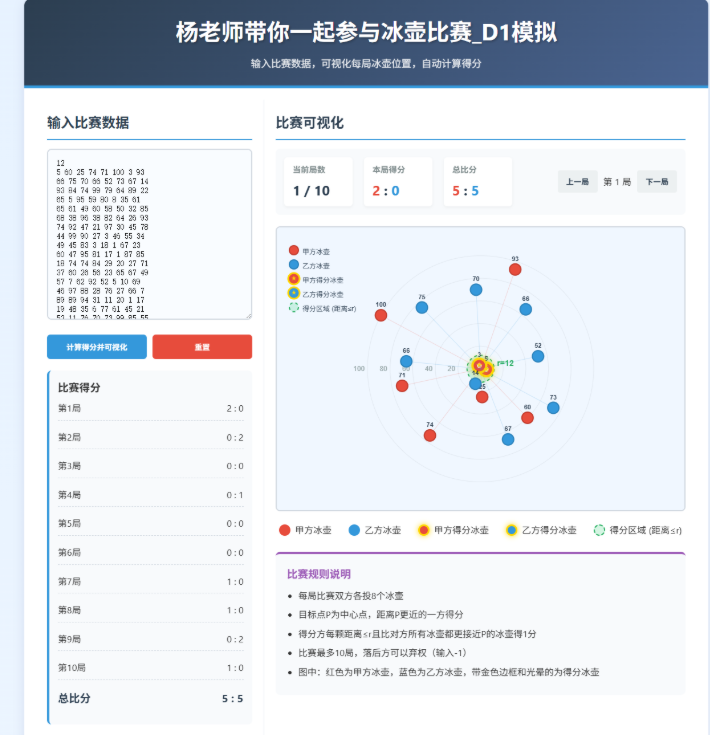
4. 冰壶比赛

题目描述

在冰壶比赛中，给出一个目标点P以及一个规定的正整数r。每一局由甲和乙两队轮流投冰壶各8次后，该局比赛结束。此时，哪一方的冰壶最终离目标点P更近，该方得分，另一方不得分。得分方每颗离目标点P距离小于或等于r、位置较另一队所有冰壶都更接近目标点P的冰壶都可以得1分

比赛最多进行10局。双方之间的某局比赛结束后，落后一方可以弃权。此时，比赛不再进行下去

已知每一局结束时，双方的每个冰壶离目标点P的距离以及正整数r，请写一个程序判断两队之间每一局比赛的得分，以及总得分

输入描述

第一行一个正整数r

以下有若干行（不超过20行），每一行8个正整数（之间用一个空格间隔）

第二行的第j个数表示第一局比赛结束时，甲方的第j个冰壶距离目标点P的距离

第三行的第j个数表示第一局比赛结束时，乙方的第j个冰壶距离目标点P的距离

......

第2k行的第j个数表示第k局比赛结束时，甲方的第j个冰壶距离目标点P的距离

第2k+1行的第j个数表示第k局比赛结束时，乙方的第j个冰壶距离目标点P的距离

如果有一方中途弃权，则最后一行（偶数行）只有一个整数-1，表示此时发生弃权情况

输出描述

输出若干行，每行两个整数，中间以一个冒号间隔，表示每一局比赛甲乙双方的比分（甲得分在前）。最后一行有2个整数，中间以一个冒号间隔，表示甲乙双方比赛的最终得分（甲得分在前）

样例

输入

12

5 60 25 74 71 100 3 93

66 75 70 66 52 73 67 14

93 84 74 99 79 64 89 22

65 5 95 59 80 8 35 61

65 61 49 60 58 50 32 85

68 38 96 38 82 64 26 93

74 92 47 21 97 30 45 78

44 99 90 27 3 46 55 34

49 45 83 3 18 1 67 23

60 47 95 81 17 1 87 85

18 74 74 84 29 20 27 71

37 60 26 56 23 65 67 49

57 7 62 92 52 5 10 69

46 97 88 28 76 27 66 7

89 89 94 31 11 20 1 17

19 48 35 6 77 61 45 21

52 11 76 70 73 99 85 55

90 25 20 7 64 24 94 4

3 43 32 74 10 93 35 77

77 100 63 91 10 73 22 57

输出

2:0

0:2

0:0

0:1

0:0

0:0

1:0

1:0

0:2

1:0

5:5

5. 寻宝

题目描述

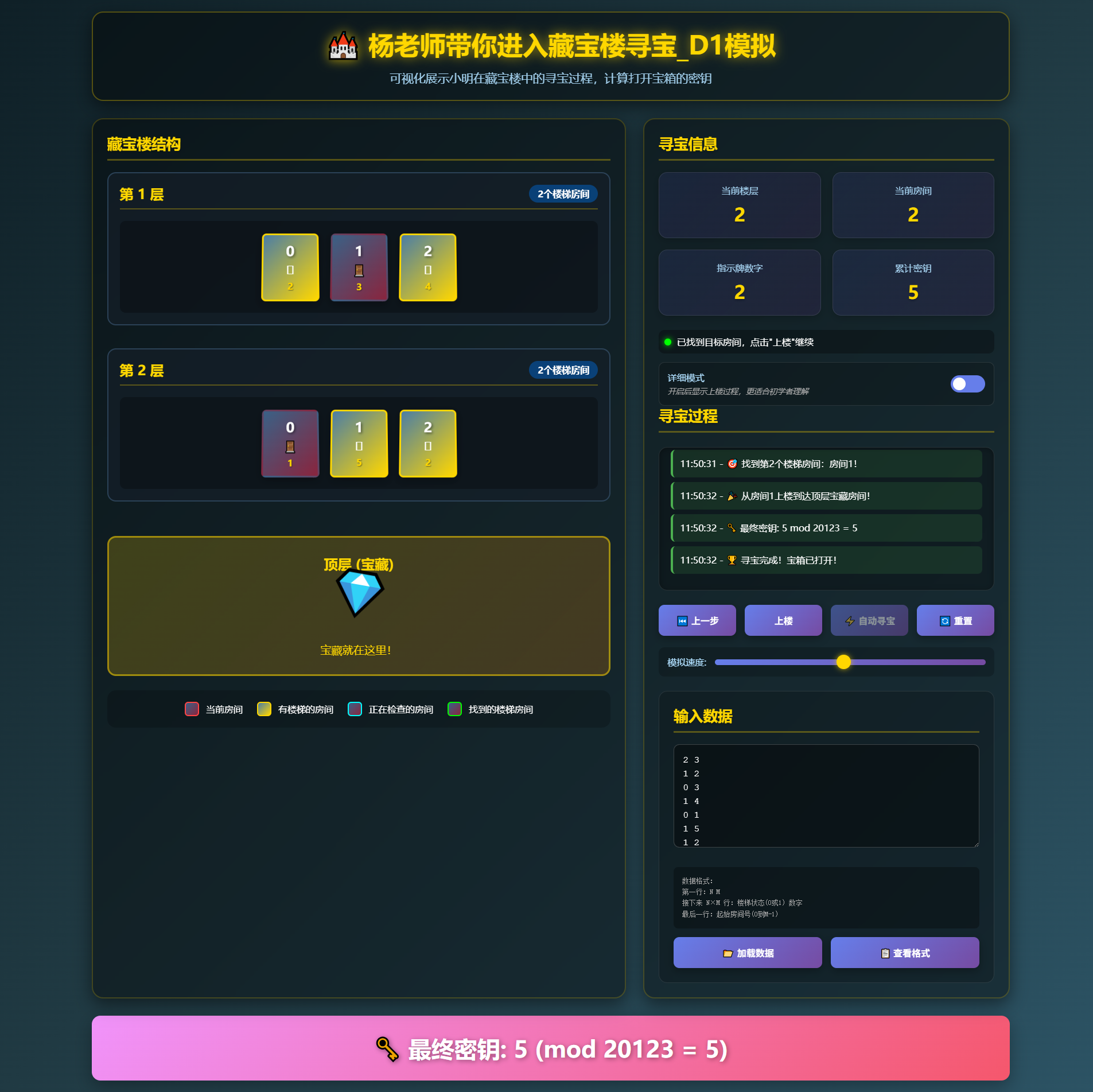
传说很遥远的藏宝楼顶层藏着诱人的宝藏。小明历尽千辛万苦终于找到传说中的这个藏 宝楼，藏宝楼的门口竖着一个木板，上面写有几个大字：寻宝说明书。说明书的内容如下：

藏宝楼共有 N+1 层，最上面一层是顶层，顶层有一个房间里面藏着宝藏。除了顶层外， 藏宝楼另有 N 层，每层 M 个房间，这 M 个房间围成一圈并按逆时针方向依次编号为 0，...， M-1。其中一些房间有通往上一层的楼梯，每层楼的楼梯设计可能不同。每个房间里有一个 指示牌，指示牌上有一个数字 x，表示从这个房间开始按逆时针方向选择第 x 个有楼梯的房 间（假定该房间的编号为 k），从该房间上楼，上楼后到达上一层的 k 号房间。比如当前房 间的指示牌上写着 2，则按逆时针方向开始尝试，找到第 2 个有楼梯的房间，从该房间上楼。 如果当前房间本身就有楼梯通向上层，该房间作为第一个有楼梯的房间。

寻宝说明书的最后用红色大号字体写着："寻宝须知：帮助你找到每层上楼房间的指示 牌上的数字（即每层第一个进入的房间内指示牌上的数字）总和为打开宝箱的密钥"。

请帮助小明算出这个打开宝箱的密钥。

输入描述

第一行 2 个整数 N 和 M，之间用一个空格隔开。N 表示除了顶层外藏宝楼共 N 层楼， M 表示除顶层外每层楼有 M 个房间。

接下来 N*M 行，每行两个整数，之间用一个空格隔开，每行描述一个房间内的情况， 其中第(i-1)*M+j 行表示第 i 层 j-1 号房间的情况（i=1, 2, ..., N；j=1, 2, ... ,M）。

  • 第一个整数 表示该房间是否有楼梯通往上一层（0 表示没有，1 表示有）；
  • 第二个整数表示指示牌上的数字。
    • 注意，从 j 号房间的楼梯爬到上一层到达的房间一定也是 j 号房间。
      最后一行，一个整数，表示小明从藏宝楼底层的几号房间进入开始寻宝（注：房间编号 从 0 开始）。

输出描述

输出只有一行，一个整数，表示打开宝箱的密钥，这个数可能会很大，请输出对 20123 取模的结果即可。

样例

输入

2 3

1 2

0 3

1 4

0 1

1 5

1 2

1

输出

5

提示

【输入输出样例说明】

  • 第一层： 0 号房间，有楼梯通往上层，指示牌上的数字是 2； 1 号房间，无楼梯通往上层，指示牌上的数字是 3； 2 号房间，有楼梯通往上层，指示牌上的数字是 4；
  • 第二层： 0 号房间，无楼梯通往上层，指示牌上的数字是 1； 1 号房间，有楼梯通往上层，指示牌上的数字是 5； 2 号房间，有楼梯通往上层，指示牌上的数字是 2；
  • 小明首先进入第一层（底层）的 1 号房间，记下指示牌上的数字为 3，然后从这个房间 开始，沿逆时针方向选择第 3 个有楼梯的房间 2 号房间进入，上楼后到达第二层的 2 号房间， 记下指示牌上的数字为 2，由于当前房间本身有楼梯通向上层，该房间作为第一个有楼梯的房间。因此，此时沿逆时针方向选择第 2 个有楼梯的房间即为 1 号房间，进入后上楼梯到达顶层。这时把上述记下的指示牌上的数字加起来，即 3+2=5，所以打开宝箱的密钥就是 5。
    【数据范围】 对于 50%数据，有 0<N≤1000，0<x≤10000；对于 100%数据，有 0<N≤10000，0<M≤100，0<x≤1,000,000。

【教学注意点】

一、模拟概念

  • 模拟定义

模拟算法是指严格按照题目描述的规则、流程、逻辑，一步步 "还原" 问题场景并执行计算的算法，核心是 "照章办事"------ 把现实 / 题目中的操作转化为代码中的变量、循环、条件判断等逻辑。

  • 对比枚举算法：枚举是 "穷举所有可能解验证条件"，模拟是 "按规则执行过程求结果"；
  • 核心目标：让代码 "复刻" 题目描述的每一个操作步骤，不跳步、不简化（除非有明确的优化依据）

二、 模拟特征

特征具体说明流程化题目会明确给出 "一步接一步" 的操作规则，代码需按顺序实现；状态跟踪需定义变量跟踪关键状态（如当前楼层、当前房间、当前得分等）；边界处理重点处理环形、取模、特判（如余数为 0、弃权、多组输入结束条件）等边界场景；效率优化对大数据量场景（如 x≤1e6），需在 "忠实模拟" 基础上做数学优化（如取模、预处理）。

【教学过程】

1、回顾

(1) ：回顾一下上节课学习的内容，枚举算法

一、枚举算法的核心定义

枚举算法（也叫穷举算法）是最基础、最直观的算法之一，核心思路是：将问题的所有可能解一一列举出来，逐一验证是否符合题目要求，最终找到符合条件的解（或所有解）。简单来说，枚举就是 "不遗漏、不重复地尝试每一种可能性"，是解决 "答案范围明确、可穷举" 类问题的首选方法。

二、枚举算法的核心特征（上堂课重点）

  1. 明确枚举范围：必须先确定所有可能解的边界（比如 "1~1000 的整数""字符串的所有子串""数组的所有组合"），避免无限枚举或遗漏；
  2. 确定验证条件：对每个枚举的候选解，有清晰的判断规则（比如 "是否是质数""是否满足方程""是否符合题目约束"）；
  3. 优化枚举效率 ：枚举的核心痛点是 "效率低"，上堂课我们重点强调了两类优化：

    1. 剪枝：提前排除不可能符合条件的候选解（比如找 "两数之和为 100" 时，若第一个数 > 100，直接跳过）；

    2. 缩小范围：通过题目约束压缩枚举边界（比如 "三位数的水仙花数"，直接枚举 100~999 即可，无需枚举 0~9999）。

    3. 三、枚举算法的适用场景（上堂课总结）

    4. 上堂课我们明确了枚举算法的适用场景，大家要牢记：

    5. 候选解的数量有限且可明确界定（比如 "1~1000""数组长度≤100"）；

    6. 验证条件简单易实现（无需复杂计算）；

    7. 问题没有更高效的算法（比如无数学规律、无贪心 / 动态规划思路时，枚举是兜底方案）。

2、 授课

  1. 电梯升降问题（多组输入 + 状态计算）
    1. 多组输入处理 ：通过while(cin>>n)+if(n==0) break实现多组测试用例的输入终止；
    2. 状态转移计算 ：用t跟踪当前楼层，根据 "上升 / 下降" 分别计算时间（上升 6 秒 / 层、下降 4 秒 / 层）；
    3. 固定成本累加 ：提前计算所有停留的总时间（sum=n*5），再叠加升降时间；
    4. 逐次更新状态 ：每到一个楼层后即时更新t=k，确保下一次计算的基准正确。
  2. 数列问题（规律模拟 + 进制转换）
    1. 规律转化模拟：将 "k 的方幂组合序列" 转化为 "N 的二进制表示"，用数学规律替代暴力枚举所有组合，是 "智能模拟" 的体现；
    2. 进制转换（十进制→二进制） ：通过短除法将 N 转化为二进制数组a；
    3. 按权展开计算 ：将二进制数组以 k 为基数展开（sum += a[i]*pow(k,i)），得到序列第 N 项；
    4. 数据类型选择 ：用long long存储结果，避免数值溢出（k=15、N=1000 时结果较大）。
  3. 扑克洗牌问题（数组操作 + 循环终止）
    1. 数组复制与重排 ：用两个数组a（原始牌）、b（洗牌后）实现 "n+1,1,n+2,2..." 的洗牌规则，是 "序列重排" 的典型模拟；
    2. 循环终止条件 ：通过标记f判断是否回到初始序列（f=0表示完全一致），避免无限循环；
    3. 过程输出：按要求打印每一轮洗牌后的序列，体现 "模拟过程可视化" 的需求；
    4. 计数统计 ：用m统计洗牌次数，每轮洗牌后递增，直到满足终止条件。
  4. 冰壶比赛问题（多轮流程 + 终止条件）
    1. 多轮流程模拟 ：通过for(int i=1;i<=10;i++)模拟最多 10 局比赛，每局独立计算得分；
    2. 终止条件处理 ：读取第一个数时判断a[0]==-1，触发弃权则立即终止比赛（break）；
    3. 极值查找 ：遍历数组找甲乙两队冰壶的最小距离（min1/min2），是 "找最值" 的基础模拟操作；
    4. 条件计分规则：严格按 "有效距离≤r + 比对方所有冰壶更近" 的条件统计得分，体现 "规则复刻" 的核心；
    5. 总分累加 ：用a1/a2跟踪总得分，每局得分后即时累加
  5. 寻宝问题（环形场景 + 大数优化）
    1. 环形结构处理 ：利用rk = rk % m实现房间编号的环形循环（0→1→2→0），是模拟 "环形场景" 的通用技巧；
    2. 大数取模优化 ：当需要找 "第 x 个有楼梯房间" 且 x 远大于楼梯房间总数时，通过nums = num[i][rk] % cnts[i]+ 余数为 0 的特判（nums == 0时赋值为cnts[i]），避免暴力循环 x 次；
    3. 状态跟踪 ：用rk跟踪当前房间号，key跟踪密钥总和，i跟踪当前楼层，每一层操作后更新状态；
    4. 取模防溢出 ：密钥累加时key=(key+num[i][rk]%20123)%20123，符合 "大数取模" 的编程规范

3、总结

  1. 模拟算法的核心是 "复刻题目规则"，重点关注状态跟踪和流程执行；
  2. 环形场景用%取模、大数场景用取模优化、多轮场景注意终止条件；
  3. 变量语义化、状态即时更新、格式严格匹配，是模拟算法的编程规范；
  4. 对有数学规律的模拟题（如数列），可通过规律转化简化模拟过程，提升效率。

题目一 【电梯升降】--- 例题讲解

直接循环

【电梯运行耗时规则】

  • ①↑上升1层，耗时6秒
  • ② 每层停靠，耗时5秒
  • ③↓下降1层，耗时4秒

【讲解步骤】

1：处理多组输入，判断是否终止

  1. 读取第一个整数n（表示本组任务的停留楼层数量）；
  2. 检查n是否为 0：
    1. 若n=0：结束所有计算，程序终止；
    2. 若n≠0：进入本组任务的计算流程。

2：初始化电梯状态（每组任务独立初始化）

为当前组任务初始化两个核心状态：

  1. 电梯当前楼层：设为 0 层（题目要求初始位置）；
  2. 总耗时：设为 0 秒（每组任务的时间独立计算，需重置）。

3：逐次处理每个目标楼层（核心计算步骤）

对本组的n个目标楼层，依次执行以下操作（共循环n次）：

3.1：读取目标楼层

读取当前要到达的目标楼层号（记为f）。

3.2：计算移动耗时并累加

  1. 计算 "目标楼层 - 当前楼层" 的差值（记为高度差）：
    1. 若高度差 > 0（电梯需要上升）：移动耗时 = 高度差 × 6 秒；
    2. 若高度差 < 0（电梯需要下降）：移动耗时 = 高度差的绝对值 × 4 秒；
    3. 若高度差 = 0（目标楼层 = 当前楼层）：移动耗时 = 0 秒；
  2. 将移动耗时累加到总耗时中。

3.3：累加停留耗时

无论是否移动，到达目标楼层后需停留 5 秒，将 5 秒累加到总耗时中。

3.4：更新电梯当前楼层

将电梯当前楼层更新为刚到达的目标楼层（为下一个楼层的计算做准备）。

4：输出本组总耗时

所有n个目标楼层处理完成后，输出当前组的总耗时。

5：回到步骤 1，处理下一组输入

完成当前组计算后，返回步骤 1，继续读取下一个n，直到读取到n=0为止。

图解题意：

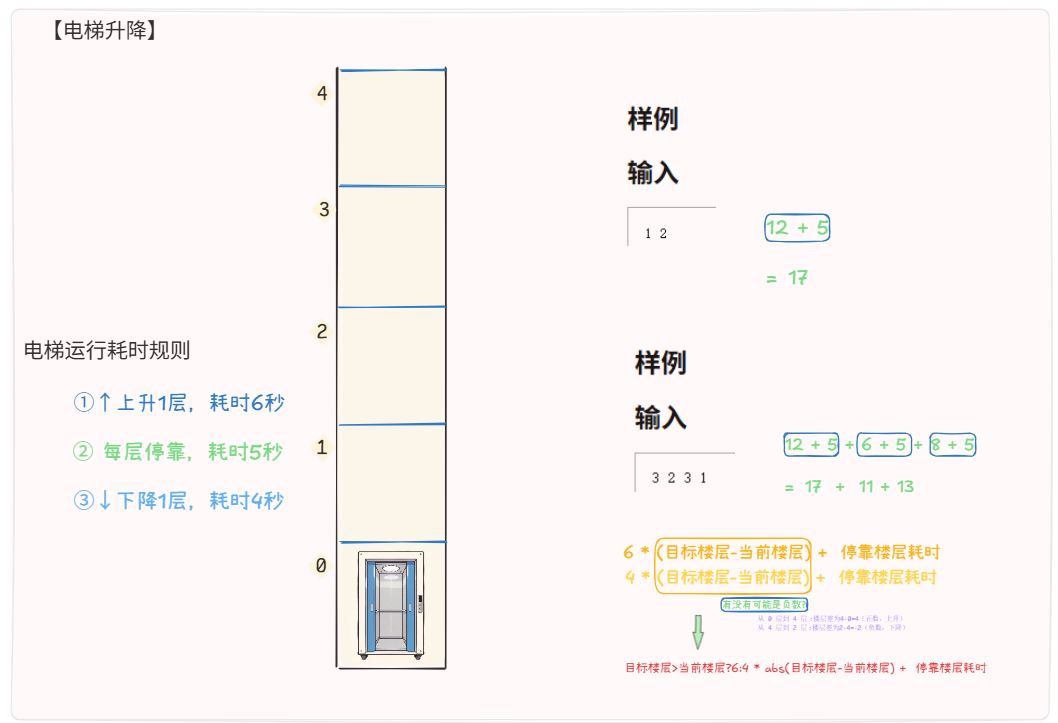
【解题逻辑 】

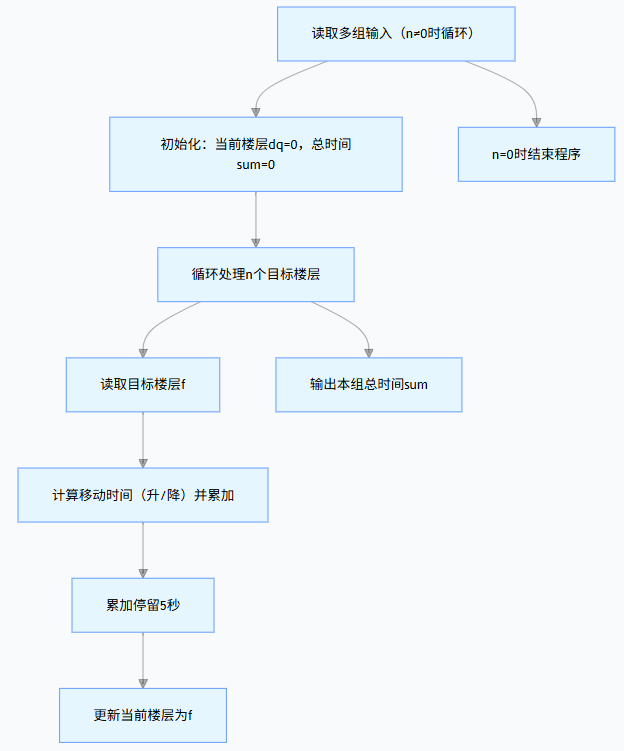
【代码演示】

采用直接循环，代码和效率优于前缀和打表：

C++ 复制代码 
#include <iostream>
using namespace std;

int main() {
    int n;  // 任务数量，表示每组测试样例中有多少个楼层需要停留
    
    // 循环读取多组测试数据，直到遇到n=0时结束输入
    // cin >> n 读取第一个数字（任务数量）
    // && n != 0 检查是否到达输入结束标志（n=0）
    while (cin >> n && n != 0) {
        
        int dq = 0;   // dq：当前电梯所在楼层（当前的拼音首字母）
                      // 初始化为0层，因为题目说明电梯从第0层开始
        
        int sum = 0;  // sum：总时间（秒），用于累加计算完成所有任务的时间
        
        // 循环处理n个楼层任务
        // i从1开始计数，到n结束（包含n），共循环n次
        for (int i = 1; i <= n; i++) {
            
            int f;    // f：目标楼层（floor的简写）
            cin >> f; // 读取一个目标楼层号
            
            // 计算当前楼层与目标楼层之间的高度差
            // 正数表示需要上升，负数表示需要下降
            int cha = f - dq;  // cha：高度差 
            /* 根据高度差计算移动时间
                 使用三元运算符（条件运算符）：
                    ① 如果 cha > 0（上升）：sum增加 cha * 6（上升每层6秒）
                    ② 否则（下降）：sum增加 (-cha) * 4（下降每层4秒，注意-cha取绝对值）
                    ③ 如果cha = 0（目标楼层就是当前楼层），则不增加移动时间
            */
            cha > 0 ? sum += cha * 6 : sum += (-cha) * 4;
            
            // 每次到达目标楼层后，电梯停留5秒（题目要求）
            // 无论是否需要移动，只要完成任务表中的一个停留点，就要加5秒
            sum += 5;
            
            // 更新电梯当前位置，将当前楼层设置为刚刚到达的目标楼层
            // 为计算下一个任务（下一段移动）做准备
            dq = f;
        }
        
        // 输出总时间
        cout << sum << endl;
    }
    return 0;
}

解法二

  1. 初始化设置：确定电梯初始位置在 0 层，准备一个变量记录总时间（初始为 0）。
  2. 循环处理多组测试数据 ：
    1. 读取每组测试数据的楼层数量 n，当 n=0 时结束程序。
    2. 对于每组数据，依次读取每个目标楼层号。
  3. 计算每次移动的时间 ：
    1. 计算当前楼层到目标楼层的距离（楼层差的绝对值）。
    2. 根据方向计算移动时间：上升时每层 6 秒，下降时每层 4 秒。
    3. 加上在目标楼层的停留时间 5 秒，将结果累加到总时间中。
    4. 更新当前楼层为刚到达的楼层，为下一次移动做准备。
  4. 输出结果：每组测试数据处理完成后，输出总时间。
C++ 复制代码 
#include <iostream>
#include <cmath>  // 需要包含cmath头文件使用abs()函数
using namespace std;
int main() {
    int n;  // 任务数量
    while (cin >> n && n != 0) {  // 循环读取多组数据
        int sum = 0;    // 总时间
        int dq = 0;     // 前一个楼层，初始为0层
        for (int i = 0; i < n; i++) {  // 处理n个任务
            int f;      // 当前目标楼层
            cin >> f;   // 读取目标楼层  
            // 核心计算：一行代码完成所有计算
                //  计算两个楼层的距离（层数差）
                // （目标楼层 > 当前楼层），说明是上升，返回6（上升速度），否则返回4（下降速度）+ 每次停留的固定时间5秒
            sum += abs(f - dq) * (f > dq ? 6 : 4) + 5;    
            dq = f;  // 更新前一个楼层
        }
        cout << sum << endl;  // 输出结果
    }
    return 0;
}

题目二【数列】

【题意解析】

  1. 给定一个正整数 k（3≤k≤15）
  2. 我们要生成一个递增序列，这个序列包含：
    1. 所有 k 的方幂（即 k⁰, k¹, k², k³...，其中 k⁰=1）
    2. 所有由互不相等的 k 的方幂相加得到的和（如 k⁰+k¹, k⁰+k², k¹+k², k⁰+k¹+k² 等）
  3. 需要求出这个序列中的第 N 项（注意序列是从第 1 项开始计数的）

【图解找规律】

本题类似"0/1背包思想"

\1. 物品：k的幂（k⁰, k¹, k², ...）

\2. 价值：每个幂本身就是价值

\3. 限制**：每个物品要么选（1），要么不选（0）**

\4. 目标：不是求最大价值，而是按特定顺序排列所有可能的组合


【代码实现】

  • 时间复杂度在 O(n²)

第一步：先明确 "k=3，N=4" 要找什么

题目要求：找由 "3 的方幂" 和 "互不相等的 3 的方幂之和" 组成的递增序列的第 4 项。先手动列出 k=3 的序列，确认第 4 项是什么（先有直观认知）：

  • 3 的方幂：3⁰=1、3¹=3、3²=9、3³=27......
  • 互不相等的方幂之和：3⁰+3¹=4、3⁰+3²=10、3¹+3²=12......
  • 按递增排序的序列：第 1 项 = 1，第 2 项 = 3，第 3 项 = 4，第 4 项 = 9。

我们的目标就是通过 "二进制规律"，不用枚举序列，直接算出第 4 项 = 9。

第二步：把 N=4 转化为二进制（核心关键）

先回忆：十进制转二进制的方法是 "除 2 取余，逆序排列"。对 N=4 做转换：

  1. 4 ÷ 2 = 2，余 0；
  2. 2 ÷ 2 = 1，余 0；
  3. 1 ÷ 2 = 0，余 1；
  4. 逆序排列余数：1 0 0 → 所以 4 的二进制是100。

第三步：二进制和 "3 的方幂" 的对应规则

规则：把二进制数从右往左数 （从 0 开始数位数），"1" 出现在第几位，就取 3 的几次方；如果是 0，就不取。对二进制100分析：

二进制位(从右数) 2 1 0

二进制值 1 0 0

是否取3的对应方幂 取 不取 不取

对应的3的方幂 3² - -

第四步：计算最终结果

把 "取" 的方幂加起来（这里只有一个 3²）：

3² = 9 → 这就是序列的第 4 项，和我们手动枚举的结果一致！

再拆解 "逐位计算" 的过程（模拟代码执行逻辑）

如果用代码的思路一步步算，过程是这样的：

  1. 初始化：结果result=0，当前 3 的方幂power=3⁰=1（从最低位开始），N=4；
  2. 第一次循环（处理二进制最低位）：
    1. N=4，二进制最低位是 0（4&1=0）→ 不取当前 power（1）；
    2. power 更新为 3¹=3；
    3. N 右移一位（去掉最低位）→ N=2；
  3. 第二次循环（处理第二位）：
    1. N=2，二进制最低位是 0（2&1=0）→ 不取当前 power（3）；
    2. power 更新为 3²=9；
    3. N 右移一位→ N=1；
  4. 第三次循环（处理第三位）：
    1. N=1，二进制最低位是 1（1&1=1）→ 取当前 power（9），result=0+9=9；
    2. power 更新为 3³=27；
    3. N 右移一位→ N=0（循环结束）；
  5. 最终 result=9，就是第 4 项的值。

总结（针对 k=3，N=4 的核心）

  1. N=4 的二进制是 100，只有第 2 位是 1；
  2. 对应取 3 的 2 次方，结果就是 9；
  3. 这个思路的本质是：把 "找序列第 N 项" 转化为 "N 的二进制位对应 k 的方幂求和"，不用枚举所有项，直接计算，效率极高。
C++ 复制代码 
#include <iostream>
using namespace std;

int main() {
    int k, N;
    cin >> k >> N;
    
    int result = 0;
    int power = 1;  // k的幂
    
    // 将N转换为二进制，每一位对应一个k的幂
    while (N > 0) {
        if (N & 1) {  // 如果N的二进制最低位是1
            result += power;
        }
        power *= k;  // k的幂递增：k^0, k^1, k^2, ...
        N >>= 1;     // N右移一位，处理下一位二进制
    }
    
    cout << result << endl;
    return 0;
}

题目三 【扑克洗牌问题】

图解：

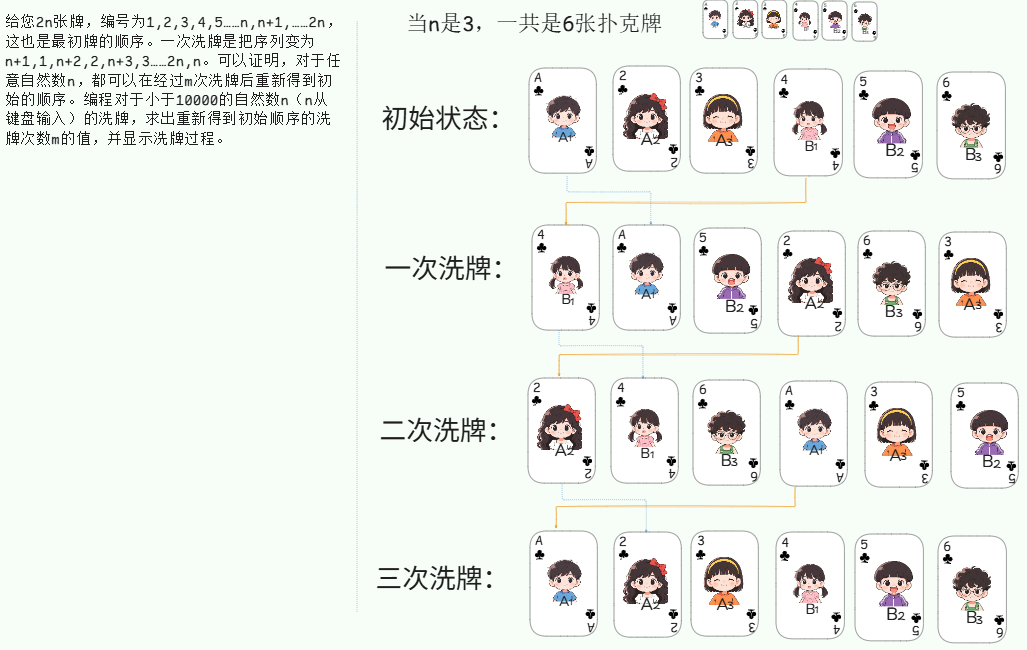
【讲解步骤】

1：输入处理与初始化

  1. 读取输入的正整数n（表示 "2n 张牌" 中的 n）；
  2. 计算总牌数N=2×n（比如 n=5 时，N=10）；
  3. 初始化牌序列：按1,2,3,...,N的顺序构建初始牌序（下标从 1 开始，方便对应牌的位置）；
  4. 输出初始牌序（这是洗牌前的基准序列）；
  5. 初始化洗牌次数计数器m=0（尚未开始洗牌）。

2：循环执行洗牌操作

进入无限循环（直到恢复初始顺序为止），每次循环执行一次完整洗牌：

2.1：更新洗牌次数并标记

  1. 洗牌次数m加 1（表示本次是第 m 次洗牌）；
  2. 输出 "m:"（标记当前是第几次洗牌的结果）。

2.2：备份当前牌序

复制一份当前的牌序作为 "原始牌序备份"（因为洗牌需要基于洗牌前的顺序计算，不能直接覆盖）。

2.3：执行一次洗牌（按规则重排）

遍历前 n 张牌的位置（i 从 1 到 n），按以下规则更新牌序：

  1. 新牌序的奇数位置 （第 1、3、5... 位）：放入原始备份中 "后 n 张牌" 的第 i 张（即原始备份的 n+i 位置）；
    1. 举例（n=3，i=1）：新牌序第 1 位（2×1-1=1）= 原始备份第 4 位（3+1=4）；
    2. 举例（n=3，i=2）：新牌序第 3 位（2×2-1=3）= 原始备份第 5 位（3+2=5）；
  2. 新牌序的偶数位置 （第 2、4、6... 位）：放入原始备份中 "前 n 张牌" 的第 i 张（即原始备份的 i 位置）；
    1. 举例（n=3，i=1）：新牌序第 2 位（2×1=2）= 原始备份第 1 位；
    2. 举例（n=3，i=2）：新牌序第 4 位（2×2=4）= 原始备份第 2 位。

2.4：输出本次洗牌后的牌序

按顺序输出本次洗牌后的所有牌（数字间用空格分隔，最后一个数字后换行）。

3：检查是否恢复初始顺序

  1. 初始化标志位flag=0（0 表示 "已恢复初始顺序"，1 表示 "未恢复"）；
  2. 遍历所有牌的位置（i 从 1 到 N）：
    1. 检查当前位置 i 的牌是否等于 i（即 "位置 1 是 1、位置 2 是 2... 位置 N 是 N"）；
    2. 如果发现任意一个位置不匹配，将flag设为 1（标记未恢复）；
    3. 注意：即使发现不匹配，仍需遍历完所有位置（保证牌序输出完整）。

4：判断是否终止循环

  1. 如果flag=0（所有位置都匹配，恢复初始顺序）：
    1. 输出 "m=xx"（xx 为最终的洗牌次数）；
    2. 退出循环，结束程序；
  2. 如果flag=1（未恢复）：回到步骤 2，继续下一次洗牌。
C++ 复制代码 
#include <iostream>
#include <vector> 
using namespace std;

int main(){
    int n;  // 输入n，表示有2n张牌
    cin >> n; // 例如输入3，表示有6张牌
    
    int N = 2 * n;  // 总牌数，例如n=3时，N=6
    
    // 创建数组vec存储当前牌的顺序，使用N+1是为了让下标从1开始使用
    vector<int> vec(N+1);
    
    // 初始化：按照1,2,3,...,2n的顺序排列
    // 同时输出初始牌序
    for(int i = 1; i <= N; i++){
        vec[i] = i;  // 第i个位置放数字i
        // 输出：最后一个数字后换行，其他数字后加空格
        cout << i << (i == N ? "\n" : " ");
    }
    
    int m = 0;  // 洗牌次数计数器，初始为0
    
    // 无限循环洗牌，直到恢复初始顺序
    while(1){
        m++;  // 洗牌次数加1
        cout << m << ":";  // 输出当前是第几次洗牌
        
        // 创建一个临时数组t，复制当前vec的牌序
        // 我们需要用原来的顺序来计算新的顺序
        vector<int> t(vec);
        
        // 执行一次洗牌操作
        // i从1遍历到n（前一半牌的数量）
        for(int i = 1; i <= n; i++){ 
            // 洗牌规则：新顺序的奇数位置放原来的后一半牌
            // vec[2*i-1] 对应新顺序的第1,3,5,...个位置（奇数位置）
            // t[n + i] 对应原来顺序的第n+1, n+2, ..., 2n张牌（后一半牌）
            vec[2*i-1] = t[n + i]; // 例如：vec[1] = t[4]（当n=3,i=1时）
            
            // 洗牌规则：新顺序的偶数位置放原来的前一半牌
            // vec[2*i] 对应新顺序的第2,4,6,...个位置（偶数位置）
            // t[i] 对应原来顺序的第1,2,...,n张牌（前一半牌）
            vec[2*i] = t[i]; // 例如：vec[2] = t[1]（当n=3,i=1时）
        }
        
        // 检查是否恢复到了初始顺序
        int flag = 0;  // 标志位：0表示已恢复，1表示未恢复
        
        // 遍历所有位置，输出当前顺序并检查是否恢复
        for(int i = 1; i <= N; i++){ 
            // 输出当前第i个位置的数字
            cout << vec[i] << (i == N ? "\n" : " ");
            
            // 检查这个位置是否恢复：当前位置的数字应该等于这个位置的编号
            // 例如：位置1应该放数字1，位置2应该放数字2，以此类推
            // 如果发现不匹配，设置flag=1表示还未恢复
            if(vec[i] != i){ 
                flag = 1;
                // 注意：这里没有break，即使发现未恢复，也继续输出全部
                // 可以考虑加break提前结束检查以提高效率
            } 
        } 
        
        // 如果flag保持为0，说明所有位置都匹配，已经恢复初始顺序
        if(flag == 0){
            cout << "m=" << m;  // 输出总共需要的洗牌次数
            break;  // 退出循环
        }
        // 如果flag=1，继续下一次洗牌
    }
    
    return 0;
}

题目四 【冰壶比赛】

【图解题目】

【讲解步骤】

1：初始化基础数据

  1. 读取有效半径r（冰壶需≤r 才有效）；
  2. 初始化甲乙两队总得分zfA=0、zfB=0（用于累加所有局的得分）；
  3. 开始循环处理最多 10 局比赛（局数j从 1 到 10）。

2：读取单局比赛数据（核心输入环节）

  1. 先读取甲队第一个冰壶的距离：
    1. 若该值为 - 1：表示有队伍弃权，直接跳出所有局的循环，结束比赛；
    2. 若不为 - 1：继续读取甲队剩余 7 个冰壶的距离（共 8 个），存入数组A[1~8]；
  2. 读取乙队全部 8 个冰壶的距离，存入数组B[1~8]。

3：计算两队单局最近冰壶距离

  1. 初始化甲队最近距离minA = A[1]，乙队最近距离minB = B[1]；
  2. 遍历甲乙两队剩余 7 个冰壶（下标 2~8）：
    1. 若甲队当前冰壶距离< minA，更新minA为该值；
    2. 若乙队当前冰壶距离< minB，更新minB为该值；（最终minA是甲队最接近靶心的距离，minB是乙队最接近靶心的距离）

4：判定单局胜负并计算得分

  1. 初始化本局甲乙得分dfA=0、dfB=0；
  2. 分情况判定：
    1. 情况 1：甲队获胜（minA < minB） ：遍历甲队 8 个冰壶，对每个冰壶距离A[i]：若A[i] ≤ r（有效）且A[i] < minB（比乙队最近壶更近），则dfA += 1；
    2. 情况 2：乙队获胜（minB < minA） ：遍历乙队 8 个冰壶，对每个冰壶距离B[i]：若B[i] ≤ r（有效）且B[i] < minA（比甲队最近壶更近），则dfB += 1；
    3. 情况 3：平局（minA == minB） ：不做任何操作，dfA和dfB保持 0。

5：输出单局比分并累加总得分

  1. 输出本局比分：dfA:dfB；
  2. 将本局得分累加到总得分：zfA += dfA、zfB += dfB；
  3. 回到步骤 2，处理下一局（直到 10 局结束或读取到 - 1）。

6：输出最终总比分

所有局处理完成后，输出甲乙两队总得分：zfA:zfB

【伪代码梳理】

逻辑流程图

开始

↓

读取半径 r

↓

初始化总得分 zfA=0, zfB=0

↓

循环 j=1 到 10（最多10局）:

├─ 读取甲队第一个距离 A[1]

├─ 如果 A[1] == -1: 退出循环（弃权）

├─ 否则:

│ ├─ 读取甲队剩余7个距离 A[2...8]

│ ├─ 读取乙队8个距离 B[1...8]

│ ├─ 找 minA = 甲队最小距离

│ ├─ 找 minB = 乙队最小距离

│ ├─ 初始化本局得分 dfA=0, dfB=0

│ ├─ 如果 minA < minB:

│ │ 遍历甲队8个壶:

│ │ 如果 壶≤r 且 壶<minB: dfA++

│ ├─ 如果 minB < minA:

│ │ 遍历乙队8个壶:

│ │ 如果 壶≤r 且 壶<minA: dfB++

│ ├─ 输出 dfA:dfB（本局比分）

│ └─ 累加: zfA+=dfA, zfB+=dfB

↓

输出 zfA:zfB（总比分）

↓

结束

【代码】

C++ 复制代码 
#include <iostream>
using namespace std;

int main() {
    //  r 存储有效距离半径
    int r;
    cin >> r;  // 读取半径 r 值
    
    // zfA 存储甲队总得分，zfB 存储乙队总得分
    int zfA = 0, zfB = 0;
    
    // 循环处理最多10局比赛（j 表示当前局数）
    for (int j = 1; j <= 10; j++) {
        // 定义数组 A 存储甲队8个冰壶距离，B 存储乙队8个冰壶距离
        // 注意：数组大小为10，但实际只使用下标1-8，下标0和9未使用
        int A[10], B[10];
        
        // 先读取甲队第一个冰壶距离到 A[1]
        cin >> A[1];
        // 判断是否弃权：如果读取到-1，表示有队伍弃权，结束比赛
        if (A[1] == -1) break;  // 弃权情况
        
        // 读取甲队剩余7个冰壶距离（存储到 A[2] 到 A[8]）
        for (int i = 2; i <= 8; i++) cin >> A[i];
        
        // 读取乙队全部8个冰壶距离（存储到 B[1] 到 B[8]）
        for (int i = 1; i <= 8; i++) cin >> B[i];
        
        // 初始化甲队最近距离为第一个冰壶距离 A[1]
        int minA = A[1];
        // 初始化乙队最近距离为第一个冰壶距离 B[1]
        int minB = B[1];
        
        // 遍历甲队和乙队的冰壶，找出各自的最短距离
        for (int i = 2; i <= 8; i++) {
            // 如果甲队当前冰壶距离比记录的最小值更小，更新 minA
            if (A[i] < minA) minA = A[i];
            // 如果乙队当前冰壶距离比记录的最小值更小，更新 minB
            if (B[i] < minB) minB = B[i];
        }
        
        // dfA 存储本局甲队得分，dfB 存储本局乙队得分
        int dfA = 0, dfB = 0;
        
        // 判断胜负：比较双方最近冰壶的距离
        if (minA < minB) {
            // 甲队获胜（甲队最近壶比乙队最近壶更接近靶心）
            // 遍历甲队所有冰壶，统计得分壶数量
            for (int i = 1; i <= 8; i++) {
                // 得分条件：
                // 1. 冰壶距离 ≤ 有效半径 r
                // 2. 冰壶距离 < 乙队最近距离 minB
                if (A[i] <= r && A[i] < minB) {
                    dfA++;  // 甲队得分加1
                }
            }
        } else if (minB < minA) {
            // 乙队获胜（乙队最近壶比甲队最近壶更接近靶心）
            // 遍历乙队所有冰壶，统计得分壶数量
            for (int i = 1; i <= 8; i++) {
                // 得分条件：
                // 1. 冰壶距离 ≤ 有效半径 r
                // 2. 冰壶距离 < 甲队最近距离 minA
                if (B[i] <= r && B[i] < minA) {
                    dfB++;  // 乙队得分加1
                }
            }
        }
        // 输出本局比分，格式为"甲队得分:乙队得分"
        cout << dfA << ":" << dfB << endl;
        
        // 将本局得分累加到总得分中
        zfA += dfA;  // 甲队总得分增加
        zfB += dfB;  // 乙队总得分增加
    }
    
    // 输出最终总比分，格式为"甲队总得分:乙队总得分"
    cout << zfA << ":" << zfB << endl;
    
    return 0;  
}

题目五 【寻宝】

【题意解析】

一、场景

关键信息具体内容重要性 / 作用楼层结构1. 总层数 = N+1 层（N 层普通楼层 + 1 层顶层）；

\2. 普通楼层：每层 M 个房间，围成环形，编号 0~M-1；

\3. 顶层：只有 1 个房间（无需处理）。定义了核心场景，环形是 "逆时针计数" 的基础房间属性每个普通房间有两个固定属性：1. 楼梯标记（0 = 无楼梯上楼，1 = 有楼梯上楼）；2. 指示牌数字 x（核心计算值）。楼梯标记是 "筛选计数对象" 的依据，x 是 "计数次数"上楼规则从某层 k 号房间的楼梯上楼，必然到达上一层的 k 号房间连接上下层的核心规则，决定下一层的初始房间号

二、规则

关键信息具体内容重要性 / 作用密钥计算对象每层第一个进入的房间的指示牌数字之和

（不管该房间有没有楼梯）。明确 "要累加的数字" 是什么，样例中第一层初始房间 1 号（无楼梯）的数字 3 仍需累加逆时针计数规则1. 计数起点：当前层的 "初始房间"；

\2. 计数范围：仅统计有楼梯的房间；

\3. 计数方式：

  • 若初始房间有楼梯，它算 "第 1 个"；

  • 若初始房间无楼梯，跳过，继续逆时针找，直到数够 x 个；

\4. 环形补充：数到 M-1 号后，下一个是 0 号。这是整个题目的核心逻辑，决定 "上楼房间" 的查找方式上楼房间的作用找到的 "第 x 个有楼梯的房间" 是 "上楼房间"，从这里上楼到上一层同编号房间，该房间成为上一层的 "初始房间"。连接每层的关键，是逐层模拟的核心步骤

【图解】

【代码】

1：数据存储与初始化

  • 定义三个核心数组：
    • lt[i][j]：记录第 i 层第 j 号房间是否有楼梯（1 = 有，0 = 无）；
    • zsp[i][j]：记录第 i 层第 j 号房间的指示牌数字；
    • lt_cnt[i]：预处理每层有楼梯的房间总数（避免重复统计，优化效率）。
  • 读取输入：按 "层→房间" 的顺序读取每个房间的楼梯状态和指示牌数字，并统计每层楼梯数。

2：初始化核心状态

  • key：存储密钥总和，初始为 0；
  • current：存储当前所在房间号，初始为输入的底层入口房间号。

3：逐楼层模拟（核心循环）

对每一层执行以下操作：

  1. 累加密钥 ：将当前楼层初始房间的指示牌数字加到key中，且每次累加后对 20123 取模（避免数值溢出，符合题目要求）；
  2. 优化目标计数 ：
    1. 指示牌数字x可能很大（≤1e6），而每层楼梯数lt_cnt[i]最多 100，因此用x % lt_cnt[i]简化计数（例如 x=100、楼梯数 = 99 时，等价于找第 1 个）；
    2. 特判：若取模结果为 0，说明 x 是楼梯数的整数倍，需找第lt_cnt[i]个（例如 x=99、楼梯数 = 99 时，找第 99 个）；
  3. 逆时针找目标房间 ：
    1. 从当前房间current开始，逐个遍历房间（环形处理：pos = (pos + 1) % M）；
    2. 每遇到一个有楼梯的房间，计数cnt加 1；
    3. 当cnt等于目标数target时，记录该房间号为current（作为下一层的初始房间），结束当前层的查找。

4：输出结果

所有楼层处理完毕后，输出最终的密钥key。

先搞懂代码里的 "核心变量"（先认清楚 "工具"）

变量名通俗解释例子（对应样例输入）N除顶层外的楼层总数样例中 N=2（第一层、第二层）M每层的房间数样例中 M=3（0、1、2 号房间）lt[i][j]第 i 层第 j 号房间有没有楼梯（1 = 有，0 = 无）样例第一层（i=0）：lt [0][0]=1（0 号有楼梯）、lt [0][1]=0（1 号无）、lt [0][2]=1（2 号有）zsp[i][j]第 i 层第 j 号房间指示牌的数字样例第一层 1 号房间：zsp [0][1]=3lt_cnt[i]第 i 层有楼梯的房间总数样例第一层 lt_cnt [0]=2（0、2 号有楼梯）k小明初始进入的房间号样例中 k=1（第一层 1 号房间）key密钥总和（最终要输出的数）样例中 key=3+2=5current当前所在的房间号（动态变化）初始是 1，第一层处理完变成 2，第二层处理完变成 1x当前房间指示牌的数字第一层 current=1 时，x=3target要找的 "第几个有楼梯的房间"（优化后的值）第一层 x=3，lt_cnt [0]=2 → target=3%2=1（余数不为 0）；若 x=4，target=4%2=0 → 修正为 2cnt临时计数器（数找到的有楼梯房间数）找 target=1 时，找到 1 个就停pos遍历房间的临时位置（逆时针走）从 current=1 开始，pos 依次是 1→2→0→1...MOD取模的数（题目要求结果对 20123 取模）累加时每次 %20123，避免数字太大

逐段拆解代码（跟着样例走，一步一步来）

Java 复制代码 
#include <iostream>
using namespace std;

const int MOD = 20123;  // 题目要求结果对20123取模

int main() {
    int N, M;
    cin >> N >> M;  // N：普通楼层数；M：每层房间数
    
    // lt[i][j]：第i层第j号房间是否有楼梯（1=有，0=无），数组维度留冗余避免越界
    int lt[10005][105] = {0};  // 楼梯
    // zsp[i][j]：第i层第j号房间的指示牌数字
    int zsp[10005][105] = {0}; // 指示牌
    // lt_cnt[i]：第i层有楼梯的房间总数
    int lt_cnt[10005] = {0};  // 楼梯计数器   
    
    // 读取N层、每层M个房间的信息
    for (int i = 0; i < N; i++) {
        for (int j = 0; j < M; j++) {
            cin >> lt[i][j] >> zsp[i][j];
            // 统计每层楼梯数：有楼梯则计数+1
            lt_cnt[i] += lt[i][j];
        }
    }
    
    int k;
    cin >> k;  // 底层（第0层）初始进入的房间号
    
    int key = 0;    // 最终的密钥（所有初始房间指示牌数字之和）
    int current = k;  // 当前所在的房间号，初始为底层入口房间
    
    // 逐楼层处理：从第0层到第N-1层（共N层）
    for (int i = 0; i < N; i++) {
        // 1. 累加当前楼层初始房间的指示牌数字（密钥核心）
        int x = zsp[i][current];
        key = (key + x) % MOD;  // 每次累加后取模，避免溢出
        
        // 2. 计算需要找的"第target个有楼梯的房间"（优化大数x）
        // 若x远大于楼梯总数，取模后等价于找第target个（余数为0时取楼梯总数）
        int target = x % lt_cnt[i];
        if (target == 0) target = lt_cnt[i];
        
        // 3. 从当前房间开始，逆时针找第target个有楼梯的房间
        int cnt = 0;   // 已找到的有楼梯房间数
        int pos = current;  // 遍历的当前位置，初始为当前房间
        while (cnt < target) {
            // 找到一个有楼梯的房间，计数+1
            if (lt[i][pos] == 1) cnt++;
            // 找到第target个，更新current并退出循环
            if (cnt == target) {
                current = pos;
                break;
            }
            // 逆时针移动到下一个房间（环形处理：取模M）
            pos = (pos + 1) % M;
        }
    }
    
    // 输出最终密钥（已取模）
    cout << key << endl;
    return 0;
}

逐段拆解代码（跟着样例走，一步一步来）

我们结合样例输入（N=2，M=3；第一层：1 2 / 0 3 / 1 4；第二层：0 1 / 1 5 / 1 2；初始房间 k=1）来拆解：

第一步：读取基础参数 + 存储房间信息
Java 复制代码 
int N, M;
cin >> N >> M;  // 样例中读入N=2，M=3

int lt[10005][105] = {0};  // 存每个房间有没有楼梯
int zsp[10005][105] = {0}; // 存每个房间的指示牌数字
int lt_cnt[10005] = {0};   // 存每层有多少个楼梯房间

// 读取N层、每层M个房间的信息
for (int i = 0; i < N; i++) {  // i=0是第一层，i=1是第二层
    for (int j = 0; j < M; j++) {  // j=0/1/2对应房间号
        cin >> lt[i][j] >> zsp[i][j];  // 读楼梯状态+指示牌数字
        lt_cnt[i] += lt[i][j];  // 统计每层楼梯数
    }
}
  • 处理第一层（i=0）：
    • j=0：读 lt [0][0]=1，zsp [0][0]=2 → lt_cnt [0] +=1 → lt_cnt [0]=1；
    • j=1：读 lt [0][1]=0，zsp [0][1]=3 → lt_cnt [0] +=0 → 还是 1；
    • j=2：读 lt [0][2]=1，zsp [0][2]=4 → lt_cnt [0] +=1 → lt_cnt [0]=2；
  • 处理第二层（i=1）：
    • j=0：lt[1][0]=0，zsp[1][0]=1 → lt_cnt[1]=0；
    • j=1：lt[1][1]=1，zsp[1][1]=5 → lt_cnt[1]=1；
    • j=2：lt[1][2]=1，zsp[1][2]=2 → lt_cnt[1]=2；
  • 最后读 k=1（初始房间是第一层 1 号）。
第二步：初始化密钥和当前房间
C++ 复制代码 
int key = 0;    // 密钥初始为0
int current = k;  // current=1（第一层1号房间）
第三步：逐层处理（核心循环，先处理第一层 i=0）
Java 复制代码 
for (int i = 0; i < N; i++) {  // 先处理i=0（第一层），再处理i=1（第二层）
    // 1. 累加当前房间的指示牌数字到密钥
    int x = zsp[i][current];  // i=0，current=1 → x=3
    key = (key + x) % MOD;    // key=0+3=3（%20123还是3）

    // 2. 计算要找的"第target个楼梯房间"（优化大数）
    int target = x % lt_cnt[i];  // x=3，lt_cnt[0]=2 → 3%2=1
    if (target == 0) target = lt_cnt[i];  // 这里target≠0，不用改

    // 3. 从current=1开始，逆时针找第1个有楼梯的房间
    int cnt = 0;   // 数找到的楼梯房间数，初始0
    int pos = current;  // pos=1（从1号房间开始找）
    while (cnt < target) {  // 只要cnt<1，就继续找
        if (lt[i][pos] == 1) cnt++;  // 检查pos房间有没有楼梯
        if (cnt == target) {  // 找到第1个了
            current = pos;    // 更新current为这个房间号
            break;            // 停止找
        }
        pos = (pos + 1) % M;  // 逆时针走下一个房间（取模保证环形）
    }
}

第一层（i=0）的查找过程：

  • pos=1 → lt [0][1]=0 → cnt 还是 0 → pos=(1+1)%3=2；
  • pos=2 → lt [0][2]=1 → cnt=1（达到 target=1）→ current=2 → 退出循环；→ 第一层处理完：key=3，current=2（下一层从第二层 2 号房间开始）。

第二层（i=1）的处理过程：

C++ 复制代码 
// i=1（第二层），current=2
int x = zsp[1][2];  // zsp[1][2]=2 → x=2
key = (3 + 2) % 20123;  // key=5

int target = 2 % lt_cnt[1];  // lt_cnt[1]=2 → 2%2=0 → 修正为2
// 开始找第2个有楼梯的房间，pos=2
cnt=0，pos=2：
- pos=2 → lt[1][2]=1 → cnt=1 → 没到2 → pos=(2+1)%3=0；
- pos=0 → lt[1][0]=0 → cnt还是1 → pos=(0+1)%3=1；
- pos=1 → lt[1][1]=1 → cnt=2（达到target=2）→ current=1 → 退出循环；

→ 第二层处理完：key=5，current=1（但已经处理完所有楼层，循环结束）。

第四步：输出结果
C++ 复制代码 
cout << key << endl;  // 输出5（和样例一致）

关键难点解释（为什么要这么写？）

  1. 为什么要取模（%）？
    1. 对 key 取模：题目要求结果对 20123 取模，且指示牌数字可能很大，累加后会溢出，所以每次加完都取模；
    2. 对 target 取模：比如指示牌数字 x=1000000，而每层只有 2 个楼梯房间，找第 1000000 个和找第 0 个（修正为 2 个）是一样的，不用真的数 1000000 次，节省时间；
    3. 对 pos 取模：房间是环形的（0→1→2→0），pos=(pos+1)% M 能保证不会超出 0~M-1 的范围。
  2. **为什么要统计 lt_cnt [i]？**提前数好每层有多少个楼梯房间，避免每次找的时候都重新数，节省时间（比如每层 100 个房间，不用每次都遍历 100 次）。
  3. **查找房间的逻辑为什么这么写？**从当前房间开始，逐个逆时针找，每遇到一个有楼梯的房间就计数，直到数到目标数 ------ 完全贴合题目里 "从当前房间开始逆时针选第 x 个有楼梯的房间" 的规则。

总结

这段代码的逻辑就是：读数据→记初始位置→逐层来：加指示牌数字→算要找第几个楼梯房→找这个房间→更新下一层的位置→最后输出总和。核心是 "模拟"------ 把题目里小明的行动步骤，一步一步翻译成代码，没有复杂算法，只是把规则落地成变量和循环。

相关推荐
世洋Blog15 小时前
AStar算法基础学习总结
算法·面试·c#·astar·寻路
haing201915 小时前
七轴协作机器人运动学正解计算方法
算法·机器学习·机器人
5：0015 小时前
Python进阶语法
开发语言·python
太理摆烂哥15 小时前
C++之异常
java·开发语言·jvm
期待のcode15 小时前
java异常
java·开发语言
崇山峻岭之间15 小时前
Matlab学习记录18
开发语言·学习·matlab
勇往直前plus15 小时前
Python 类与实例对象的内存存储
java·开发语言·python
谈笑也风生15 小时前
把二叉搜索树转换为累加树（一）
算法
youngee1115 小时前
hot100-64跳跃游戏
算法·游戏
热门推荐
01GitHub 镜像站点02手把手教你通过Gemini3 pro 学生认证，白用一年，手慢无！03安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）04jdk21下载、安装（Windows、Linux、macOS）05Linux下V2Ray安装配置指南062025 最新教程：注册并切换到美区 Apple ID07GitLab 零基础入门指南：从安装到项目管理全流程08Claude Code Skills 实用使用手册09Labelme从安装到标注：零基础完整指南10UV安装并设置国内源