有向无环图检测算法和关键路径算法

概念：有向无环图即没有回路的有向图，常用来描述一个系统或工程的行进过程

如何描述工程或子工程活动：

AOV网（Activity On Vertex network）---解决拓扑排序问题---对应系统分析中前驱图解决PV操作的工具
用一个有向图表示一个工程的各自工程及其相互制约关系，其中顶点表示活动，边表示互动间的优先制约关系，称这种有向图为顶点表示活动的网，简称AOV网
- 特点
  - 若从i到j有一条路径，则i是j的前驱，j是i的后继；
  - 若<i, j>是网中的有向边，则i是j的直接前驱，j是i的直接后继；
  - AOV网中不允许有回路，因为如果回路存在，则表明某项活动以自己为先决条件，这是不允许的
- 拓扑排序
  - 定义：在AOV网没有回路的前提下，我们将全部活动排列成一个线性序列，使得若AOV网中有边<i, j>存在，则在这个序列中，i 一定排在 j 的前面，具有这种性质的线性序列称为拓扑有序序列，相应的拓扑有序排序算法称为拓扑排序
    - 如何把AOV网转换成线性有序序列？
      - 找到没有前驱的顶点，然后删掉这个顶点及以全部该顶点为边尾的边；
      - 然后输出这个删掉的顶点为一个拓扑序列活动，按从小到大原则依此删除顶点和边并顺序输出到序列中；
    - 初始AOV网到线性有序序列示意图：（可以自定义原则，比如从小到大，也可以从大到小，拓扑线性有序序列不唯一）
      - 初始AOV网
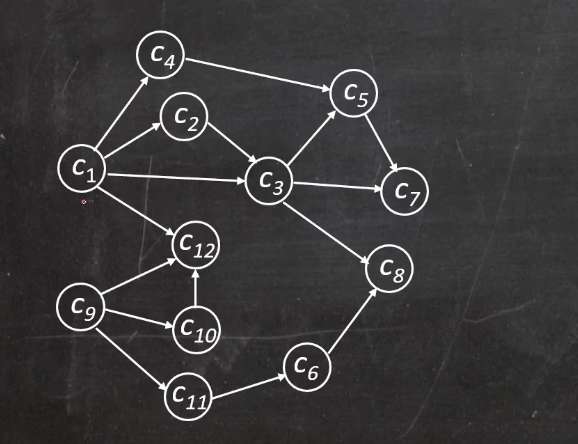
      - 最终输出的线性有序序列结果：
      - 验证：到AOV网中前驱和后继关系
  - 如何检测拓扑图中是否存在回路？
    - 对有向图构造其顶点的拓扑有序序列，若网中所有顶点都在它的拓扑有序序列中，则AOV网中必定不存在环；
AOE网（Activity On Edge nework）---解决关键路径问题---对应高级项目管理中的网络图，用来评估项目排期最长路径最短排期，即关键路径
用一个有向图表示一个工程的各子工程及相互制约关系，其中边表示活动，以顶点表示活动的开始或者结束事件，称这种有向图为边表示活动的网，简称AOV网。
- 使用拓扑排序方式
  - 在各个顶点处标记ve（事件最早开始时间初始值为0）和vl（事件最晚开始时间）
    - 计算ve：
      - v1的ve + 边（活动耗时）得到直接后继顶点（如 v2 的ve = 0 + 2；v3的ve = 0 + 5 ），更新V2和V3的顶点ve的值，记录最大值；
      - 当当前顶点的边都计算完，则删除当前顶点和全部边，继续计算下一个如上方式依此更新顶点ve
      - 示意图
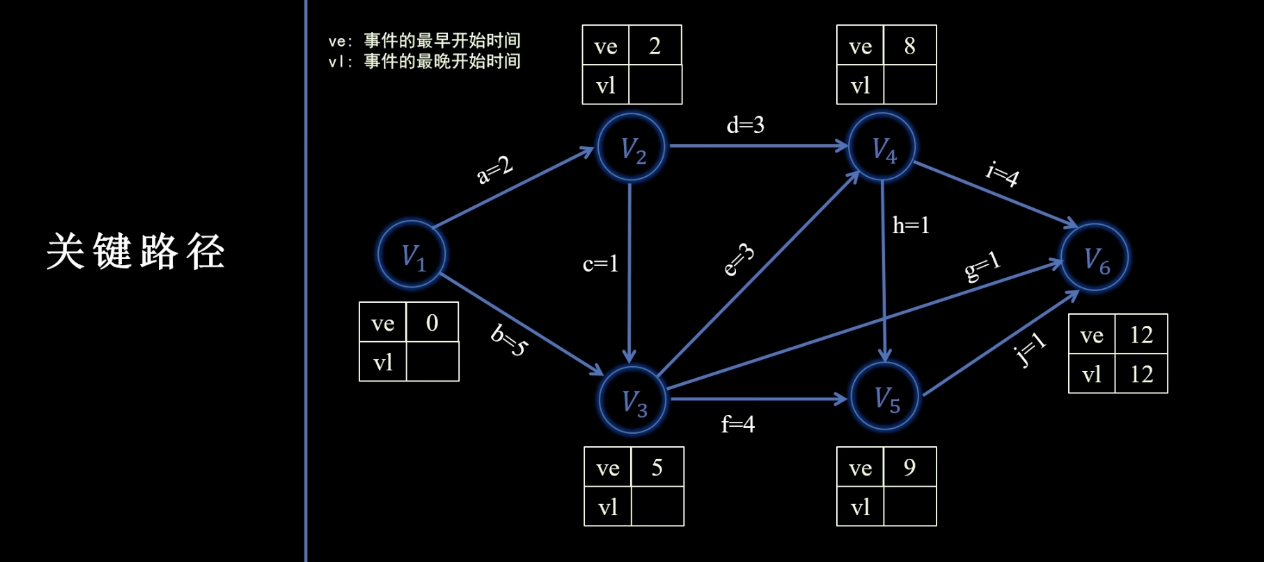
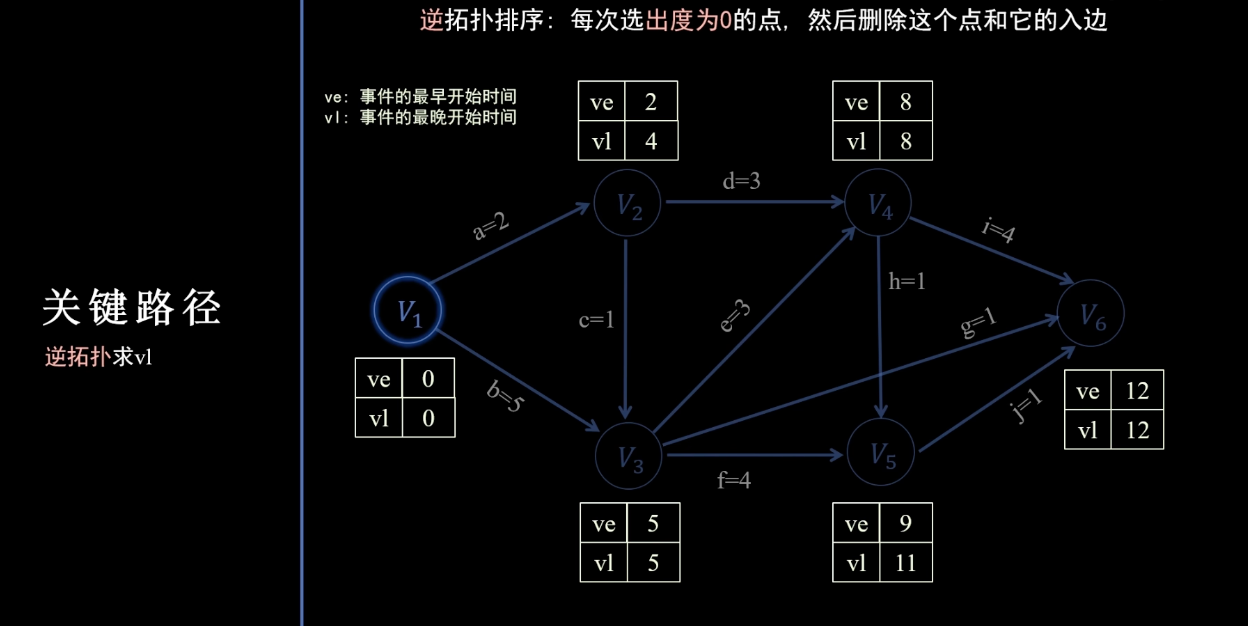
    - 计算vl：逆拓扑排序方法求出最晚开始时间
      - 全部顶点的vl更新为终点V6的ve（如图ve = 12）
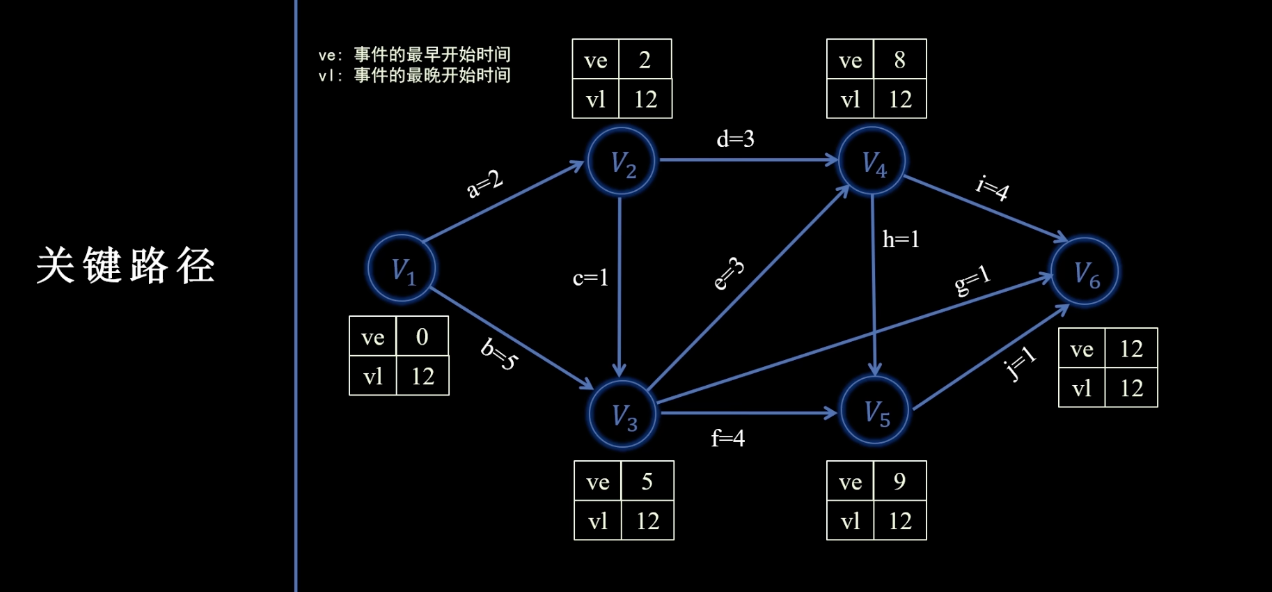
      - 倒序、逆箭头方向，逐个vl减去边的值，多个边时更新成最小值，如下图
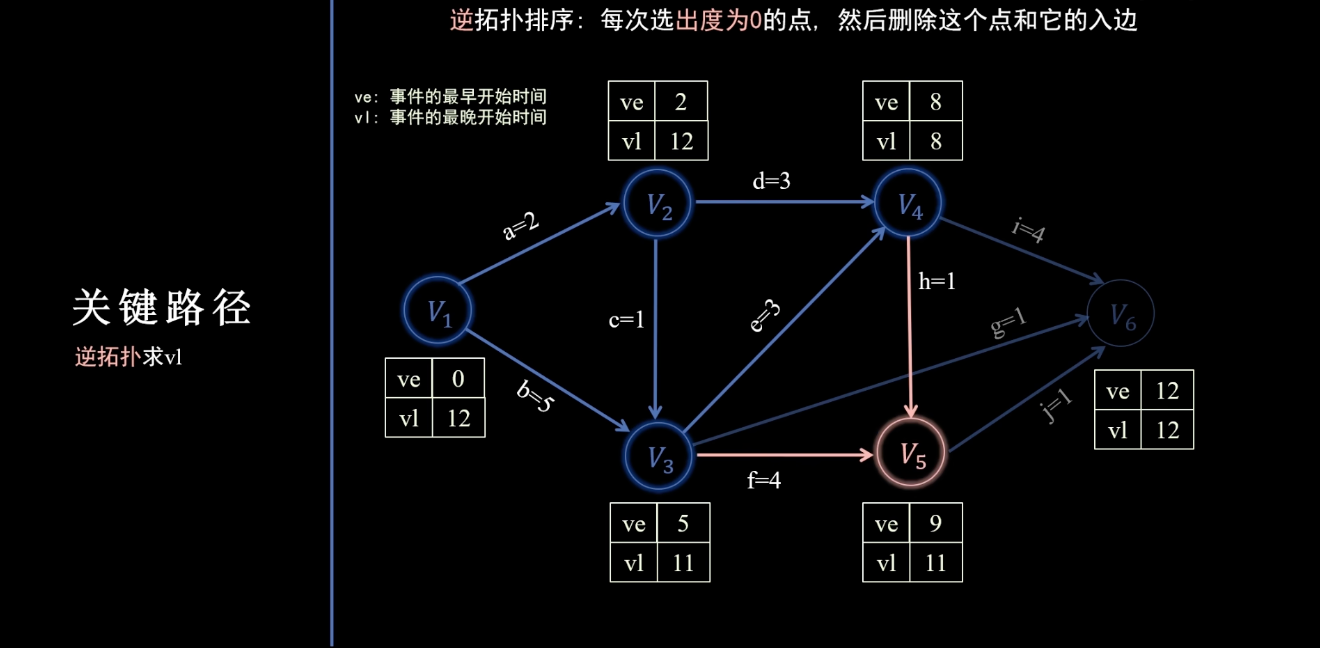
      - 得到各个事件的最早和最晚开始事件结果
      - 总结：先用拓扑排序计算每个顶点的ve（最早开始时间，记录最大值）逆拓扑计算每个顶点vl（最晚开始时间，记录最小值）
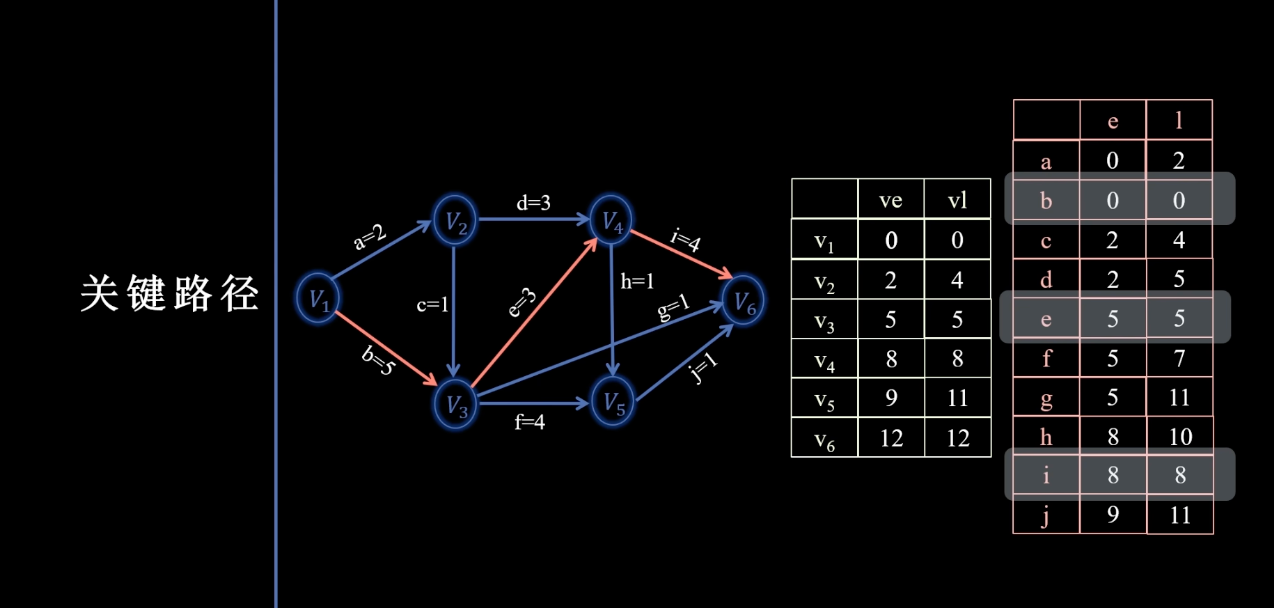
      - 边的最早时间和最晚时间
        
        最早时间e：即顶点的最早开始时间，如c、d活动是V2发出，则c和d活动的最早开始时间都是2，以此类推
        
        最晚时间l: 即被指向顶点的最晚开始时间 - 活动所需时间，如v3的最晚开始时间是5，则c活动的最晚开始时间是5 - 1 = 4以此类推。
      - 汇总成表，各活动的最早和最晚开始时间，找到边（活动）的最早开始时间和最晚开始时间是一样的边，在本图中是b、e、i活动，在途中标出即，关键路径可能不唯一）：