《Multi-Scale Geometric Consistency Guided Multi-View Stereo》
写在前面的话:
这篇文章是对于Gipuma算法的改进。后续还有一些改进工作。
这篇论文提出了一种叫ACMM(多尺度几何一致性引导的多视图立体)的方法,核心是解决传统方法在低纹理区域(比如纯色墙面、光滑地板)深度估计不准的问题。作者发现,低纹理区域在粗尺度上反而更容易识别------就像把模糊的图片缩小后,细节反而清晰了。
ACMH:基础方法的创新突破
ACMH(自适应棋盘格采样和多假设联合视图选择)是ACMM的核心基础。传统方法(如Gipuma)用固定8个方向采样传播假设,而ACMH的创新点在于根据局部区域的结构信息动态选择传播点。比如在一块平面上,它不会机械地选8个固定方向,而是扫描周围更大区域(4个V形+4个长条区域),从匹配代价最低的点中选出8个最优候选假设。这就像在墙面找"最平滑的角落"作为传播起点,而不是随便戳8个点。
更关键的是多假设联合视图选择。ACMH不直接选top-k视图,而是让8个假设共同"投票":对每个像素,计算8个假设下各视图的匹配代价,再用动态阈值τ(t)筛选。如果一个视图在多数假设中匹配代价都低(比如6个假设里有5个代价低于阈值),就把它纳入聚合视图集。同时,对可靠视图赋予更高权重(权重=匹配代价置信度的平均值),避免噪声干扰。这种机制让不同区域能自适应选择最佳视图------在平墙用左右视图,在墙角用上下视图。
为什么ACMH更有效?
传统方法(如[8])用固定k个视图,导致不同假设聚合的视图不同,产生偏差。ACMH的投票机制让所有假设共享同一组聚合视图,保证一致性。实验显示:在Strecha数据集上,ACMH比固定视图选择(DWTA)精度提升2.1%,与COLMAP(当前主流方法)竞争。尤其在低纹理区域(如办公室白墙),ACMH的深度图更平滑,没有COLMAP常见的"鬼影"现象。
ACMM:ACMH的升级版
ACMH解决了基础精度问题,但低纹理区域在细尺度仍有模糊。ACMM的突破在于:
- 多尺度几何一致性:先在粗尺度用ACMH做可靠深度估计(粗尺度下低纹理区域更易分辨),再上采样到细尺度。用几何一致性约束(前后向重投影误差)防止粗尺度的模糊信息污染细尺度,确保可靠估计能传递到细节处。
- 细节恢复器:专门检测边界和薄结构(如门框、踢球机边缘)。当光度一致性代价的差值超过阈值(即当前估计明显错误),就用周围像素的光度信息修正。比如在办公室场景,ACMM能清晰区分地板和墙面的交界,而COLMAP会把交界处糊成一片。
效果与效率的平衡
在ETH3D的办公室、管道等低纹理场景,ACMM比COLMAP精度提升显著(例如办公室场景绝对误差从12.3cm降到8.7cm)。速度上,ACMH比COLMAP快6倍(因棋盘格并行传播),ACMM比ACMH慢约2倍,但仍是COLMAP的3倍快。
文章目录
- 摘要
- 1引言
- 2相关工作
- 3总览
- [4结构化局部信息(Structured Region Information)](#4结构化局部信息(Structured Region Information))
- [5 多尺度几何一致性](#5 多尺度几何一致性)
- 6深度图融合
- 7实验
- 8结论
摘要
我们首先介绍了我们的自适应棋盘格采样和多假设联合视图选择( ACMH )的基本多视图立体方法。
对于低纹理区域的深度估计,我们进一步提出将ACMH与多尺度几何一致性引导( ACMM )相结合,以获得低纹理区域在更粗尺度下的可靠深度估计,并保证其可以传播到更精细的尺度。此外,为了纠正由较粗尺度传播的错误估计,我们提出了一种新的细节恢复器。
1引言
面对大规模数据、低纹理、遮挡、重复模式和反射面等问题,如何在计算机视觉领域实现高效准确的多视点立体视觉仍然是一个具有挑战性的问题。
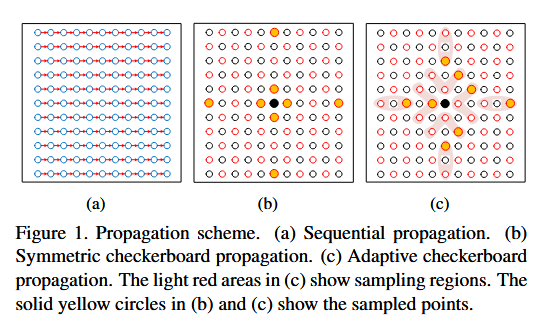
patchmatch包括四个步骤:初始化,传播,视图选择,视差优化。在这个流程中,传播和视图选择是PatchMatch Stereo方法的两个关键步骤。前者对效率很重要,后者对精度很重要。对于传播,一般存在两种截然不同的并行方案:顺序传播[ 1、36、19]和类扩散传播[ 8 ]。前者仅在垂直(或水平)方向上沿平行扫描线遍历像素(图1 ( a ) )。相比之下,后者以棋盘格模式同时更新图像中一半像素的状态(图1 ( b ) )。在效率方面,类扩散传播获得了更好的算法并行性。
在顺序传播中,[ 36、19 ]的结果由于类扩散传播[8],这是因为类扩散传播采用简单的阈值截断方案来确定聚合视图子集,而[ 36、19 ]构造了一个概率图模型来执行逐像素视图选择。
因此,基于棋盘格模式设计出更加稳健的视图选择是一个很好的话题。
提出了一种自适应棋盘格采样方法并联合多个假设约束视图选择(ACMH)。我们的核心思想是基于原始patchmatch的假设,即在一个相对较大的区域内的像素可以用一个3D平面近似建模,与原始patchmatch的固定采样不同,ACMH搜索更大的区域以自适应地采样更好的候选假设进行传播 (图1 ( c ) )。在这些较好的假设下,我们提出了一种多假设联合策略来推断像素级的视图选择。对于特定的像素,该策略采用投票机制为不同的传播假设提供相同的聚合视图子集,并赋予可信视图更大的权重以聚合最终的多视图匹配代价 。因此,ACMH在继承棋盘格图案高效率的同时,能够实现精确的深度图估计。
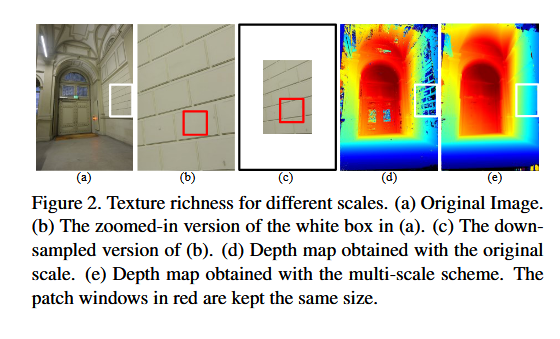
ACMM:低纹理区域的视觉相似性度量一直是一个具有挑战性的问题。如图2 ( b )所示,低纹理区域的低区分度导致视觉相似性的二义性,进一步降低了Patch Match Stereo方法的性能(图2 ( d ) )。然而,我们观察到,对于低纹理区域,虽然图2 ( b )中具有通用patch窗口的纹理信息并不显著,但当对图像进行下采样时,相同补丁窗口下的纹理信息变得更有区分度(图2 ( c ) )。也就是说,纹理丰富度是一个相对的度量。 那么,一个直观的想法是,我们可以在更粗的尺度上估计深度信息,以缓解低纹理区域的歧义性,并将其作为更精细尺度上匹配过程的指导。基于上述思想,本文进一步提出了一种基于几何一致性指导的多尺度块匹配算法( Multiscale patch matching with geometric consistency guidance,ACMM )。具体来说,我们的方法构建了图像金字塔,并在较粗的尺度上获得了低纹理区域的可靠深度估计。通过上采样将这些估计从较粗的尺度传播到较细的尺度后,我们利用几何一致性在细尺度上来约束深度估计。考虑到从较粗尺度到较细尺度的深度传播往往会导致细节信息的丢失,我们提出了一种基于相邻尺度间光度一致性差异图的细节恢复器。通过我们提出的策略,我们的方法不仅可以在低纹理区域估计深度信息,而且可以保留细节。
我们的主要贡献总结如下:1 )继承了类扩散传播的高效性,我们提出了一种自适应棋盘采样方案,根据结构化的区域信息来选择更合理的传播假设。然后,提出一种多假设联合视图选择方法,帮助选择可信的聚合视图。2 )针对低纹理区域的模糊问题,提出了一种几何一致性指导的多尺度块匹配方案。在不同尺度上施加的几何一致性可以保证在较粗尺度上获得的低纹理区域的可靠深度估计在较细尺度上得到保留。此外,为了校正由较粗尺度传播的误差,提出了一种细节恢复器。 通过广泛的评估,我们在Strecha数据集[ 27 ]和ETH3D基准数据集[ 21 ]上取得了最先进的性能,证明了我们方法的有效性和效率。
2相关工作
根据文献[ 22 ],MVS方法可以分为4类:基于体素的方法[ 5,29,26]、基于表面演化的方法[ 4、11、3]、基于面片的方法[ 9、17、7]和基于深度图的方法[ 36、8、19]。基于体素的方法往往受到其预定义的体素网格分辨率的约束。基于表面演化的方法依赖于一个好的初始解。对于基于面片的方法,其对匹配关键点的依赖会损害三维模型的完整性。基于深度图的方法需要估计所有图像的深度图,然后将它们融合到统一的三维场景表示中。[ 22、6 ]对MVS方法进行了较为详细的综述。我们的方法属于最后一类,我们只讨论相关的PatchMatch Stereo方法。
在效率方面,[ 1、30、36、19]采用顺序传播方案。它们在奇数迭代步交替进行向上/向下传播,在偶数迭代步交替进行向左/向右传播。为了增加并行性,文献[ 30 ]选取图像高度(宽度)的八分之一作为垂直(水平)传播中每条扫描线的长度。然而,顺序传播的算法并行度仍然与图像的行数或列数成正比。然后,加利亚尼等人[ 8 ]提出利用棋盘格模式来执行类扩散传播方案。它允许同时更新图像中一半像素的状态。但是,他们忽略了好的假设在传播中应该具有优先性。
根据上述传播策略,许多视图选择方案被提出来应对传播过程中的噪声。在类扩散传播方案中,[ 8 ]以最小的k匹配代价选择固定的k个视图。然而,这会导致由于不同的聚集子集对于不同的假设产生偏差。在顺序传播中,[1 , 30]也只要求全局视角,而忽略了逐像素的视角选择。为了在每个像素处仅包含有用的相邻视图,Zheng等人[ 36 ]首先尝试构建一个概率图模型来联合估计深度图和视图选择。进一步,Scho ̈ nberger等人[ 19 ]引入了几何先验和时间光滑性来更好地刻画状态转移概率。
虽然一些方法侧重于视图选择,以提高局部平滑性,并获得了一些好处,但它们仍然受到补丁窗口大小的限制。为了在低纹理区域感知更多有用的信息,Wei等人[ 30 ]采用了基于方差一致性的多尺度块匹配。然而,这种一致性太强,以至于在多个视图之间的少数相邻视图中传播一些可靠的估计。此外,他们忽略了细节上的错误。
3总览
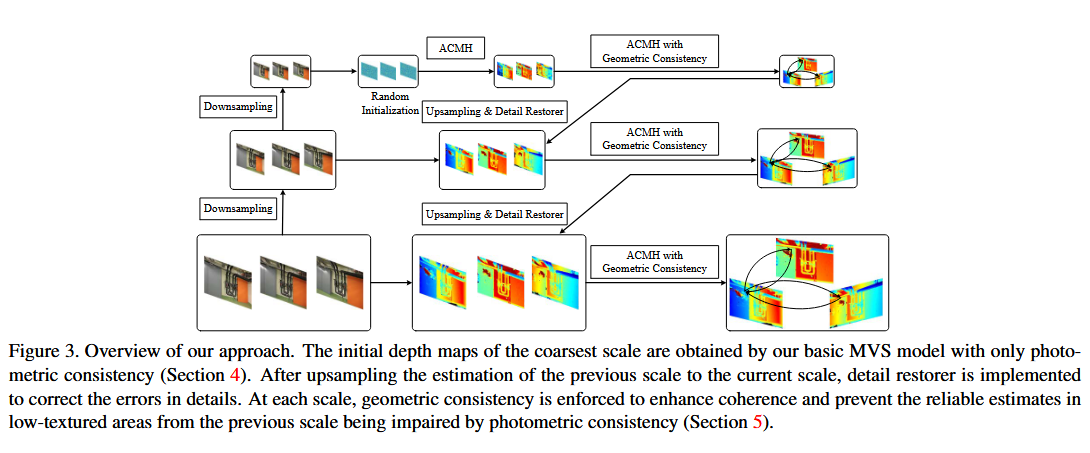
给定一组具有已知标定摄像机参数P = { Pi | i = 1 · · · N }的输入图像I = { Ii | i = 1 · · · N },我们的目标是估计所有图像的深度图D = { Di | i = 1 · · · N },并将它们融合成三维点云。具体来说,我们的目标是在源图像Isrc的指导下,从I中依次选择参考图像Iref来恢复深度图。
我们的目的是从更粗的尺度传播低纹理区域的可靠估计,以帮助在细节上没有太大损失的更精细尺度的估计。具体做法如下:
我们首先使用我们的具有光度一致性的基本MVS模型ACMH,在最粗糙的尺度上获得所有图像的初始深度图。为了增强所有深度图之间的一致性,我们进一步执行具有几何一致性的ACMH。
然后我们将深度图上采样到下一个尺度。上采样将低纹理区域中可靠的深度估计传播到当前尺度,这些深度估计是在上一个尺度下获得的。
最后,为了纠正由前一尺度引起的误差,首先使用了一个细节恢复器。这些校正后的深度图被用作初始化,以指导后续具有几何一致性的ACMH,从而在当前尺度下保持和优化低纹理区域内的可靠估计。
重复相同的上采样、细节恢复和具有几何一致性的ACMH,直到获得原始图像尺度下的深度图。我们称之为我们的整体方法ACMM。
对某一次金字塔图像进行多视图立体匹配的过程称为ACMH,ACMH可以看成ACMM的一个子集。ACMM相对于ACMH多了一个金字塔过程和一个几何约束,不涉及到多层金字塔迭代的过程。
4结构化局部信息(Structured Region Information)
结构化区域信息是指相对较大区域内的像素可以近似地被同一个3D平面建模。我们的自适应棋盘格采样和多假设联合视图选择( ACMH )的基本MVS方法受此启发,以采样更好的候选假设进行传播,并选择可信度更高的视图进行多视图匹配代价聚合。ACMH的具体内容如下所示:
4.1随机初始化
这一步和文献8一样
4.2自适应棋盘格采样
我们首先采用[ 8 ]中的思想将Iref的像素划分为棋盘格的红黑网格。这种模式允许我们同时使用红色像素更新黑色像素的假设,反之亦然。在[ 8 ]中,他们的方法从八个固定的位置采样。不同的是,对于红色或黑色组中的每个像素,我们将这8个点扩展为4个V形区域和4个长条形区域(图1 ( c ) )。每个V形区域包含7个 样本,每个长条形区域包含11个 样本(原文的图和这里的表述不太符合,原图是3个样本+3个样本)。然后根据这些区域先前的多视角匹配成本 ,从这些地区中挑选出8个好的假设。这种采样方案受到结构化区域信息的青睐。也就是说,多视图匹配代价更小的假设将更好地代表局部平面。 这种策略有助于局部共享区域的一个好的平面尽可能地进一步扩散,并提供更紧凑的估计。
4.3多假设联合的视图选择
这里也可以说是多个假设条件约束的视图选择,这也是ACMH的核心,也是相对于文献8的核心改进之处。
为了获得每个像素 的鲁棒的多视图匹配代价,我们进一步利用这8个假设来推断每个相邻视图的权重。对于像素p,我们利用传播假设计算其对应的匹配代价,并将其嵌入到代价矩阵中。
M = [ m 1 , 1 m 1 , 2 ⋯ m 1 , N − 1 m 2 , 1 m 2 , 2 ⋯ m 2 , N − 1 ⋮ ⋮ ⋱ ⋮ m 8 , 1 m 8 , 2 ⋯ m 8 , N − 1 ] \mathbf{M}=\left[\begin{array}{cccc} m_{1,1} & m_{1,2} & \cdots & m_{1, N-1} \\ m_{2,1} & m_{2,2} & \cdots & m_{2, N-1} \\ \vdots & \vdots & \ddots & \vdots \\ m_{8,1} & m_{8,2} & \cdots & m_{8, N-1} \end{array}\right] M= m1,1m2,1⋮m8,1m1,2m2,2⋮m8,2⋯⋯⋱⋯m1,N−1m2,N−1⋮m8,N−1
其中,mij为第j个视角Ij对第i个假设hi的匹配代价(简单的来说就是源图像(src)的像素点与参考图像(ref)像素点的代价)。我们采用归一化互相关的双边加权自适应[ 19 ]来计算匹配代价,它描述了参考块和源块之间的光度一致性。
为了从上述成本矩阵推断聚合视图,我们在每个列中应用投票决策来确定视图是否合适。这背后的一个关键观察是,对于一个糟糕的视图,其对应的八项匹配成本总是很高。相比之下,一个好的视图总是有一些较小的匹配代价。此外,好视图的匹配代价会随着算法的迭代而降低。因此,一个好的匹配成本边界定义为:
τ ( t ) = τ 0 ⋅ e − t 2 α , \tau(t)=\tau_0 \cdot e^{-\frac{t^2}{\alpha}}, τ(t)=τ0⋅e−αt2,
where t t t means the t t t-th iteration, τ 0 \tau_0 τ0 is the initial matching cost threshold and α \alpha α is a constant. Besides, we define a fixed bad matching cost threshold τ 1 ( τ 1 > τ ( t ) ) \tau_1\left(\tau_1>\tau(t)\right) τ1(τ1>τ(t)).
对于一个视图 I j I_j Ij,像素数量上存在多于 n 1 n_1 n1 满足: m i , j < τ ( t ) m_{i, j}<\tau(t) mi,j<τ(t),我们定义一个集合 S good ( j ) \mathrm{S}{\text {good }}(j) Sgood (j) 来计算 I j I_j Ij 权重(这里存放的是满足该条件的像素数量)。 同时也有像素数量少于 n 2 n_2 n2 数量,满足: m i , j > τ 1 m{i, j}>\tau_1 mi,j>τ1. 。同时满足这两个条件会将这个视图放入视图选择集合 S t \mathrm{S}_t St 。
由于噪声、视点和尺度等因素的影响,上述推断的视角选择集St可能包含一些不稳定的视角。这意味着每个选择的视图将对最终的聚合匹配成本贡献不同的权重。为了评估每个选择视图的重要性,匹配代价的置信度计算如下:
C ( m i j ) = e − m i j 2 2 β 2 . C\left(m_{i j}\right)=e^{-\frac{m_{i j}^2}{2 \beta^2}} . C(mij)=e−2β2mij2.
where β \beta β is a constant. This makes good views more discriminative. The weight of each selected view can be defined as
w ( I j ) = 1 ∣ S good ( j ) ∣ ∑ m i , j ∈ S good ( j ) C ( m i , j ) , I j ∈ S t . w\left(I_j\right)=\frac{1}{\left|\mathrm{~S}{\operatorname{good}}(j)\right|} \sum{m_{i, j} \in \mathrm{~S}{\text {good }}(j)} C\left(m{i, j}\right), I_j \in \mathrm{~S}_t . w(Ij)=∣ Sgood(j)∣1mi,j∈ Sgood (j)∑C(mi,j),Ij∈ St.
为了将第t-1次迭代的视图传递到第t次,因此对权重进行修改:
w ′ ( I j ) = { ( I ( I j = v t − 1 ) + 1 ) ⋅ w ( I j ) , if I j ∈ S t ; 0.2 ⋅ I ( I j = v t − 1 ) , else. w^{\prime}\left(I_j\right)= \begin{cases}\left(\mathbb{I}\left(I_j=v_{t-1}\right)+1\right) \cdot w\left(I_j\right), & \text { if } I_j \in \mathrm{~S}t ; \\ 0.2 \cdot \mathbb{I}\left(I_j=v{t-1}\right), & \text { else. }\end{cases} w′(Ij)={(I(Ij=vt−1)+1)⋅w(Ij),0.2⋅I(Ij=vt−1), if Ij∈ St; else.
where I ( ⋅ ) \mathbb{I}(\cdot) I(⋅) is an indicator function such that I ( \mathbb{I}( I( true ) = 1 )=1 )=1 and I \mathbb{I} I (false) = 0 =0 =0. 也就是说如果在上一次视图选择集合中,那么权重就乘以2否则乘以0.2. 因此重新定义加权后的匹配代价:
m photo ( p , h i ) = ∑ j = 1 N − 1 w ′ ( I j ) ⋅ m i , j ∑ j = 1 N − 1 w ′ ( I j ) (6) m_{\text {photo }}\left(p, h_i\right)=\frac{\sum_{j=1}^{N-1} w^{\prime}\left(I_j\right) \cdot m_{i, j}}{\sum_{j=1}^{N-1} w^{\prime}\left(I_j\right)} \tag{6} mphoto (p,hi)=∑j=1N−1w′(Ij)∑j=1N−1w′(Ij)⋅mi,j(6)
当前像素p的最佳估计由具有最小多视图聚合成本的假设来更新。这里会根据计算的代价值,选最小的8个作为棋盘格采样点,然后进行传播(回到了4.2).
4.4细化
在每次红黑迭代后,应用一个细化步骤来丰富解空间的多样性。对于当前像素p的深度和法向,存在三个条件,即其中之一,两者都不存在,或者两者都接近最优解[ 19 ]。这样,我们就产生了两个新的假设,其中一个是随机产生的,另一个是通过对当前估计值进行扰动得到的。我们将这些新的深度和正常值与当前的深度和正常值结合起来,产生了另外六个新的待检验的假设。选择总成本最小的假设作为像素p的最终估计值。对Iref进行上述传播、视图选择和精化,重复多次得到最终的深度图。 最后,一个5 × 5大小的中值滤波器被应用到我们最终的深度图中。
ACMH到这里就结束了。
5 多尺度几何一致性
结合多尺度方案,最粗尺度的ACMH在低纹理区域获得更可靠的深度估计。然而,光度一致性在应用于在更精细尺度上优化这些深度估计时遇到了困难。在这一部分,我们详细介绍了如何利用几何一致性 指导来处理这些估计的优化问题。此外,还提出了一个细节恢复器来校正由较粗尺度引起的误差。这是ACMM的核心。
5.1几何一致性引导
在最粗尺度上获得低纹理区域的可靠深度估计并通过上采样传播到更精细的尺度后,我们需要在更精细的尺度上优化这些估计。我们的核心思想是,源图像的上采样深度图可以在几何上限制这些估计不受光度一致性的干扰,即几何一致性。受[ 34、19 ]的启发,我们使用前后向重投影误差来表示这种一致性。
记图像 I i I_{i} Ii上像素点p的深度为 D i ( p ) D_{i}(p) Di(p) , 相机参数 P i = [ M i ∣ p i , 4 ] P_{i} = \left[M_{i} \mid \mathrm{p}{i, 4}\right] Pi=[Mi∣pi,4] , 对应的三维坐标 X i ( p ) X{i}(p) Xi(p) :
X i ( p ) = M i − 1 ⋅ ( D i ( p ) ⋅ p − p i , 4 ) . X_{i}(p) = M_{i}^{-1} \cdot\left(D_{i}(p) \cdot p-\mathrm{p}_{i, 4}\right) . Xi(p)=Mi−1⋅(Di(p)⋅p−pi,4).
参考图像 I ref I_{\text {ref }} Iref 和源图像 I j I_{j} Ij 的重投影误差:
Δ e i , j = min ( ∣ P r e f ⋅ X j ( P j ⋅ X r e f ( p ) ) − p ∣ , δ ) , \Delta e_{i, j} = \min \left(\left|P_{\mathrm{ref}} \cdot X_{j}\left(P_{j} \cdot X_{\mathrm{ref}}(p)\right)-p\right|, \delta\right), Δei,j=min(∣Pref⋅Xj(Pj⋅Xref(p))−p∣,δ),
从而得到加入几何一致性约束的代价:
m g e o ( p , h i ) = ∑ j = 1 N − 1 w ′ ( I j ) ⋅ ( m i , j + λ ⋅ Δ e i , j ) ∑ j = 1 N − 1 w ′ ( I j ) (9) m_{\mathrm{geo}}\left(p, h_{i}\right) = \frac{\sum_{j = 1}^{N-1} w^{\prime}\left(I_{j}\right) \cdot\left(m_{i, j}+\lambda \cdot \Delta e_{i, j}\right)}{\sum_{j = 1}^{N-1} w^{\prime}\left(I_{j}\right)}\tag{9} mgeo(p,hi)=∑j=1N−1w′(Ij)∑j=1N−1w′(Ij)⋅(mi,j+λ⋅Δei,j)(9)
where λ \lambda λ is a factor that balances the weight of the two terms.
具体来说,在第l个尺度( l > 0),我们使用联合双边上样器[ 15 ]将上一尺度的估计传播到当前尺度。上采样后的估计值作为当前尺度的初始种子,以执行ACMH中的后续传播、视图选择和精化。不同的是,这里我们采用公式9而不是公式6来更新像素p的假设。实际上,这种修改限制了当前假设更新的解空间,特别是对于低纹理区域的假设更新。这保证了在最粗尺度下得到的低纹理区域的可靠估计可以传播到最细尺度。 值得注意的是,几何一致性还优化了除低纹理区域外的其他区域的深度估计。我们也在最粗的尺度上进行几何一致性来优化这些初始深度图。直觉上,如果更准确地估计出相邻的深度图,则参考图像的深度图会得到进一步的提升。因此,在我们的实验中,我们进行了两次几何一致性引导来细化每个尺度下的深度图。
5.2细节恢复器
多尺度几何一致性指导一方面有助于低纹理区域的估计,但另一方面往往会导致细节模糊。在较粗的尺度上,丢失的图像细节直接导致其深度信息的丢失。此外,固定的窗口尺寸使得ACMH难以实现薄结构和低纹理区域之间的折衷,因为局部平面假设对细节不成立 。此外,虽然上采样可以将低纹理区域的可靠估计扩散到更大的区域,但在细节上也会带来一些额外的误差。

如图4 ( a )所示,模糊的细节往往出现在较薄的结构或边界上。我们希望能探测到这些区域,并只在这些特定区域实施光度一致性,以纠正错误的估计。具体来说,在我们对上一个尺度的估计(即深度和正常)进行上采样后,我们使用它们重新计算当前尺度下的光度一致性代价Cl init。 然后,执行基本的MVS模型,得到新的光度一致性代价Cl photo。如果光度一致性代价的差值满足,像素p的估计将被认为是一个错误:
C init l ( p ) − C photo l ( p ) > ξ , C_{\text {init }}^l(p)-C_{\text {photo }}^l(p)>\xi, Cinit l(p)−Cphoto l(p)>ξ,
其中,ξ是一个很小的常数值,增加了区分错误估计的稳健性。同时,错误的估计将被反映上述差异的假设所取代。通过结合细节恢复器,ACMM可以在低纹理区域和细节之间做出更好的权衡,如图4 ( f )所示。也就是说根据金字塔图像灰度信息差异判断是否是边界或者薄的结构,灰度信息差异大于阈值,然后我没理解这里怎么做。
6深度图融合
具体来说,我们依次将每幅图像作为参考图像,将其深度图转换为世界坐标中的3D点,并将其投影到其相邻视图中,以获得相应的匹配。我们定义了一个满足相对深度差≤0的一致匹配。01,法线夹角θ≤30 °,重投影误差ψ≤2,如文献[ 19 ]。如果存在n≥2个相邻视图,其对应的匹配满足上述约束,则深度估计将被接受。最后,将这些一致深度估计对应的3D点和法向估计平均为一个统一的3D点。
7实验
7.2深度评价
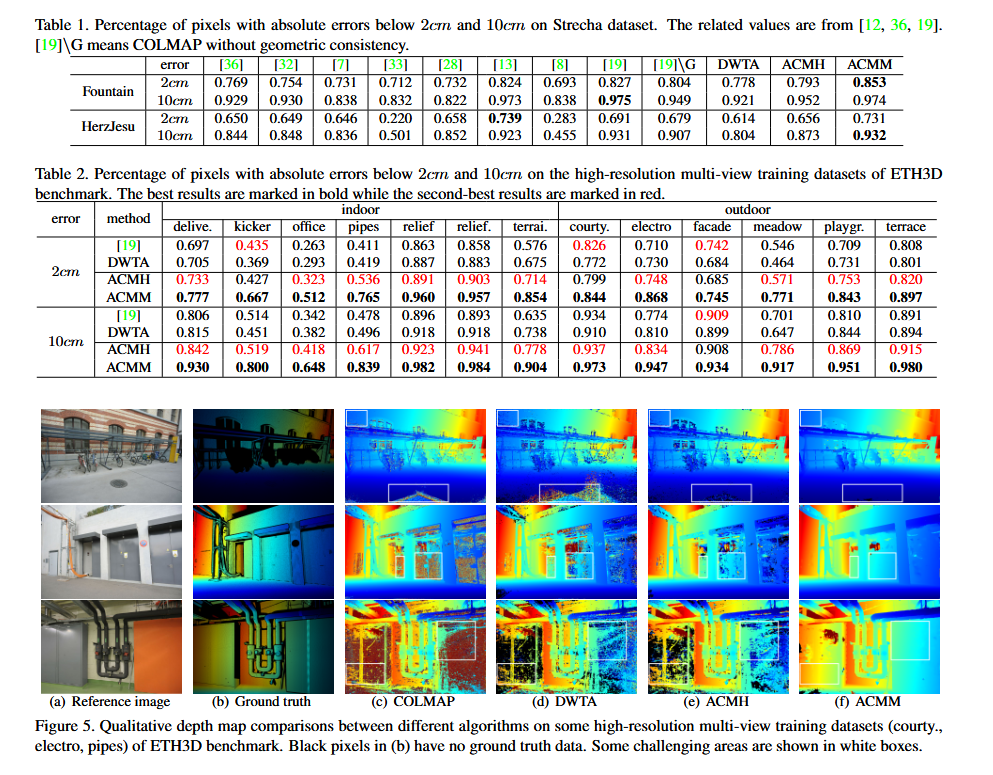
本节将在Strecha数据集和ETH3D基准数据集上评估本文方法在深度图估计上的有效性。根据[ 12 ],我们在表1中计算了绝对深度误差小于2cm和10cm的像素的百分比。为了说明结构化区域信息的有效性,我们将ACMH中的自适应棋盘采样和多假设联合视图选择替换为类扩散传播和top - k - winners - take - all视图选择,记为DWTA 。可以看出,在具有结构化区域信息的情况下,ACMH的性能优于DWTA,与COLMAP [ 19 ]也具有竞争力。更进一步,我们看到ACMM以一个值得注意的幅度超过了ACMH,并且在该数据集中几乎达到了最好的性能。
为了反映真实世界场景中更多的挑战,例如低纹理区域和薄结构,我们进一步将我们的重建深度图与COLMAP进行了比较。表2中ETH3D基准的分辨率多视图训练数据集。我们看到ACMM在这些具有挑战性的数据集上明显优于COLMAP,特别是在一些室内数据集,包括纹理较差的区域,如踢球器、办公室和管道。此外,ACMH几乎达到了次优性能。图5举例说明了COLMAP,DWTA,ACMH和ACMM估计的深度图。可以看出,ACMH也比DWTA表现得更好,并且由于它利用了结构化的区域信息,在低纹理区域中产生了比COLMAP和DWTA更鲁棒的结果。值得注意的是,虽然COLMAP在一些纹理良好的数据集(如法院和门面)中的表现优于DWTA和ACMH,但在一些具有挑战性的数据集(如电子和办公室)中的表现比DWTA和ACMH差。
7.3 点云评价
在这一部分,进行融合,以获得更一致的点云。我们在ETH3D基准的高分辨率多视图测试数据集上评估了我们的点云。表3列出了PMVS [ 7 ],Gipuma [ 8 ],LTVRE [ 16 ],COLMAP,ACMH和ACMM估计的点云的准确性,完整性和F1分数。所有这些方法在准确性方面都显示出类似的结果。在F1分数方面,ACMH因其良好的深度图估计而与其他方法具有竞争力。此外,ACMM继承了ACMH的结构化区域特性,并与多尺度方案相结合,因此优于其他方法。此外,ACMM在包含更多低纹理区域的室内数据集上获得了比其他方法更高的完整性。 这是因为ACMM在这些领域感知到了更可信的信息。
7.4运行时间
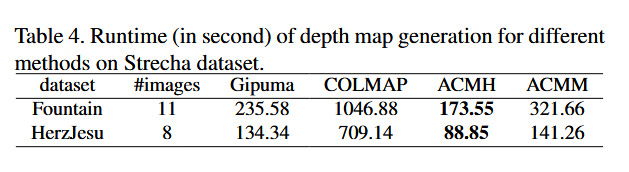
我们将属于Patch Match Stereo范围的不同方法生成深度图的运行时间列于表4。所有这些方法都是通过我们相同的平台在单个GPU上进行的3。ACMH和Gipuma均在6次迭代后收敛,而COLMAP采用10次迭代。对于ACMM,最粗尺度需要7次迭代,其他尺度需要6次迭代。如表4所示,ACMH比COLMAP快6倍左右。这是因为COLMAP的顺序传播只更新一次一行(列)像素及其每次迭代的状态在4个方向上。
虽然ACMH和Gipuma都利用了棋盘格传播,但ACMH也比Gipuma更快。这主要是由于Gipuma使用了二分细化,从而产生了更多不必要的假设来测试。对于ACMM,多尺度几何一致性算法需要花费额外的计算时间。然而,由于ACMM在较粗尺度上的几何一致性是在降采样图像上进行的,因此ACMM的运行时间不超过ACMH的两倍。因此,它仍比COLMAP快3倍左右。
8结论
在这项工作中,我们提出了一种新颖的多视图立体方法,用于有效和高效的深度图估计。基于结构化的区域信息,我们首先提出了基于自适应棋盘采样和多假设联合视图选择( ACMH )的基本MVS方法。这些策略有助于尽快传播好的假设,并推断像素级的视图选择。针对低纹理区域的深度估计,我们进一步将ACMH与我们提出的多尺度几何一致性引导方案( ACMM )相结合。多尺度几何一致性和细节恢复器有助于在保留细微细节的同时,获得对低纹理区域更多的区分。 在实验中,我们证明了我们的方法可以获得平滑和一致的深度图估计以及完整的稠密3D模型,同时保持了良好的效率,这表明我们的方法具有很好的应用前景。