运动规划实战案例 | 基于采样的MPC控制(MPPI)算法(附ROS C++/Python仿真)

1 MPPI算法动机

在机器人控制、自动驾驶和无人机导航等领域，系统往往需要在不确定和动态变化的环境中实现高精度、鲁棒性的轨迹跟踪。传统控制方法如PID控制或基于模型的预测控制（MPC），虽然在许多场景中表现良好，但它们通常依赖于精确的系统模型和梯度信息。当系统模型复杂或存在显著不确定性时，这些方法的性能可能不稳定。此外，传统优化方法在实时性要求高的场景中可能面临计算瓶颈，特别是面对非凸问题难以在有限时间内找到全局最优解。

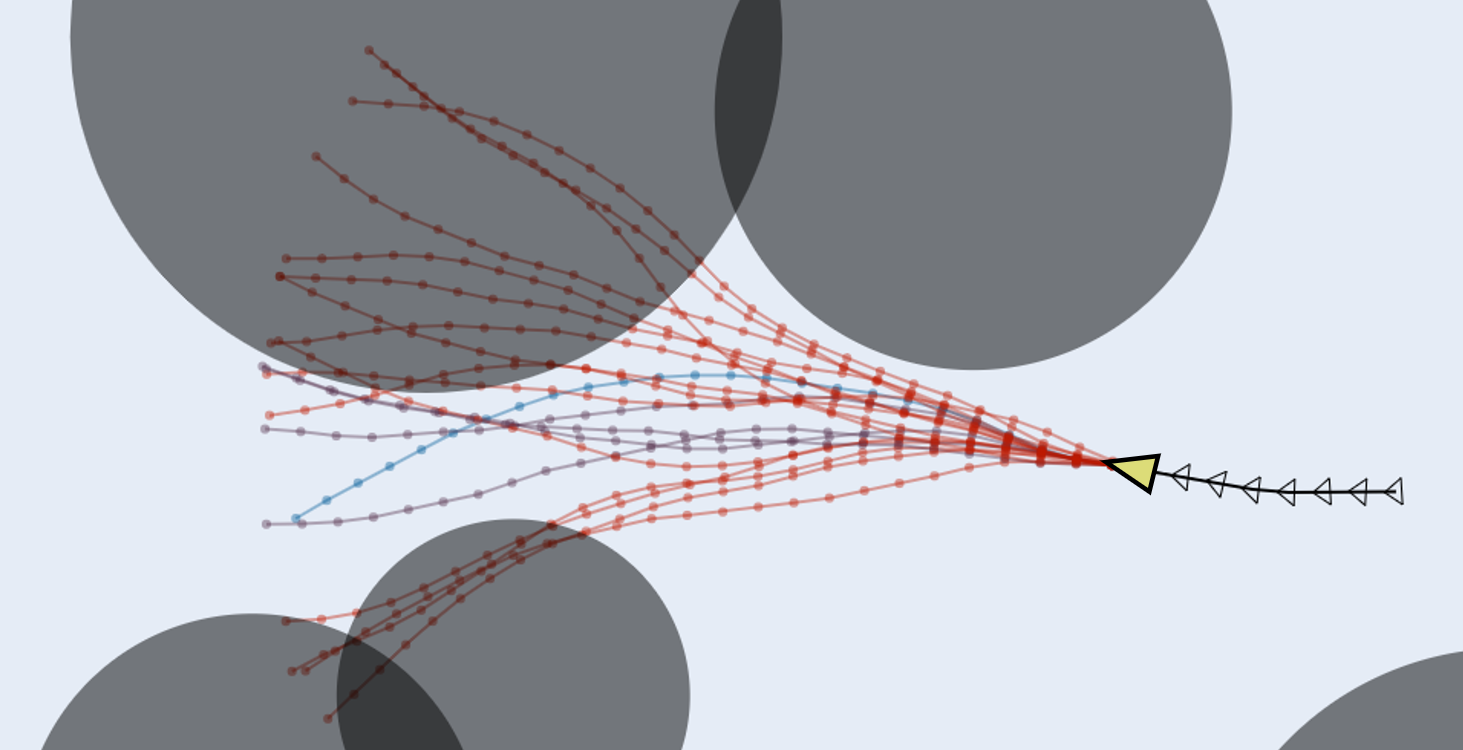
**模型预测路径积分控制（Model Predictive Path Integral, MPPI）**正是在这样的背景下应运而生的一种控制策略。它属于随机采样模型预测控制方法，通过大量采样来近似系统的随机动态，从而在不需要梯度信息的情况下处理非线性、非高斯噪声系统。MPPI的核心优势在于其能够通过并行采样和计算高效地处理高维状态空间，并在实时控制中实现鲁棒性。因此，MPPI为现代无人系统的智能控制提供了一种新的解决思路，弥补了传统方法依赖于梯度信息导致的灵活性不足。

2 MPPI算法原理

MPPI的数学基础建立在随机最优控制理论框架之上。考虑一个离散时间的动态系统，其状态转移由非线性函数 F \mathbf{F} F 描述，即

x t + 1 = F ( x t , v t ) \mathbf{x}_{t+1} = \mathbf{F}(\mathbf{x}_t, \mathbf{v}_t) xt+1=F(xt,vt)

其中 x t ∈ R n \mathbf{x}_t \in \mathbb{R}^n xt∈Rn 是系统状态， v t ∈ R m \mathbf{v}_t \in \mathbb{R}^m vt∈Rm 是控制输入。控制目标是最小化从初始状态 x 0 \mathbf{x}_0 x0 出发的期望累积成本，包括终端成本 ϕ ( x T ) \phi(\mathbf{x}_T) ϕ(xT) 和运行成本 c ( x t ) c(\mathbf{x}_t) c(xt)。

MPPI通过采样随机输入序列来近似期望成本。首先，定义均值控制序列

U = ( u 0 , u 1 , . . . , u T − 1 ) U = (\mathbf{u}_0, \mathbf{u}1, ..., \mathbf{u}{T-1}) U=(u0,u1,...,uT−1)

通常使用上一时刻的最优序列作为初始值。然后，围绕 U U U 进行随机采样，生成 K K K 个输入序列

V k = ( v 0 k , v 1 k , . . . , v T − 1 k ) V_k = (\mathbf{v}_0^k, \mathbf{v}1^k, ..., \mathbf{v}{T-1}^k) Vk=(v0k,v1k,...,vT−1k)

其中 v t k = u t + ϵ t k \mathbf{v}_t^k = \mathbf{u}_t + \epsilon_t^k vtk=ut+ϵtk， ϵ t k ∼ N ( 0 , Σ ) \epsilon_t^k \sim \mathcal{N}(0, \Sigma) ϵtk∼N(0,Σ) 是服从零均值高斯分布的噪声。这些采样序列通过系统模型进行前向模拟，得到对应的状态轨迹

H ( V k ; x 0 ) = ( x 0 , x 1 k , . . . , x T k ) \mathcal{H}(V_k; \mathbf{x}_0) = (\mathbf{x}_0, \mathbf{x}_1^k, ..., \mathbf{x}_T^k) H(Vk;x0)=(x0,x1k,...,xTk)

并计算每条轨迹的成本

S ( V k ; x 0 ) = ϕ ( x T k ) + ∑ t = 0 T − 1 c ( x t k ) S(V_k; \mathbf{x}_0) = \phi(\mathbf{x}T^k) + \sum{t=0}^{T-1} c(\mathbf{x}_t^k) S(Vk;x0)=ϕ(xTk)+t=0∑T−1c(xtk)

接下来，利用采样MPC理论将期望最优控制输入表示为加权平均。为每个采样序列分配权重

w ( V k ) = exp ⁡ ( − 1 λ S ( V k ; x 0 ) ) ∑ j = 1 K exp ⁡ ( − 1 λ S ( V j ; x 0 ) ) w(V_k) = \frac{\exp(-\frac{1}{\lambda} S(V_k; \mathbf{x}0))}{\sum_{j=1}^K \exp(-\frac{1}{\lambda} S(V_j; \mathbf{x}_0))} w(Vk)=∑j=1Kexp(−λ1S(Vj;x0))exp(−λ1S(Vk;x0))

其中 λ > 0 \lambda > 0 λ>0 是温度参数，用于调节权重对成本差异的敏感度。这种指数加权机制确保了低成本轨迹获得更高权重，从而引导控制策略向更优方向更新。最终，更新后的最优控制序列由

u t i + 1 = u t i + ∑ k = 1 K w ( V k ) ϵ t k \mathbf{u}_t^{i+1} = \mathbf{u}t^i + \sum{k=1}^K w(V_k) \epsilon_t^k uti+1=uti+k=1∑Kw(Vk)ϵtk

给出，即当前均值加上加权噪声扰动。这一更新规则无需梯度计算，而是通过采样直接估计控制输入的分布偏移，从而实现了在随机环境中的高效优化。

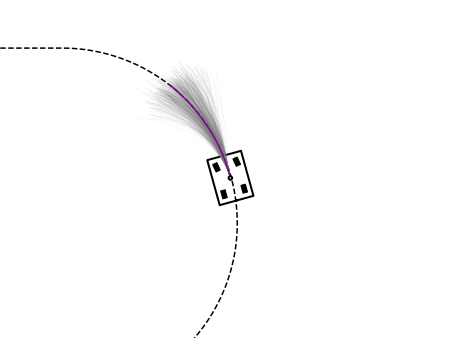
3 算法仿真

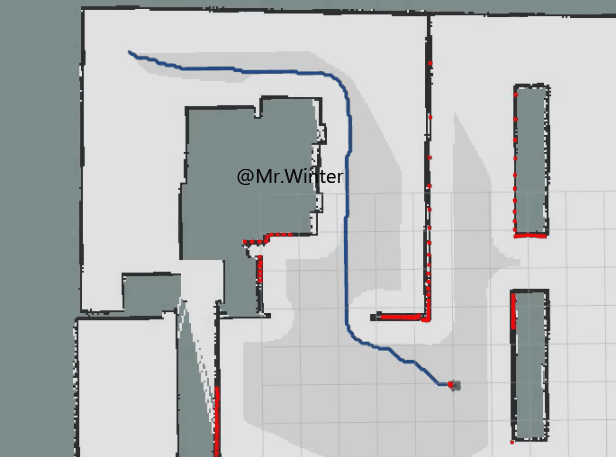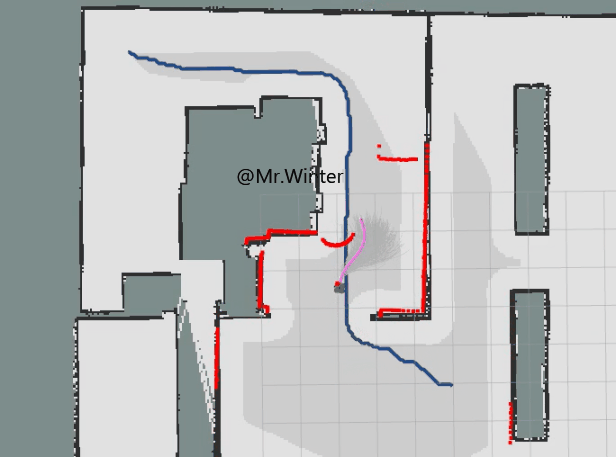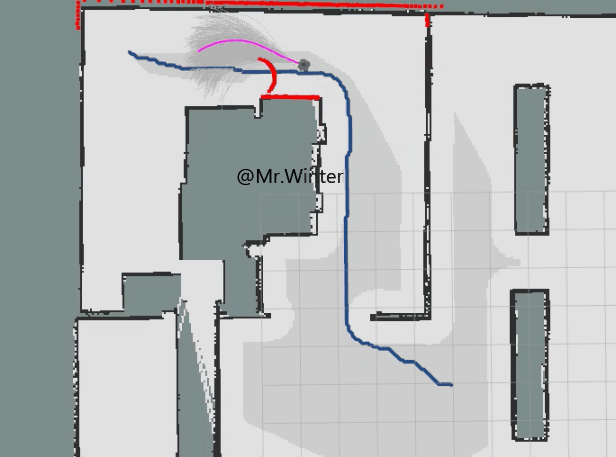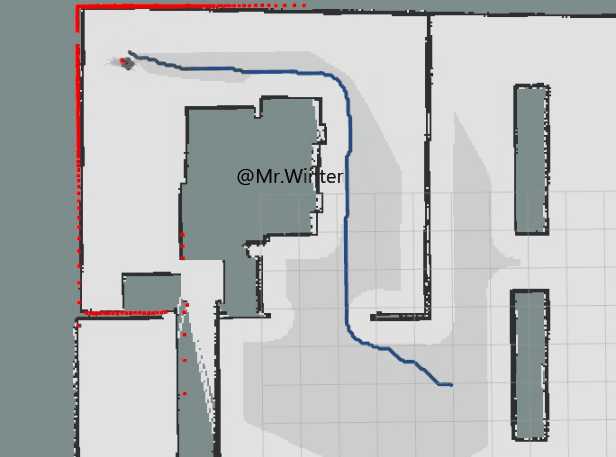
3.1 ROS C++仿真

以下是MPPI控制的核心代码

cpp 复制代码

bool MPPIController::computeVelocityCommands(geometry_msgs::Twist& cmd_vel) {
  if (!initialized_) {
    R_ERROR << "MPPI Controller has not been initialized";
    return false;
  }

  ...
  
  // add noises
  MPPIState curr_state(vt, wt, robot_pose_map.pose.position.x,
                       robot_pose_map.pose.position.y,
                       tf2::getYaw(robot_pose_map.pose.orientation));
  MPPISampledControlSequence sampled_control_seq;
  MPPISampledStateSequence sampled_state_seq;
  generateNoisedTrajectories(curr_state, prev_control_seq_, &sampled_control_seq,
                             &sampled_state_seq);
  // evaluate costs
  Eigen::ArrayXd costs;
  const auto& path_valid_flags = getPathValidFlags(prune_plan);
  MPPICostFeature cost_feature(
      control_dt_, &prune_plan, prune_path_length,
      getPathFurthestReachedPointIndex(prune_plan, sampled_state_seq),
      &path_valid_flags, costmap_ros_, mppi_config_.motion_constraints());
  if (cost_engine_ptr_->evaluate(mppi_config_.cost_terms(), cost_feature,
                                 sampled_state_seq, &costs)) {
    // extract optimal control
    const auto& curr_control_seq =
        updateControlSequence(costs, prev_control_seq_, sampled_control_seq);
    const auto& optimized_trajectory =
        extractOptimalTrajectory(curr_state, curr_control_seq);
    cmd_vel.linear.x = curr_control_seq.vx_seq(0);
    cmd_vel.angular.z = curr_control_seq.wz_seq(0);
    prev_control_seq_ = curr_control_seq;
  } else {
    cmd_vel.linear.x = 0.0;
    cmd_vel.angular.z = 0.0;
    R_WARN << "[MPPIController] Error occurs in cost engine.";
  }

  return true;
}

3.2 Python仿真

以下是核心代码

python 复制代码

def plan(self, path: List[Point3d]):
    """
    MPPI motion plan function.
    """
    for _ in range(self.params["max_iteration"]):
        # break until goal reached
        robot_pose = Point3d(self.robot.px, self.robot.py, self.robot.theta)
        if self.shouldRotateToGoal(robot_pose, self.goal):
            real_path = np.array(self.robot.history_pose)[:, 0:2]
            cost = np.sum(np.sqrt(np.sum(np.diff(real_path, axis=0) ** 2, axis=1, keepdims=True)))
            return True

        # calculate velocity command
        sampled_control_seq, sampled_state_seq = self.generateNoisedTrajectories(self.prev_control_seq_)
        critic_feature = CriticFeature(
            path=prune_path,
            local_path_length=local_path_length,
            furthest_reached_path_point_index=self.getPathFurthestReachedPoint(prune_path, sampled_state_seq),
            path_valid_flags=self.getPathValidFlags(prune_path),
            motion_constraint=self.motion_constraint,
        )
        cost_trajectories = self.cost_engine_.evalTrajectoriesScores(critic_feature, sampled_state_seq)
        curr_control_seq = self.updateControlSequence(
            cost_trajectories, self.prev_control_seq_, sampled_control_seq
        )
        optimized_trajectory = self.extractOptimalTrajectory(curr_control_seq)
        u = DiffCmd(curr_control_seq.vx_seq[0], curr_control_seq.wz_seq[0])
        self.prev_control_seq_ = curr_control_seq

        # feed into robotic kinematic
        self.robot.kinematic(u, dt)

    return False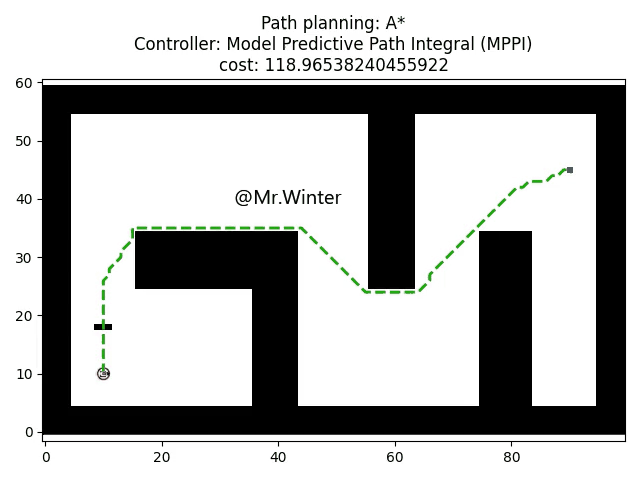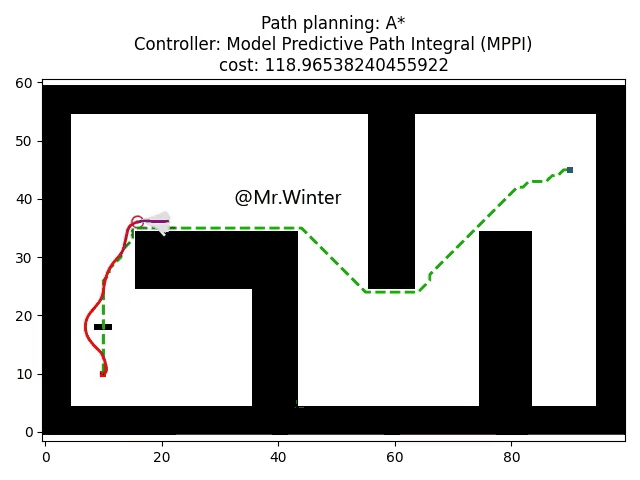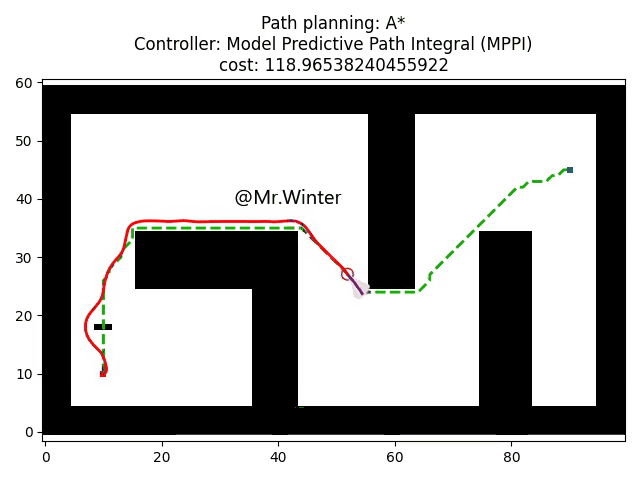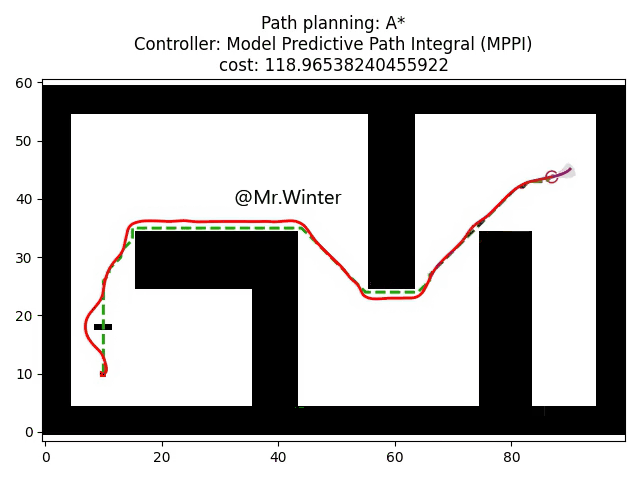

完整工程代码请联系下方博主名片获取

🔥 更多精彩专栏：

👇源码获取 · 技术交流 · 抱团学习 · 咨询分享请联系👇