摘要:摘要:针对电动汽车大规模接入和可再生能源不确定性带来的配电网运行挑战,本文提出一种电缆配电网多时段二阶段鲁棒优化方法。创新性地构建了计及OLTC、ESS、SVC等设备调控作用的多时段优化模型,采用快速求解算法降低计算复杂度。通过将非线性问题转化为线性规划,并利用Big-M方法处理不确定性变量,显著提高了求解效率。仿真结果表明,该方法能在2次迭代内收敛,计算时间缩短90%以上,有效保证了配电网在最恶劣场景下的安全经济运行。与传统CCG算法相比,在保证优化精度的同时大幅提升了计算性能。
1 研究背景
(1)配电网面临的新挑战:
- 电动汽车(EV)大规模接入,无序充电导致负荷峰谷差增大;
- 可再生能源(风电、光伏等分布式电源,DG)具有强不确定性,影响配电网的实时功率平衡和电压稳定;
- 城市配电网中广泛使用电缆线路,其对地分布电容电流较大,传统配电网潮流模型不适用。
(2)现有研究存在的不足:
- 现有鲁棒优化方法(如列与约束生成算法,CCG)在求解多时段问题时计算复杂度高,难以满足实时调度需求;
- 多数研究未同时考虑电缆对地电容、调节设备动作代价、以及分布式电源的有功与无功协同调节能力。
- 传统配电网模型未充分适应电缆线路的特性,容易导致电压越限或电流越限问题。
2 创新点
- 计及OLTC、SCR、ESS、SVC和DG的有功、无功调控作用,并将单时段最优潮流模型扩展至多时段情形;
- 计及负荷、风电出力的不确定性,构建电缆配电网多时段二阶段鲁棒优化模型;
- 提出一种快速求解方法,求解第一阶段模型时无需增加优化变量和约束条件,求解第二阶段多时段模型时只需针对每个阶段进行求解,极大降低求解复杂度,提高求解速度。
3 采用放射状运行结构的电缆配电网多时段有功与无功协调确定性优化模型
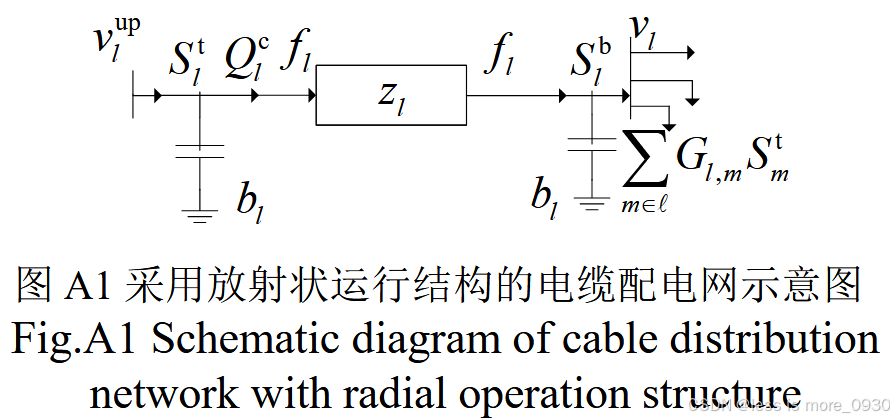
两阶段优化方法:
第一阶段变量ψt(离散变量,不能频繁动作,在各优化时段确定后,出现不确定性也不能改变):ESS充放电功率和存储电量、OLTC分接头位置、SCR投入组数以及其他离散变量。
第二阶段变量φt(连续变量,不确定性出现后可实时调整):支路功率、支路电流、电压幅值平方及其上下限变量、DG有功和无功、SVC无功、SCR无功等。
电缆配电网多时段最优潮流确定性优化模型:
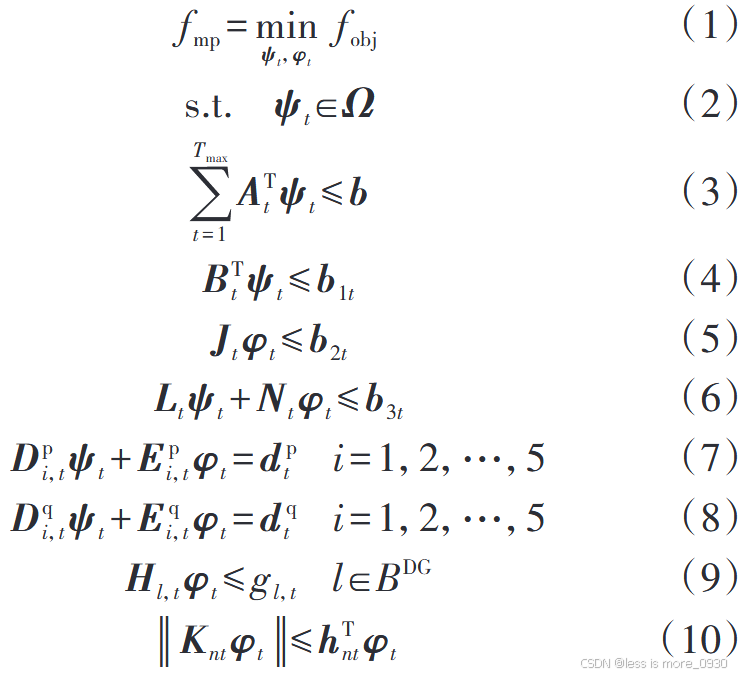
各表达式含义:
1、式(1):优化时段(24h)内的总运行费用最小。

式中,fmp 为主问题的目标函数,fobj为总运行费用。
目标函数由配电网运营商购电费用、ESS、OLTC与SCR的运行费用组成:
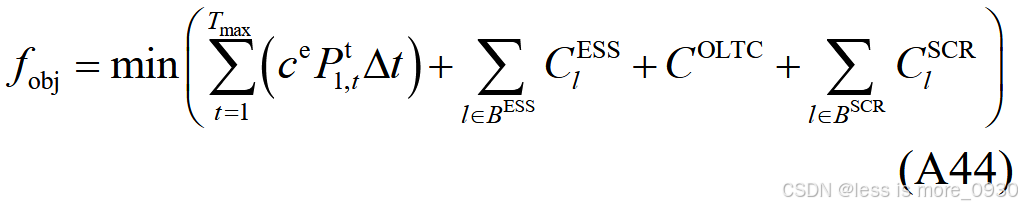
式中,c e为购电电价;P t 1,t 为t 时段根节点有功功率;∆t 、T max分别为优化调度的时间间隔与总时段数;C ESS l 为储能运行成本;C OLTC l 为有载调压变压器运行成本;C SCR l 为可投切电容电抗器运行成本;B ESS、BSCR分别为ESS、SCR接入节点集。
2、式(2):表示第一阶段变量的取值范围,对应于ESS的充放电功率上限、荷电状态上下限、SCR的投入组数、OLTC的档位上下限约束等。

式中,ψt 为第一阶段变量矩阵;Ω为第一阶段变量的取值集合。
3、式(3):表示第一阶段变量在不同时段的耦合关系,对应于优化调度周期内SCR与OLTC的动作次数、ESS相邻时段的荷电量关系、循环次数约束等。

4、式(4):表示每个时段第一阶段变量的线性不等式约束,对应于ESS充放电功率、状态之间关系的约束等。

5、式(5):表示每个时段第二阶段变量的线性不等式约束。

对应于附录A式(A3)、(A6)、(A12)、(A13)、(A16)---(A19)、(A38)、(A41)等:
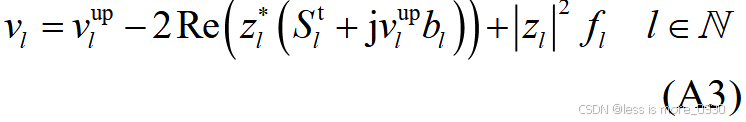
式中,vl 、fl 为电压、电流有效值的平方;v up l 为节点l 父节点电压有效值的平方;Re为取实部运算符;zl 、bl 分别为支路l 的阻抗、电纳;S t l为支路首端复功率;
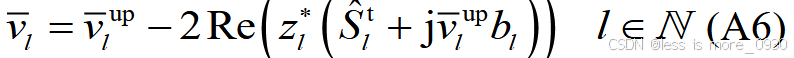
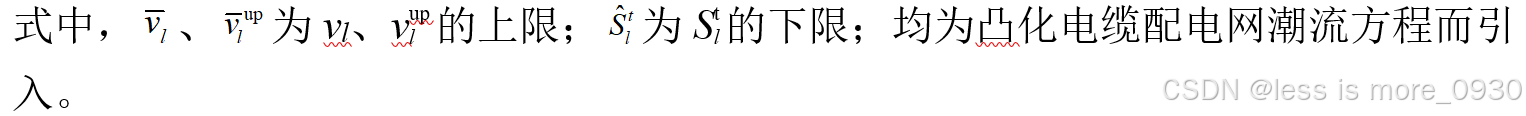
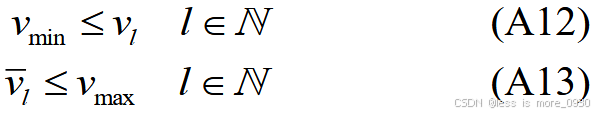
式中,v max、vmin分别为节点电压有效值上、下限的平方。
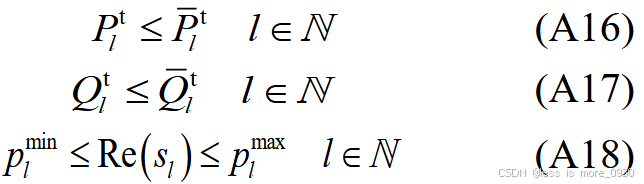
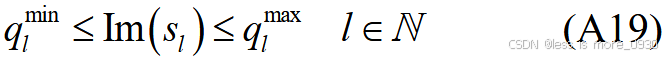
式中,pl max、pl min分别为节点l 吸收有功的上、下限;ql max、ql min分别为节点l吸收无功的上、下限。
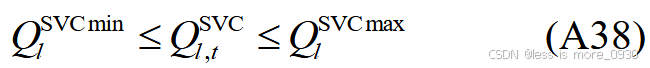
式中,Q SVCmax l 、Q SVCmin l分别为SVC注入无功的上、下限。
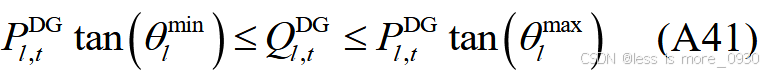
式中,θ min l 、θ max l分别为DG功率因数角上、下限。
6、式(6):表示每个时段第一、二阶段变量的耦合关系,对应于包含OLTC支路的电压降落方程等。

7、式(7)、式(8):分别表示每个节点的有功、无功平衡方程。
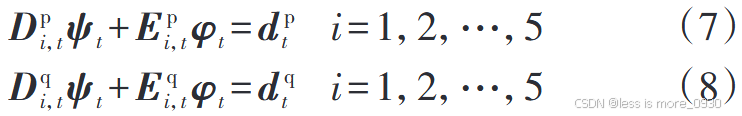
对应于附录A式(A2)、(A5)、(A7)、(A10)、(A11)等:
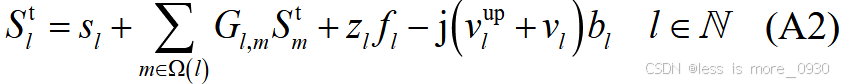
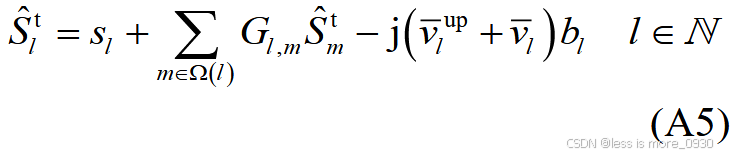
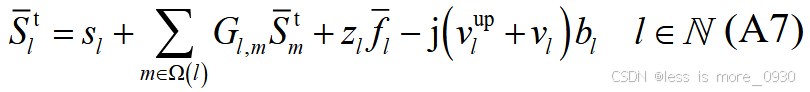
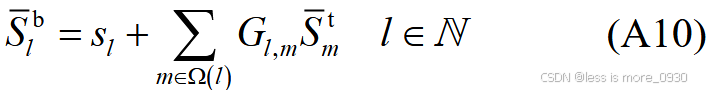
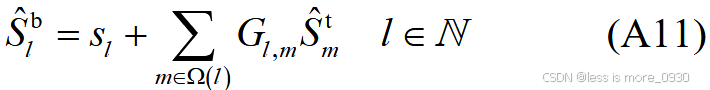
8、式(9):表示DG有功约束。
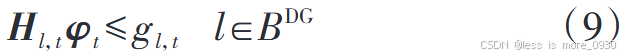
式中,gl ,t 为t 时段节点l的DG预测有功。
对应于附录A式(A42)等。

9、式(10):表示二阶锥约束。

对应于附录A式(A29)、(A30)、(A35)、(A36)、(A43)等。
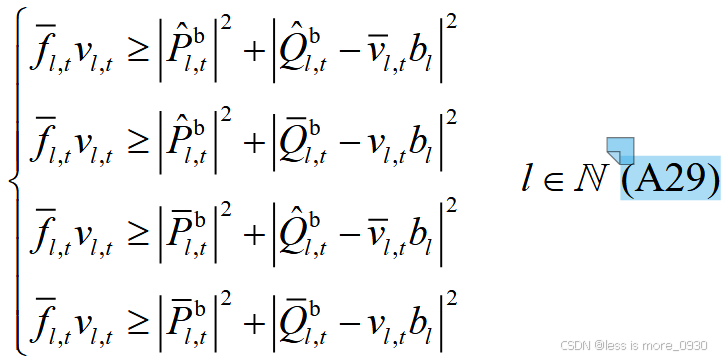
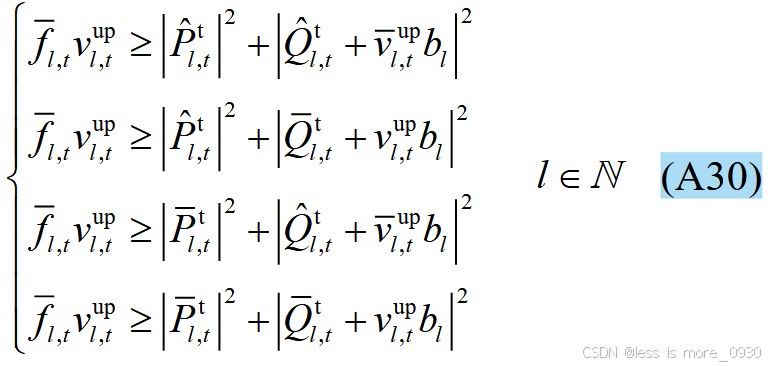
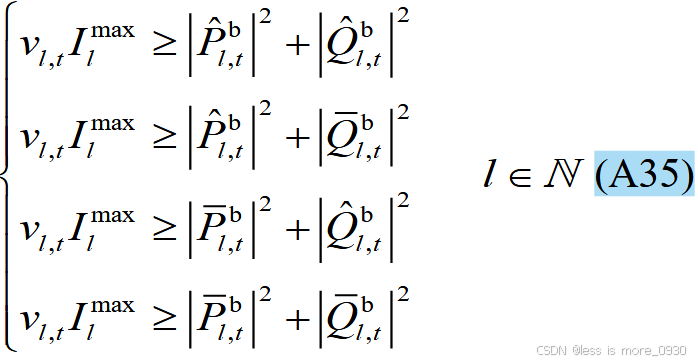
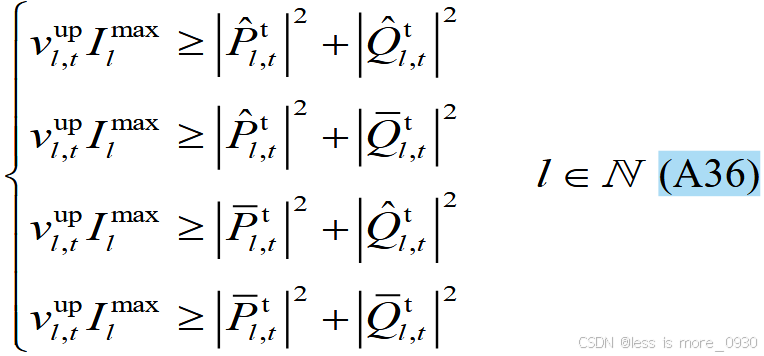
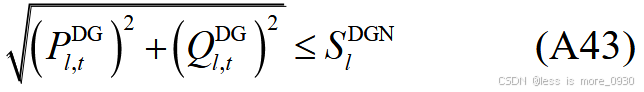
4 鲁棒优化模型
由于光伏、风电、负荷具有较强的不确定性,若采用确定性优化模型,则难以保证配电网安全运行,因此,采用鲁棒优化模型(外层第一阶段决策变量ψt 用于将最恶劣场景下的配电网总运行费用降至最低,内层最大-最小双层优化模型决策变量φt用于找出最恶劣场景):
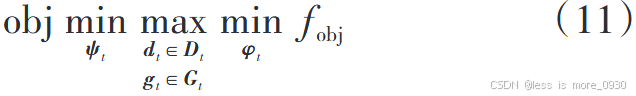
式中,Dt 、Gt 分别是t时段负荷功率、DG有功出力的不确定性集。
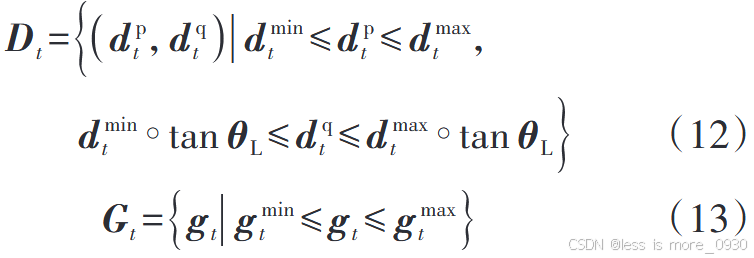
式中,"∘"表示按分量点乘;θ L为预测的负荷功率因数角向量;g t 为t 时段所有DG有功出力向量;d max t 、d min t 和g max t 、g min t 分别为t 时段负荷功率和DG有功出力上、下限,可由区间预测得到。

5 求解方法
二阶段鲁棒优化主问题:
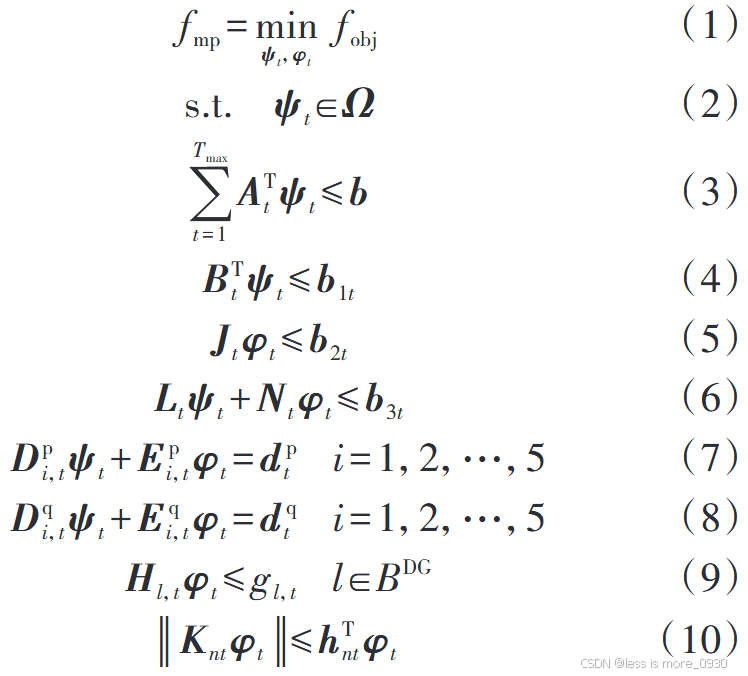
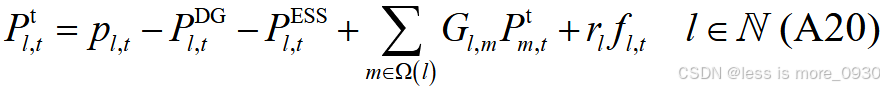
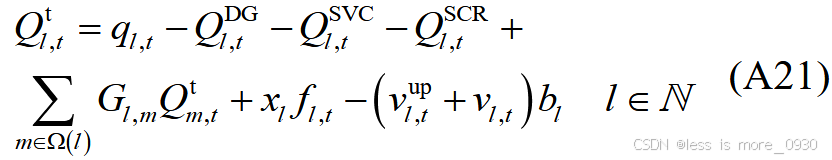

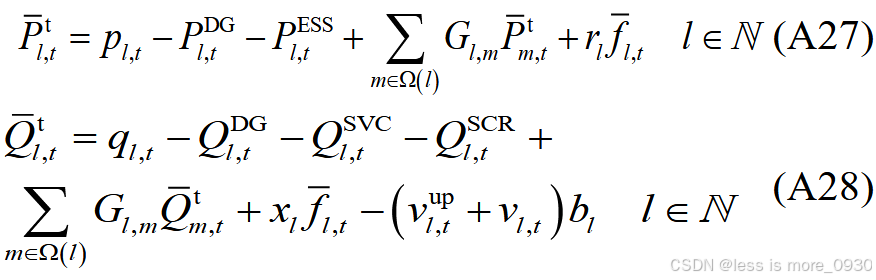
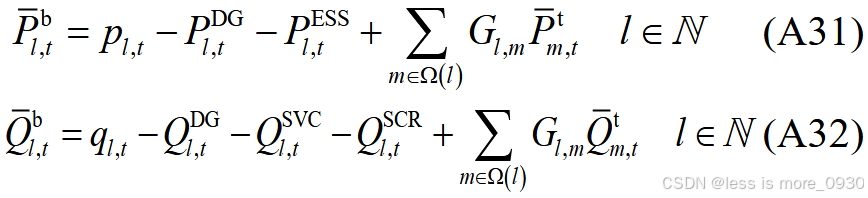
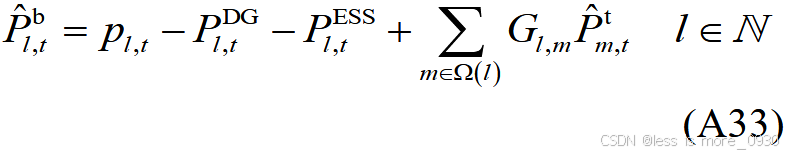
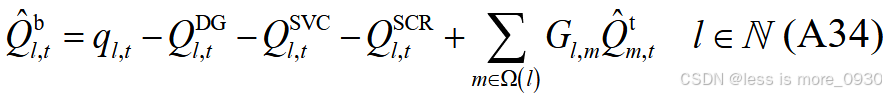
将求解主问题得到的第一阶段变量优化结果代入式(A20)、(A21)、(A24)、(A25)、(A27)、(A28)、(A31)---(A34)中,构建二阶段鲁棒优化次问题:
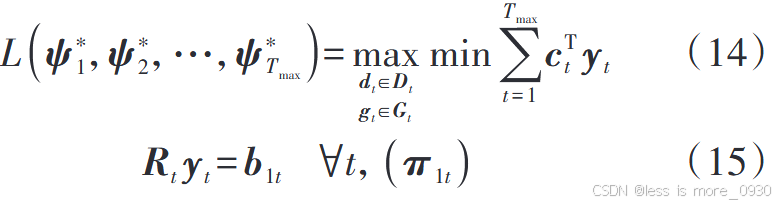
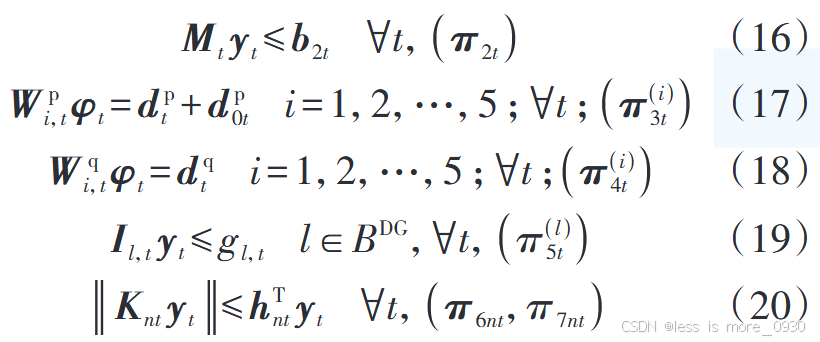
各表达式含义:
1、式(14):次问题的目标函数
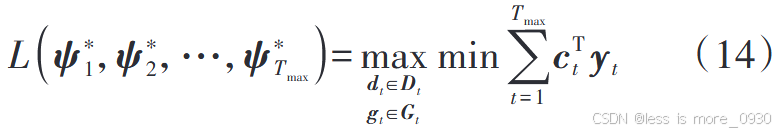
式中,ψt *(t =1,2,...,T max)为t时段第一阶段变量最优值。
2、式(15):表示第二阶段变量等式约束,变量包括与SCR无功相关的虚拟变量等。
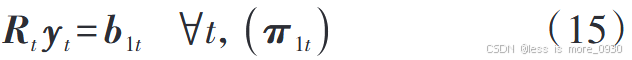
3、式(16):表示第二阶段变量不等式约束,如SVC无功、节点电压、支路电流上下限约束等。
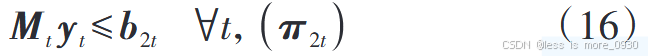
4、式(17)、(18):表示节点有功、无功潮流方程。
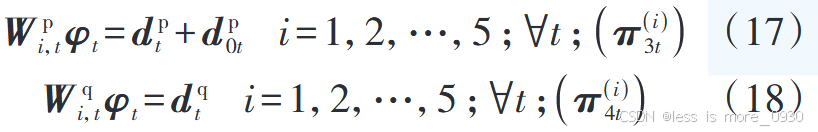
5、式(19):表示DG有功出力调度值小于或等于其预测值约束。
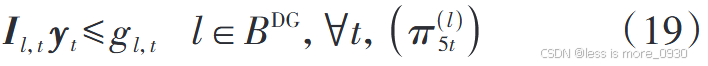
6、式(20):表示支路潮流二阶锥凸松弛不等式约束以及DG有功、无功与逆变器容量关系的二阶锥约束。
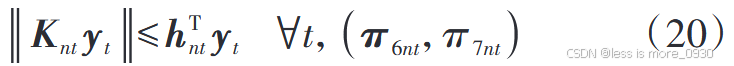
配电网运行成本最小化是一个线性问题,根据强对偶理论和第二阶段最小化问题中各约束对应的对偶变量可将其转化为max问题,并将两个max问题合并,将式(14)---(20)的最大-最小双层优化次问题简化为式(21)---(27)所示单层优化问题:
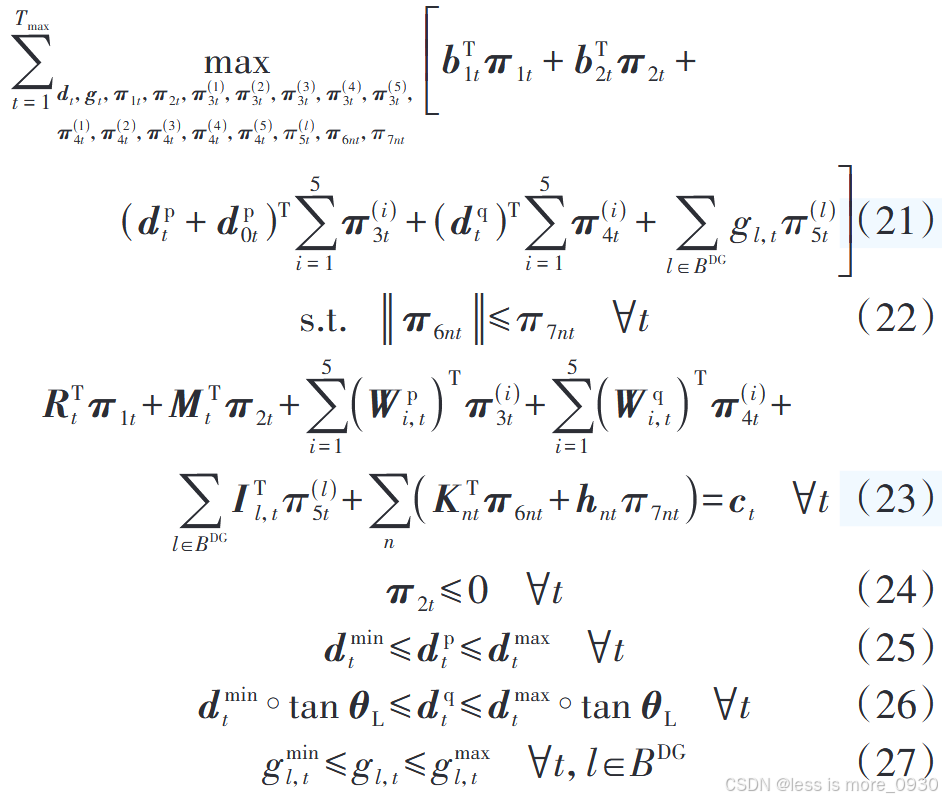
5.1 对偶问题推导过程
原问题为:
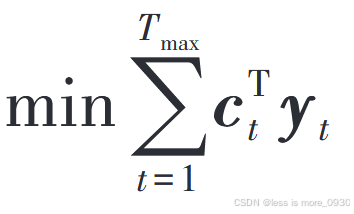
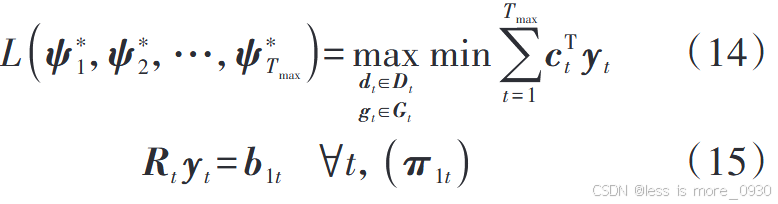
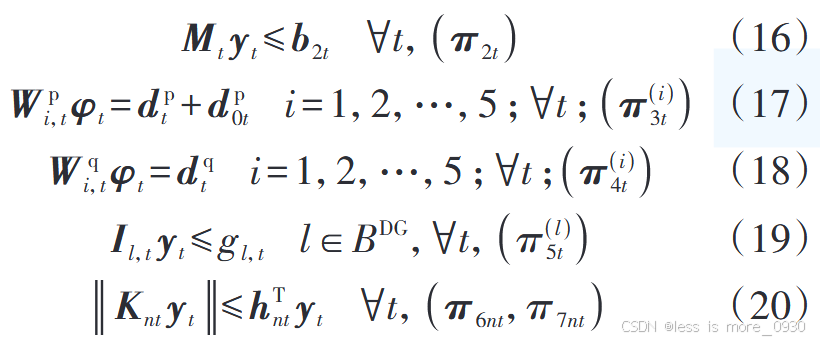
可以得到拉格朗日函数为:
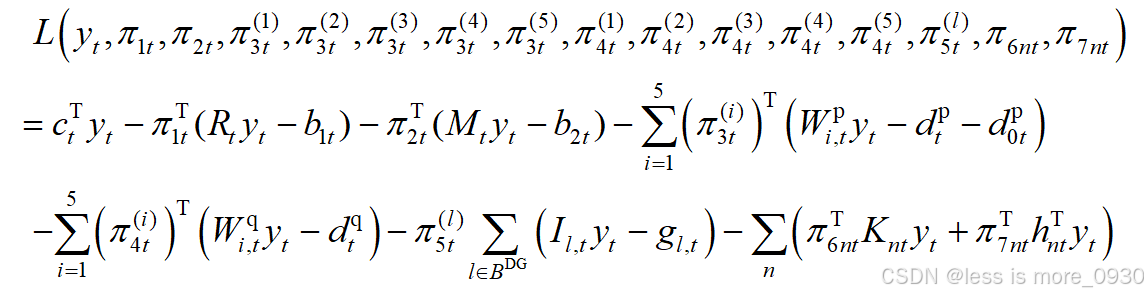
则拉格朗日对偶函数为:
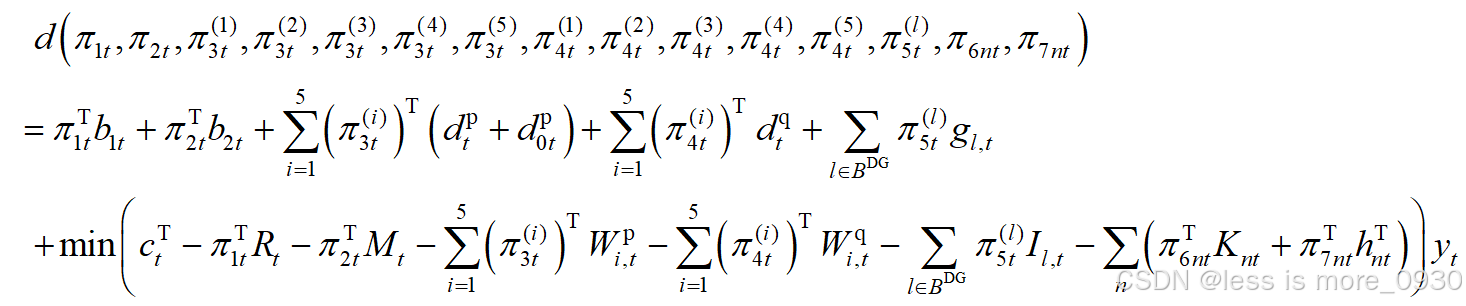
可得对偶问题的目标函数为:
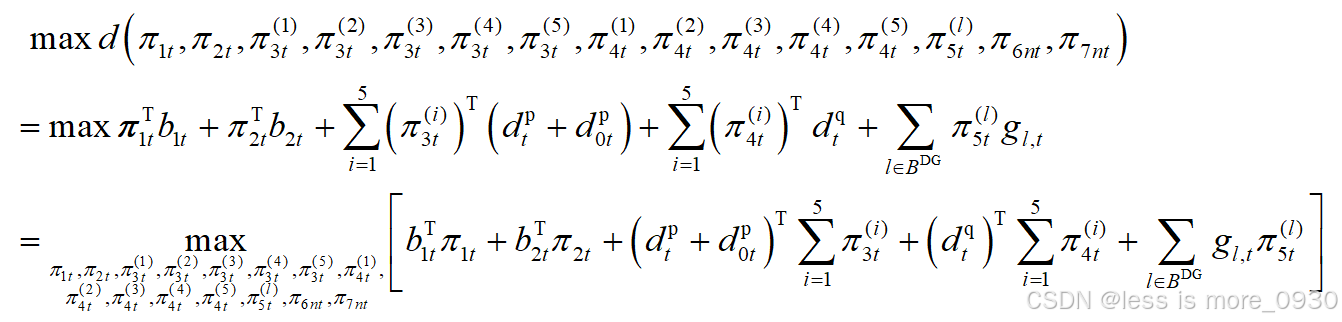
将两个 max 交换(最大化合并):
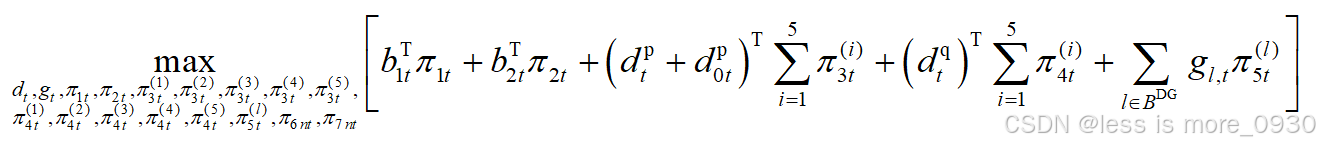
此时约束条件为:
(1)线性不等式约束引入的约束,为了得到有意义的对偶函数,必须使其小于0。
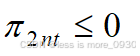
(2)二阶锥约束的对偶变量必须满足的锥可行性条件。
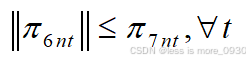
(3)这是拉格朗日对偶理论的核心步骤:内层最小化问题转化为对偶最大化问题时,要求拉格朗日函数关于原变量yt的梯度为0,线性形式决定此处梯度为0与系数为0是一码事。
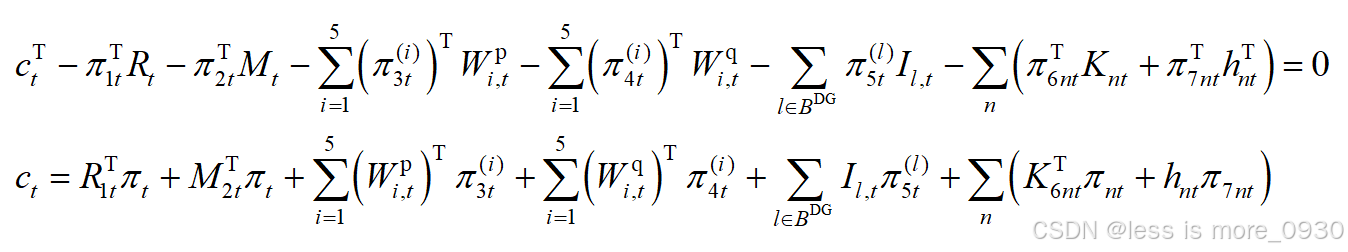
(4)不确定性集约束
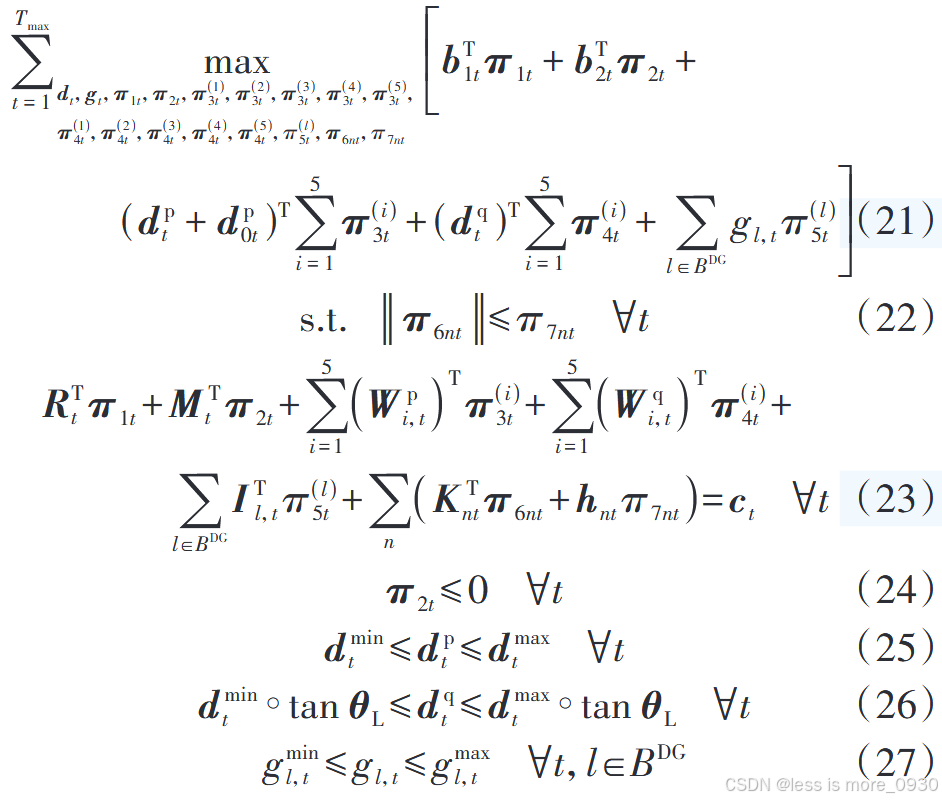
不确定性集中各分量相互独立,只有当负荷、间歇性DG出力在不确定性集表征的多面体顶点取值时,才能产生最恶劣场景。因此寻找最恶劣场景时,只需要检查所有顶点即可,而不必搜索内部点。单层优化子问题中,存在不确定性变量与对偶变量的乘积,出现非线性项,利用big-M方法对其进行线性化。
5.2 Big-M方法线性化原理
Big-M方法适用于处理形如:
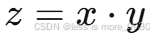
其中,x 是连续变量,y 是0-1变量或有界变量,z为辅助变量。
基本思路:
- 引入辅助变量z =x ∙y;
- 引入0-1变量δ 表示y处于上界或下界;
- 通过约束条件将z 与x 、y的关系线性化。
5.3 具体线性化步骤
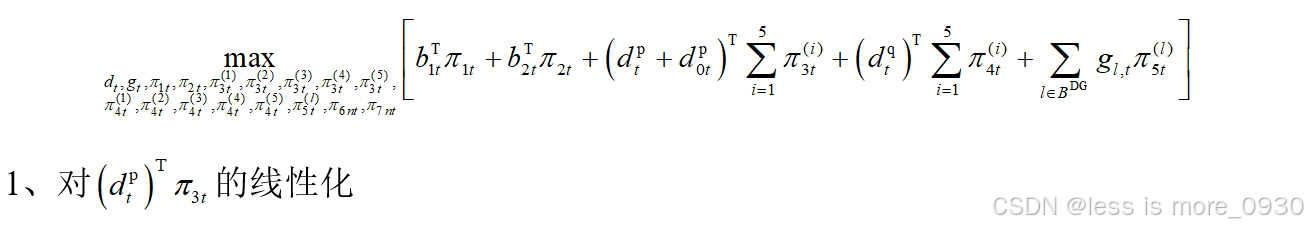
不确定性变量dtp的取值范围为:
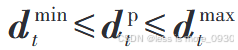
引入辅助变量:

其中,δt ,n为0-1变量。
则(δt ,n取0和1时分别表示不确定变量取到最小值和最大值):
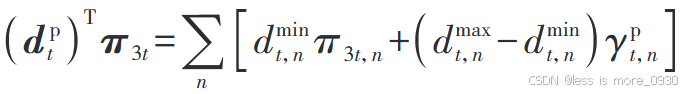
约束条件为(目标是:在不使用非线性乘积γ =δ *π 的情况下,仅用线性约束来强制实现δ =0时,γ =0;δ =1时,γ =π 3t ,n 这一逻辑,两组约束分别对δ =0和δ=1的情况进行约束,缺一不可):
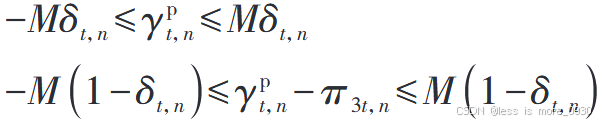
此处M 为一个足够大的正数,保证δ =0时,γ =0;δ =1时,γ =π 3t ,n。
因此,将三个非线性项进行线性化的结果如下:
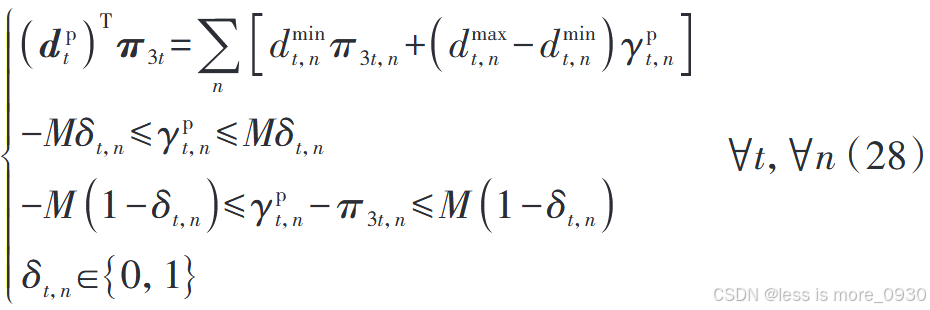
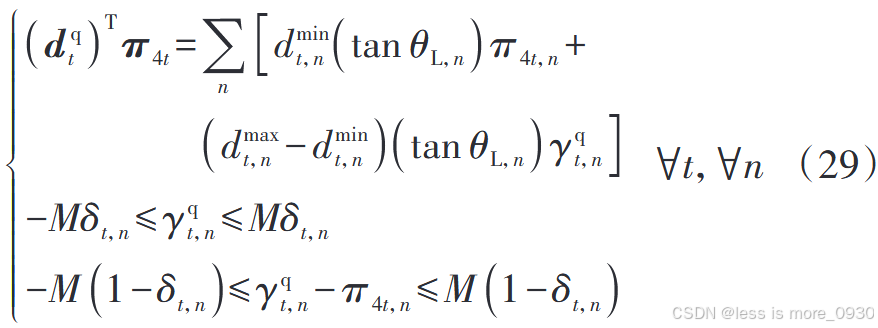
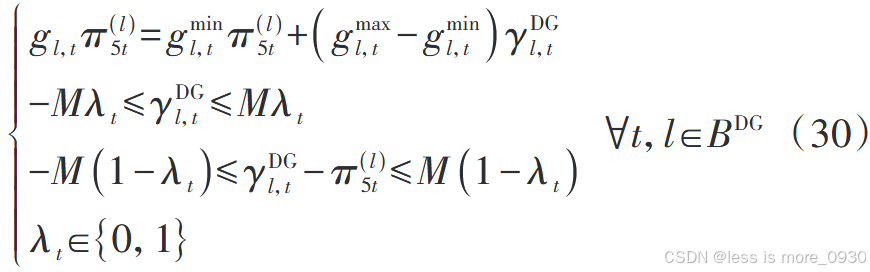
6 求解方法
6.1 新老方法对比
1、传统CCG算法
(1)场景保留与传递
- 当不确定性集非凸时,如果只保留当前场景而丢弃历史场景,可能导致算法无法收敛到最优解,甚至陷入循环。因此需要保留所有场景来保证CCG算法的收敛性,但代价是主问题规模线性增长。
- 每次迭代求解次问题后,都会得到一个当前最恶劣场景(比如某时段负荷最大、风电出力最小)。
- 所有历史最恶劣场景都会被保留,并一起传递给下一次迭代的主问题。
(2)主问题规模的膨胀
- 为了应对这些历史场景,主问题必须为每一个历史场景复制一套对应的第二阶段决策变量和约束条件。
例如:
第1次迭代:主问题包含1个场景的变量和约束。
第5次迭代:主问题包含5套场景的变量和约束。
- 每迭代一次,主问题规模就扩大一次(新增变量和约束)。
2、本文方法
(1)关键观察:不确定性集是凸集
- 在实际配电网中,负荷、风电、光伏的不确定性集合通常是一个凸集(如区间、多面体)。
- 对于凸不确定性集,最恶劣场景通常位于集合的极值点(顶点)。
(2)本文的核心简化逻辑
- 在迭代过程中,当前找到的最恶劣场景,其恶劣程度≥之前所有场景。
因此,主问题只需要针对当前最恶劣场景进行优化,就自动覆盖了所有历史场景的约束要求。
6.2 求解步骤

7 仿真结果
1、4节点配电网
在2---3h,电价最低,ESS以最大功率充电;在20---21h,电价最高,ESS以最大功率放电。
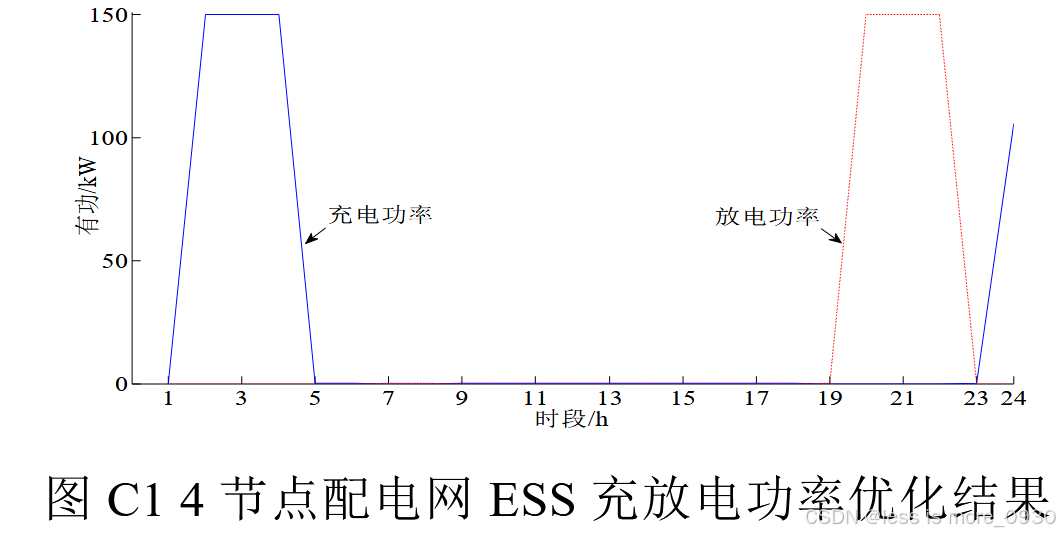
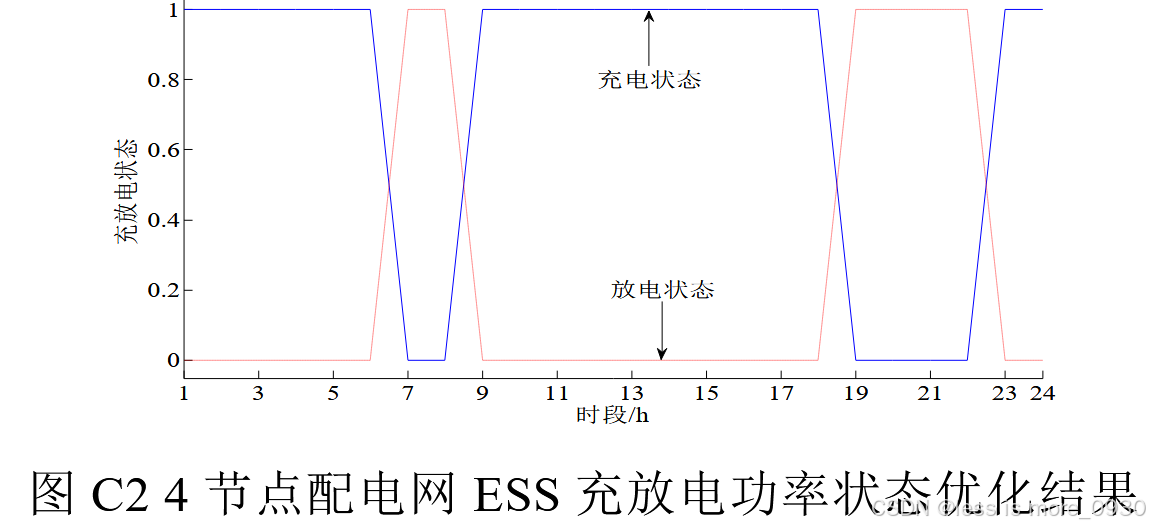
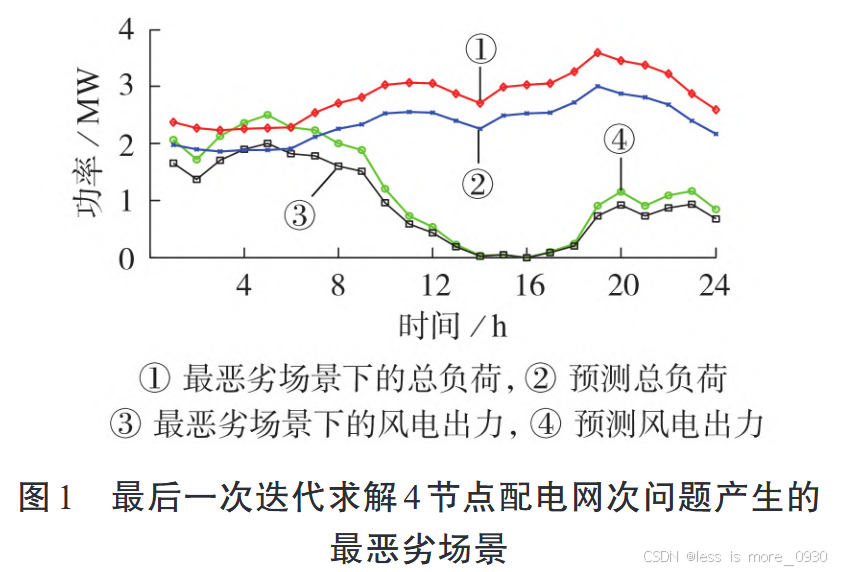
体现了鲁棒优化中常见的"负荷最高、可再生能源出力最低"的保守假设,即系统在最不利情况下仍能安全运行。数据来源于最后一次迭代求解次问题,说明算法已收敛,得到的最恶劣场景是稳定的。
PMSG与SVC注入无功恒为负值,这是因为电缆线路较长(容升作用明显),PMSG容量较大(为了输送功率,需要并网点维持更高电压),电缆对地分布电容注入无功与风电有功出力较大,PMSG与SVC必须吸收无功才能保证电压处于额定范围内。此外,当PMSG有功出力最大(小)时,变流器吸收的无功最大(小),这是因为PMSG功率因数角设置为[-π/4,π/4],而且当PMSG变流器吸收的无功较大(小)时,SVC吸收的无功较小(大),通过SVC与PMSG变流器的相互配合可调节配电网电压并降低网损。
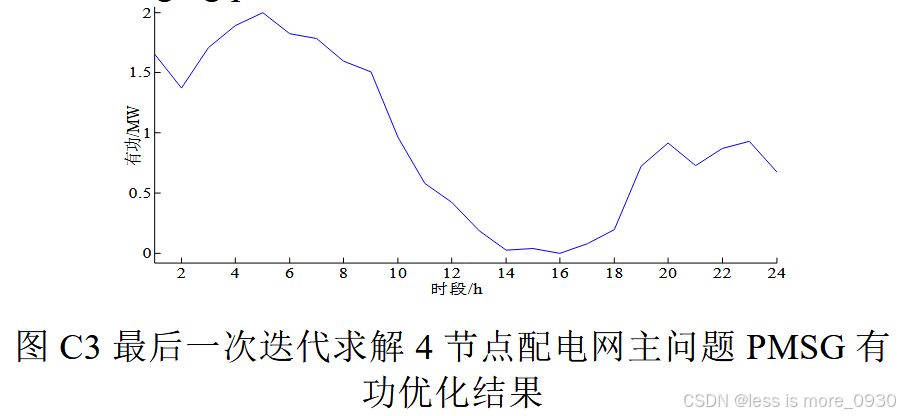
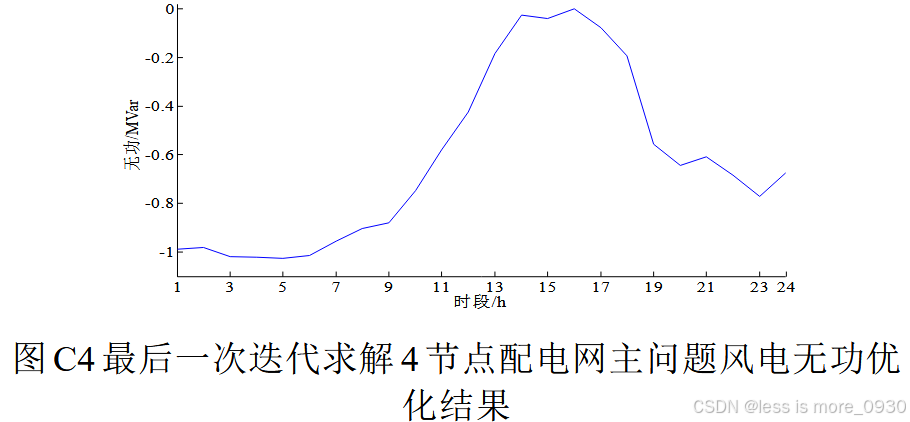
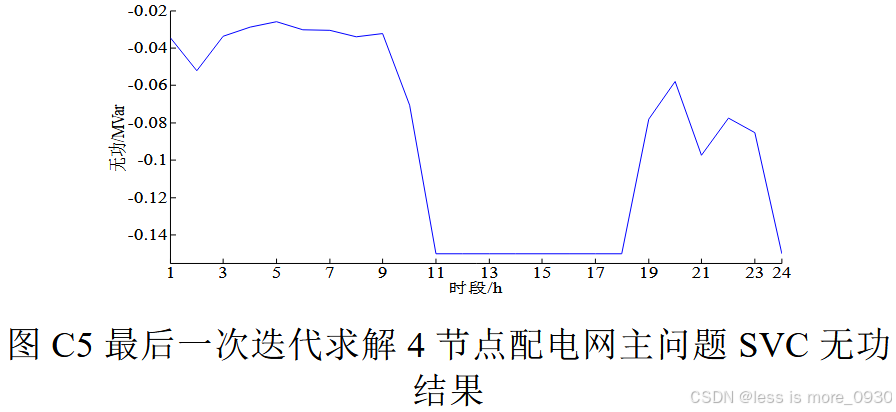
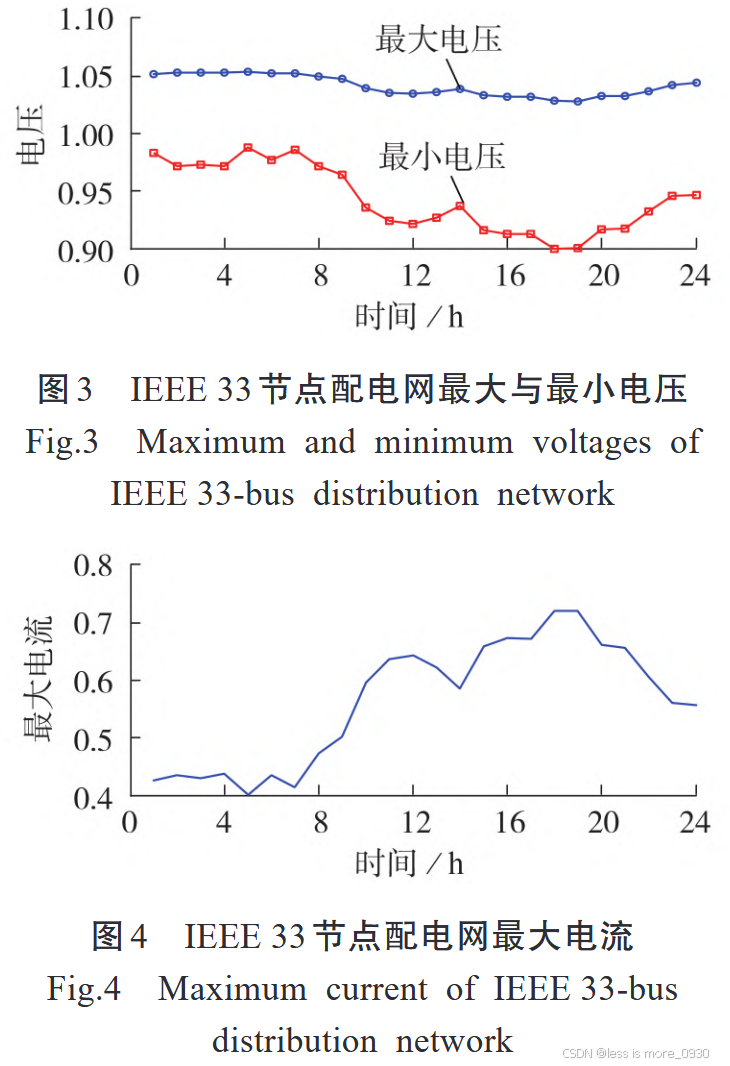
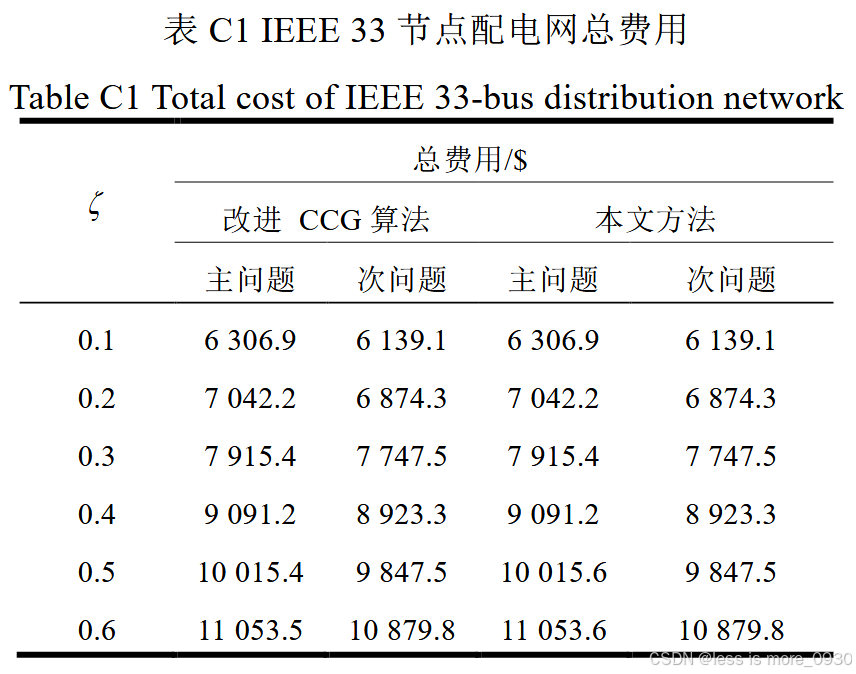
2、IEEE33节点配电网
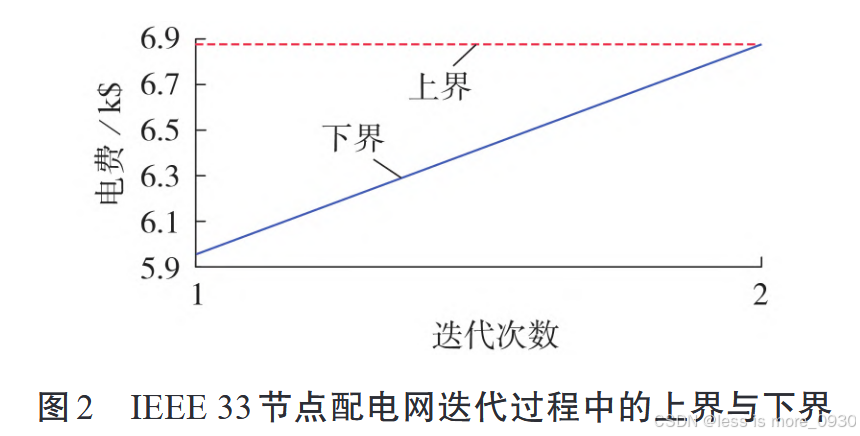
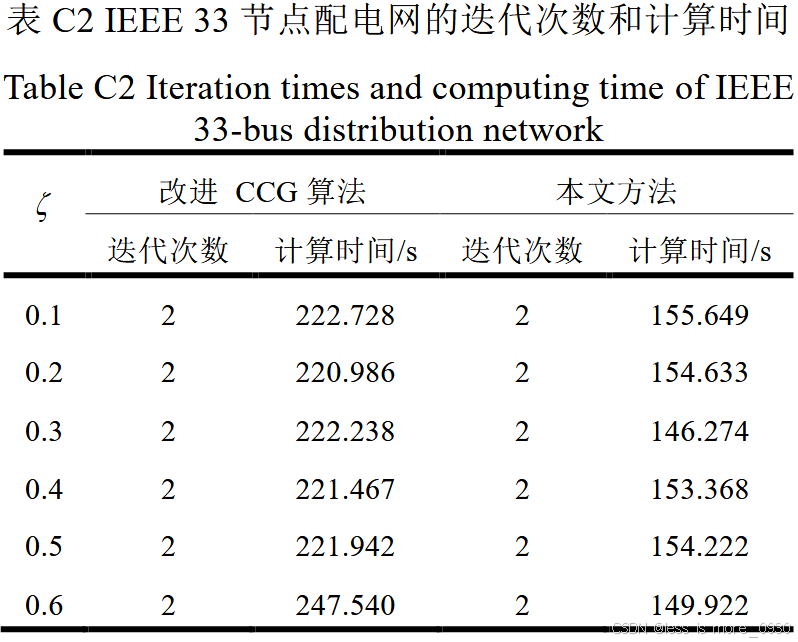
在迭代过程中,上界保持不变,下界增大,当上界与下界的相对对偶间隙小于给定容差时,程序终止运行;采用本文方法只需迭代2次即可收敛。
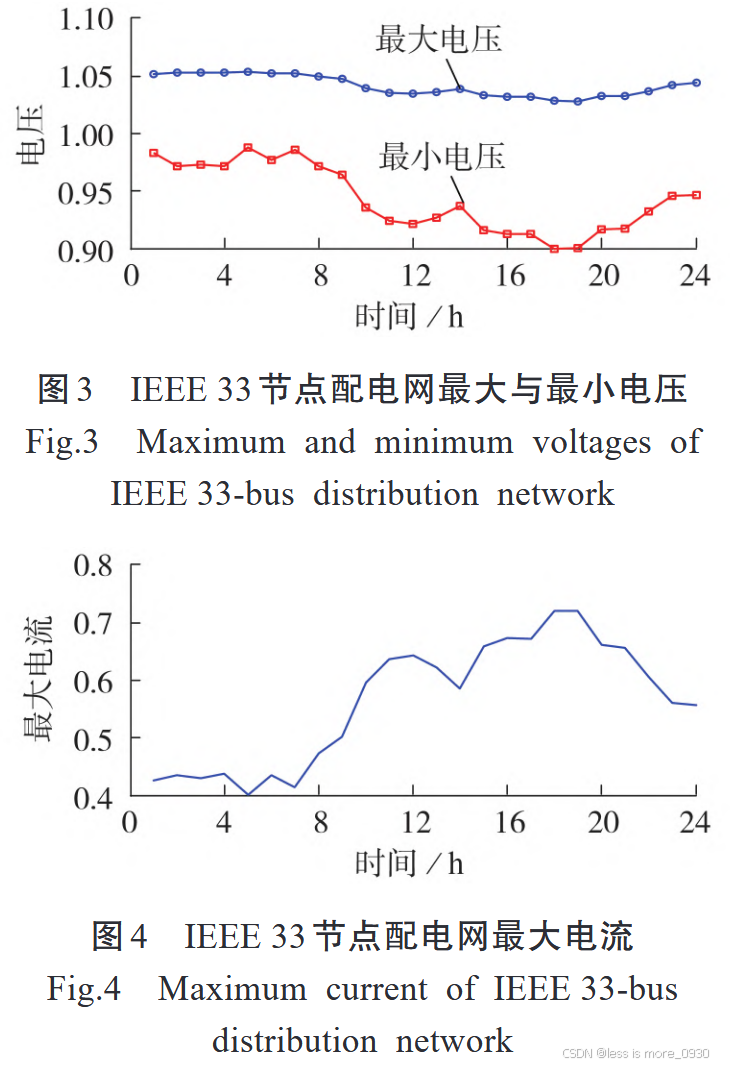
最大和最小电压以及最大电流均处于额定范围内。
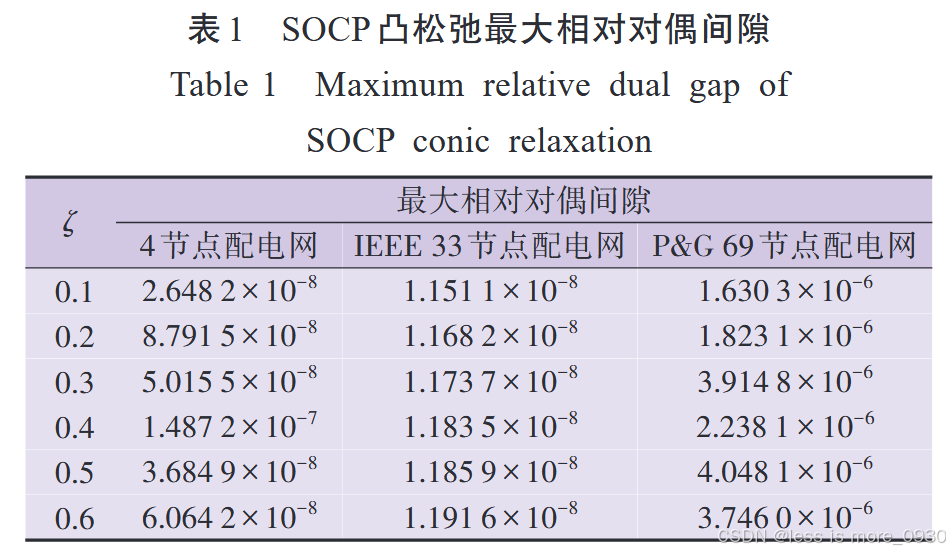
3个配电网的最大相对对偶间隙均小于5×10-6,因此,凸松弛的精度足够高,SOCP与原始非凸模型是等价的,优化结果即为原始非凸模型的最优解。
3、与CCG算法比较
在不同的预测误差下,采用2种方法得到的总费用一致。
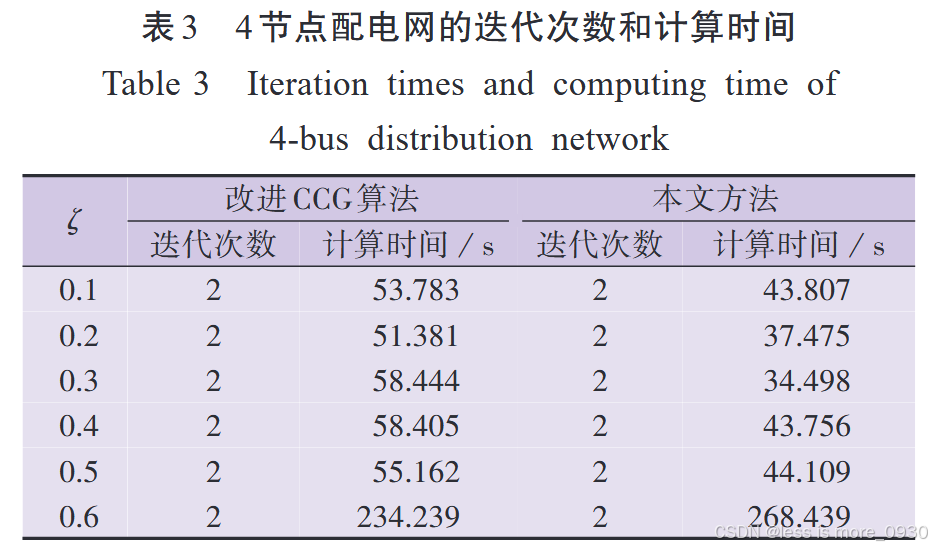
除了在4节点配电网中预测误差为0.6时本文方法的计算时间长于改进CCG算法外,在其他场景下,本文方法的计算时间均短于改进CCG算法。
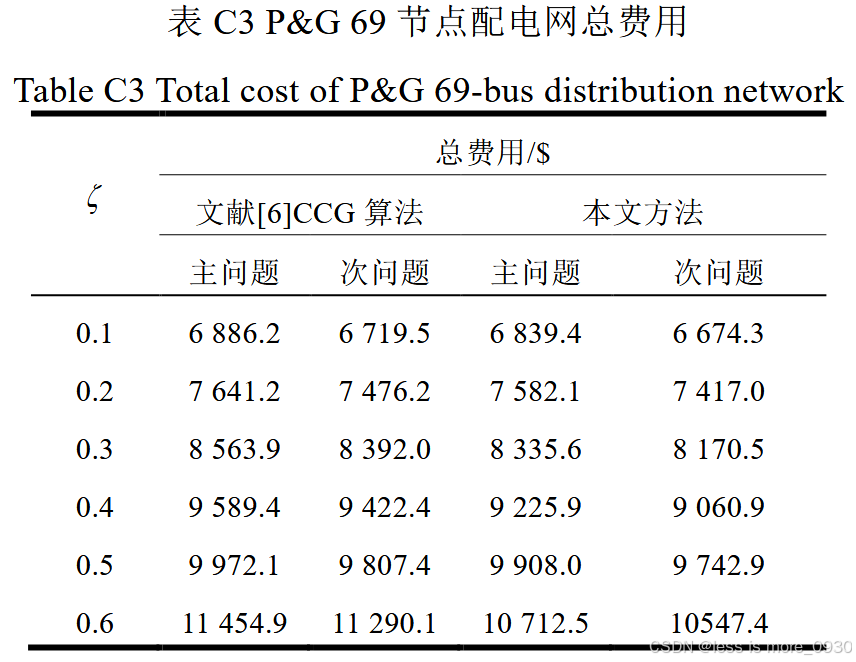
总费用随着预测误差的增大而增加,即在最恶劣场景下配电网的运行费用随着负荷与间歇性DG出力不确定性的增大而增加,优化计算结果与实际情况相符。
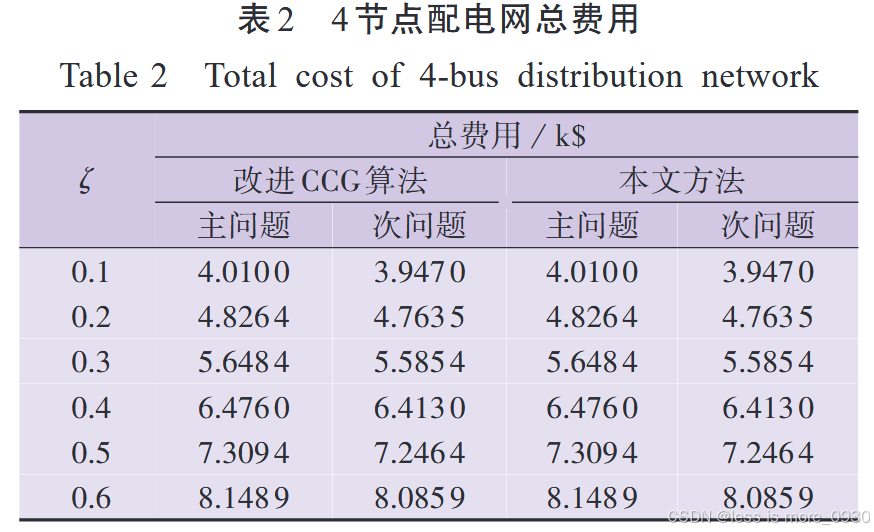
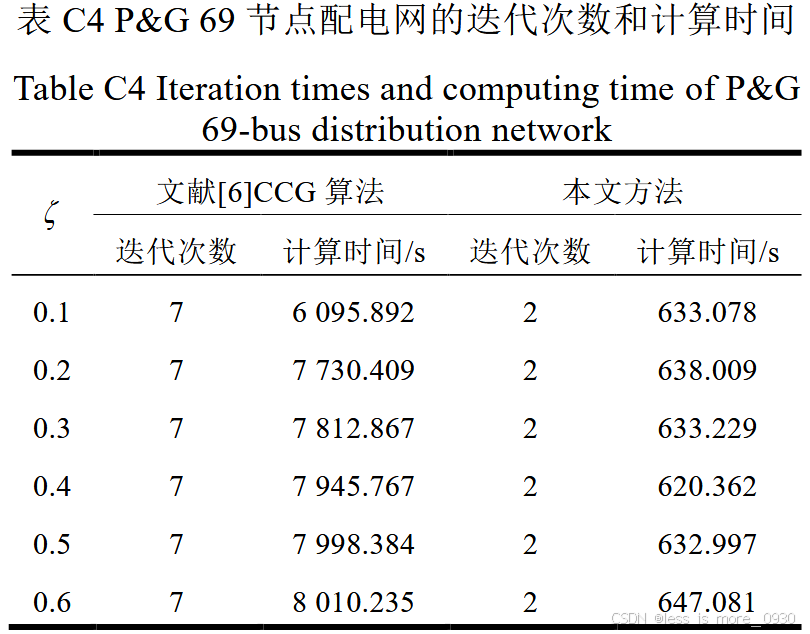
不同的预测误差下,采用本文方法求解主、次问题得到的总费用均小于文献[6] CCG算法。
相同的相对对偶间隙,文献[6]CCG算法优化结果的精度低于本文方法。
文献[6]CCG算法需迭代7次耗费6095~8010s才终止运行,而本文方法迭代2次就终止运行,耗费时间短于650s。
本文方法所需的内存远小于文献[6]CCG算法。
参考文献
1\]张剑,崔明建,何怡刚.计及分时电价的电缆配电网多时段二阶段有功与无功协调快速鲁棒优化调度方法\[J\].电力自动化设备,2023,43(06):94-100.DOI:10.16081/j.epae.202211014.