基于 GPU 并行加速的 pRRTC 算法：赋能 Franka 机械臂的高效、稳定运动规划

高自由度机械臂（如7 自由度的 Franka Research 3）在执行复杂任务时，运动规划的实时性和一致性是至关重要的。传统的基于采样的运动规划算法（SBMP），如 RRT-Connect，虽然在处理高维空间问题上表现出色，但在复杂受限环境下的计算开销依然巨大。

为了攻克这一难题，科研团队推出了 pRRTC------一种专为 GPU 并行计算协同设计的 RRT-Connect 变体算法。该算法通过多级并行化策略，在 Franka 等机器人平台上实现了亚毫秒级的规划速度和极高的稳定性。

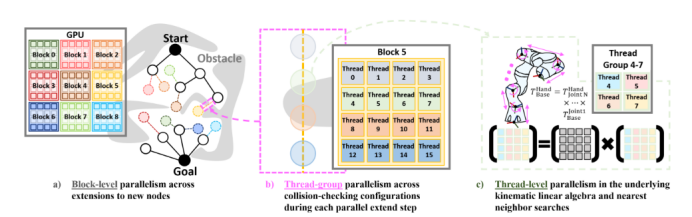
图1：pRRTC在GPU上的三级并行架构示意图

pRRTC的核心技术框架

pRRTC的核心优势在于其对GPU架构的深度挖掘，将并行化从简单的碰撞检测扩展到了算法的全流程。

多级并行机制：

中级（Mid-level）并行：pRRTC在GPU上异步运行数百个独立的RRT-Connect 迭代分支。这些分支同时对起始树和目标树进行探索，大幅提升了在配置空间（C-space）中的搜索效率。
低级（Low-level）算子并行：算法对最近邻（NN）搜索和离散化边线的碰撞检测（CC）进行了并行化处理。

SIMT优化的碰撞检测： 碰撞检测通常是运动规划的性能瓶颈。pRRTC引入了单指令多线程（SIMT）优化技术：

**高效内存管理：**为了支持高自由度机器人（如Franka的7 DoF或Franka双臂14 DoF），pRRTC优化了GPU块与线程间的内存分配，通过覆盖中间结果减少了高达 7 倍的显存占用，从而支持更多并发规划任务。

针对Franka机械臂的实验表现

研究团队利用MotionBenchMaker 数据集对FR3进行了严格测试。测试场景涵盖了柜台操作、货架存取及受限空间抓取等多种复杂环境。

图2：MotionBenchMaker中的多样化Franka机器人实验场景

在MotionBenchMaker数据集的评估中，Franka Research 3展现了 pRRTC的卓越性能。

极速规划**：**在Franka机器人的7自由度场景下，pRRTC达到了亚毫秒级的平均规划时间。

高度一致性**：**相比于目前的尖端算法，pRRTC的规划时间标准差降低了5.4 倍。这意味着在不同复杂度的环境下，它都能提供稳定的响应时间，这对于实时控制系统至关重要。

路径成本优化**：**pRRTC生成的初始路径成本（Arc-length）平均降低了1.4倍。这是因为大规模并行采样使得算法更有可能在极短时间内发现更直接、更短的避障路径。

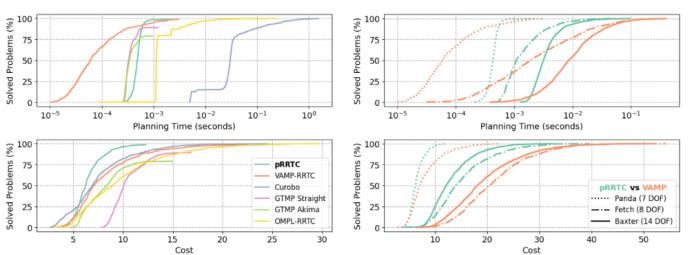
图3：Franka Panda机器人的规划时间与成本累积分布函数图

Franka双臂部署

为了测试pRRTC在真实场景下的表现，研究者将其部署在一套包含两台Franka Research 3机械臂（共14自由度）的实验平台上。

图 4 ：pRRTC在 Franka组合双臂 14自由度系统上的实时避障演示

**实时重规划（****Replanning）：**系统集成了Intel Realsense相机，通过Nvblox库将实时采集的深度图转化为欧几里德符号距离场（ESDF）。

**端到端频率：**在面对如"移动的泡沫棒"等动态障碍物时，pRRTC能够以 7.7 Hz 的端到端频率进行实时重规划。机械臂在运动过程中能够流畅地感知并规避障碍，展示了极高的实时响应能力。

消融研究：是什么让它如此强大？

通过在Franka组合双臂14自由度系统上的消融实验，研究者揭示了各项设计对性能的贡献：

**并行路径验证：**带来了9.4倍的加速，是贡献最大的单一优化。

**GPU优化FK内核：**提供了3.3倍的加速。

**四线程组设计：**带来了1.8倍的提升。

**并发****Block数量：**研究发现，当并发Block数量增加到256个时，系统性能达到饱和状态，展现了硬件利用率的最优平衡点。

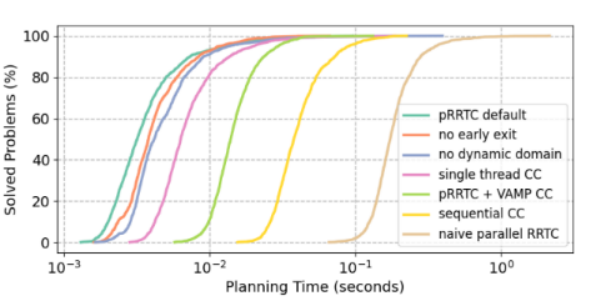
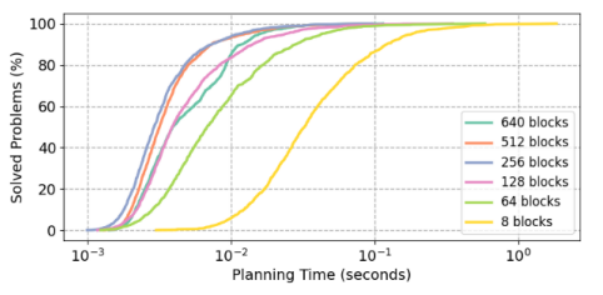
图5 & 6：pRRTC的设计消融实验与

结论

pRRTC算法通过深度融合GPU的并行计算特性，为Franka Research 3等高性能机械臂提供了一套低延迟、高一致性的运动规划解决方案。它不仅在理论性能上大幅超越了传统的CPU规划器，更通过实机部署验证了其在动态、复杂环境下的实用价值。